NP-полнота. Машина Тьюринга

1.

• https://old.mccme.ru/dubna/2018/courses/adria
nov.html
• (Гэри, Джонсон) Вычислительные машины
и труднорешаемые задачи
• (Пападимитриу, Стайглиц) Комбинаторная
оптимизация. Алгоритмы и сложность.
• CRLS

2. NP-полнота

Машина Тьюринга

3. Алфавит

Алфавитом называется конечное множество,
состоящее не менее чем из двух элементов и не
содержащее специального символа ⊔ .

4. Строки

• Обозначим через A множество всех
последовательностей (строк) длины n,
символами которых являются элементы
из алфавита A.
• Пусть A0 содержит ровно один элемент
пустую строку.
n
A : n A
n

5. Язык

• Языком над алфавитом A называется
произвольное подмножество из A*.
• Элементы языка часто называются словами.
n
• Если x A , то будем писать size(x) = n.

6. Машина Тьюринга (неформально)

• Машина Тьюринга состоит из N +1 оператора,
занумерованных от 0,…, N.
• Сначала выполняется оператор 0, и текущей позицией
строки является позиция 1.
• Каждый оператор работает по следующей схеме: считывает
элемент в текущей позиции, и в зависимости от его
значения переписывает элемент в текущей позиции на
некоторый элемент из A {⊔}, и, возможно, переходит на
одну позицию влево или вправо, и переходит на оператор,
который будет выполняться следующим.

7. Вход и оператор остановки

• На вход машине Тьюринга подается некоторая
строка x A* с символами из некоторого
фиксированного алфавита A.
• Можно считать, что слово записывается на
бесконечной с двух сторон ленте в ячейках с
номерами 1, 2, …, |x| по одному символу в ячейке.
Все другие ячейки содержат пустой символ ⊔.
• Существует специальный оператор –1, который
означает конец вычислений.

8. Машина Тьюринга (формально)

• Машина Тьюринга задается функцией
Φ:{0,…, N }× A {⊔}→{-1,…, N }×A {⊔}×{-1,0,1} для
некоторой N .
• Вычислением Φ x, x A* называется конечная
или бесконечная последовательность троек (n(i),s(i),π(i))
с n(i) {-1,…,N}, s(i) (A {⊔})Z и π(i) (i = 0,1,2,…),
которые определяются рекурсивно.
• n(i) означает текущий оператор.
• s(i) означает текущую строку.
• π(i) означает текущую позицию.

9. Машина Тьюринга (начало вычисления)

• n(0) := 0.
• sj(0) := xj для 1≤ j ≤ size(x), и
sj(0) := 0 для всех j ≤ 0 и j > size(x).
• π(0) := 1.

10. Машина Тьюринга (рекурсия)

• Пусть (n(i),s(i),π(i)) уже определено.
• Если n(i) ≠ -1, то пусть (m, , : (n(i , s (i( i .
• n(i+1) := m.
(i 1
s
• ( : ,
(i 1
(i
(i
s j : s j , j Z \ .
• π(i+1) := π(i) + δ.
i

11. Машина Тьюринга (конец вычисления)

Если n(i)= –1, то вычисление заканчивается
• time(Φ,x) = i
• output(Φ,x) {0,1}k,
где k =min{j ℕ:sj(i)= ⊔}-1
• (Φ,x)j= sj(i) для j =1,…k.
• Если последовательность бесконечна, то
• time(Φ,x) = ∞
• output(Φ,x) не определен.

12. Полиномиально вычислимая Машина Тьюринга

• Пусть A – алфавит, S, T A* два языка, и функция f :S T.
Пусть Φ – машина Тьюринга с алфавитом A.
Φ вычисляет f , если time(Φ,s) <∞ и (s ,output(Φ,s)) = f(s)
для каждого s S.
• Если существует полином p: time(Φ,s) ≤ p(size(s))
для всех s S , то Φ называется полиномиально
вычислимой машиной Тьюринга.
• T={0,1}
• Будем говорить, что Φ решает язык L:={s S : f(s) =1}.
• Если существует полиномиально вычислимая машина
Тьюринга, решающая язык L, то говорят, что L разрешим в
полиномиальное время.

13. Тезис Черча

• Любая интуитивно вычислимая функция
может быть вычислена на некоторой
машине Тьюринга.

14. Задачи распознавания (неформально)

• Любой язык L {0,1}* можно интерпретировать как задачу
распознавания: задана 0-1-строка, проверить принадлежит ли она L.
• Однако, нас более интересуют содержательные задачи (задача
Гамильтонов цикл: задан неориентированный граф, проверить есть ли
в нем Гамильтонов цикл.)
• Граф Лист смежности (матрица смежностей) бинарная строка
длины (O(n+m log n)).
• Для большинства интересных задач распознавания их примеры можно
представить как подмножества бинарных строк.
• Дополнительное требование: можно в полиномиальное время
проверить является ли произвольная строка примером
рассматриваемой задачи распознавания или нет.

15. Задачи распознавания (формально)

• Задачей распознавания называется пара
Π=(X,Y), где X – язык разрешимый в
полиномиальное время и Y X.
• Элементы X называются примерами из Π.
• Элементы Y называются «да»-примерами.
• Элементы X \ Y называются «нет»-примерами.
• Алгоритм для задачи распознавания (X,Y) – это
алгоритм вычисляющий функцию f : X {0,1},
такой что f(x)=1, если x Y, и f(x)=0, если x X \Y.

16. Класс P

• Класс всех задач распознавания, для которых существует
полиномиальный алгоритм, обозначается P.
• Другими словами, (X,Y) P, с Y X {0,1}*, когда оба
языка X и Y разрешимы в полиномиальное время.
• Доказательством того, что задача лежит в P, обычно
является полиномиальный алгоритм.
• Из тезиса Черча следует, что существует полиномиально
вычислимая машина Тьюринга для каждой проблемы в P.

17. Класс NP (неформально)

• К сожалению, принадлежность к классу P многих
интересных задач (Гамильтонов цикл, ЦЛП,
Вершинное покрытие, …) неизвестна.
• Вместо требования существования для задачи
полиномиального алгоритма потребуем, что для
каждого «да»-примера существует сертификат,
который может быть проверен в полиномиальное
время.
• Заметим, что мы не требуем сертификата для
«нет»-примера.

18. Класс NP (формально)

Задача распознавания Π=(X,Y) принадлежит NP, если
существует полином p и задача распознавания Π'=(X',Y')
из P, такие что
• X' = {x#c: x X, c {0,1}└ p(size(x))┘} и
• Y = {y X : c {0,1}└ p(size(x))┘ : y#c Y'}.
x#c обозначает соединение в общую строку строки x,
символа # и строки c.
Строка c: y#c Y' называется сертификатом для y.
Алгоритм для Π' называется алгоритмом проверки
сертификата.

19. P  NP

P NP
Утверждение 1.1 P NP.
• Выберем в качестве сертификата пустую строку
для всех «да»-примеров (то есть p = 0).
• Алгоритм для Π' удаляет последний символ входа
«x#» и затем применяет алгоритм для Π.

20. Пример задачи из NP

Утверждение 1.2
Задача Гамильтонов цикл принадлежит NP.
• Выберем в качестве сертификата любой
Гамильтонов цикл.
• Легко проверить за полиномиальное время,
является ли данный набор ребер Гамильтоновым
циклом.

21. Рандомизированный алгоритм

• Рандомизированный алгоритм для вычисления
функции f :S T задается алгоритмом, вычисляющим функцию g:{s#r: s S,r {0,1}k(s)} T.
• Для каждого примера s S алгоритм использует k(s)
случайных бит.
• Время работы алгоритма оценивается только от size(s).
• Рандомизированный алгоритм, работающий
полиномиальное время может использовать только
полиномиальное число случайных бит.

22. Лас-Вегас алгоритм

• Лас-Вегас алгоритмом называется
рандомизированный алгоритм такой,
что g(s#r) = f(s) для всех s S и всех
r {0,1}k(s).
• Лас-Вегас алгоритм всегда вычисляет
правильное решение, но время его работы
для одного и того же примера может
различаться.

23. Монте Карло алгоритм

• Монте Карло алгоритмом называется
рандомизированный алгоритм такой, что
существует ненулевая вероятность p
получения правильного ответа, то есть
r 0,1
k (s
p inf
s S
: g (s # r f (s
2
k (s
0.

24. Недетерминированный алгоритм

Если T = {0,1}, и для каждого s S с f(s) =
0 алгоритм вычисляет g(s#r) = 0 для всех
r {0,1}k(s), то такой алгоритм называется
рандомизированный алгоритм с
односторонней ошибкой.
Если, в дополнение, для каждого s S с
f(s) = 1 существует по крайней мере один r
{0,1}k(s) с g(s#r) = 1, то такой алгоритм
называется недетерминированным
алгоритмом.

25. Класс NP

Утверждение 1.3
Задача распознавания принадлежит NP тогда и
только тогда, когда для ее решения существует
полиномиальный недетерминированный алгоритм.

26. Доказательство

Задача распознавания Π=(X,Y) принадлежит NP, если
существует полином p и задача распознавания Π'=(X',Y')
из P, такие что
• X' = {x#c: x X, c {0,1}└ p(size(x))┘} и
• Y = {y X : c {0,1}└ p(size(x))┘: y#c Y'}
Полиномиальный алгоритм для Π' является полиномиальным недетерминированным алгоритмом для Π.
Пусть полиномиальный недетерминированный алгоритм
для Π использует k(x) бит для примера x. Тогда существует
полином p, такой что k(x) ≤ p(size(x)) для всех x.
Определим X' = {x#c: x X, c {0,1}└ p(size(x))┘} и
Y' = {x#c X' : g(x#r)=1, r состоит из k(x) первых бит с}.
Тогда (X', Y' ) P и
Y = {y X: c {0,1}└ p(size(x))┘ y#c Y' }.

27. NP-полнота

Теорема Кука

28. Полиномиальная сводимость

• Пусть Π1=(X1,Y1) и Π2=(X2,Y2) ― задачи
распознавания. Будем говорить, что Π1
полиномиально сводится (по Карпу) к Π2 ,
если существует функция f : X1 X2 ,
вычислимая в полиномиальное время такая,
что f(x) Y2 для всех x Y1, и f(x) X2\Y2
для всех x X1\Y1 .

29. NP-полнота

• Задача Π распознавания называется NP-полной,
если все другие задачи из класса NP
полиномиально сводятся к Π.

30. Набор значений истинности

• Пусть U={u1, u2,…, uk}―множество булевых переменных.
• Под набором значений истинности на множестве U
будем понимать функцию T: U {true, false}.
• Расширим T к множеству L : U u : u U ,
полагая T (u : true, если T (u : false, и наоборот.
• Элементы множества L называются литералами.

31. Дизъюнкция

• Дизъюнкцией над U называется множество литералов над
U.
• Она представляет дизъюнкцию этих литералов и
называется выполненной при некотором наборе значений
истинности тогда и только тогда, когда при
рассматриваемом наборе значений истинности хотя бы
один из ее членов принимает значение “true”.
• Семейство (набор) Z дизъюнкций над U называется
выполнимым в том и только том случае, если найдется
некоторый набор значений истинности на множестве U,
такой что выполнены все дизъюнкции из Z.

32. Задача «Выполнимость»

• Условие. Задано множество переменных U
и набор Z дизъюнкций.
• Вопрос. Является ли Z выполнимым?

33. Теорема Кука (1971)

Теорема 2.1
Задача «Выполнимость» является NP-полной.

34. Доказательство

• «Выполнимость» NP.

35. Доказательство сводимости

• Пусть Π=(X,Y) будет любая другая проблема в NP.
• Требуется доказать, что Π полиномиально сводится
к «Выполнимости».
• По определению существует полином p и задача
распознавания Π'=(X',Y') из P, такие что
• X' = {x#c: x X, c {0,1}└ p(size(x))┘} и
• Y = {y X : c {0,1}└ p(size(x))┘ : y#c Y'}.
• Пусть Φ:{0,…,N}× A {⊔}→{-1,…,N}×A {⊔}×{-1,0,1} –
полиномиальная машина Тьюринга для Π' с алфавитом A.
• Пусть полином q : time(Φ,x#c) ≤ q(size(x#c)) для всех
примеров x#c X'.
• size(x#c) = size(x) + 1 + └p(size(x))┘

36. Основная идея

• Сконструировать набор Z(x) дизъюнкций
над множеством V(x) булевых переменных
для каждого x X, так что Z(x) выполнимо
тогда и только тогда, когда x Y.

37. Булевы переменные

• Q:=q(size(x) + 1 + └p(size(x))┘)
• V(x):
– vijσ , 0 ≤ i ≤ Q, -Q ≤ j ≤ Q и σ A {⊔}= A
(после i шагов вычислений в j-й позиции строки
записан символ σ);
– wijn , 0 ≤ i ≤ Q, -Q ≤ j ≤ Q и −1≤ n ≤ N;
(после i шагов вычислений j-я позиция строки
просматривается и оператор n выполняется).

38. Итоговая цель

• Если (n(i),s(i),π(i)) i = 0,1,2,…тройка из
вычисления Φ, то требуется определить
набор дизъюнкций таким образом, что
– vijσ = true sj(i) =σ;
– wijn = true π(i) = j и n(i) = n;
– набор Z(x) дизъюнкций выполним
существует строка c, такая что
output(Φ,x#c)=1.

39. Требуемые условия для выполнимого набора дизъюнкций

• На каждом шаге вычислений каждая позиция содержит
единственный символ.
• На каждом шаге вычислений ровно одна позиция
просматривается, и один оператор выполняется.
• Вычисление начинается со входа x#c для
некоторого c {0,1}└ p(size(x))┘.
• Алгоритм работает корректно. ( (n,σ)=(m,τ,δ))
• Алгоритм останавливается, если n(i)=−1.
• Не просмотренные позиции не изменяются.
• Алгоритм на выходе получает 1.

40. На каждом шаге вычислений каждая позиция содержит единственный символ.

v : A 0 i Q, Q j Q;
v , v 0 i Q, Q j Q, , A : .
ij
ij
ij

41. На каждом шаге вычислений ровно одна позиция просматривается, и один оператор выполняется.

w : Q j Q, 1 n N 0 i Q;
ijn
w , w 0 i Q, Q j, j' Q, 1 n, n' N : ( j, n ( j' , n' .
ijn
ij 'n '

42. Вычисление начинается со входа x#c для некоторого c{0,1}└ p(size(x))┘.

Вычисление начинается со входа x#c для
некоторого c {0,1}└ p(size(x))┘.
v 1 j size (x ;
0, j , x j
v ( ;
v ( , v
w .
0,size x 1,#
0,size x 1 j , 0
0,1, 0
0,size( x 1 j ,1
1 j p(size (x ;

43. Алгоритм работает корректно. ((n,σ)=(m,τ,δ)).

Алгоритм работает корректно.
( (n,σ)=(m,τ,δ)).
v , w , v
ij
ijn
i 1, j ,
, v , w , w
ij
ijn
i 1, j ,m
0 i Q, Q j Q , A, 0 n N .

44. Алгоритм останавливается, если n(i) = −1.

w
i , j , 1
, wi 1, j , 1 , wi , j , 1 , vi , j , , vi 1, j ,
0 i Q, Q j Q, A.

45. Не просмотренные позиции не изменяются.

v , w , v
ij
ij 'n
i 1, j ,
0 i Q, A,
1 n N , Q j, j ' Q.

46. Алгоритм на выходе получает 1.

{vQ,1,1}, {vQ,2,⊔}

47. Полиномиальность сведения

• Длина записи Z(x)
O(Q3log Q)
– Число литералов
– запись индекса
O(Q3)
O(log Q)
• Так как Q ― это полином от size(x), то
существует полиномиальный алгоритм,
который по данному x, вычисляет Z(x).
• Осталось доказать, что Z(x) выполнима
тогда и только тогда, когда x Y.

48.

• Z(x) выполнима.
• набор значений истинности T, на котором выполнены
все дизъюнкции.
• Пусть c {0,1}└ p(size(x))┘,
и cj = 1 для всех j c T(v0,size(x)+1+j,1) = true,
и cj = 0 для всех j c T(v0,size(x)+1+j,1) = false.
• По построению переменные отражают вычисление на
входе x#c.
• output( , x#c)=1.
• ―алгоритм проверки сертификата.
• x ― «да»-пример (x Y).

49.

x Y и c ― любой сертификат для x.
Пусть (n(i),s(i),π(i)) i = 0, 1, …, m вычисление Φ x#c.
T(vi,j,σ ) = true sj(i) = σ
T(wi,j,n ) = true π(i) = j и n(i) = n.
T(vi,j,σ ) = T(vi-1,j,σ ) i = m + 1,…, Q.
T(wi,j,n ) = T(wi-1,j,n )
i = m + 1,…, Q.
T ― набор значений истинности, на котором выполнены
все дизъюнкции из Z(x).

50. Задача «3-Выполнимость»

• Условие. Задано множество переменных U
и набор Z дизъюнкций, каждая из которых
содержит ровно 3 литерала.
• Вопрос. Является ли Z выполнимым?

51. 3-Выполнимость

Теорема 2.2 (Cook 1971)
Задача «3-Выполнимость» является NP-полной.

52. NP-полнота

Основные NP-полные задачи

53. Задача «Независимое множество»

• Условие. Задан граф G=(V,E) и целое число k.
• Вопрос. Существует ли независимое множество
на k вершинах?
• Независимым множеством называется такое
подмножество вершин V′ V, что любые две
его вершины не соединены ребром в G.

54. Независимое множество

Теорема 3.1 (Karp 1972)
Задача «Независимое множество»
является NP-полной.

55. Идея доказательства

• «Выполнимость» → «Независимое множество»
• «Выполнимость»:
– множество переменных X,
– набор дизъюнкций Z ={Z1,…,Zm} c
Zi={λi1,…, λiki} (i = 1,…,m), где λij − литералы на X.
• Построим граф G, такой что G имеет независимое
множество размера m тогда и только тогда, когда
существует набор значений истинности, при
котором выполнены все m дизъюнкций.

56. Сведение

• Zi: клика на ki вершинах (вершина соответствует
литералу в дизъюнкции)
• Вершины разных клик связаны между собой
ребром, если они соответствуют литералу и его
отрицанию.
V (G : vij : 1 i m, 1 j ki
(
E (G : vij , vkl : (i k & j l & ij x & kl x : x X

57. Пример

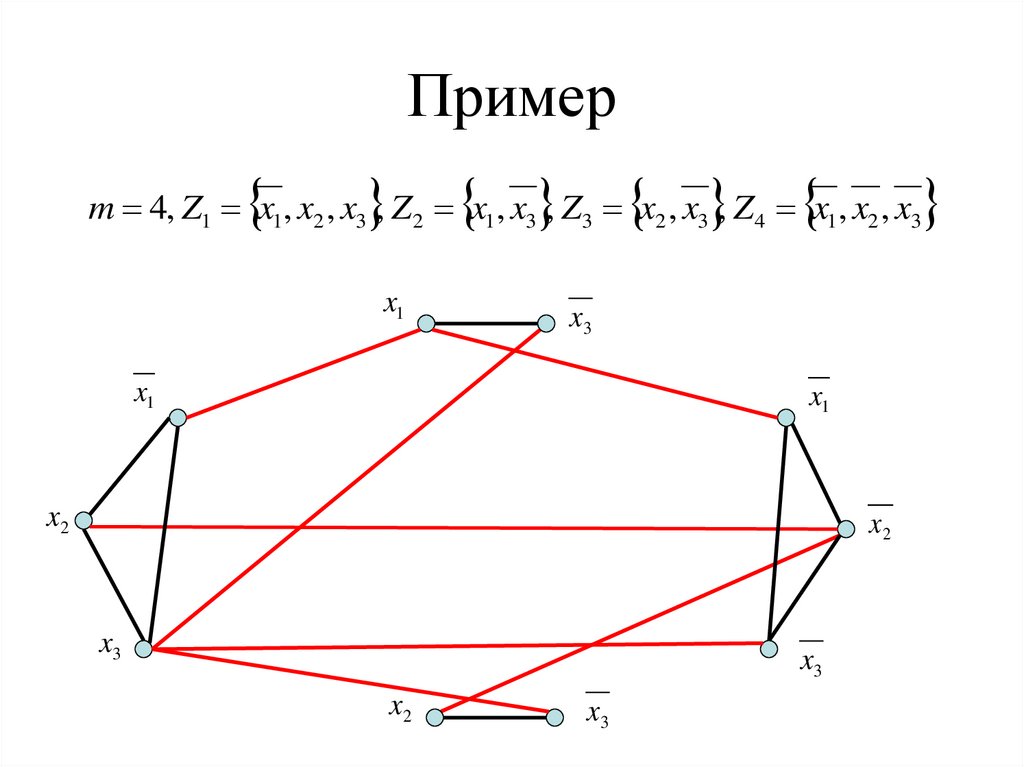
m 4, Z1 x1, x2 , x3 , Z2 x1, x3 , Z3 x2 , x3 , Z4 x1, x2 , x3
x1
x3
x1
x1
x2
x2
x3
x3
x2
x3

58. Доказательство

• Пусть в G есть независимое множество размера m.
• Тогда, оно содержит по одному элементу в каждой
клике и не содержит двух вершин,
соответствующих литералу и его отрицанию.
• То есть, эти вершины определяют по литералу в
каждой дизъюнкции.
• Положим каждому такому литералу значение true
и дополним до набора значений истинности,
который выполняет все дизъюнкции.

59. Доказательство

• Пусть существует набор значений
истинности, при котором выполнены
все m дизъюнкций.
• Выберем в каждой дизъюнкции один
литерал со значением true.
• Множество соответствующих вершин
определяет искомое независимое
множество.

60. Задача «Вершинное покрытие»

• Условие. Задан граф G и целое число k.
• Вопрос. Существует ли вершинное
покрытие мощности k?
• Вершинное покрытие это множество
вершин V′ V такое, что каждое ребро
имеет граничную точку в V′ .

61. Задача «Клика»

• Условие. Задан граф G и целое число k.
• Вопрос. Существует ли клика мощности k?
• Кликой называется такое подмножество
вершин V′ V, что любые две его вершины
соединены ребром в G.

62. Вершинное покрытие и клика

Теорема 3.2 (Karp 1972)
Задача «Вершинное покрытие» и задача «Клика»
являются NP-полными.

63. Задача «Гамильтонов цикл»

• Условие. Задан граф G.
• Вопрос. Существует ли в G
гамильтонов цикл?

64. Гамильтонов цикл

Теорема 3.3 (Karp 1972)
Задача «Гамильтонов цикл» является NP-полной.

65. Идея доказательства

• «Вершинное покрытие» → «Гамильтонов цикл»
• «Вершинное покрытие»: G = (V,E), k ≥ 0, целое.
• Построим граф G′ = (V′,E′), такой что G′ имеет
гамильтонов цикл тогда и только тогда, когда в G
есть вершинное покрытие H, состоящее из не
более чем k элементов.
• Пусть |E| = m.

66. Построение графа G′

• |V′| = 12m+k
• Каждому ребру (vi, vj) в исходном графе
соответствует 12 вершин uij1, uij2, uij3, uij4, uij5, uij6,
uji1, uji2, uji3, uji4, uji5, uji6.
• k дополнительных вершин a1, a2,…, ak.

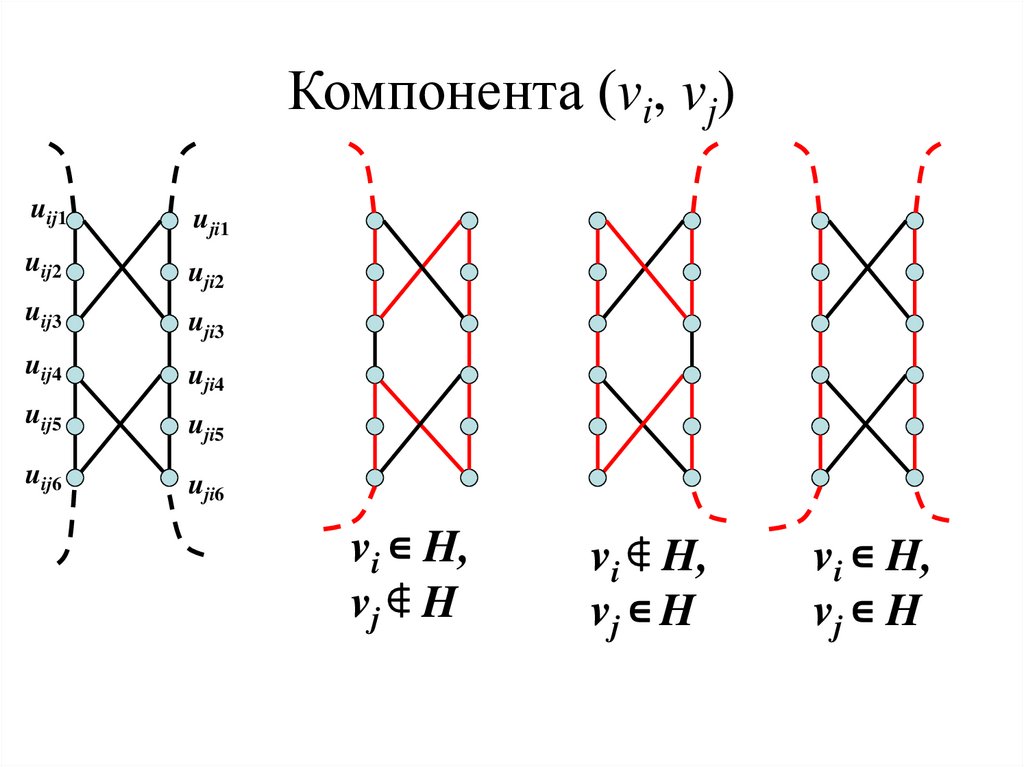
67. Компонента (vi, vj)

uij1
uji1
uij2
uji2
uij3
uji3
uij4
uji4
uij5
uji5
uij6
uji6
vi ∊ H,
vj ∉ H
vi ∉ H,
vj ∊ H
vi ∊ H,
vj ∊ H

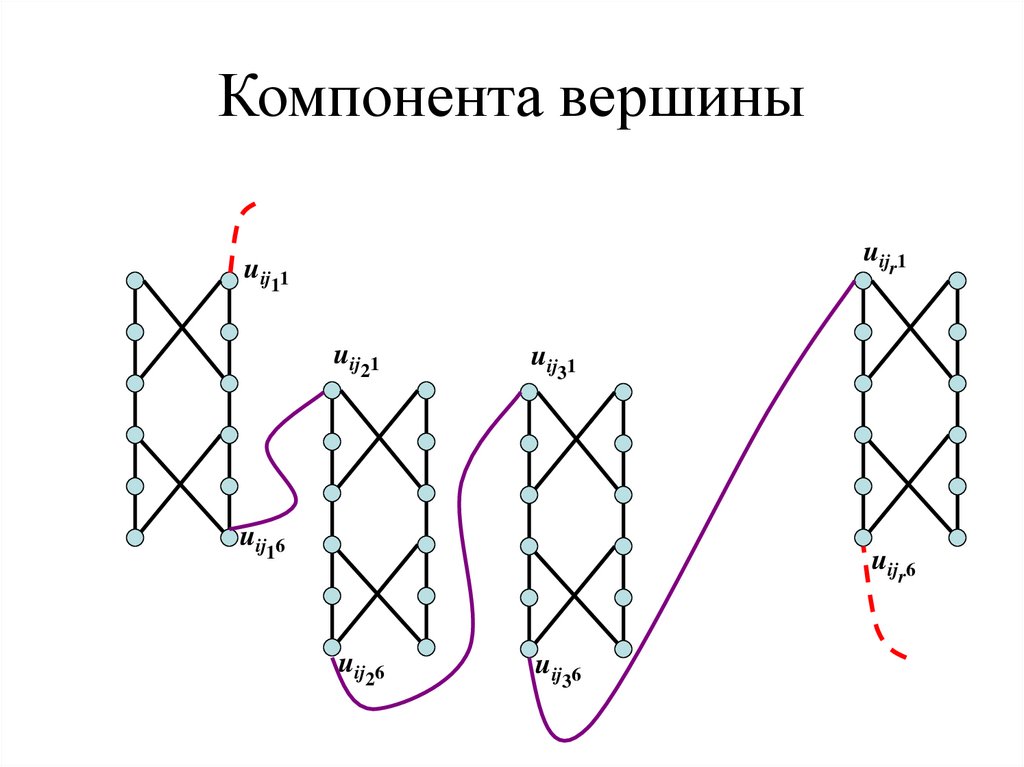
68. Компонента vi

• Пусть r степень вершины vi. Упорядочим
произвольным образом ребра, инцидентные vi: (vi,
vj1), (vi, vj2),…, (vi, vjr).
• Все компоненты, соответствующие ребрам,
инцидентным vi, соединяются вместе
следующими ребрами:
(u , u : 1 s r 1 .
ijs 6
ijs 11

69. Компонента вершины

uijr1
uij11
uij21
uij31
uij16
uijr6
uij26
uij36

70. Дополнительные вершины в G′

• Дополнительная вершина al соединена с первой и
последней вершиной компоненты vi. Пусть r
степень вершины vi.
(a , u : 1 l k , v V ,
(a , u : 1 l k , v V .
l
ij11
i
l
ijr 6
i

71. Компонента вершины

uijr1
uij11
uij21
uij31
uij16
uijr6
uij26
uij36