Программирование машин Тьюринга. Обоснование тезиса Тьюринга-Черча

1. Программирование машин Тьюринга. Обоснование тезиса Тьюринга-Черча.

2. Программирование машин Тьюринга

Работа машины задается функциональной схемой машины (таблица). Эта
функциональная схема представляет некоторый стандартный способ
задания алгоритма, который может называться тьюринговой программой.
Т.е. машина Тьюринга соответствует алгоритму, а не задаче.
Пример 1. Сложение.
Подается пара чисел. Результат-их
сумма. Работу машины нельзя
свести к стиранию *, т.к. возникает
пустая ячейка, а следовательно и
совокупность палочек нельзя
рассматривать как изображение
одного натурального числа.
| | | | | | * | | | |
| | | | | | | | | |
Согласно предлагаемой функциональной схеме работа машины будет
протекать так:

3.

| | | | | | * | | | |
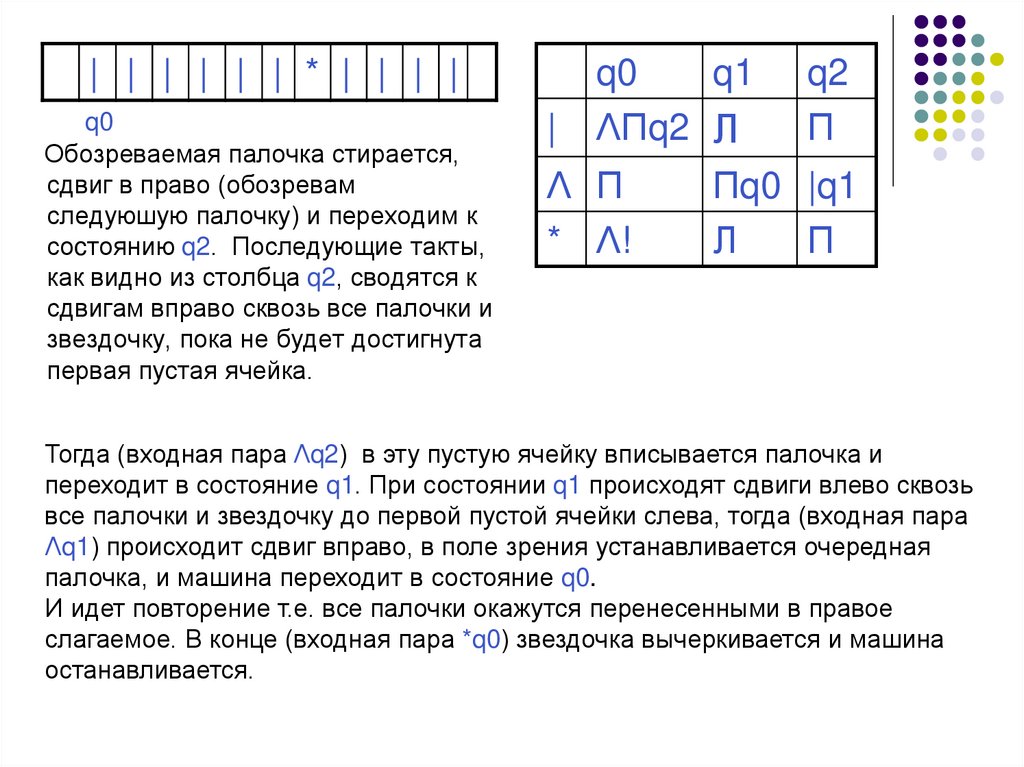
q0
Обозреваемая палочка стирается,
сдвиг в право (обозревам
следуюшую палочку) и переходим к
соcтоянию q2. Последующие такты,
как видно из столбца q2, сводятся к
сдвигам вправо сквозь все палочки и
звездочку, пока не будет достигнута
первая пустая ячейка.
|
q0
q1
ΛПq2 Л
Λ П
* Λ!
q2
П
Пq0 |q1
Л
П
Тогда (входная пара Λq2) в эту пустую ячейку вписывается палочка и
переходит в состояние q1. При состоянии q1 происходят сдвиги влево сквозь
все палочки и звездочку до первой пустой ячейки слева, тогда (входная пара
Λq1) происходит сдвиг вправо, в поле зрения устанавливается очередная
палочка, и машина переходит в состояние q0.
И идет повторение т.е. все палочки окажутся перенесенными в правое
слагаемое. В конце (входная пара *q0) звездочка вычеркивается и машина
останавливается.

4.

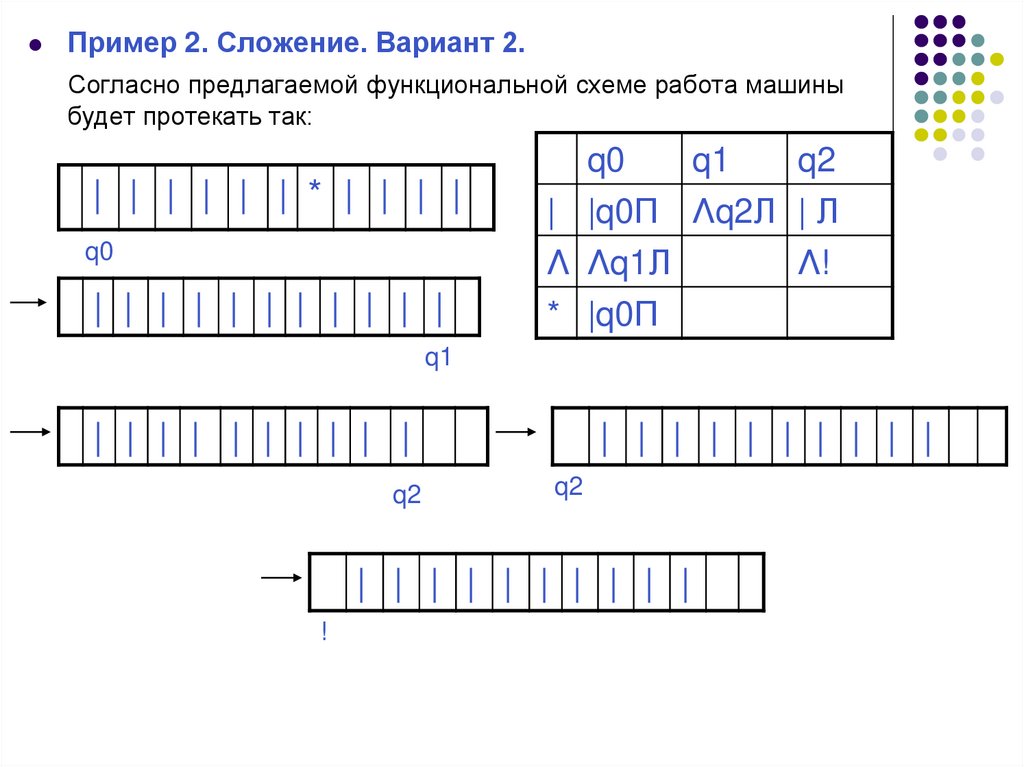
Пример 2. Сложение. Вариант 2.
Согласно предлагаемой функциональной схеме работа машины
будет протекать так:
q0
| | | | | | * | | | |
q0
| | | | | | | | | | |
q1
q2
| |q0П Λq2Л | Л
Λ Λq1Л
Λ!
* |q0П
q1
| | | | | | | | | |
q2
| | | | | | | | | |
q2
| | | | | | | | | |
!

5.

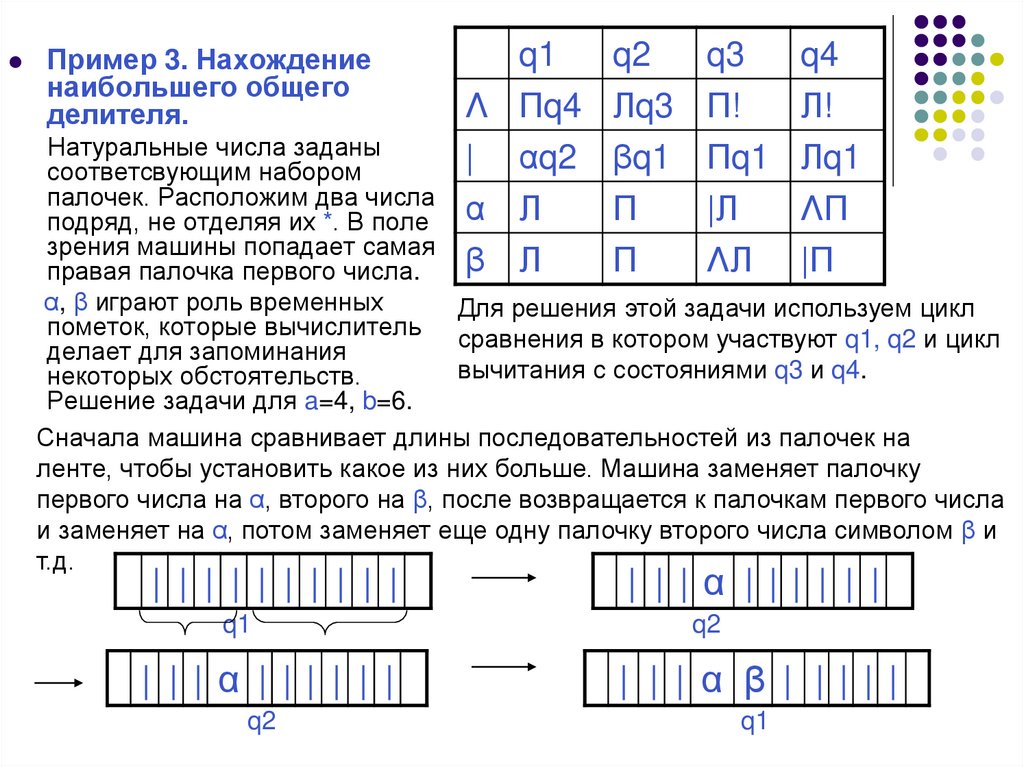
Пример 3. Нахождение
наибольшего общего
делителя.
q1
q2
q3
q4
Λ Пq4 Лq3 П!
Л!
| αq2 βq1 Пq1 Лq1
Натуральные числа заданы
соответсвующим набором
палочек. Расположим два числа
П
|Л
ΛП
подряд, не отделяя их *. В поле α Л
зрения машины попадает самая
β Л
П
ΛЛ |П
правая палочка первого числа.
α, β играют роль временных
Для решения этой задачи используем цикл
пометок, которые вычислитель сравнения в котором участвуют q1, q2 и цикл
делает для запоминания
вычитания с состояниями q3 и q4.
некоторых обстоятельств.
Решение задачи для a=4, b=6.
Сначала машина сравнивает длины последовательностей из палочек на
ленте, чтобы установить какое из них больше. Машина заменяет палочку
первого числа на α, второго на β, после возвращается к палочкам первого числа
и заменяет на α, потом заменяет еще одну палочку второго числа символом β и
т.д.
| | | | | | | | | |
q1
| ||α ||| | | |
q2
| ||α ||| | | |
| | | α β | ||||
q2
q1

6.

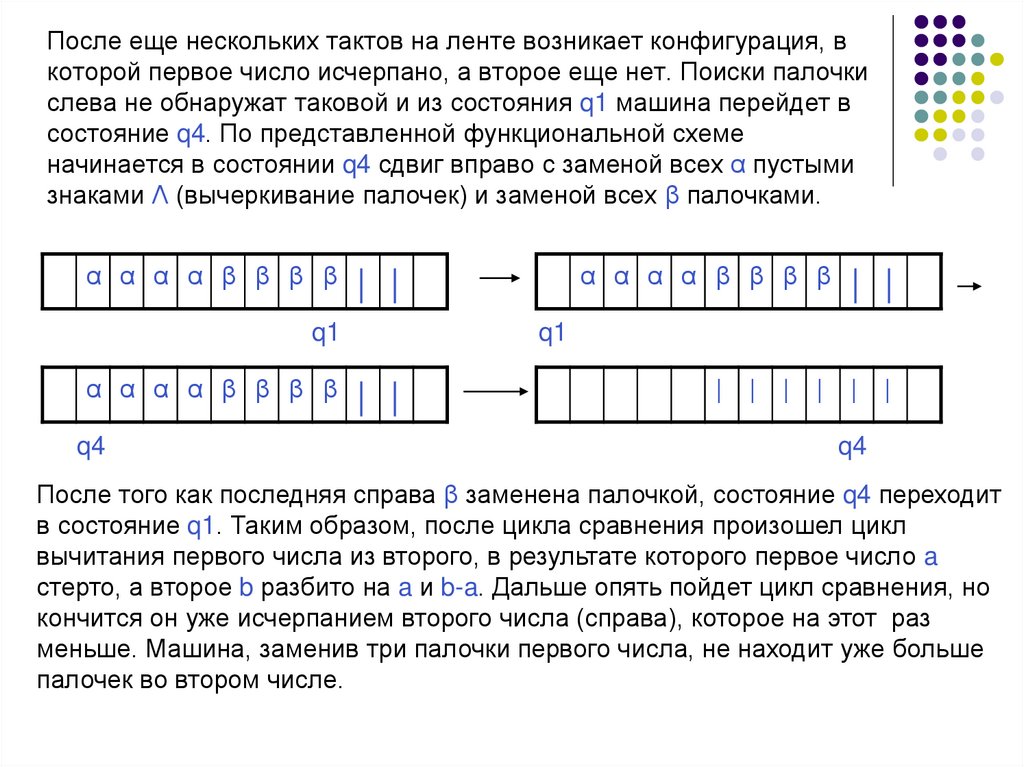
После еще нескольких тактов на ленте возникает конфигурация, в
которой первое число исчерпано, а второе еще нет. Поиски палочки
слева не обнаружат таковой и из состояния q1 машина перейдет в
состояние q4. По представленной функциональной схеме
начинается в состоянии q4 сдвиг вправо с заменой всех α пустыми
знаками Λ (вычеркивание палочек) и заменой всех β палочками.
α α α α β β β β
q1
α α α α β β β β
q4
α α α α β β β β
| |
| |
q1
| |
|
|
|
|
|
|
q4
После того как последняя справа β заменена палочкой, состояние q4 переходит
в состояние q1. Таким образом, после цикла сравнения произошел цикл
вычитания первого числа из второго, в результате которого первое число a
стерто, а второе b разбито на a и b-a. Дальше опять пойдет цикл сравнения, но
кончится он уже исчерпанием второго числа (справа), которое на этот раз
меньше. Машина, заменив три палочки первого числа, не находит уже больше
палочек во втором числе.

7.

|
|
|
|
|
|
|
α α α β β
q1
|
|
α α α β
|
|
q2
β
|
q3
q3
| | |
α α β
|
q1
β
q4
|
|
| |
q4
!
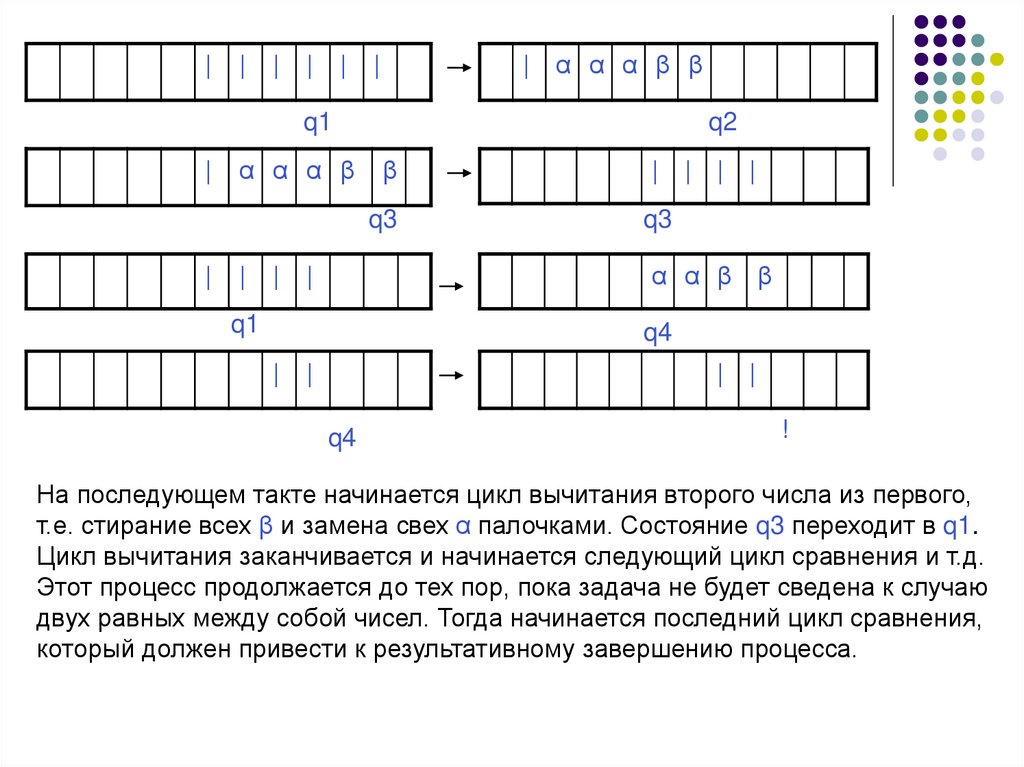
На последующем такте начинается цикл вычитания второго числа из первого,
т.е. стирание всех β и замена свех α палочками. Состояние q3 переходит в q1.
Цикл вычитания заканчивается и начинается следующий цикл сравнения и т.д.
Этот процесс продолжается до тех пор, пока задача не будет сведена к случаю
двух равных между собой чисел. Тогда начинается последний цикл сравнения,
который должен привести к результативному завершению процесса.

8.

Стандартные программы.
При построении новых программ (в частности, новых тьюринговых
программ) удобно использовать в качестве отдельных кусков
ранее построенные программы. Это возможно в случаях, когда
рассматриваемый алгоритм является сочетанием алгоритмов,
ранее уже изученных и построенных т.е. целесообразно
«запастись» тьюринговыми программами для тех алгоритмов, к
услугам которых приходится обращаться особенно часто.
Ниже приведены некоторые «служебные» алгоритмы:
Тождественный алгоритм (E) перерабатывает каждое слово Р в
некотором заданном алфавите в тоже самое слово Р. Е(Р)=Р.
Копирующие алгоритмы (Коп1-3.., Коп) Удваивающий алгоритм
Коп1 снимает одну копию заданного слова Р. / -разделительный
знак, не принадлежащий алфавиту, тогда Коп1(Р)=Р/Р. Для
утраивающего алгоритма Коп2 имеем: Коп2(Р)=Р/Р/Р. Для
Коп3(Р)=Р/Р/Р/Р и т.д. алгоритм, копирующий часть слова,
перерабатывает слово Р*R в слово P*R/R. Коп(Р*R)=P*R/R.
Заменяющий алгоритм (Зам ªα) Для заданной пары символов а и
α алгоритм Зам ªα заменяет всюду в слове Р вхождение буквы а на
α. Зам ªα (babaa) =(bαbαα).

9.

Выделяющий алгоритм (Выд) сохраняет из данного слова Р такую
его часть, которая указана специальными разделительными
символами. Алгоритм Выд перерабатывает слово Р в ту его часть,
которая расположена правее последнего вхождения разделительного
символа /. Выд (abb/aa/bab)=bab.
Алгоритм S вычисляет функцию s (x)= x+1; слово из x палочек
перерабатывает в слово из x+1 палочек.
Формальные операции над тьюринговыми программами.
Прежде чем приступать к описанию интересующих нас программ для
МТ, укажем две часто использующиеся формальные операции.
Переименование всех внутренних состояний за исключением
заключительного состояния «!». Если для программы U имело место
U(P)=R , то для преобразованной U’ так же справедливо U’(P)=R
Фиктивное расширение внешнего алфавита: к прежнему алфавиту
S={s1, s2,…, sk} добавляется новые символы s k+1, s k+2,…, s k+n,
соответственно к функциональной схеме добавляется новые n строк,
заполненных «!». Если для программы U имело место U(P)=R , то для
преобразованной U’ так же справедливо U’(P)=R.

10.

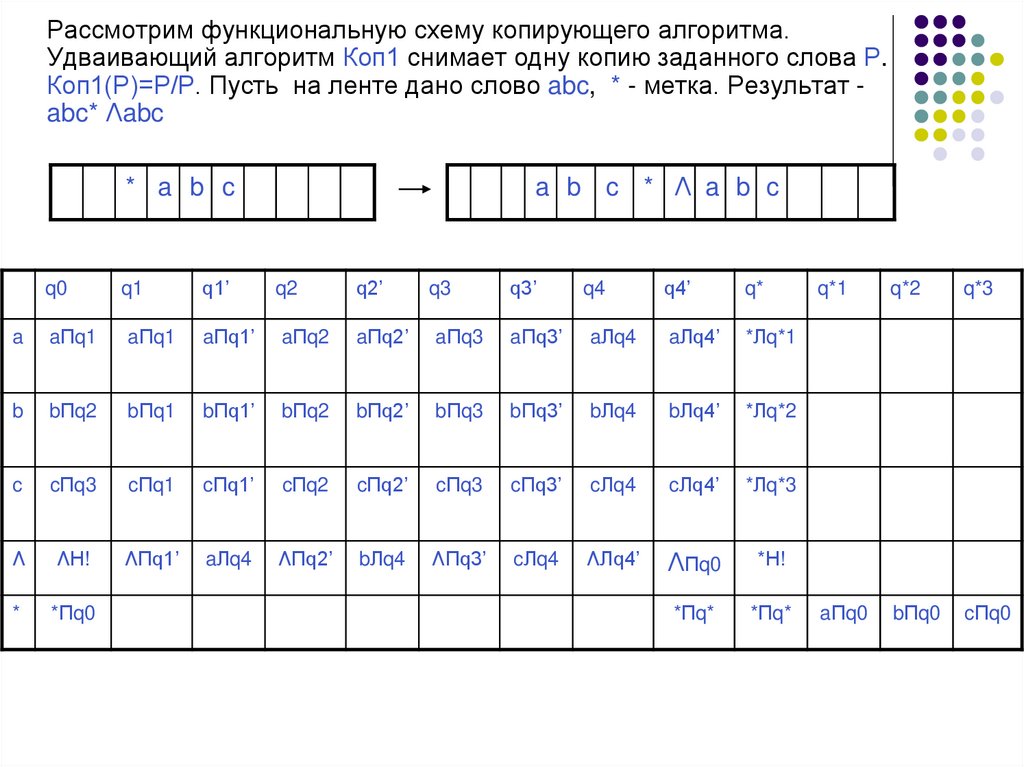
Рассмотрим функциональную схему копирующего алгоритма.
Удваивающий алгоритм Коп1 снимает одну копию заданного слова Р.
Коп1(Р)=Р/Р. Пусть на ленте дано слово abc, * - метка. Результат abc* Λabc
a b c * Λ a b c
* a b c
q0
q1
q1’
q2
q2’
q3
q3’
q4
q4’
q*
a
aПq1
aПq1
aПq1’
aПq2
aПq2’
aПq3
aПq3’
aЛq4
aЛq4’
*Лq*1
b
bПq2
bПq1
bПq1’
bПq2
bПq2’
bПq3
bПq3’
bЛq4
bЛq4’
*Лq*2
c
cПq3
cПq1
cПq1’
cПq2
cПq2’
cПq3
cПq3’
cЛq4
cЛq4’
*Лq*3
Λ
ΛН!
ΛПq1’
aЛq4
ΛПq2’
bЛq4
ΛПq3’
cЛq4
ΛЛq4’
ΛПq0
*Н!
*
*Пq0
*Пq*
*Пq*
q*1
q*2
q*3
aПq0
bПq0
cПq0

11.

Сначала обозревается метка в состоянии q0, машина оставляет ее и
переходит на первый символ слова a. Читает его и с помощью
запоминающего состояния q1 хранит, пока не будет команды q1’
поставить в ячейку символ а. Далее машина возвращается к началу
слова и переставляет местами символ а и метку *. Для того чтобы
больше не возвращаться к этому символу.
* a
b c Λ
Λ
а
* b
c
Λ а
Так машина будет пробегать по всему слову и в конце «снимет копии» всех
символов, поменяет местами метку * со всем словом abc и закончит свою
работу на пустом символе Λ.
a * b
c Λ a
a b *
c Λ a b c
a b *
a b c
*
c
Λ a b
Λ a b c

12. Обоснование тезиса Тьюринга-Черча.

Тезис Тьюринга-Черча.
тезис Тьюринга-Черча гласит: Любая функция, которая может быть
вычислена, может быть вычислена машиной Тьюринга.
тезис Тьюринга-Черча утверждает, что машина Тьюринга на самом
деле определяет то, что в математике понимают под алгоритмической
(или выполнимой, или рекурсивной, или механической) процедурой.
Один из аргументов в пользу тезиса – реализуемость четырех
основных типов сочетаний алгоритмов. С помощью этих четырех типов
сочетаний и уже построенных алгоритмов можно записывать все более
и более сложные алгоритмы.

13.

Четыре важных типов сочетания алгоритмов.
Последовательная композиция. Рассматривается сочетание
двух программ U, V. Сначала применяется алгоритм U, а затем к
его результату, т.е к слову U(P), применяется алгоритм V и,
следовательно, получается слово V(U(P)).
Каковы бы ни были тьюринговы программы U и V, может быть
эффективно построена тьюрингова программа T такая, что для
всех рассматриваемых слов Р: T(P)= V(U(P)).
Обе программы объединяем в одну программу T и в подпрограмме
U всюду заменяем символ «!» на начальное состояние программы
V. Когда программа V включается в работу, ею обозревается та
ячейка, в которой закончила работу программа U.
q1 ……qu
r1 ……rt
s0
.
.
sm
U
r1 вместо !
V

14.

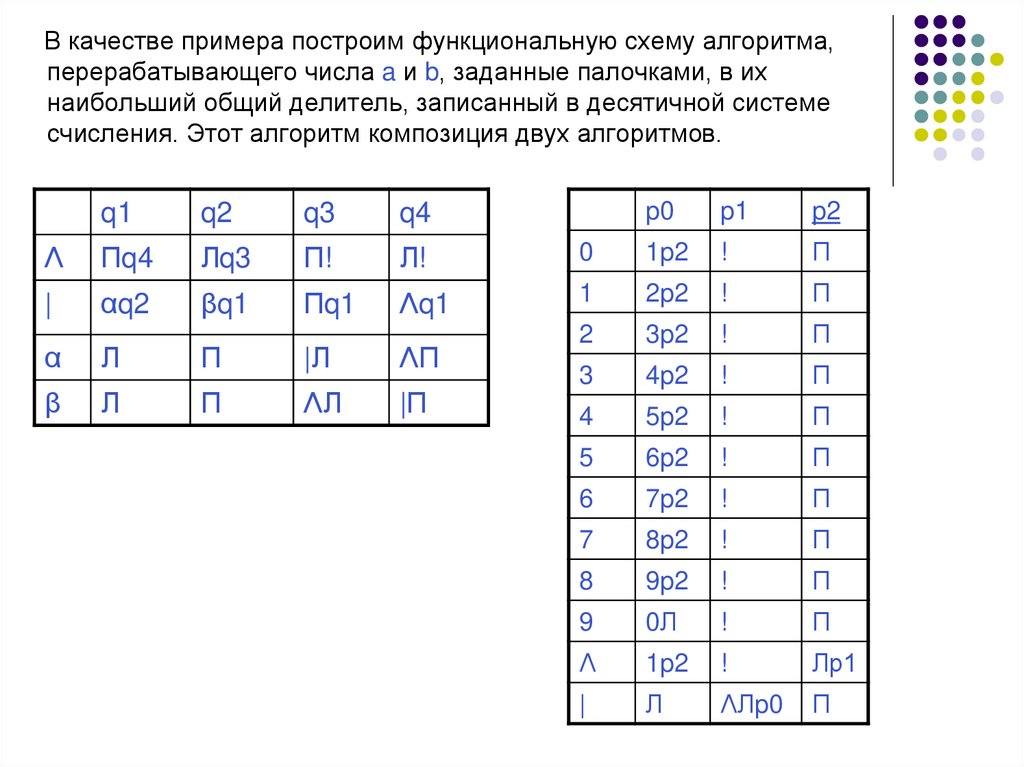
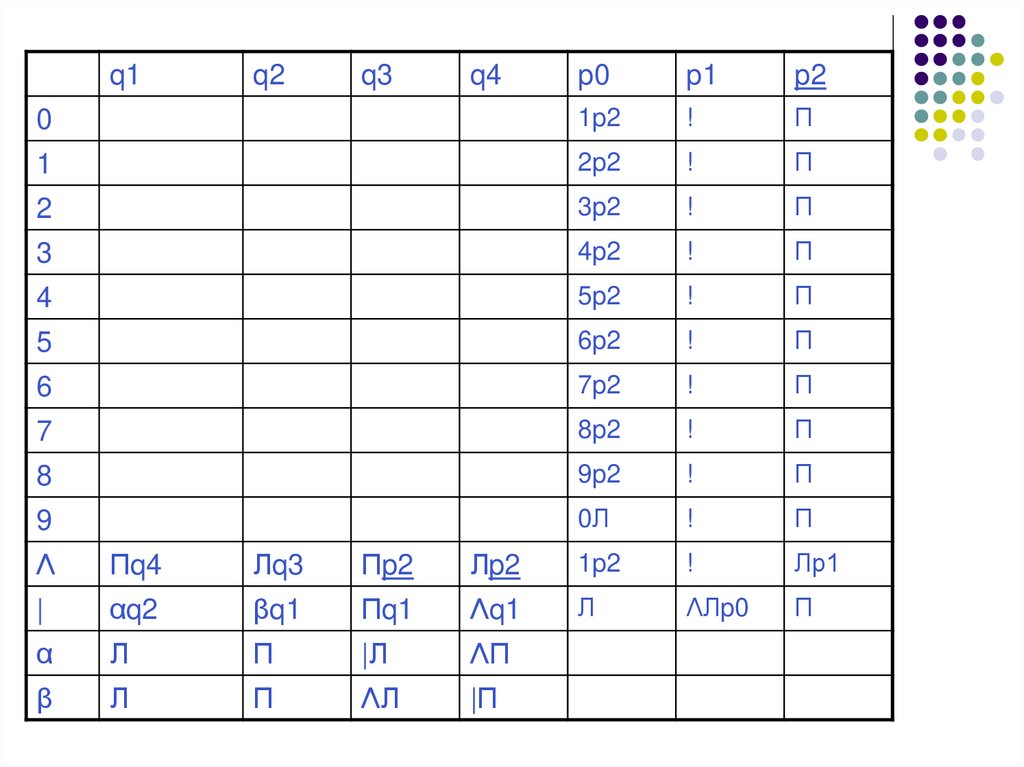
В качестве примера построим функциональную схему алгоритма,
перерабатывающего числа a и b, заданные палочками, в их
наибольший общий делитель, записанный в десятичной системе
счисления. Этот алгоритм композиция двух алгоритмов.
q1
q2
q3
q4
Λ
Пq4
Лq3
П!
Л!
|
αq2
βq1
Пq1
Λq1
α
Л
П
|Л
ΛП
β
Л
П
ΛЛ
|П
p0
p1
p2
0
1p2
!
П
1
2p2
!
П
2
3p2
!
П
3
4p2
!
П
4
5p2
!
П
5
6p2
!
П
6
7p2
!
П
7
8p2
!
П
8
9p2
!
П
9
0Л
!
П
Λ
1p2
!
Лр1
|
Л
ΛЛp0
П

15.

q1
q2
q3
q4
p0
p1
p2
0
1p2
!
П
1
2p2
!
П
2
3p2
!
П
3
4p2
!
П
4
5p2
!
П
5
6p2
!
П
6
7p2
!
П
7
8p2
!
П
8
9p2
!
П
9
0Л
!
П
Λ
Пq4
Лq3
Пp2
Лp2
1p2
!
Лр1
|
αq2
βq1
Пq1
Λq1
Л
ΛЛp0
П
α
Л
П
|Л
ΛП
β
Л
П
ΛЛ
|П

16.

Параллельная композиция. Рассматривается совместная работа
алгоритмов U и V применительно к исходным данным. Данные слова Р и Н и / - некоторый символ, не встречающийся в алфавитах.
Тогда Р/Н и U(P)/V(Н) - изображения пар исходных слов и пар
результирующих слов – это и называется параллельной композицией
алгоритмов U и V.
Пример: входное слово 389/ ||||||*|||| . Композиция увеличит на
единицу десятичное число 389 и найдет сумму слагаемых 6+4 и
выдаст результат 390/||||||||||.
Для любых тьюринговых программ U и V может быть эффективно
построена тьюрингова программа T, такая что для всех слов Р, Н в
соответствующих алфавитах T(P/H)=U(P)/V(H).
Доказательство этого утверждения так же, как и в случае
последовательной композиции, заключается в описании подходящего
способа, который строит программу T. Программа должна быть
устроена так чтобы она сначала перерабатывала кусок Р слова Р/Н,
затем перерабатывала кусок Н и, наконец, свела бы полученные
результаты по обе стороны от символа /. Трудность, которая
возникает в этом случае состоит в том, что, воспроизводя работу
программы U применительно к куску Р, машине может мешать кусок
Н. Точно так же работе V на куске Н может мешать кусок Р или те
записи, которые возникли бы в результате его обработки.

17.

Конечно, положение упростилось бы, если вместо одной ленты
машины Тьюринга в качестве внешней памяти имелись бы две ленты.
В таком случае можно было бы вычисление U(P) осуществить на
одной ленте, вычисление V(H) на другой, и потом свести результат
вместе.
Для лучшего понимания «успешной эксплуатации» внешней памяти,
надо рассмотреть машины с особенностями внешней памяти, т.е
ленты. Сначала рассмотрим машину с правой полулентой, т.е
бесконечной только в одну сторону – а именно вправо. Ячейки ленты
занумерованы числами 0,1,2,.. В нулевой ячейке помещен
специальный знак /.
0
/
1
2
P(1) P(2)
k
………………..
P(k)
Команды машины и их выполнение имеют такой же вид, как обычно, с
единственной оговоркой: в каком бы состоянии машина ни обозревала знак /,
команда предусматривает сдвиг вправо без изменения самого символа /. Иначе
говоря, если в процессе вычисления головка достигнет нулевой ячейки
(обозревается символ /),то после она покидает ее и возвращается вправо.
Аналогично определяется машина с левой полулентой.
k
3
2
1
0
P(1)
P(2)
………………..
P(k-2) P(k-1)
P(k) /

18.

В начальной конфигурации слово P расположено на краю полуленты
и обозревается первый (слева) символ. Результат – слово R –
записано левее символа / и в нем так же обозревается первый
слева символ.
Очевидно, что функциональную схему любой машины с полулентой
можно перестроить в функциональную схему обычной машины
Тьюринга. Отсюда следует, что все проблемы, которые можно
решать на машинах с полулентой, можно решать и на обычных
машинах.
Пусть задана машина с полулентой, обозначим ее W. Тогда
программа для машины Тьюринга имеет вид T=N°W°M т.е является
последовательной композицией трех схем. N переводит слово P в
слово /P и возвращает головку к первой букве слова P, программа M
отыскивает символ / левее результата R, стирает его и возвращает
головку к первому символу этого слова.
Справедливы следующие утверждения:
Существует алгоритм, который любую тьюрингову программу T
перерабатывает в программу (/T) для машины с правой
полулентой; при этом выполняются условия: а) T(P)=R тогда и
только тогда, когда (/T)(P)=R; б) в машине /T результат R (так
же как и P) записан на краю полуленты.
По T строится программа (T/) для машины с левой полулентой.

19.

Прежде чем привести соответствующие доказательства, покажем как
из этих утверждений выводится теорема о программировании
параллельной композиции U(P)/V(H) двух алгоритмов U(P) и V(H).
Сначала строим программы U/ и /V, затем формируем U/V как
композицию четырех программ:
1) (U/) перерабатывает слово P/H в U(P)/H.
2) стандартная программа M1 перемещает головку с первой буквы
слова U(P) к первой букве слова H.
3) (/V) продолжает переработку до выдачи слова U(P)/V(H), причем
обозревается первая буква из V(H).
4) стандартная программа M2 перемещает головку с первой буквы
V(H) к первой букве U(P).
Теперь перейдем к доказательству приведенных выше утверждений.
Доказательство: Для определенности рассмотрим случай с правой
полулентой. Пусть задана программа T(P)=R, где P - исходное слово,
R - результат выполнения программы T. Программа /T строится как
последовательная композиция трех программ N°T’°M из которых
основную нагрузку несет программа T’ (расширенная программа T).
Программы N, M – стандартные и выполняют вспомогательные
функции. Так же будем считать, во избежание громозскости, что
помимо пустого символа Λ в исходной программе T имеются лишь два
«значащих» символа x и y.

20.

1. Рассмотрим работу программы N. Сначала программа N вписывает
символ # в первую пустую ячейку исходного слова P.
0
1
2
k
/
P(1)
P(2)
………………..
P(k)
r1
Тем самым слово ограничивается на ленте символами / и # .
/
P(1)
P(2)
………………..
P(k) #
!
2. Далее в процессе работы программы T’ символ /
(неподвижная метка) сохраняется в своей ячейки, а символ #
(подвижная метка) перемещается вправо каждый раз когда
выясняется, что внутри зоны (между / и #) не хватает места
для вычислений. К концу работы программы T’ в зоне,
которая сложится к тому времени, будет расположена запись
слова R – резутьтата. Программа T’ получается путем
расширения программы T. Алфавит {x, y, Λ} расширяется за
счет символов / и #. Далее для каждого состояния q
программы T добавляются еще 7 связанных с q состояний: q’,
q/, qx, qy, qΛ, q#, q”. Ниже представена функциональная
схема программы T’.

21.

… q
… q’
x
y
T
Λ
#Лq
#
ΛПq’
/
Пq/
q#
q”
q/
qx
qy
qΛ
ΛПqx
xПqx
yПqx
ΛПqx
Л
ΛПqy
xПqy
yПqy
ΛПqy
Л
ΛПqΛ
xПqΛ
yПqΛ
ΛПqΛ #Лq”
Л
xПq#
yПq#
ΛПq#
(***)
Пq
Сравним работу программы T и Т’. Пока головка находится внутри зоны, T’
работает как T. Допустим, что в некоторое время головка вышла на # в
некотором состоянии q. Тогда она стирает # (команда #q ΛПq’) уходит
вправо в пустую ячейку, вписывает в нее # (команда Λq’ #Лq) и
возвращается в состоянии q туда, где прежде была метка #.
/
x
x
y
y
x
#
q
/
x
x
y
y
x
#
q

22.

Пусть, головка машины вышла за метку / в состоянии q.
/
x
x y y
x #
q
Поскольку метка / неподвижна, то зону нельзя расширить влево.
Следовательно, необходимо высвободить, для дальнейшей работы программы
Т, на левом конце ленты пустую ячейку. Для этого всю запись в зоне, включая и
метку #, перемещают на одну ячейку вправо, а в освободившуюся пустую
ячейку по соседству с меткой / помещают головку в том состоянии q, в котором
она первоначально(в поиске свободного места) наткнулась на знак /. Тем
самым и достигается нужный эффект от программы T’.
/
x
x y y
x #
q
Рассмотрим подробнее: наткнувшись на / в состоянии q, головка уходит вправо,
(команда /q Пq/), очищает соседнюю справа ячейку, запоминая ее содержимое,
и уходит снова вправо(команда xq/ ΛПqx, где qx запоминает х). Из столбцов
таблицы (***) видно, что процесс перенесения содержимого каждой ячейки в
соседнюю с ней ячейку справа продолжится до тех пор, пока головка не
переместит символ #. После, головка начнет сдвиг влево в состоянии q’, пока
не дойдет до пустой ячейки, соседствующей со знаком /.

23.

3. Заметим, что после окончании работы T’ результат R записан в
удлинившейся по ходу работы зоне. Программа M результат R
перемещает впритык к метке / и в конце программа удалит
подвижную метку #.
Функциональная схема программы М.
py’
px
x
Λ Лpx
Пpx’ Пpy’
Л
y
Λ Лpy
Пpx’ Пpy’
Л
Λ
П
Л
#
ΛЛp2
/
py
px’
p1
Л
p2
хПp1 уПp1 Л
Л
Пpx’ Пpy’
П!

24.

Разветвление алгоритмов (Условный оператор If… then).
Рассматривается применение к исходным данным алгоритма U или V в
зависимости от того, обладают ли эти данные некоторым свойством.
Для решения этой задачи мы располагаем распознающим алгоритмом
F, который применим к данным и дает ответ «да» (обладают свойством)
или «нет» (если данные не обладают свойством). Если F тьюрингова
программа применимая к слову Р, то F выдает 1, если ответ
утвердительный, и 0- если ответ отрицательный. т.е «если F, то U
иначе V».
Каковы бы ни были тьюринговы программы U и V и распознающая
программа F, применимые к словам в одном и том же алфавите A,
может быть построена тьюрингова программа T, такая что для
всех слов P из A:
T(P)= U(P), если F(P)=1
V(P), если F(P)=0
Опишем программный алгоритм, который строит программу T, исходя из
программ U, V, F. Будем использовать последовательную и
параллельную композиции, тождественный алгоритм Е, удваивающий
алгоритм Коп1, программу ветвления Ветв ( состояния p, p0, p1,
внешние символы 0, 1, /, команды 1p ΛПp1; /p1 ΛПq1;
0р ΛПр0; /р0 ΛПr1)

25.

Построим сначала программу F’, которая в применении к слову Р
работает так: перерабатывает Р в 1/Р или в 0/Р в зависимости от
F(P)=1 или F(P)=0. В качестве F’ можно взять Коп1; (F/E).
Программа Т имеет вид композиции ( F’; Ветв (U, V)):
t1…tn
Р(1) Р(2) .......
F’
Р(J)
/
P(1)
…..
P(J)
2
/
P(1)
……
P(J)
3
P(J)
4
P(J)
5
!
σ
Ветв
U
V
p вместо «!»
t1
σ
p p0 p1 q1…qm r1…ri
p
P(1) P(2)
……
q1 программа U
P(1) P(2)
……
r1 программа V
Заключительное состояние «!» в F’
заменяется состоянием р из Ветв, а
состояния q1, r1 заменяются на
начала программ U, V. В качестве
начала T берем начальное состояние
t1 программы F’...В соответствии с
изображением слова Р, сначала
работает подпрограмма F’, и вместо
заключительной конфигурации 2,
появляется 3, здесь σ =0 или 1. После
включается Ветв и получим 4, если
σ=1, или получим 5, если σ=0. Т.о.
обеспечивается работа или U или V.

26.

Повторное применение алгоритма (Цикл while…do). Будем
пользоваться предыдущим примером. Заменим V на стандартную Е,
а в программе U состояние «!» заменим начальным состоянием t1
подпрограммы F’; t1 будет начальным состоянием для всей
полученной программы T’. Программа T’ применительно к слову P
будет работать так: 1) проверяем условие F применительно к Р.
(F(P)=1 или F(P)=0). 2) Если «да», то Р перерабатывается по
программе U в слово U(P), но на этом работа не прекращается. 3)
проверяется условие F применительно к слову U(P). Если «да», то
выполняется U(U(P)). 4) после условие F будет проверяться
применительно к этому слову и т.д. Это будет выполняться до тех
пор, пока впервые не получится слово, не обладающее свойством F.
Тогда процесс останавливается и это слово (им можем оказаться и
само слово Р), объявляется результатом. В противном случае
процесс никогда не останавливается и получается
последовательность слов U(P), U(U(P)), U(U(U(P))),... т.е. идет
повторение алгоритма U, пока выполняется условие F. «Пока
F,повторяй U».
Каковы бы ни были тьюрингова программа U и распознающая
тьюрингова программа F, можно эффективно построить тьюрингову
программу T’ для алгоритма «пока F,повторяй U».

27.

Языки программирования.
Посредством рассмотренных выше сочетаний алгоритмов можно
записать естественным образом более сложные выражения,
описывающие более сложные алгоритмы. Т.о. можно ввести язык
формул или входной язык программирования (язык высокого уровня).
Рассмотрим алгоритм Евклида, описание которого записывается в виде
следующей формулы входного языка.
(пока V2, повторяй (если V1, то U1, иначе U2))°U3
(*)
где ° последовательная композиция. Данная формула описывает
алгоритм Евклида с большим количеством циклов.
Здесь формула (если V2, то (если V1,то U1, иначе U2), иначе U3) в
точности описывает один цикл алгоритма Евклида.
Следовательно, если уже имеются тьюринговы программы
V1,V2,U1,U2,U3, то посредством «трансляции» операторов композиции,
ветвления, повторения можно получить из вышеописанной формулы (*),
тьюрингову программу для алгоритма Евклида.

28.

Используемые ресурсы:
Б. А. Трахтенброд «Алгоритмы и вычислительные автоматы» -М.
изд. «Советское радио» 1974.
Х. Роджерс «Теория рекурсивных функций и эффективная
вычислимость» - М. изд. «Мир» 1972.
С. М. Крылов «Модели универсальных дискретно-аналоговых
вычислительных машин на основе машины Тьюринга» изд.
"Электронное моделирование", 1982, № 3.

29.

Вопросы самоконтроля:
Чему соответствуют машины Тьюринга и каким образом они
представляются?
Перечислите стандартные программы и напишите программу
для одной из них.
Что утверждает тезис Тьюринга-Черча и каким образом его
можно обосновать?
Последовательная композиция. Ее функционирование?
Параллельная композиция. Преобразование машины с
полулентой в функциональную схему обычной машины
Тьюринга.
Разветвление алгоритмов. Повторное применение алгоритма.
Условие зацикливания процесса?
Что такое язык формул?

30.

ВСЕМ СПАСИБО ЗА ВНИМАНИЕ !

31.

Приложение
Моделирование на МТ рекурсивных
функций

32.

Рекурсивные функции и функции,
вычислимые по Тьюрингу.
Выше были рассмотрены тьюринговые программы
для вычисления суммы и нахождения наибольшего
общего делителя. Конечно, это не единственные
задачи, решаемые машиной Тьюринга, можно
построить программы для многих других часто
встречающихся числовых функций например
(x², x³, …, x!, 2ⁿ, …, и т.д.).
Применяя входной язык программирования, можно
обнаружить, что класс вычислимых по Тьюрингу
функций необычайно широк, и он охватывает все
функции, которые описываются посредством так
называемых индуктивных определений.
Далее будет показано, что класс вычислимых по
Тьюрингу функций охватывает все т.н. рекурсивные
функции.

33.

Введем обозначения Uf –программа МТ, вычисляющая функцию
f. Ближайшая цель- описать операторы трех типов –
простейшие, примитивной рекурсии, μ-оператор – и показать,
что класс вычислимых по Тьюрингу функций замкнут
относительно этих операторов.
Простейшие операторы.
К ним относятся операторы суперпозиции и введения фиктивных
аргументов. Путем введения фиктивных аргументов заданная
функция f может быть преобразована в функцию h от большего
числа аргументов; Например, по заданной одноместной функции
f(x) можно определить двухместную функцию h следующим
условием h(x,y)=f(x). Можно ввести одновременно несколько
фиктивных переменных, например h(x,y,u,v)=f(y,v). Во всех таких
случаях построение Uh по Uf совершенно очевидно.
Из заданных функций путем подстановки функций вместо
аргументов можно образовать новые функции (сложные,
функции от функций); в этом и заключается действие оператора
суперпозиции.

34.

Рассмотрим одноместную функцию φ(x), определяемую суперпозицией
одноместных функций f и g: φ(x)=g(f(x)). Формула Uf°Ug описывает
алгоритм вычисления функции φ и по ней с помощью оператора
последовательная композиция может быть получена тьюрингова
программа Uφ. Аналогично строится программа в случае суперпозиции
многоместных функций. Пусть φ(x1,x2) определена как суперпозиция
g(f1(x1,x2), f2(x1,x2), f3(x1,x2)). Тогда Uf строиться в соответствии с
формулой:
Коп2°(Uf1||Uf2||Uf3)°Зам||* °Ug
Исходя из слова х1*х2 , алгоритм Коп2 делает две его копии и
вырабатывает слово х1*х2||x1*x2||x1*x2, которое перерабатывается
параллельной композицией Uf1||Uf2||Uf3 в слово
f1(x1,x2)||f2(x1,x2)||f3(x1,x2). После этого применяется алгоритм Ug, но
предварительно заменяем символ || на *, что делает алгоритм Зам||*.
Необязательно, чтобы f1, f2,.. зависели от одних и тех же аргументов
или даже, чтобы число аргументов было у них одним и тем же. Пусть
φ(x,y,u,z)=g(f1(x,y),f2(x),f3(x,u,z)), программу Uφ можно построить исходя
из Uf1,Uf2, Uf3, Ug, но удобнее составить Uh1, Uh2, Uh3. т.е
h(x,y,u,z)=f1(x,y),h2(x,y,u,z)=f2(x),h3(x,y,u,z)=f3(x,u,z). Далее строим
программу Uφ исходя из «стандартной» суперпозиции
φ(x,y,u,z)=g(h1(x,y,u,z), h2(x,y,u,z), h3(x,y,u,z))

35.

Примитивная рекурсия.
Сначала рассмотрим простую разновидность примитивной
рекурсии – итерацию.
Пусть задана одноместная функция f и фиксированное число c.
Тогда числа c, f(c), f(f(c)), f(f(f(c))),.. можно рассматривать как
значаения φ(0), φ(1), φ(2), φ(3),.. некоторой новой функции φ. Ее
определение может сформулировано так: φ(0)=с –
базис(начальное значение функции), φ(х+1)=f(φ,(x)) –
индукционный шаг (рекуррентное соотношение, позволяет от
искомого значения φ(х+1) вернуться к ранее вычисленному
φ(х)). Пример: f(x)=2**x, c=1 получаем φ(0)=1, φ(x+1)=2φ(x).
Данные соотношения определяют показательную функцию
φ(n)=2ⁿ. Такой способ определения функции φ называют
итерацией функции f при начальном значении с.
Пример: с=1, f(x,y)=(x+1)*y получаем примитивную рекурсию
φ(0)=1, φ(х+1)=(х+1)*φ(х). Видно, что φ(1)=1*1=1, φ(2)=2*1=2 и
т.д Общее φ(х)=х*(х-1)*(х-2)...2*1=х!
Может оказаться, что один из аргументов функции f фиктивен,
например f(x,y)=q(y), тогда рекурсивная схема имеет вид φ(0)=с,
φ(х+1)=q(φ(x)) и она определяет φ как итерацию функции q.

36.

μ – оператор.
Пусть f(x,y)– предикат, т.е функция принимающая два значения 0 и 1.
Зададим функцию φ(х), при фиксированном хº, для которого существует
хотя бы одно значение у такое, что f(xº,y)=1 (т.е предикат истинный),
φ(xº) равно наименьшему среди чисел у таких, что f(xº,y)=1; если же
таких у не существует, то φ(xº) не определено. В этом и заключается
применение μ-оператора к функции f(x,y), символически это
записывается так: φ(x)=μy(f(x,y)=1).
Пример: задан алгоритм Uf, вычисляющий f, т.е распознающий
алгоритм, применимый к парам х||y и выясняющий, имеет ли место
свойство f(x,y)=1. Необходимо найти значения φ(xº) путем проверки
условия Uf для пар хº||0, хº||1, хº||2,.. до тех пор, пока впервые не будет
обнаружено нужное у, в противном случае процесс продолжается сколь
угодно долго. Т.е формула исходного языка: Q°(пока Uf, повторяй E||S),
где Q перерабатывает x в х||0. Она позволяет строить программу Uφ,
если задана Uf. Аналогично обстоит дело, когда μ-оператор
применяется к предикату f(x1,…,xk,y) от любого числа k+1 аргументов,
вычисляя функцию: φ(х1,..., хk)=μy(f(x1,…,xk,y)=1).
Типичной ситуацией применения μ-оператора является построение
обратных функций. Пусть для функции y=f(x) существует обратная
функция, для каждого натурального у существует единственное
значение х, для которого f(x)=y; в таком случае обратная функция
x=φ(y), определяется как φ(y)= μх(f(x)=y).