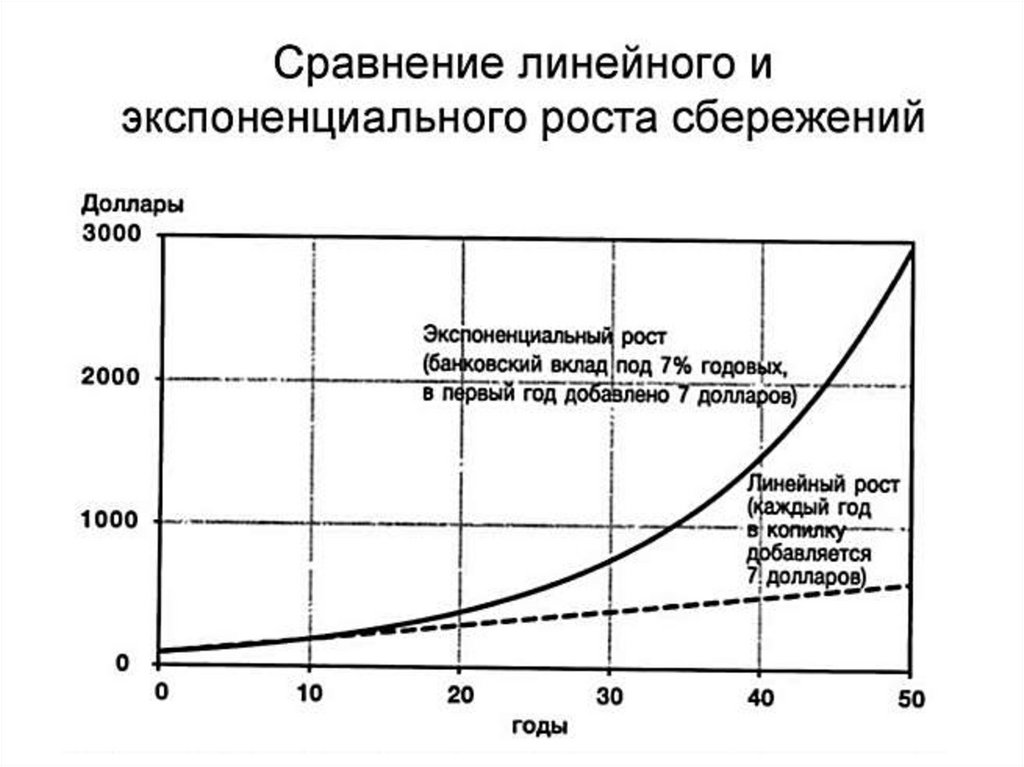
Линейный и экспоненциальный рост

1.

2.

Изображение членов арифметической прогрессии
точками на координатной плоскости
Члены числовой последовательности можно
изображать точками на координатной плоскости.
Для этого по горизонтальной оси откладывают
номер члена, a по вертикальной – соответствующий
член последовательности.
Если последовательность – арифметическая
прогрессия, то точки, изображающие её члены,
лежат на одной прямой. Дело в том, что
зависимость
n–го
члена
арифметической
прогрессии от номера члена n является линейной.
Например, если в арифметической прогрессии
а1 = 1 и d = 3, то аn = 1 + 3(n – 1), т.е. аn = 3n – 2.
Значит, точки, изображающие члены этой прогрессии, лежат на прямой
y = 3x – 2
Изменение членов арифметической прогрессии происходит равномерно: с
каждым шагом по горизонтальной оси изображающие их точки поднимаются
или опускаются на одно и то же число единиц вдоль вертикальной оси.

3. Изображение членов геометрической прогрессии точками на координатной плоскости

Члены числовой последовательности можно
изображать точками на координатной
плоскости.
Для этого по горизонтальной оси откладывают
номер члена, a по вертикальной –
соответствующий член последовательности.
На рисунке точками изображены несколько
членов геометрической прогрессии (bn), в
которой b1 = 1, q = 2; эта прогрессия задаётся
формулой
bn = 2n-1.
Скорость её роста всё время увеличивается, и
точки, соответствующие её членам, резко
«уходят» вверх. Все они лежат на кривой,
которая носит название экспонента. Чем выше
поднимается экспонента у = 2х, тем круче она
становится.

4.

5.

6. ВЫВОД

В рассмотренных случаях
говорится о линейном росте
членов арифметической
прогрессии и об
экспоненциальном росте членов
геометрической прогрессии.

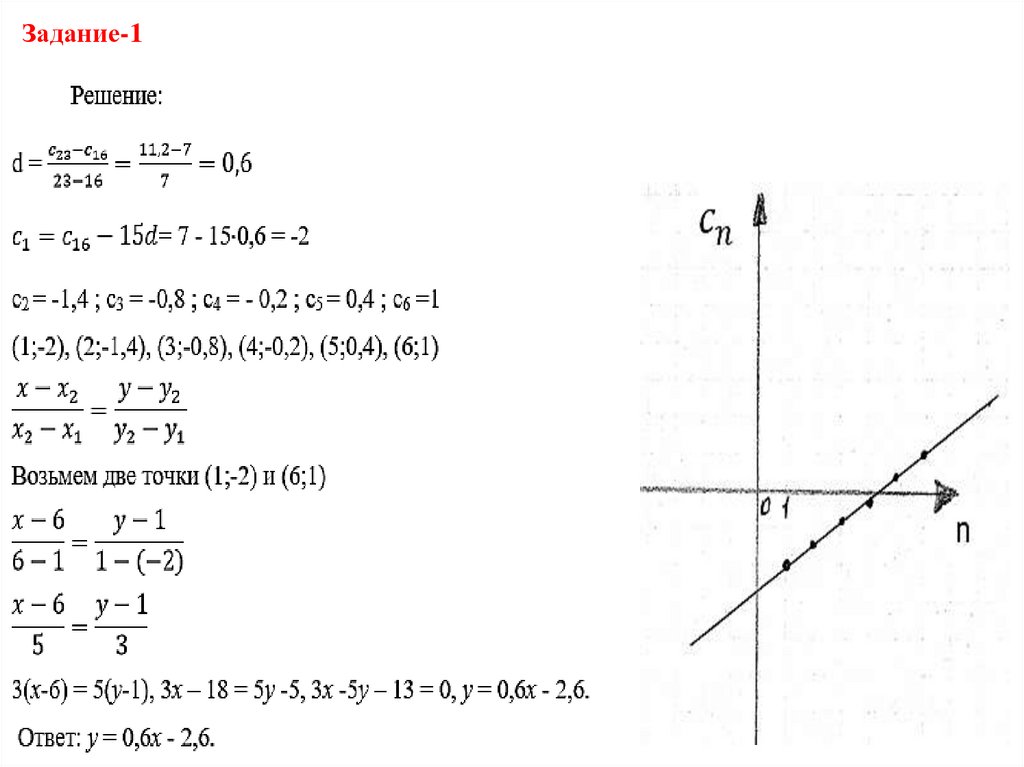
7. Задание-1

Известно, что с16=7, с23=11,2.
Изобразите на координатной плоскости
первые шесть членов арифметической
прогрессии (сn) и напишите уравнение
прямой, на которой лежат построенные
точки.

8.

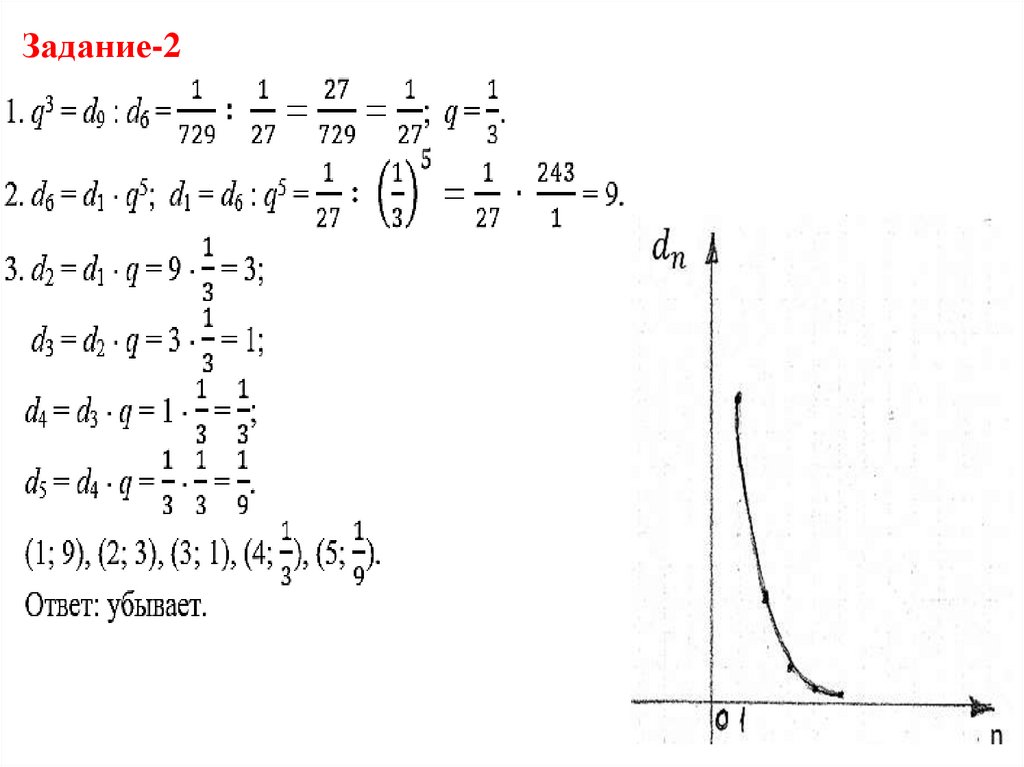
Задание-1

9. Задание-2

Найдите первые пять членов
геометрической прогрессии (dn) и
изобразите их на координатной
плоскости, если известно, что d6=1/27,
d9=1/729.
Определите характер монотонности
функции, на графике которой лежат
построенные точки.

10. Задание-2

11. Задание-3

Члены арифметической
прогрессии изображены
точками на координатной
плоскости. Какое из данных
чисел не удовлетворяет этой
прогрессии?

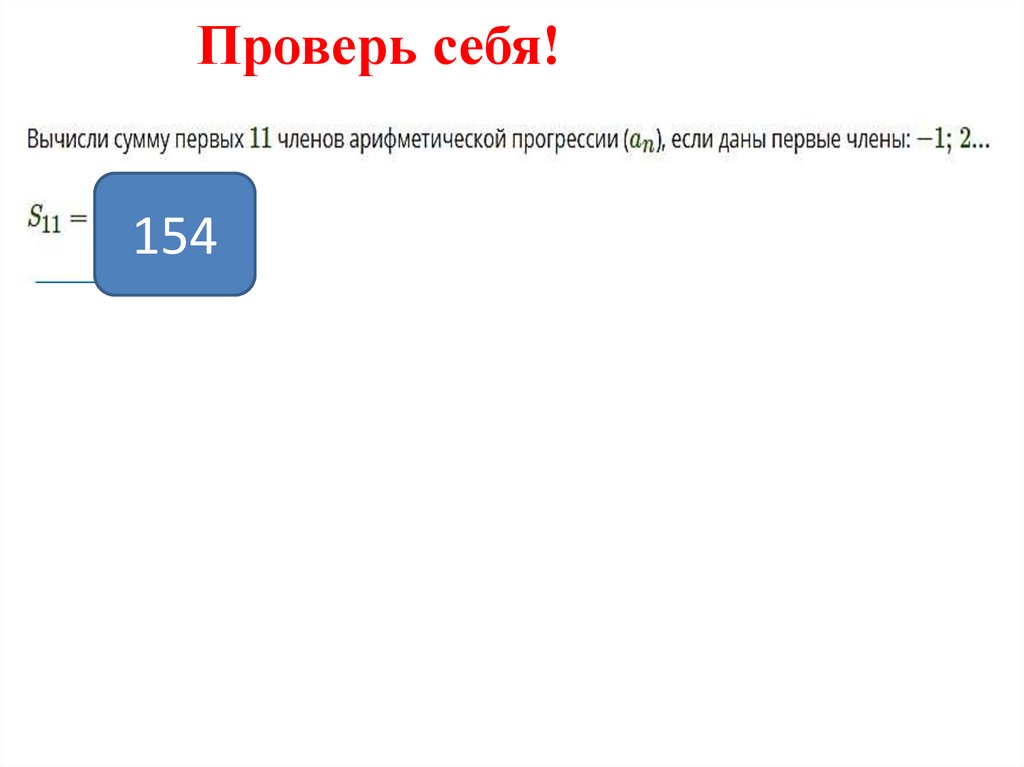
12. Проверь себя!

5,9

13. Проверь себя!

137,6

14. Проверь себя!

154

15. Проверь себя!

16
1
9
729

16. Проверь себя!

2,4
1,2

17. Проверь себя!

-5
4
13
1
7

18. Проверь себя!

-4
-16

19. Проверь себя!

100
2084

20.

Домашнее задание