Математическое ожидание, дисперсия, среднеквадратическое отклонение ДСВ

1.

Дисциплина «ЕН.03 Теория вероятностей и
математическая статистика»
Математическое ожидание,
дисперсия,
среднеквадратическое отклонение
ДСВ

2.

•Две случайные величины называются
независимыми, если закон распределения
одной из них не меняется от того, какие
возможные значения приняла другая величина.
•В противном случае случайные величины
называются зависимыми.

3.

Например,
если имеются билеты двух различных
денежных лотерей, то случайные величины X и
Y, выражающие соответственно выигрыш по
каждому билету (в денежных единицах), будут
независимыми.
Если же случайные величины X и Y выражают
выигрыш по билетам одной денежной лотереи, то в
этом случае X и Y являются зависимыми, ибо любой
выигрыш по одному билету (X = xi) приводит к
изменению вероятностей выигрыша по другому
билету (Y), т.е. к изменению закона распределения Y.

4.

Пусть дана случайная величина Х.
Произведением k∙Х случайной величины X на постоянную
величину k называется случайная величина, которая
принимает значения k∙xi с теми же вероятностями pi (i = 1, 2,
..., n).

5.

6.

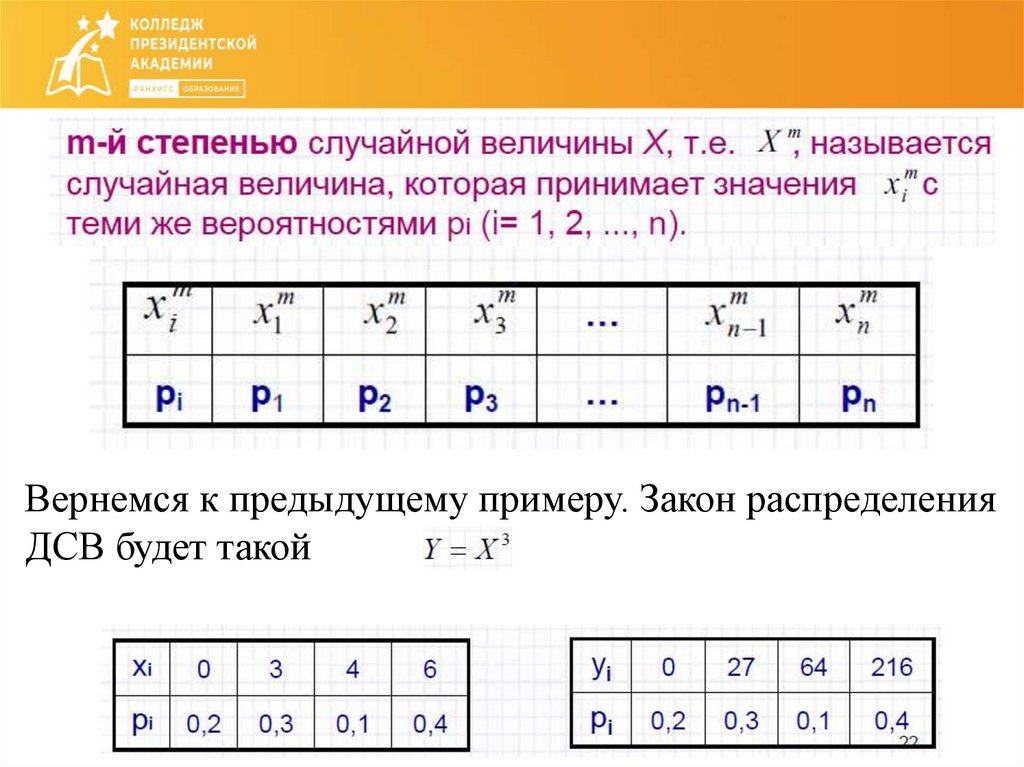
Вернемся к предыдущему примеру. Закон распределения
ДСВ будет такой

7.

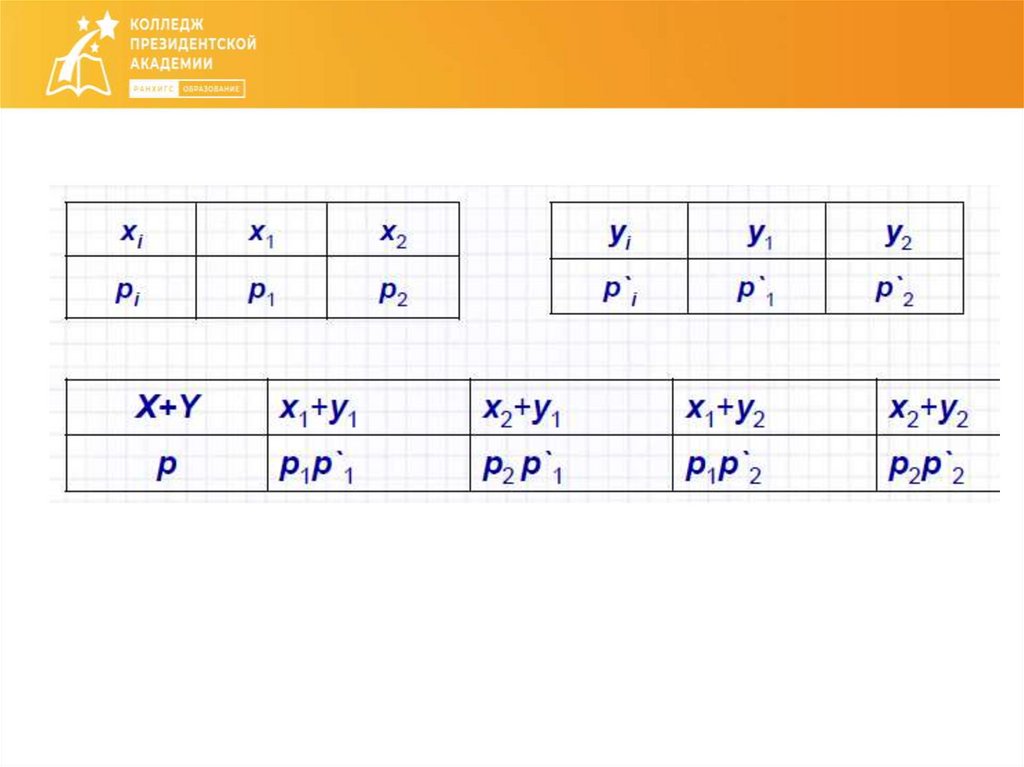
Суммой случайных величин X и Y называется
случайная величина X+Y, возможные значения
которой равны суммам каждого возможного
значения X с каждым возможным значением Y;
вероятности возможных значений X+Y
для независимых величин X и Y равны
произведениям вероятностей слагаемых;
для зависимых величин — произведениям
вероятности одного слагаемого на условную
вероятность второго.

8.

9.

10.

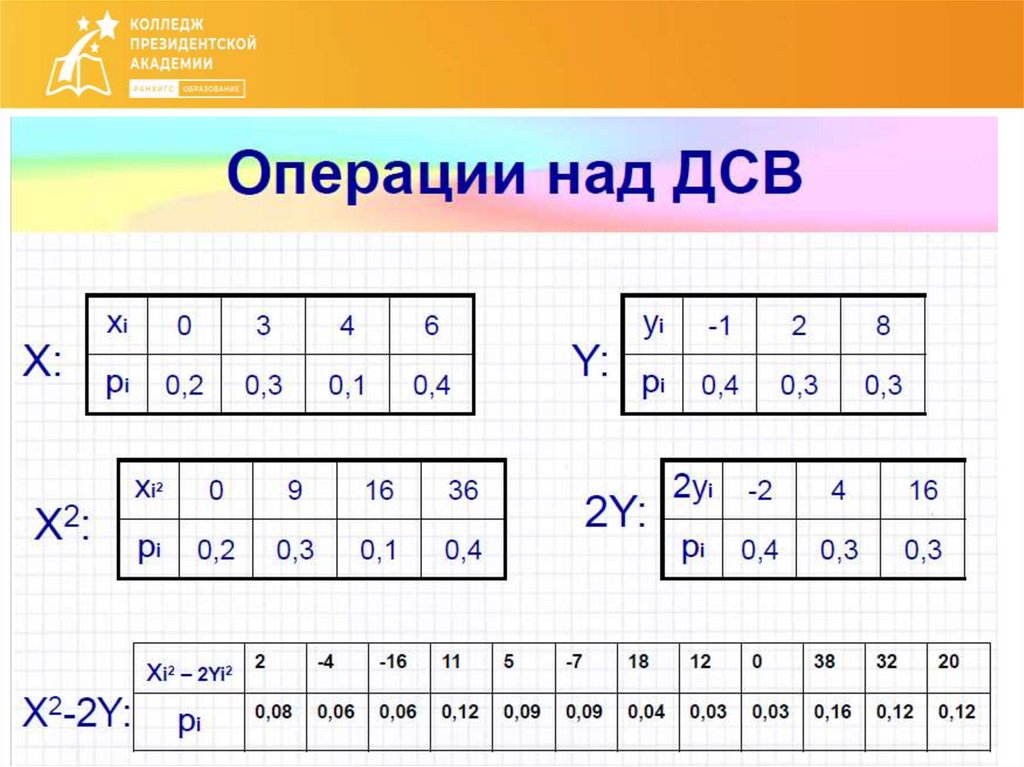
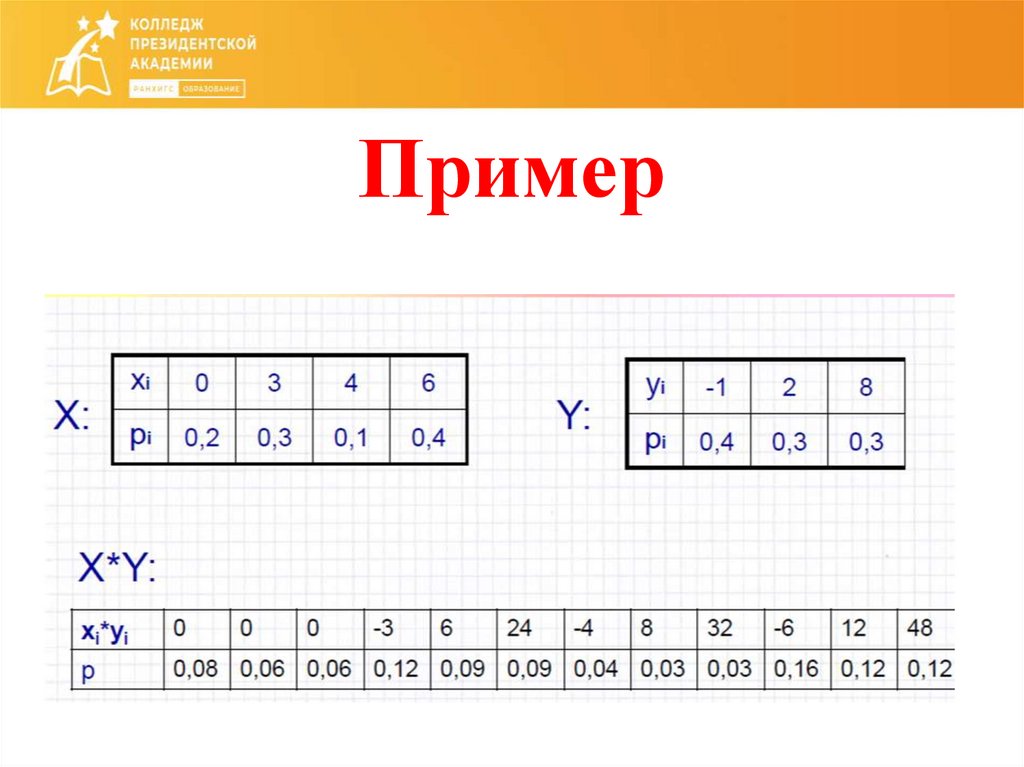
Произведением
независимых случайных величин X и Y
называется случайная величина XY, возможные значения
которой равны произведениям каждого возможного
значения X на каждое возможное значение Y;
вероятности возможных значений произведения XY
равны произведениям вероятностей возможных
значений сомножителей.

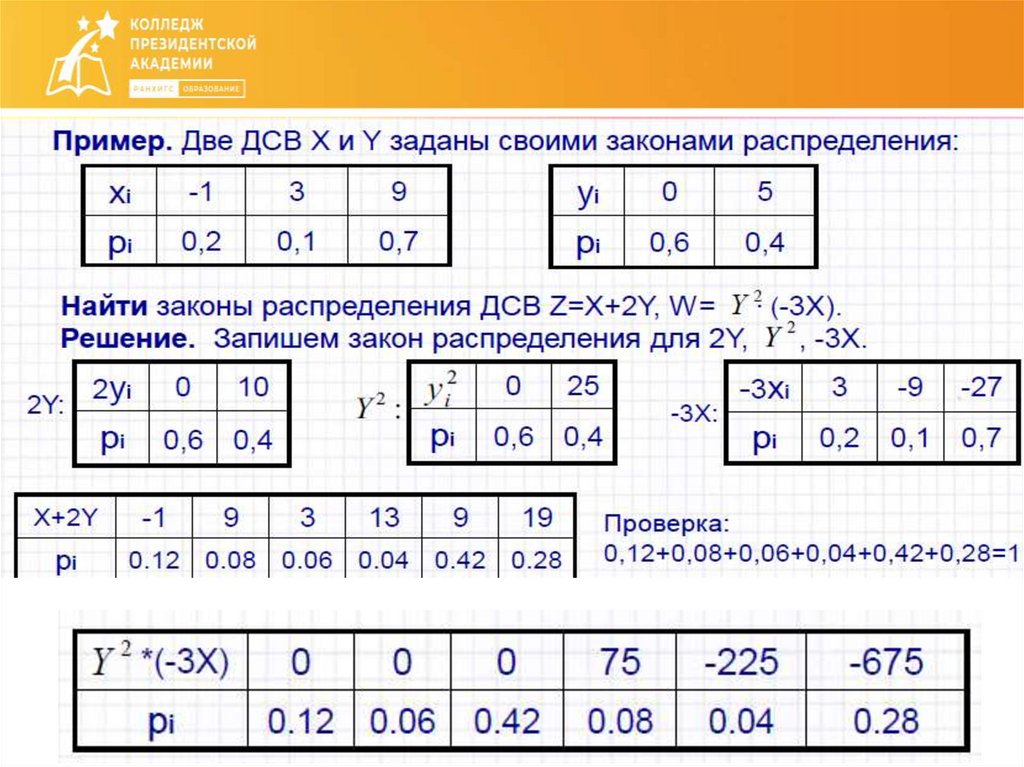
11. Пример

12.

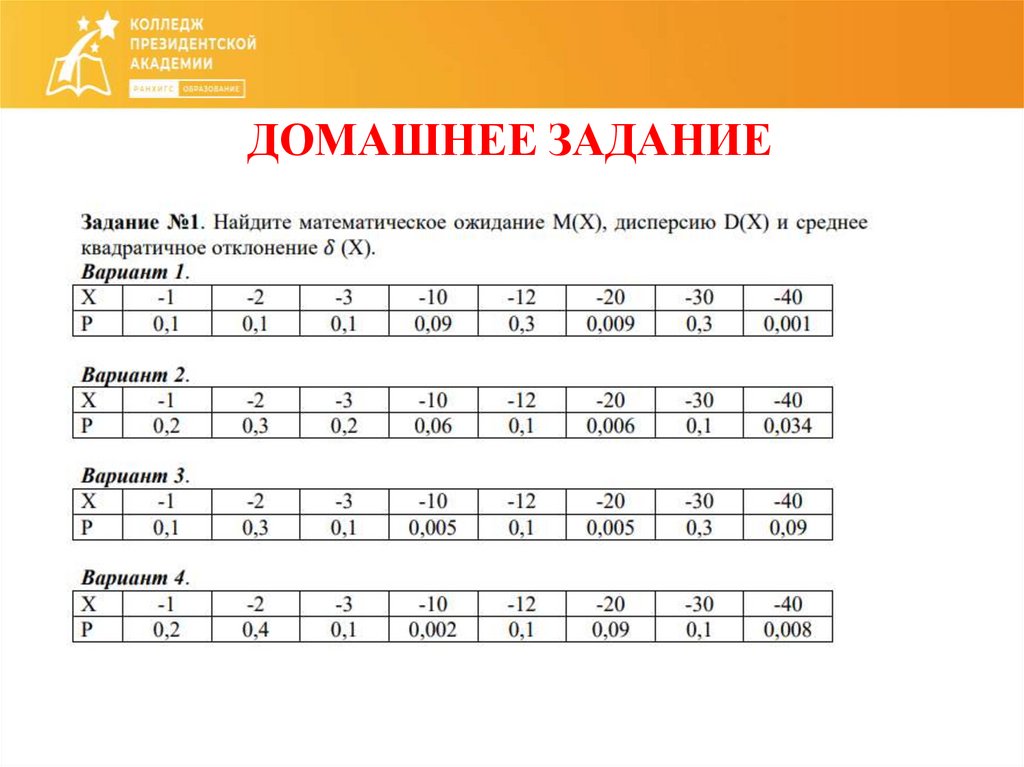
13. Числовые характеристики ДСВ

14.

15. Задача. Известны законы распределения случайных величин Х и Y —числа очков, выбиваемых 1-м и 2-м стрелками.

Необходимо выяснить, какой из двух стрелков стреляет
лучше.

16. РЕШЕНИЕ

Из двух стрелков лучше стреляет тот, кто в среднем выбивает
большее количество очков. Таким средним значением случайной
величины является ее математическое ожидание.
М(Х)=0∙0,15 + 1∙0,11+ 2∙0,04 + 3∙0,05 + 4∙0,04 + 5∙0,1 + 6∙0,1 +
7∙0,04 + 8∙0,05 + 9∙0,12 + 10∙0,2 = 5,36
M(Y)=0∙0,01 + 1∙0,03 + 2∙0,05 + 3∙0,09 + 4∙0,11 + 5∙0,24 + 6∙0,21 +
7∙0,1 + 8 ∙ 0,1+9∙0,04 + 10∙0,02 = 5,36
Среднее число выбиваемых очков у двух стрелков одинаковое

17. Пример. В лотерее разыгрываются: 1 автомобиль стоимостью 5000 ден. ед., 4 телевизора стоимостью по 250 ден. ед., 5 телефонов

стоимостью по 200 ден. ед.
Всего продается 1000 билетов по 7 ден. ед.
Составить закон распределения чистого
выигрыша, полученного участником лотереи,
купившим один билет. Найти математическое
ожидание.

18. Решение. Возможные значения случайной величины X – чистого выигрыша на один билет - равны: 0 - 7 = -7 ден. ед. (если билет не

выиграл),
200 - 7 = 193,
250 - 7 = 243,
5000 - 7 = 4993 ден. ед.
(если на билет выпал выигрыш соответственно телефона,
телевизора или автомобиля).
Учитывая, что из 1000 билетов число не выигравших составляет
990, а указанных выигрышей соответственно 5, 4 и 1, и используя
классическое определение вероятности, получим:
Р(Х=-7) = 990/1000 = 0,990; P(X=193) = 5/1000 = 0,005;
Р(Х=243) = 4/1000 = 0,004; Р(X=4993) = 1/1000 = 0,001.

19. Р(Х=-7) = 990/1000 = 0,990; P(X=193) = 5/1000 =0,005; Р(Х=243) = 4/1000 = 0,004; Р(X=4993) = 1/1000 = 0,001.

Найдем математическое ожидание:
М(Х) = (-7)∙0,990 + 193∙0,005 + 243∙0,004 + 4993∙0,001 = 0,
т.е. средний выигрыш равен нулю.

20.

Свойства математического ожидания:
1. Математическое ожидание постоянной
величины равно самой постоянной: M(С) = С.
2. Постоянный множитель можно выносить за знак
математического ожидания, т.е. М(kХ) = kМ(Х).
3. Математическое ожидание алгебраической
суммы конечного числа случайных величин равно
сумме их математических ожиданий, т.е.
М(Х± Y) = М(Х) ± M(Y)

21. 4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических

ожиданий
M(XY) = M(X)∙M(Y).

22. Пример. Найти математическое ожидание случайной величины Z= 8Х- 5XY+ 7, если известно, что М(Х) = 3, M(Y)= 2.

23. РЕШЕНИЕ

Используя свойства 1, 2, 3, 4 математического
ожидания, найдем
M(Z)= M(8Х - 5XY+ 7)= M(8X) – M(5XY) + M(7)= 8M(X) –
5M(X)∙M(Y) +7 = 8∙3 - 5∙3∙2 +7 = 24 – 30 + 7 = 1
Ответ: математическое ожидание случайной величины Z
равно 1.

24. Пример. В результате обработки данных многолетних наблюдений получены распределения случайных величин Х и Y – числа хозяйств в

каждом из двух районов
области, в которых урожайность яровых
зерновых культур может превысить 35 ц/га.

25. Найти математическое ожидание M(Z) случайной величины Z=X+Y двумя способами: 1. исходя из закона распределения Z; 2. используя

свойства математического ожидания.
Убедиться в том, что в условиях данной задачи
эти свойства
матожидания независимых случайных величин
выполняются

26. РЕШЕНИЕ.

1) Найдем закон распределения ДСВ Z=X+Y:
M(Z) = 1∙0.02 + 2∙0.2 +3∙0.54 + 4∙0.24 = 3
2) Вычислим матожидание ДСВ Z=X+Y, используя свойства.
Найдем M(X) и M(Y):
M(X) = 1∙0.1 + 2∙0.6 + 3∙0.3= 2.2
M(Y) = 0∙0.2 + 1∙0.8 = 0.8
M(Z) = M(X+Y) = M(X) + M(Y) = 2.2 + 0.8 =3.

27.

Сравнив значение M(Z), полученное в пункте
1) и в пункте 2),
убеждаемся в том, что матожидания Z,
найденные двумя различными способами,
совпадают.

28.

Математические ожидания обеих величин одинаковы, а
возможные значения различны,
причем X имеет возможные значения, близкие к
математическому ожиданию,
а У - далекие от своего математического ожидания.

29.

Для того чтобы оценить, как рассеяны
возможные значения случайной величины
вокруг ее математического ожидания,
пользуются, в частности, числовой
характеристикой, которую называют
дисперсией

30. Пусть X - случайная величина и М (X) – ее математическое ожидание. Рассмотрим в качестве новой случайной величины разность X -

М(Х).
Отклонением называют разность между
случайной величиной и ее математическим
ожиданием.

31. Пусть закон распределения X известен:

Найдем закон распределения отклонения:
X - М(Х):

32. Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины

от ее
математического ожидания:
D(X) = M (X – M(X))².

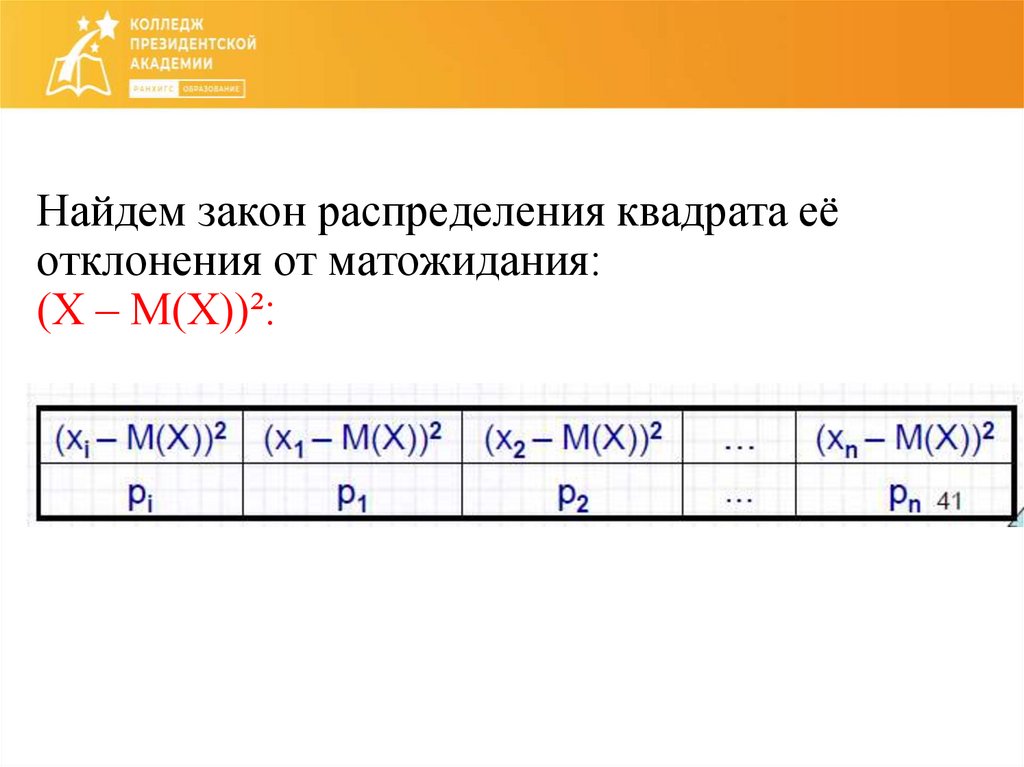
33. Найдем закон распределения квадрата её отклонения от матожидания: (Х – M(X))²:

34.

35. Формула для вычисления дисперсии. Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и

квадратом ее
математического ожидания:

36. Пример. Найти дисперсию случайной величины X, которая задана следующим законом распределения:

Найдем математическое ожидание М (X):
М (Х) = 2 ∙ 0,1+3 ∙ 0,6 + 5 ∙ 0,3 = 3,5.
Найдем математические ожидания М (Х2):
М(Х²) = 4 ∙ 0,1 +9 ∙ 0,6 + 25 ∙ 0,3= 13,3.
Искомая дисперсия:
D(X)= M (X²)—[М (Х)]² = 13,3 – (3,5)² =1,05.
Х: Х²:

37. Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:

38.

Пример.
Найти среднее квадратическое отклонение ДСВ Х, заданной
законом распределения.
Вычислим М(Х) и М(Х²):
М(Х) = 1∙0,2 + 3∙0,6 + 6∙0,2 = 3,2.
М(Х²): = 1∙0,2 + 9∙0,6 + 36∙0,2 = 12,8.
D(X) = М(Х²):– [М(Х)]² = 12.8 – 3.2² = 12.8 – 10,24 = 2,56.

39. Свойства дисперсии: 1. Дисперсия постоянной величины С равна нулю: D (С) = 0. 2. Постоянный множитель можно выносить за знак

дисперсии, возводя его в квадрат:
D(kX) = k²D(X).
3. Дисперсия суммы двух независимых случайных
величин равна сумме дисперсий этих величин:
D(X + Y) = D(X) + D(Y).
4. Дисперсия разности двух независимых случайных
величин равна сумме их дисперсий:
D(X - Y) = D(X) + D(Y).

40.

Пример.
Даны две ДСВ X и Y:
Найти
матожидание и дисперсию ДСВ Z =Y-X двумя способами:
1) Исходя из закона распределения Z;
2) Используя свойства матожидания и дисперсии.

41. РЕШЕНИЕ

1)Составим закон распределения Z:

42.

Сравнив значение M(Z) и D(Z), полученные в пункте 1) и 2),
убеждаемся в том, что числовые характеристики Z, найденные
двумя различными способами, совпадают

43. ДОМАШНЕЕ ЗАДАНИЕ