Графы решение задач 7 класс Подготовка к ВПР

1.

Графы
решение задач
7 класс
Подготовка к ВПР

2.

Основные понятия
Эйлеров цикл — это цикл, который проходит по
каждому ребру графа ровно один раз и
возвращается в исходную вершину.
Полуэйлеров цикл — это путь, который проходит
по каждому ребру графа ровно один раз, но не
обязательно возвращается в исходную вершину.
Если граф не содержит эйлерова цикла, то для
обхода всех рёбер необходимо пройти некоторые
рёбра дважды.

3.

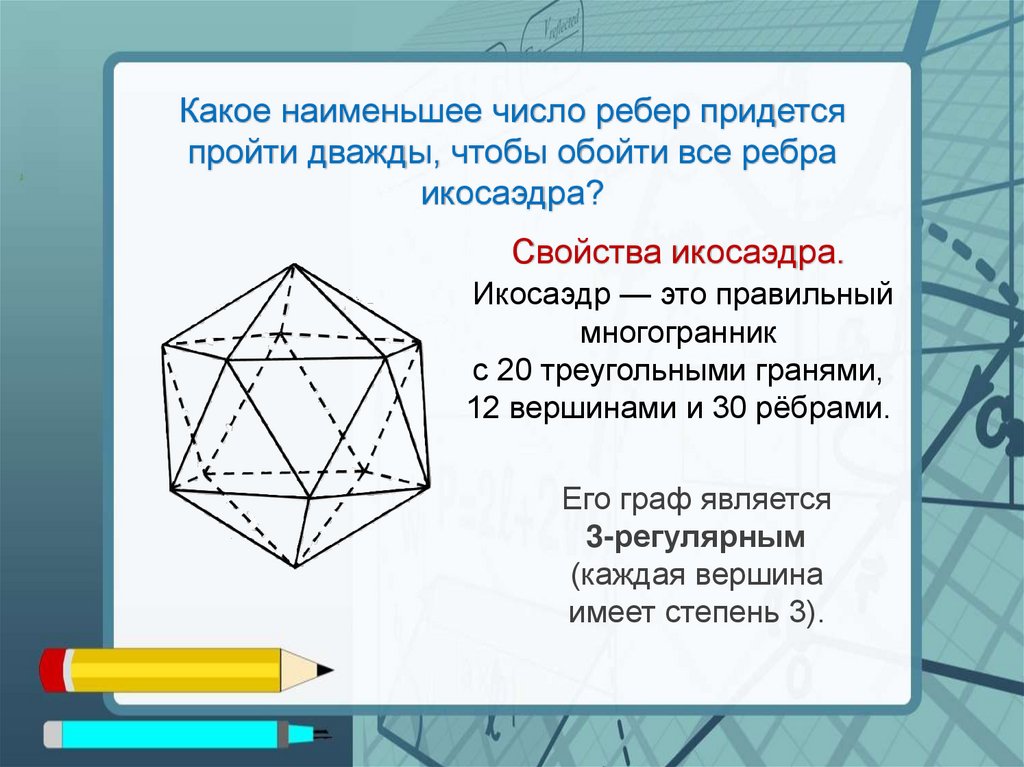
Какое наименьшее число ребер придется
пройти дважды, чтобы обойти все ребра
икосаэдра и вернуться в исходную вершину?
Свойства икосаэдра.
Икосаэдр — это правильный
многогранник
с 20 треугольными гранями,
12 вершинами и 30 рёбрами.
Его граф является
3-регулярным
(каждая вершина
имеет степень 3).

4.

Решение:
Для того чтобы граф имел эйлеров цикл,
необходимо и достаточно, чтобы:
• Граф был связным.
• Все вершины имели чётную степень.
В случае икосаэдра:
• Граф связный.
• Все вершины имеют степень 3 (нечётную).
Таким образом, икосаэдр не имеет эйлерова
цикла.

5.

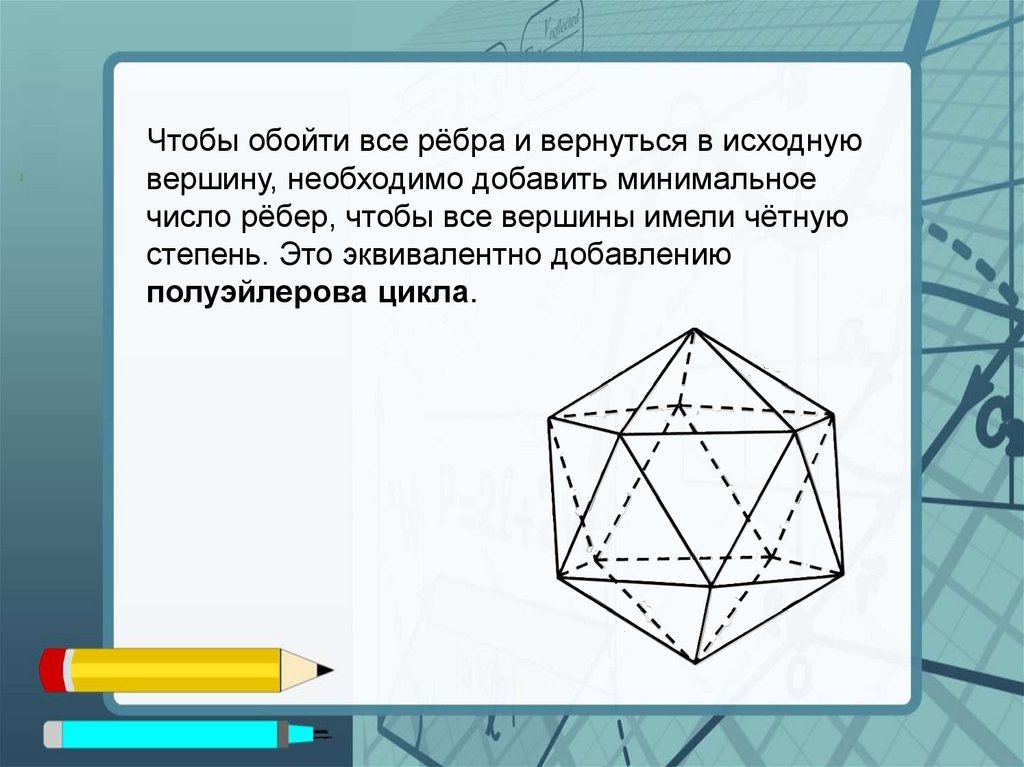
Чтобы обойти все рёбра и вернуться в исходную
вершину, необходимо добавить минимальное
число рёбер, чтобы все вершины имели чётную
степень. Это эквивалентно добавлению
полуэйлерова цикла.

6.

Для икосаэдра:
• Число вершин с нечётной степенью: 12
(все вершины имеют степень 3).
• Чтобы сделать все степени чётными, нужно
добавить рёбра, соединяющие вершины с
нечётными степенями.
Минимальное число таких рёбер равно
половине числа вершин с нечётными
степенями: 12 : 2 = 6
Однако, поскольку мы добавляем рёбра для
создания эйлерова цикла, каждое добавленное
ребро будет пройдено дважды.
Таким образом, минимальное число рёбер,
которые нужно пройти дважды, равно 6.
Ответ : 6 ребер

7.

Какое наименьшее число ребер придется
пройти дважды, чтобы обойти все ребра
икосаэдра?
Свойства икосаэдра.
Икосаэдр — это правильный
многогранник
с 20 треугольными гранями,
12 вершинами и 30 рёбрами.
Его граф является
3-регулярным
(каждая вершина
имеет степень 3).

8.

Решение:
• В икосаэдре каждая вершина имеет степень 3
(нечётную).
• Количество вершин с нечётной степенью — 12.
• Чтобы сделать возможным эйлеров путь, нужно
уменьшить количество вершин с нечётной
степенью до 2.
• Для этого необходимо добавить рёбра (или
пройти существующие рёбра дважды), чтобы
"соединить" пары вершин с нечётными
степенями.
• Минимальное количество таких добавленных
рёбер равно (12−2) : 2 = 5.
Ответ : 5 ребер

9.

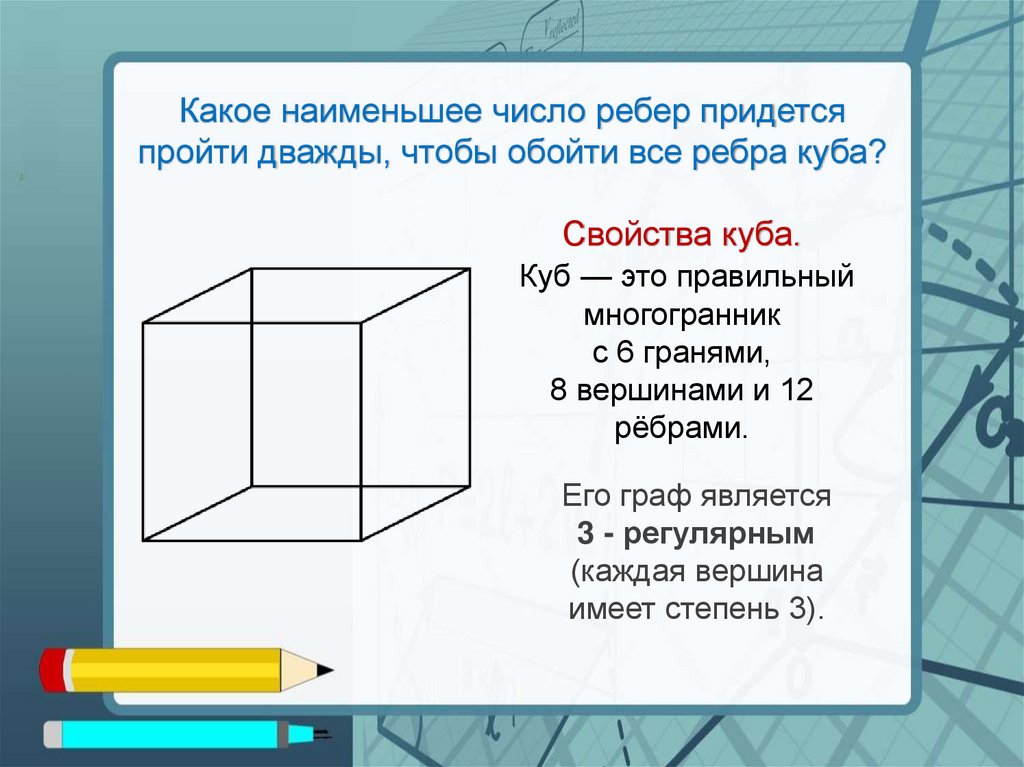
Какое наименьшее число ребер придется
пройти дважды, чтобы обойти все ребра куба?
Свойства куба.
Куб — это правильный
многогранник
с 6 гранями,
8 вершинами и 12
рёбрами.
Его граф является
3 - регулярным
(каждая вершина
имеет степень 3).

10.

Решение:
• Чтобы сделать граф эйлеровым, необходимо
добавить рёбра (или пройти существующие
дважды) так, чтобы только 2 вершины имели
нечётную степень.
• Для этого нужно уменьшить количество
вершин с нечётной степенью с 8 до 2.
• Каждое добавленное ребро (или проход по
существующему дважды) изменяет степени двух
вершин: если они были нечётными, становятся
чётными, и наоборот.
• Чтобы изменить степени 6 вершин (с нечётной
на чётную), потребуется 3 дополнительных
ребра.
Ответ: 3 ребра

11.

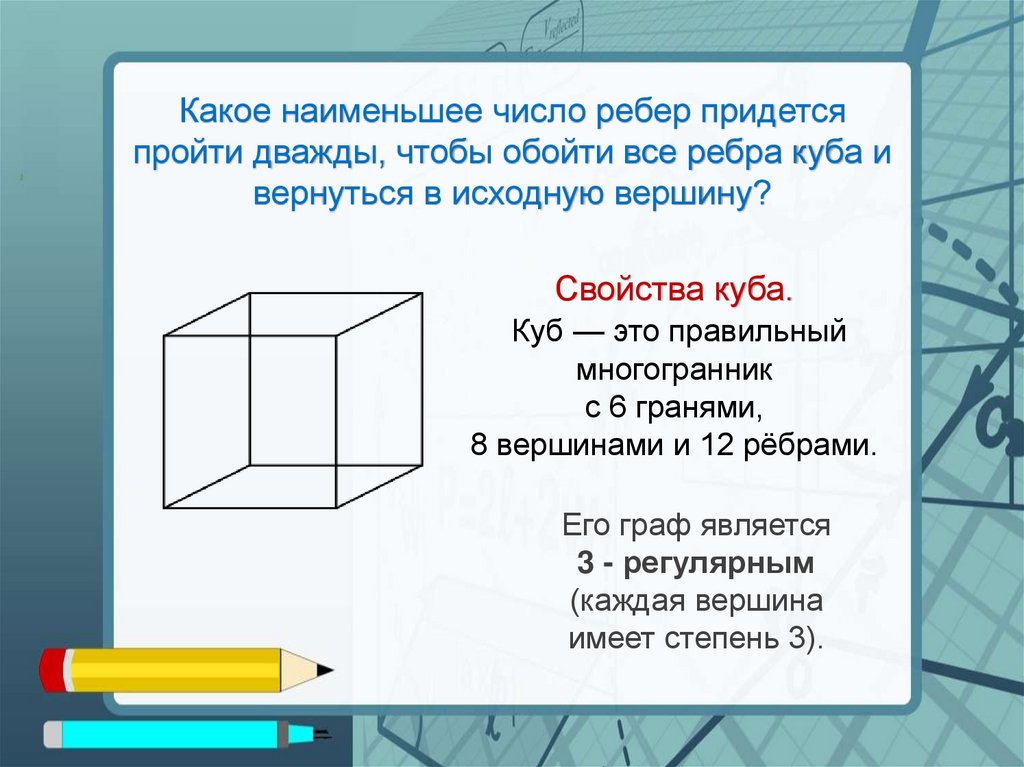
Какое наименьшее число ребер придется
пройти дважды, чтобы обойти все ребра куба и
вернуться в исходную вершину?
Свойства куба.
Куб — это правильный
многогранник
с 6 гранями,
8 вершинами и 12 рёбрами.
Его граф является
3 - регулярным
(каждая вершина
имеет степень 3).

12.

Решение:
В кубе все вершины имеют степень 3 (нечётную),
что означает, что эйлеров цикл невозможен без
повторения некоторых рёбер.
Чтобы сделать все вершины чётными, нужно
добавить рёбра, которые будут пройдены
дважды.
Каждое добавленное ребро изменяет степени
двух вершин на 1 (делая их чётными).
Для куба с 8 вершинами нечётной степени
потребуется как минимум 8 : 2 = 4 рёбер, чтобы
сделать все степени чётными.
Ответ: 4 ребра

13.

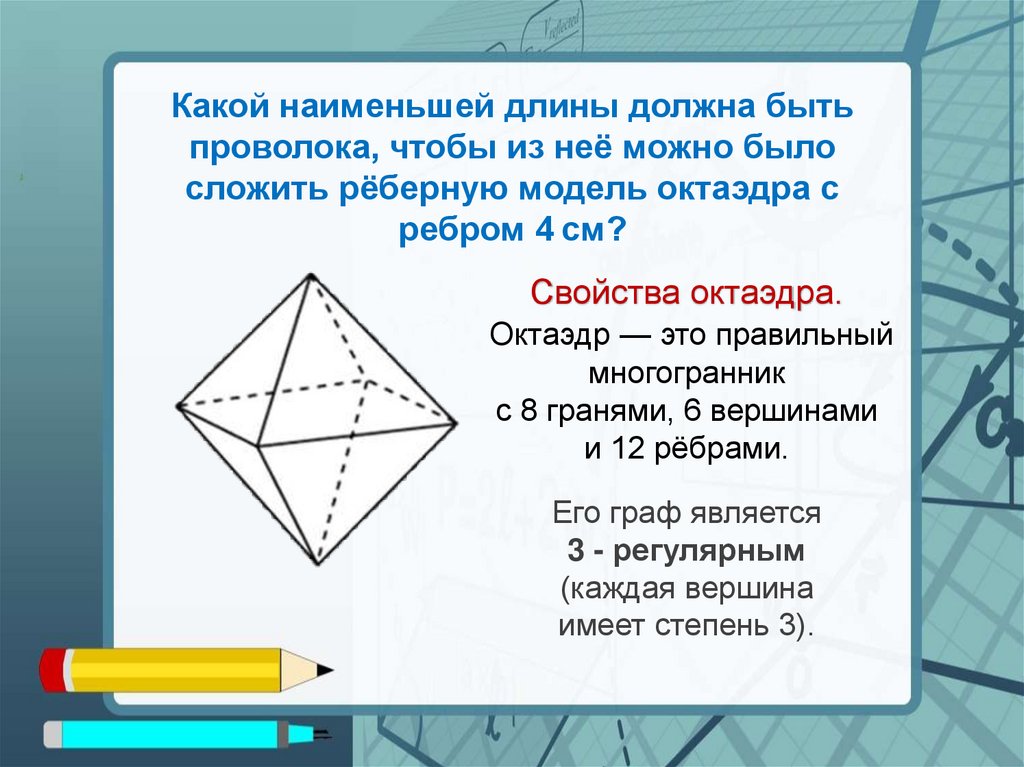
Какой наименьшей длины должна быть
проволока, чтобы из неё можно было
сложить рёберную модель октаэдра с
ребром 4 см?
Свойства октаэдра.
Октаэдр — это правильный
многогранник
с 8 гранями, 6 вершинами
и 12 рёбрами.
Его граф является
3 - регулярным
(каждая вершина
имеет степень 3).

14.

Решение:
В октаэдре каждая вершина соединена с 4 другими
вершинами (степень каждой вершины равна 4).
Таким образом:
Все вершины имеют чётную степень (степень 4).
Следовательно, в графе октаэдра
существует эйлеров цикл — замкнутый путь,
который проходит по каждому ребру ровно один
раз и возвращается в начальную вершину.
Граф связный. Длина одного ребра: 4 см.
Количество рёбер: 12.
Общая длина проволоки вычисляется по
формуле:
L = количество рёбер × длина одного ребра
12 × 4 = 48 см
Ответ: 48 см

15.

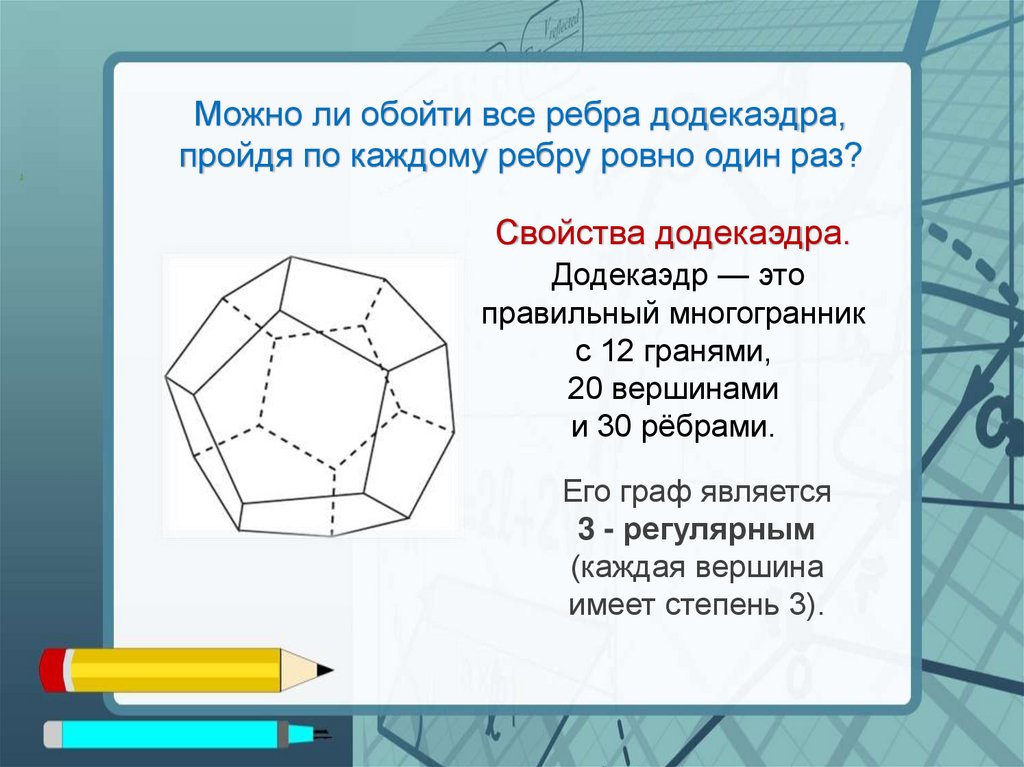
Можно ли обойти все ребра додекаэдра,
пройдя по каждому ребру ровно один раз?
Свойства додекаэдра.
Додекаэдр — это
правильный многогранник
с 12 гранями,
20 вершинами
и 30 рёбрами.
Его граф является
3 - регулярным
(каждая вершина
имеет степень 3).

16.

Решение:
В додекаэдре каждая вершина имеет степень 5
(так как каждая вершина соединена с 5 другими
вершинами).
Поскольку степень каждой вершины нечетная, в
додекаэдре все 20 вершин имеют нечетную
степень.
Поскольку в додекаэдре более двух вершин
имеют нечетную степень, эйлеров путь (и тем
более эйлеров цикл) в нем невозможен. Таким
образом, обойти все ребра додекаэдра, пройдя по
каждому ребру ровно один раз, нельзя.