Similar presentations:
Элементы математической статистики
1. Элементы математической статистики
Задача математической статистики – состоит всоздании
методов
сбора
и
обработки
статистических данных для получения научных и
практических выводов
2. Генеральная и выборочная совокупности
• Выборочной совокупностью или просто выборкойназывается совокупность случайно отобранных объектов.
• Генеральной совокупностью называют совокупность
объектов, из которых производится выборка.
• Объемом совокупности (выборочной или генеральной)
называют число объектов этой совокупности.
Пример:
Из 100 000 жителей города «А», отобрано для исследования
1000 жителей.
Генеральная совокупность – жители города «А»,
объем генеральной совокупности N=100 000,
а объем выборки n=1000.
3. Повторная и бесповторная выборки. Репрезентативная выборка.
При составлении выборки можно поступать двумя способами: послетого как объект отобран и над ним произведено наблюдение, он
может быть возвращен либо не возвращен в генеральную
совокупность.
Повторной называют выборку, при которой отобранный
объект (перед отбором следующего) возвращают в
генеральную совокупность.
Бесповторной называют выборку, при которой не
возвращают.
Для того чтобы по данным выборки можно было достаточно уверенно
судить об интересующем признаке генеральной совокупности,
необходимо, чтобы объекты выборки правильно его представляли
(правильная пропорция генеральной совокупности). Это
требование коротко формулирую т:
«Выборка должна быть Репрезентативной»
4. Способы отбора
На практике применяются различные способы отбора. Принципиальноэти способы можно разделить на два вида:
• Отбор, не требующий расчленения генеральной
совокупности на части. Сюда относятся: а) простой
случайный бесповторный отбор; б) простой случайный
повторный отбор.
• Отбор,
при
котором
генеральная
совокупность
разбивается на части. Сюда относятся: а) типический
отбор; б) механический отбор; в) серийный отбор.
5. Способы отбора
• Простым случайным называют такой отбор, при которомобъекты извлекают по одному из всей генеральной
совокупности (если возвращаем – повторный, если нет бесповторный).
• Типическим называют отбор, при котором объекты отбираются
не из всей генеральной совокупности, а из каждой ее
«типической» части.
• Механическим называют отбор, при котором генеральную
совокупность «механически» делят на столько групп, сколько
объектов должно войти в выборку, а из каждой группы
отбирают один объект.
• Серийным называют отбор, при котором объекты отбирают из
генеральной совокупности не по одному а «сериями», которые
подвергаются сплошному обследованию.
На практике часто применяют комбинированный отбор. Например генеральную
совокупность разбивают на серии одинакового объема и из каждой серии простым
случайным отбором извлекают отдельные объекты
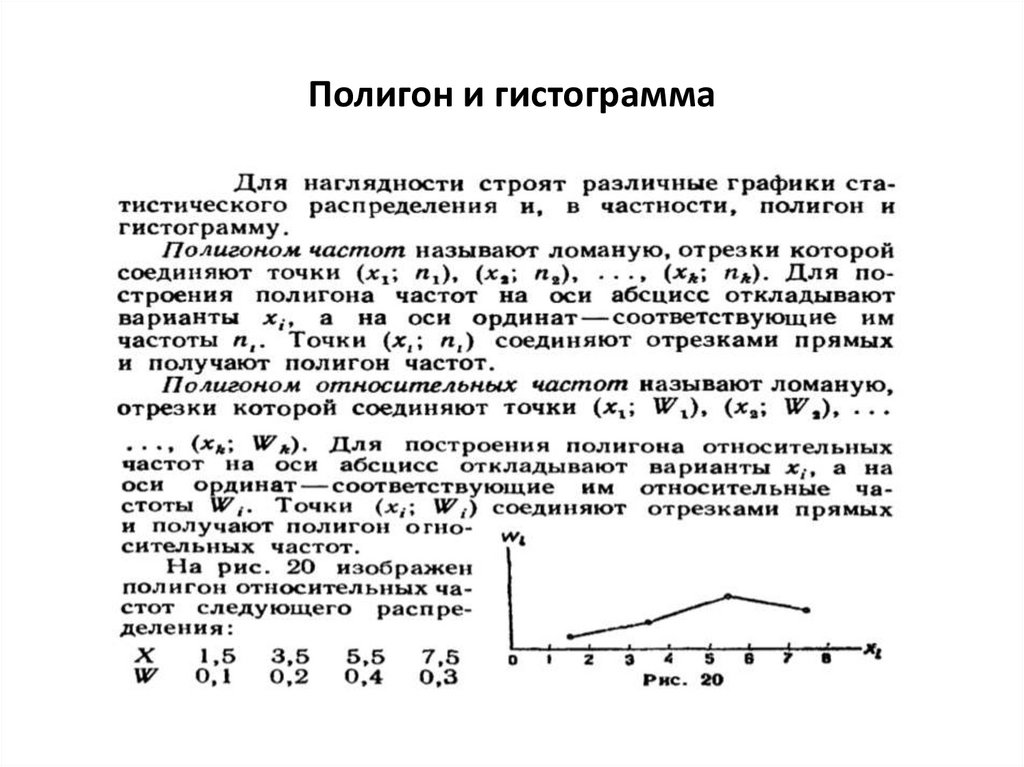
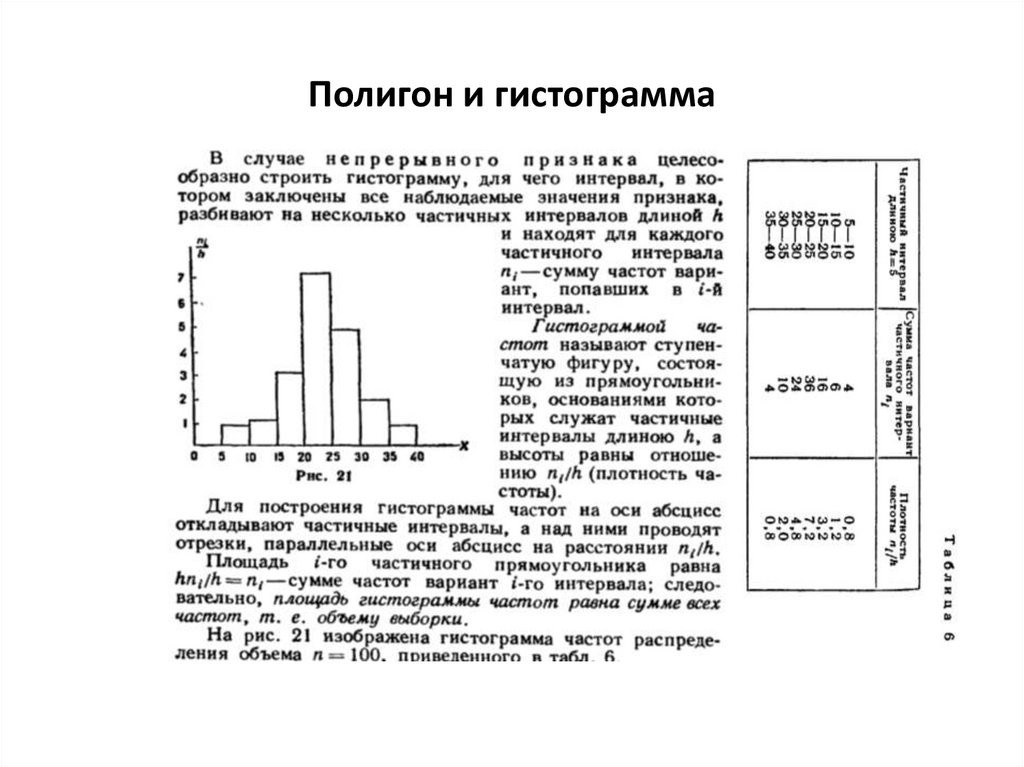
6. Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка,причем х1 наблюдалось n1 раз, х2 – n2 раз, …, хк – nk раз и
n1+n2+…+nk=n – объем выборки.
Наблюдаемые значения хi называют вариантами, а
последовательность вариант, записанных в возрастающем
порядке – вариационным рядом.
Числа ni называют частотами, а их отношение к объему
выборки (ni/n=wi) - относительными частотами.
Статистическим распределением выборки называют
перечень вариант и соответствующих им частот
(относительных частот)
7. Статистическое распределение выборки
8. Эмпирическая функция распределения
Пусть известно статистическое распределение частот количественногопризнака Х. Введем обозначение nx - число наблюдений, при котором
наблюдалось значение признака, меньшее х; n – общее число
наблюдений (объем выборки). Тогда относительная частота события
X<x равна nx/n. Если меняется х, то меняется относительная частота.
Относительную частоту nx/n рассматриваем как функцию зависящую
от х. Так как эта функция находится эмпирически (опытным) путем,
то ее называют эмпирической.
Эмпирической функцией распределения (функцией распределения
выборки) называют функцию F*(x), определяющую для каждого
значения х относительную частоту X<x.
F*(x)= nx/n
где nx число вариант, меньших х; n – объем выборки.
Функцию распределения F(x) генеральной совокупности называют
теоретической функцией распределения.
9. Эмпирическая функция распределения
Различие между эмпирической и теоретической функциямисостоит в том, что теоретическая функция F(x) определяет
вероятность события X<x, а эмпирическая функция F*(x)
определяет относительную частоту этого события.
Из теоремы Бернулли следует, что относительная частота
события X<x: F*(x) стремится по вероятности к F(x).
Другими словами, при больших n (объем выборки) F*(x) и
F(x) мало чем отличаются.
Lim P(|F(x)-F*(x)|<t)=1 (t>0)
Отсюда следует, что целесообразнее использовать эмпирическую функцию
распределения выборки для приближенного представления
теоретической функции распределения генеральной совокупности
10. Эмпирическая функция распределения
Свойства эмпирической функции распределения1. Значения эмпирической функции принадлежат отрезку
[0,1];
2. F*(x) – неубывающая функция;
3. Если х1 наименьшая варианта, то F*(x) =0 при х≤ х1 ;
если хк – наибольшая варианта, то F*(x) =1 при х> хк













 mathematics
mathematics








