Графическое изображение множеств на диаграммах Эйлера-Венна. Решение логических задач

1. РАЗДЕЛ 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ Тема 2.3. Графическое изображение множеств на диаграммах Эйлера-Венна. Решение логических

задач.
Диаграмма Эйлера-Венна — геометрическая схема,
которая используется для моделирования множеств и
для схематичного изображения и отношений между
ними. Диаграмма позволяет наглядно отразить
различные утверждения о множествах.
Диаграммы нашли свое применение в математике,
логике,
менеджменте
и
других
прикладных
направлениях.

2.

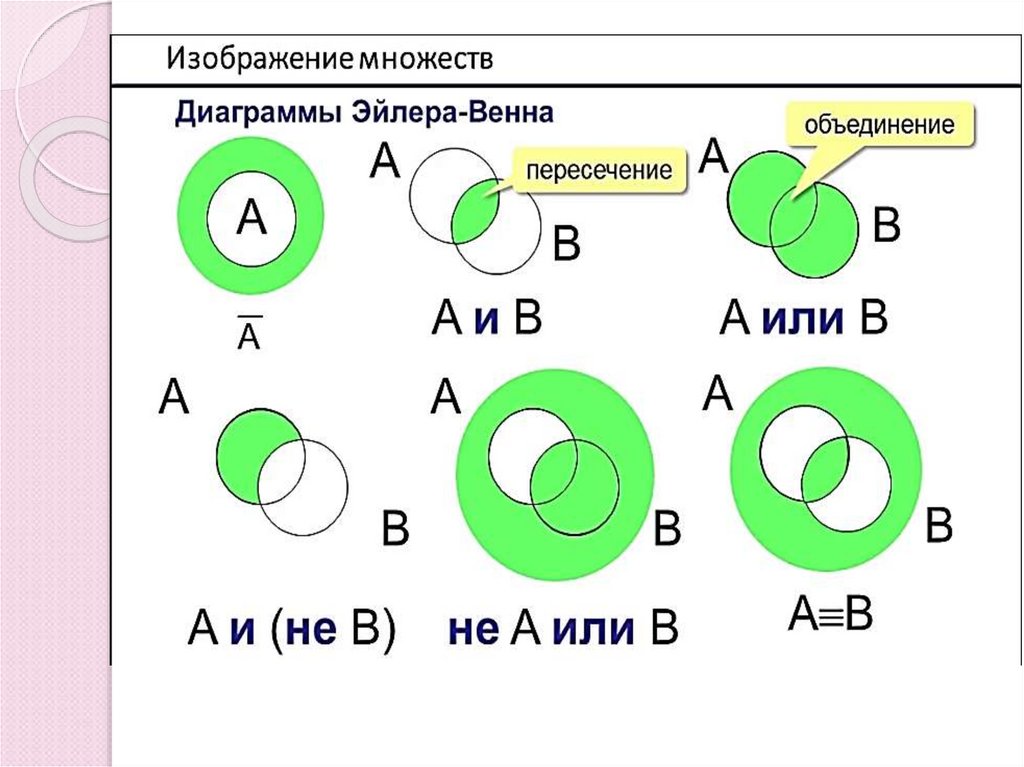
Диаграмма Эйлера-Венна
— схематичное изображение
всех возможных отношений
(объединение, пересечение,
разность,
симметрическая
разность) нескольких (часто
—
трёх)
подмножеств
универсального множества.
На диаграммах Венна
универсальное множество U
изображается множеством
точек
некоторого
прямоугольника, в котором
располагаются
в
виде
кругов или других простых
фигур
все
остальные
рассматриваемые
множества.

3.

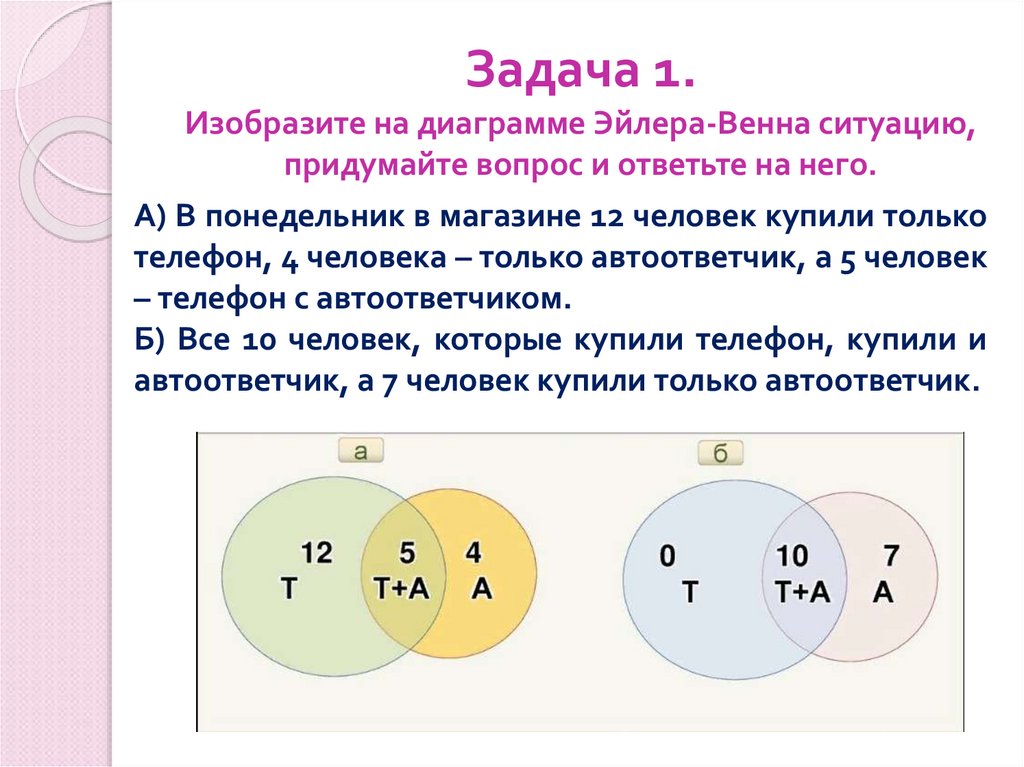
4. Задача 1. Изобразите на диаграмме Эйлера-Венна ситуацию, придумайте вопрос и ответьте на него.

А) В понедельник в магазине 12 человек купили только
телефон, 4 человека – только автоответчик, а 5 человек
– телефон с автоответчиком.
Б) Все 10 человек, которые купили телефон, купили и
автоответчик, а 7 человек купили только автоответчик.

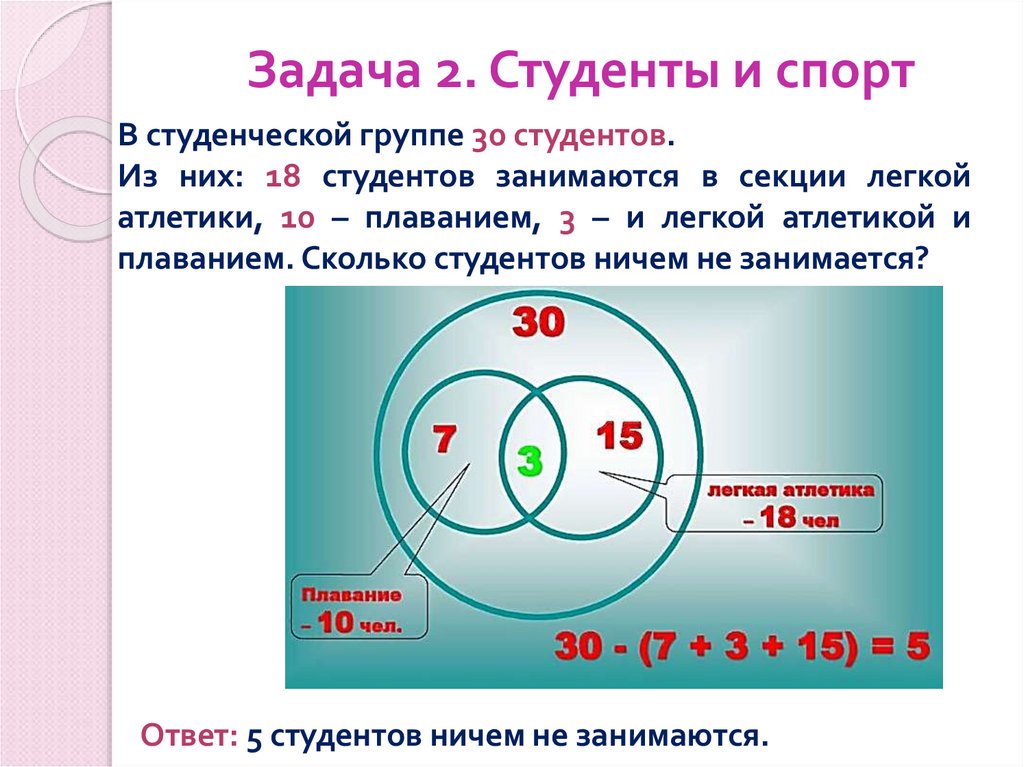
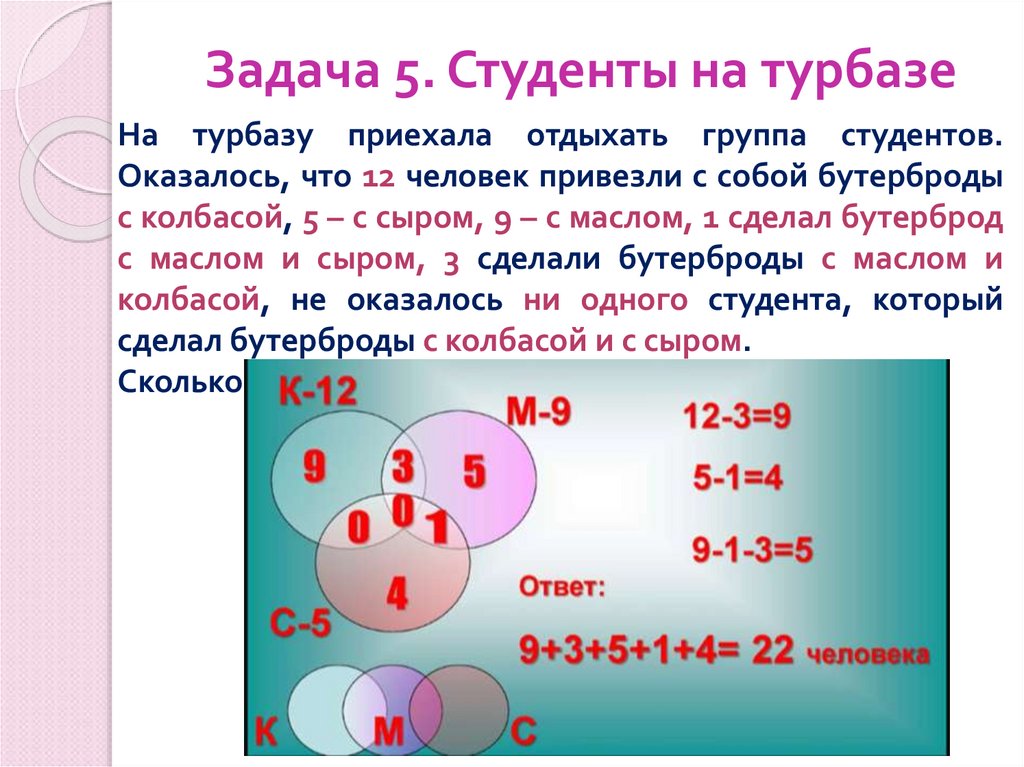
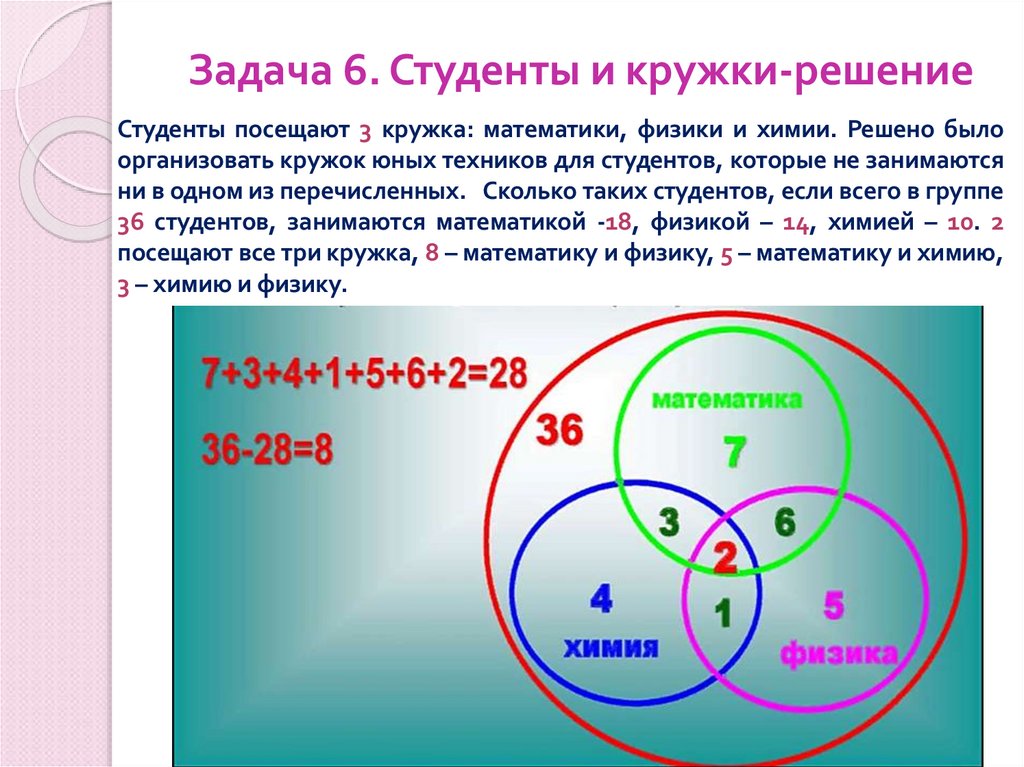
5. Задача 2. Студенты и спорт

В студенческой группе 30 студентов.
Из них: 18 студентов занимаются в секции легкой
атлетики, 10 – плаванием, 3 – и легкой атлетикой и
плаванием. Сколько студентов ничем не занимается?
Ответ: 5 студентов ничем не занимаются.

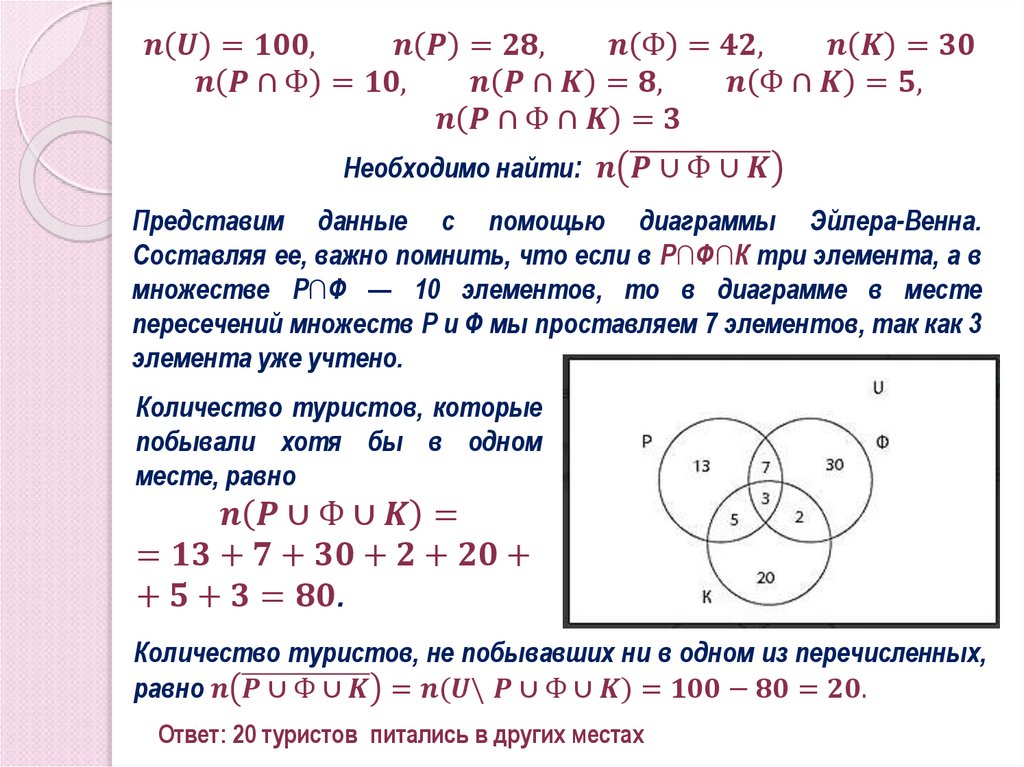
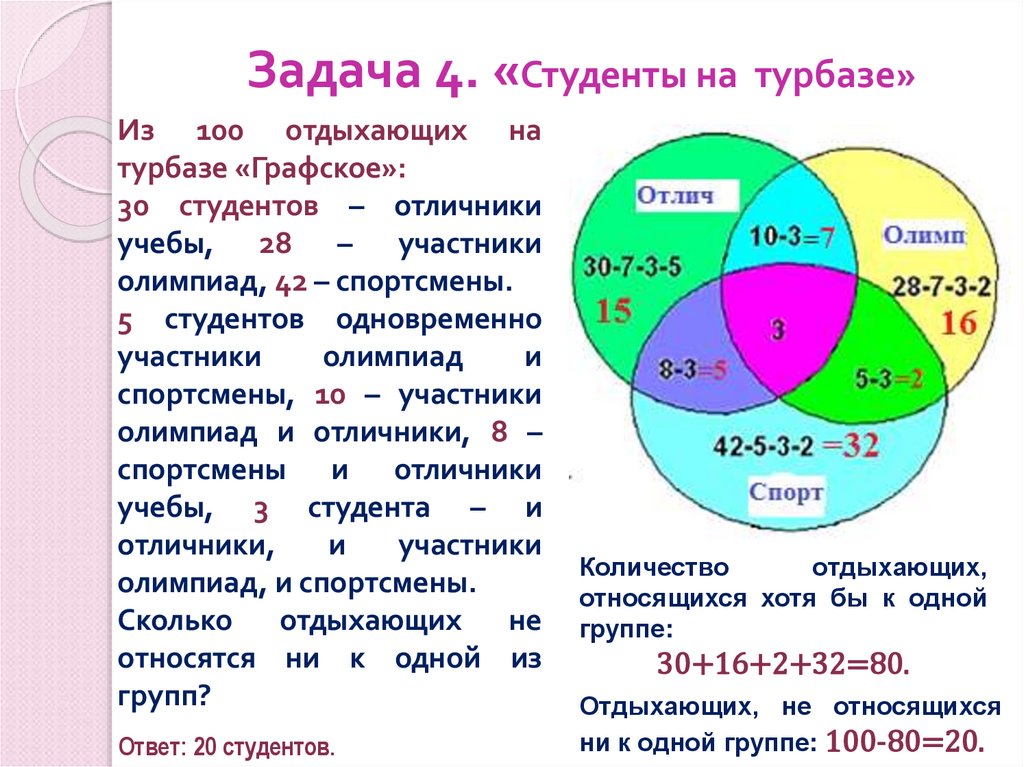
6. Задача 3.

Группа туристов из 100 человек пробыла в городе N три дня. За это
время в ресторане питались 28 туристов, фастфуде — 42, кофейне —
30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и
кофейне — 8; в фастфуде и кофейне — 5. Всего во всех трех местах
побывали три человека. Сколько туристов питалось в других местах и
не посетило ни одного из перечисленных?
Решение.
В условии задачи три множества — Р, Ф и К. Туристы, которые
пытались в ресторане, фастфуде и кофейне, соответственно.
Универсальное множество U — это множество всех туристов
группы. Запишем условие задачи, где n(X) — количество элементов
множества X.