Секущая окружности. Касательная к окружности

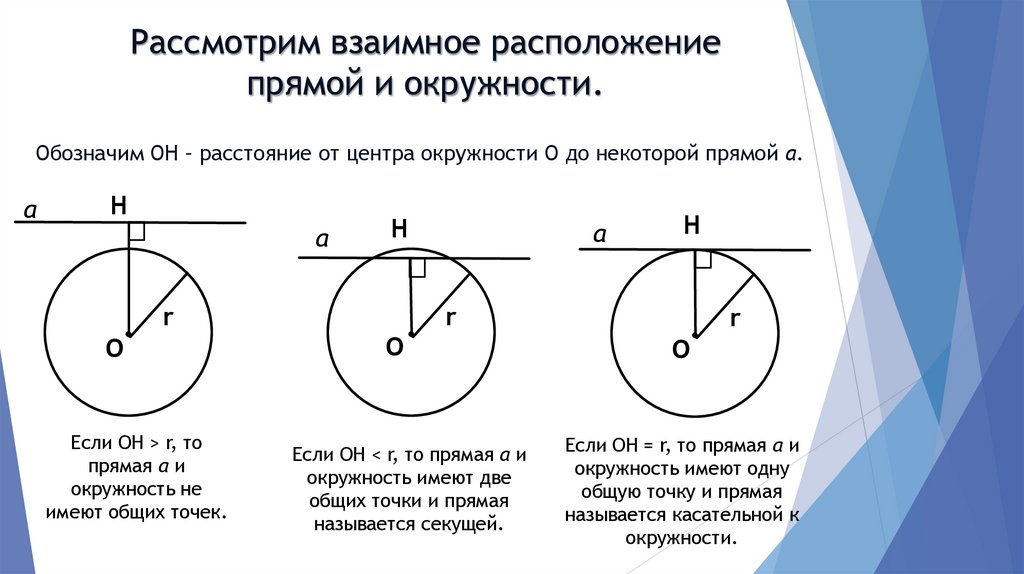
1. Рассмотрим взаимное расположение прямой и окружности.

Обозначим ОН – расстояние от центра окружности О до некоторой прямой а.
а
Н
а
Н
r
O
Если ОН > r, то
прямая а и
окружность не
имеют общих точек.
а
Н
r
O
Если ОН < r, то прямая а и
окружность имеют две
общих точки и прямая
называется секущей.
r
O
Если ОН = r, то прямая а и
окружность имеют одну
общую точку и прямая
называется касательной к
окружности.

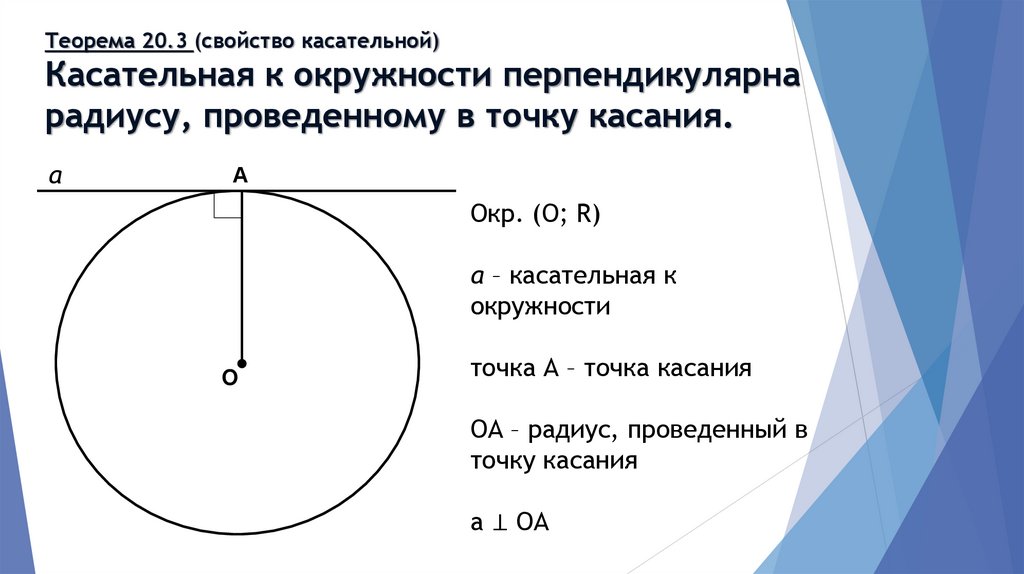
2. Теорема 20.3 (свойство касательной) Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

а
А
Окр. (О; R)
а – касательная к
окружности
O
точка А – точка касания
ОА – радиус, проведенный в
точку касания
а ⊥ ОА

3. Теорема 20.4 (признак касательной к окружности) Если прямая, проходящая через точку окружности, перпендикулярна радиусу,

проведенному в эту точку, то эта прямая
является касательной к данной окружности.
Следствие
Если расстояние от центра окружности до
некоторой прямой равно радиусу
окружности, то эта прямая является
касательной к данной окружности.