Similar presentations:
Методы искусственного интеллекта. Нечеткие множества и нечетная логика (лекция 4: часть 1 и часть 2)
1. МЕТОДЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА НЕЧЕТКИЕ МНОЖЕСТВА и НЕЧЕТНАЯ ЛОГИКА (Лекция 4: часть 1 и часть 2)
2.
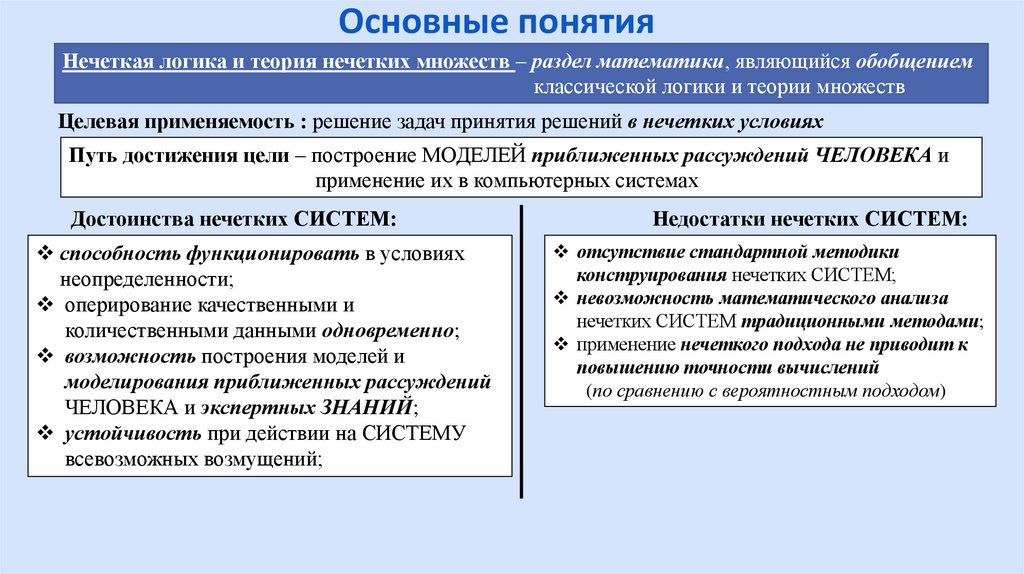
Основные понятияНечеткая логика и теория нечетких множеств – раздел математики, являющийся обобщением
классической логики и теории множеств
Целевая применяемость : решение задач принятия решений в нечетких условиях
Путь достижения цели – построение МОДЕЛЕЙ приближенных рассуждений ЧЕЛОВЕКА и
применение их в компьютерных системах
Достоинства нечетких СИСТЕМ:
способность функционировать в условиях
неопределенности;
оперирование качественными и
количественными данными одновременно;
возможность построения моделей и
моделирования приближенных рассуждений
ЧЕЛОВЕКА и экспертных ЗНАНИЙ;
устойчивость при действии на СИСТЕМУ
всевозможных возмущений;
Недостатки нечетких СИСТЕМ:
отсутствие стандартной методики
конструирования нечетких СИСТЕМ;
невозможность математического анализа
нечетких СИСТЕМ традиционными методами;
применение нечеткого подхода не приводит к
повышению точности вычислений
(по сравнению с вероятностным подходом)
3.
НЕЧЕТКИЕ МНОЖЕСТВА(Лекция 4: часть 1)
4.
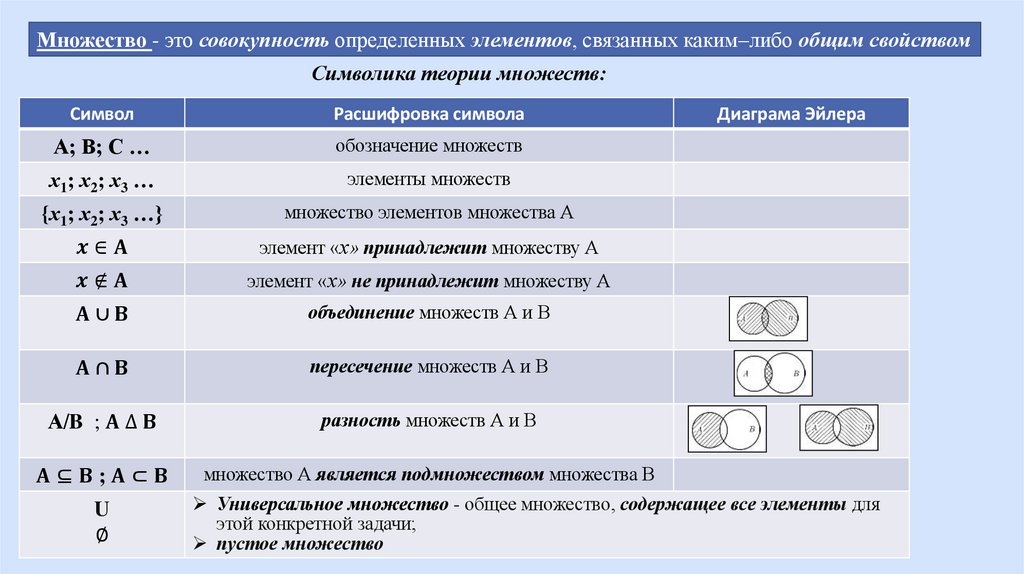
Множество - это совокупность определенных элементов, связанных каким–либо общим свойствомСимволика теории множеств:
Символ
Расшифровка символа
А; В; С …
обозначение множеств
х1; х2; х 3 …
элементы множеств
{х1; х2; х3 …}
множество элементов множества А





























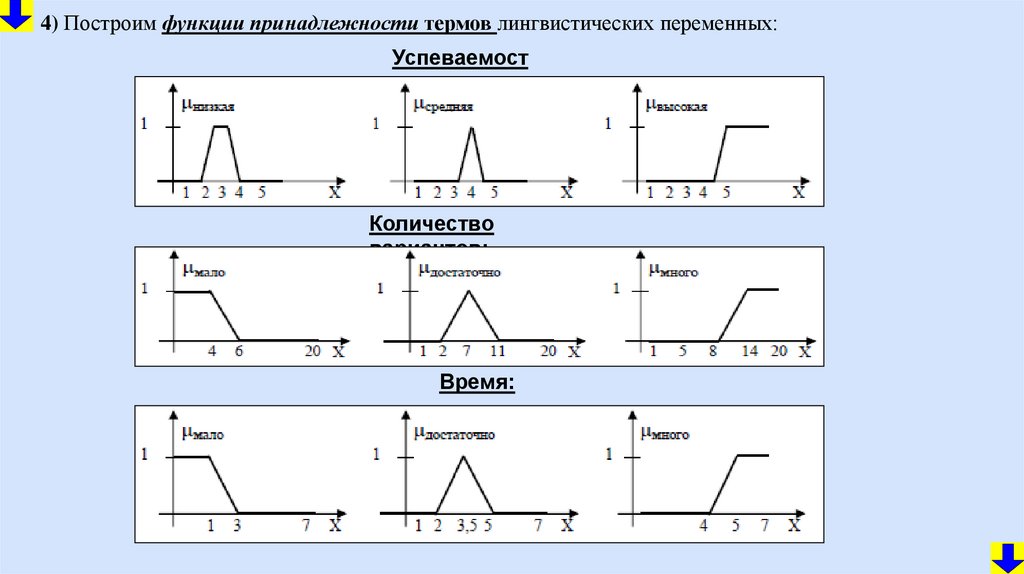



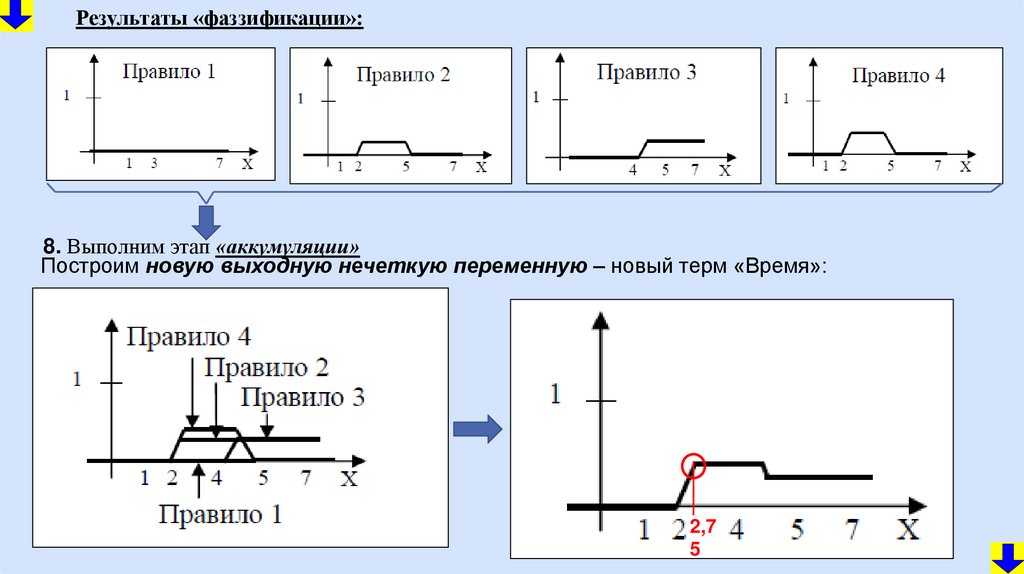

 mathematics
mathematics








