Моделирование управляемого демпфера

1.

1
МОДЕЛИРОВАНИЕ УПРАВЛЯЕМОГО ДЕМПФЕРА
А. Б. Корчагин
ФГБОУ ВПО «Омский государственный
технический университет»
Во второй половине 20 в. созданы устройства,
основанные на использовании жидкостей с
управляемой вязкостью : электрореологических
(ЭР) [5] и магнитореологических (МР) [6].

2. 2

Демпфирование в МР демпфере происходит в
процессе преодоления гидравлического
сопротивления движению МР жидкости в зазорах
между поршнем и стенками цилиндра или
клапана, причем вязкость МР жидкости
изменяется многократно под действием
магнитного поля, создаваемого обмотками
соленоидов, размещенных вокруг гидравлических
каналов [3].

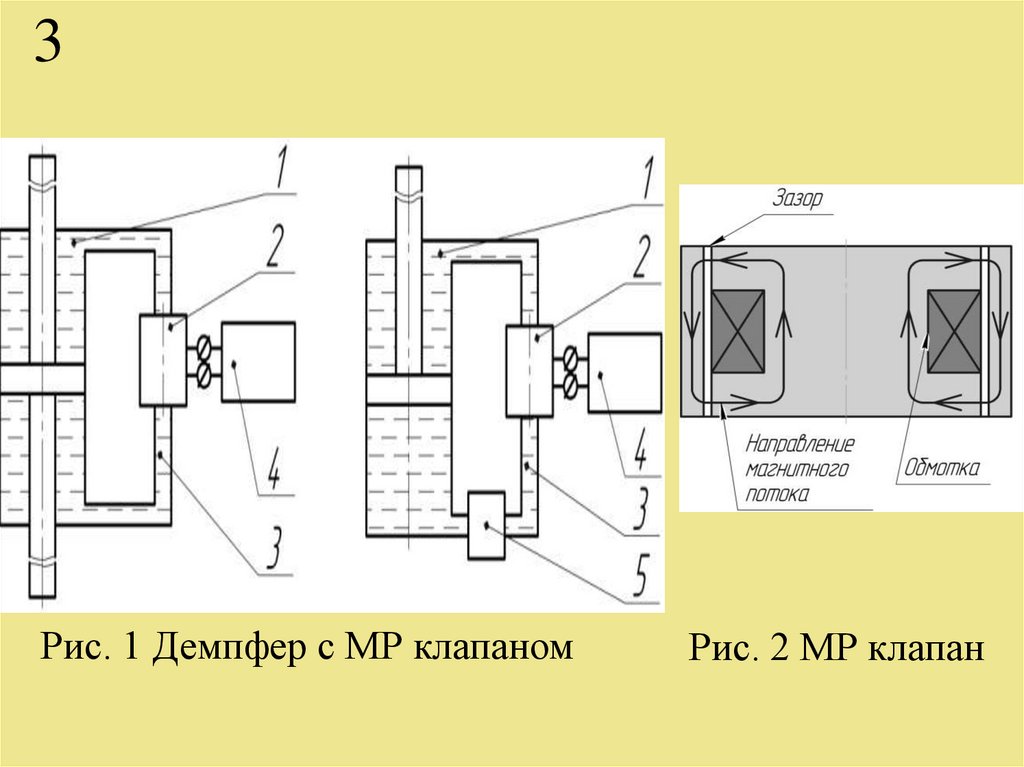
3. 3

Рис. 1 Демпфер с МР клапаном
Рис. 2 МР клапан

4. 4

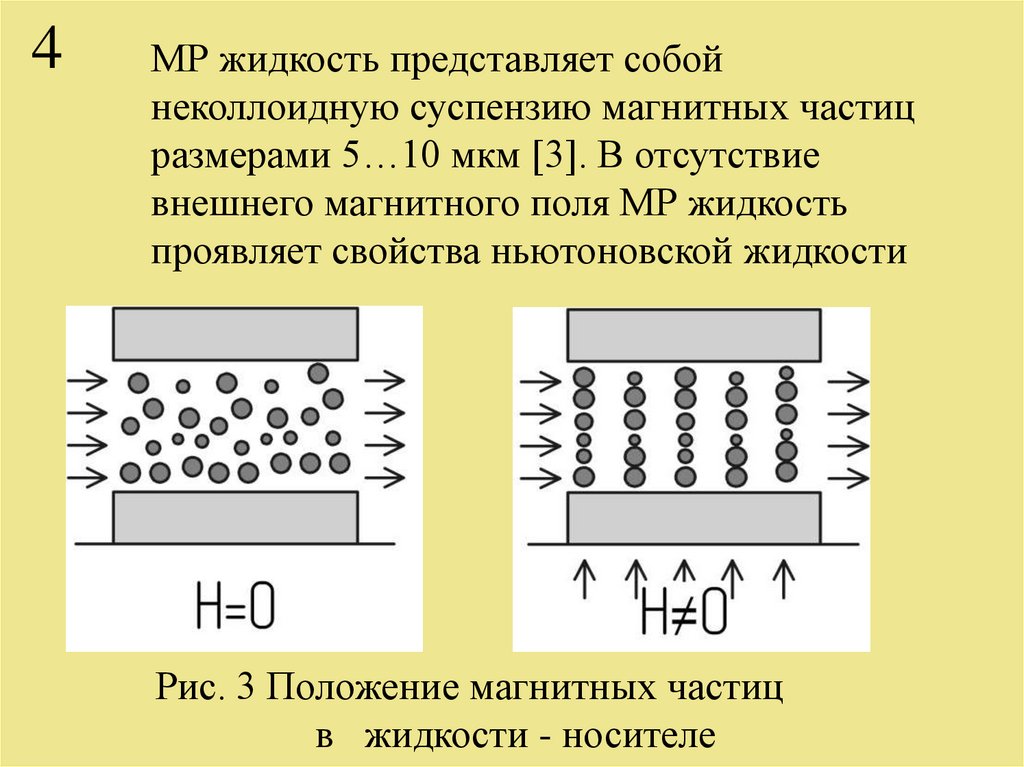
МР жидкость представляет собой
неколлоидную суспензию магнитных частиц
размерами 5…10 мкм [3]. В отсутствие
внешнего магнитного поля МР жидкость
проявляет свойства ньютоновской жидкости
Рис. 3 Положение магнитных частиц
в жидкости - носителе

5. 5

Вязкость МР жидкости обратимо изменяется
соответственно изменениям напряженности магнитного
поля, принимая состояния от жидкого до твердого,
проявляя при этом свойства неньютоновской жидкости.
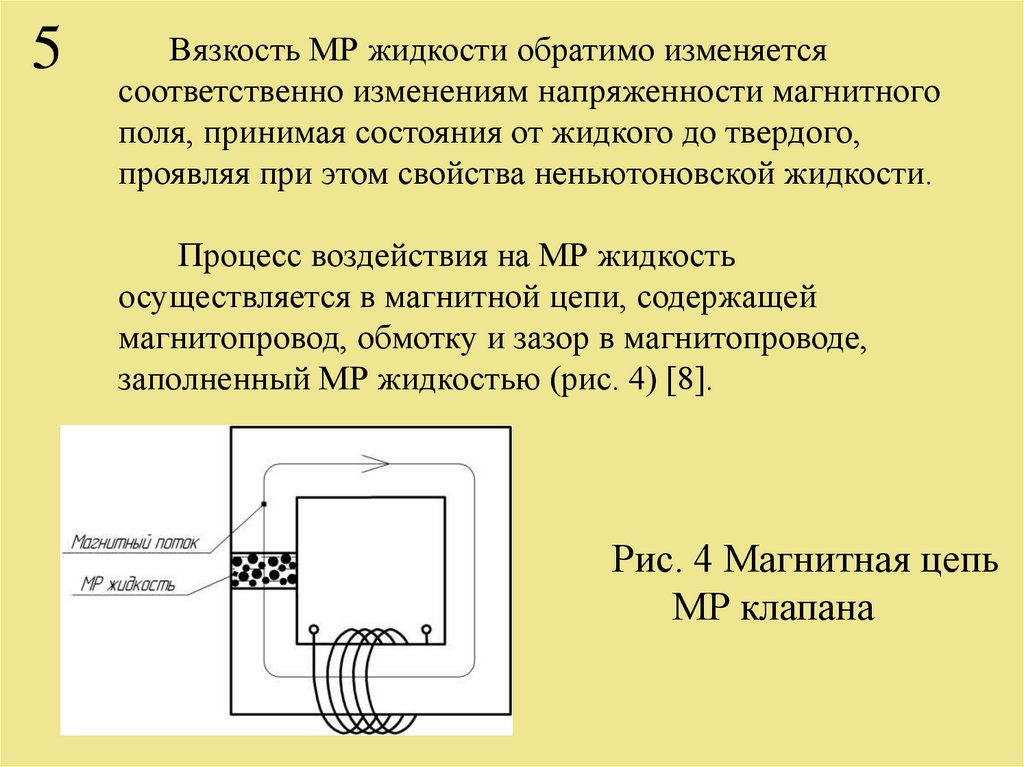
Процесс воздействия на МР жидкость
осуществляется в магнитной цепи, содержащей
магнитопровод, обмотку и зазор в магнитопроводе,
заполненный МР жидкостью (рис. 4) [8].
Рис. 4 Магнитная цепь
МР клапана

6. 6

Поведение МР жидкости описывается осесимметричной
моделью течения жидкости через кольцевой зазор МР
клапана, основанная на уравнениях Навье – Стокса для
течения Хагена – Пуазёйля [3].
При квазистатическом анализе осесимметричного
течения несжимаемой жидкости внутри клапана
инерцией жидкости пренебрегают вследствие ее
несущественности ( u x / x 0), поведение жидкости
описывается уравнением [3] :
x,r r
x,r r p
r
r
x
решение
C1
1 p x
x,r
r
2 x
r
(1)
(2)

7. 7

Решение (2) соответствует вязкопластической модели
Бингама :
u x r
u x r
x,r r y H , r sgn
r
r
(3)
где ρ и η – постоянные, r – радиальная координата, С1 –
постоянная, определяемая граничными условиями х –
продольная координата, p – градиент давления
x

8. 8

Рис. 5
Профиль
скорости
жидкости
в зазоре
МР
клапана
8
В областях І и ІІ сдвиговые напряжения превышают предел
текучести (3). Профиль скорости складывается из (2) и (3):
области І с граничными условиями: r = R1, ux (r) = v0,
r
1 dp 2
C
r
1
r R12 1 ln y r dr v0
ux r
4 dx
R1 R
(4)
1
для R1 ≤ r ≤ R2 ,
области ІI с граничными условиями: r = R1, ux (r) = v0,
R22
1 dp
C1 R
1
2
r ln y r dr
ux r
4 dx
r r
для r 2 ≤ r ≤ R2 ,
2
2
(5)

9. 9

,
9
области С (области «поршневого» течения), где напряжение
сдвига меньше предела текучести, поэтому сдвигового
течения нет.
y (r1 ) = y (r 2) = y (H)
r1r2
Из (2) и (6) следует Ñ 1
y H
r2 r1
(6)
(7)
2 y H
Из (1) следует
r2 r1 dp
(8)
dx
Перепад давления определяется в МР клапане с учетом его
конструктивных параметров (рис. 6) :
dp
1
r1r2
R2 r1
hRm r2 r1 r2 r1 2 y
ln
2 y 2 Rm r1 r2 2 v0 0
dx
2
r2 r1 R1r2
(9)

10.

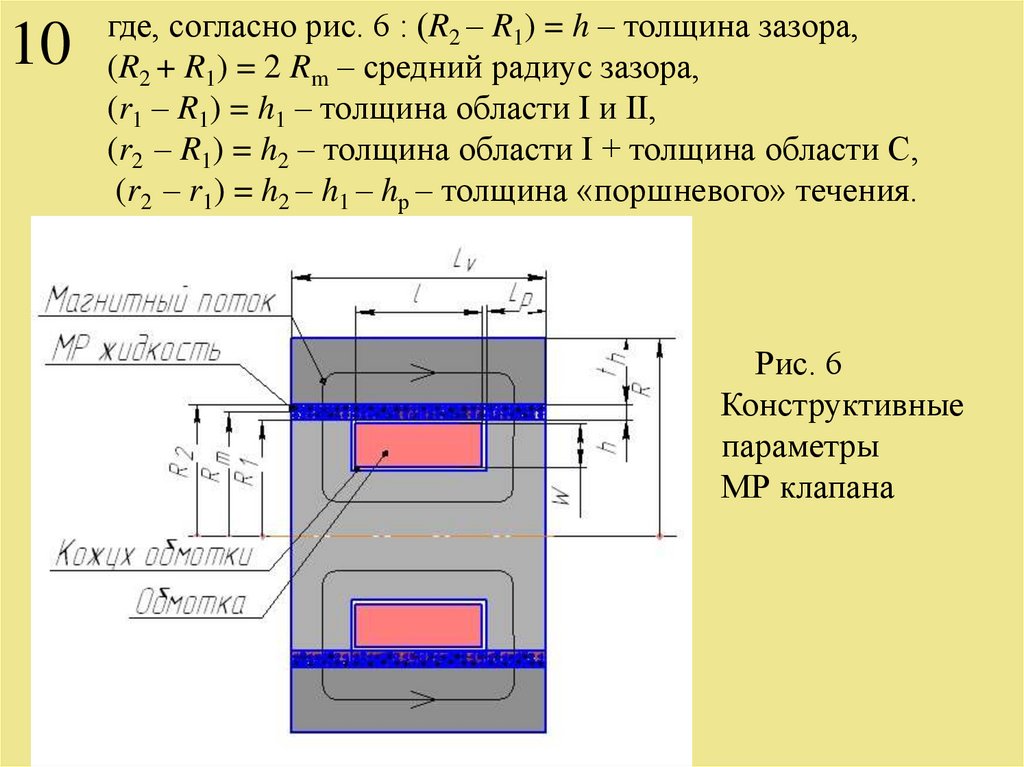
10
где, согласно рис. 6 : (R2 – R1) = h – толщина зазора,
(R2 + R1) = 2 Rm – средний радиус зазора,
(r1 – R1) = h1 – толщина области І и ІІ,
(r2 – R1) = h2 – толщина области І + толщина области С,
(r2 – r1) = h2 – h1 – hр – толщина «поршневого» течения.
Рис. 6
Конструктивные
параметры
МР клапана

11.

11
,
,
.
Определение расхода :
dp
2
Q R1 v0 2hRm h 2 2 R1R2 r24 r14
8 dx
(10)
8 y
4r1r2
2
2
2 gRm r2 r1
2 Rm h 2 R1 R2 r23 r13
r2 r1
3
Перепад давлений, достигаемый на выходе из
кольцевого зазора по сравнению с давлением на
входе :
dp
p
L
(11)
где L – общая длина магнитного полюса. Окончательно, на
основании модели Бингама, получается следующее [8] :
dx
Lp
6 L
PA PA,η PA,τ 3 Q 2c y
h Rm
h
(12)
где Q v p Ap Rm h , Lp – длина магнитного полюса, L = 2Lp.

12.

12
,
В уравнении (12) параметр с – функция профиля скорости
течения, выражаемая в виде [3] :
12 Ap v p
1
. (13)
c 2.07
2.07
1 0.4 N 3
12 Ap v p 0.4 Ag h y
где N3 – безразмерная переменная
Rm h 2 y
N3
6 Ap v p
(14)
tp – ширина полюса, L – длина магнитного полюса.
Согласно [3, 8], значения параметра с изменяются в пределах от
2 (при ∆р / ∆рη менее 1) до 3 (при ∆р / ∆рη более 100).
Учитывая, что площадь зазора равна 2πRmh = Аg , из (12)
следует :
где. AR R Ap
m
2
m
Ag
2
p
12 AR v p
m
Ag h 2
(15)

13.

и
13
Развиваемая МР клапаном с кольцевым зазором
демпфирующая сила определяется в виде :
Fd pAp p Ap p Ap F F
(16)
или, с учетом (9)
F
12 AR v p
m
Ag h
2
LAp и F
c y H Ap
h
L
(17)
Диапазон управления МР клапана определяется в виде
p
p
с учетом Wm = Q∆р (где Wm – управляемая механическая энергия) и
Таким образом, приведены основные расчетные
параметры для определения технических характеристик
МР клапана.

14.

14
Выполнено моделирование в комплексе ANSYS
процессов, происходящих в МР жидкости под
воздействием магнитного поля [9].
Рис. 8 Фрагменты модели МР клапана

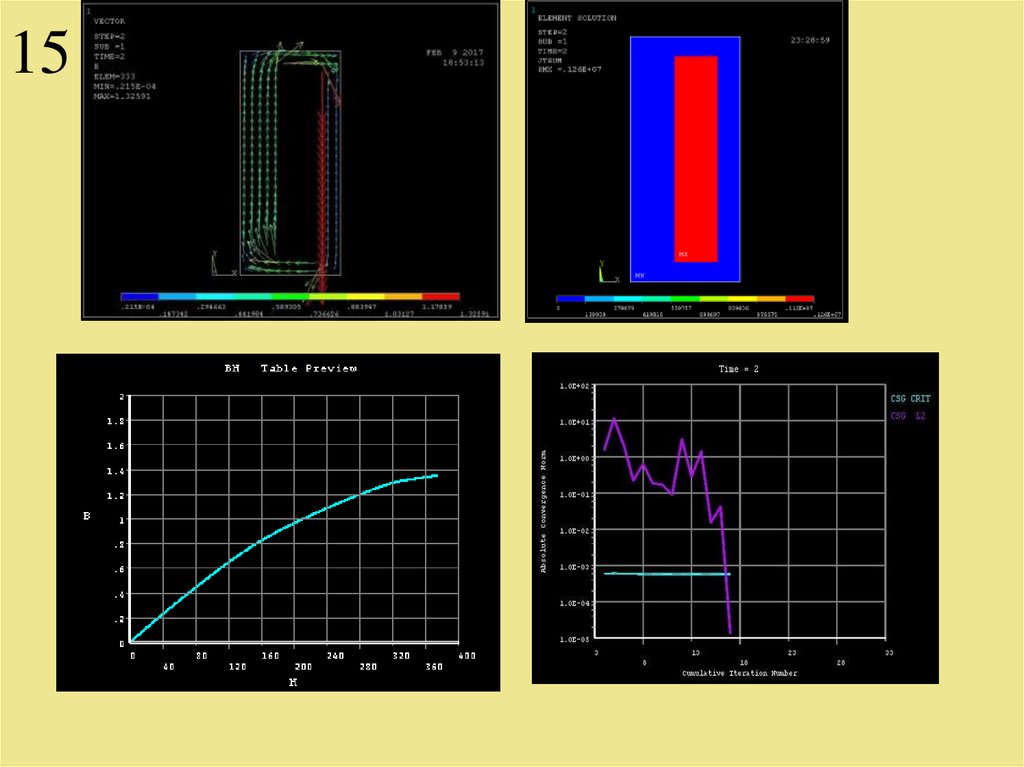
15.

15

16. Моделирование МР клапана выполняется в комплексе ANSYS с целью оптимизации конструктивных параметров устройства

16
Моделирование МР клапана выполняется в
комплексе ANSYS с целью оптимизации
конструктивных параметров устройства
Рис. 6 МР клапан
Рис. 7 Детали
МР клапана

17.

17
Библиографический список
1.Колмаков В. И. Динамика сухопутных систем специального назначения: монография.
– Волгоград, 2009. – 324 с.
2.Дербаремдикер А. Д. Гидравлические амортизаторы автомобилей. – М.:
Машиностроение. 1969. – 236с.
3.Guglielmino, E. Semi-active Suspension Control / E. Guglielmino, T. Sireteanu, C. W.
Stammers et al. – Springer, Verlag London Limited // 2008.– 294 p. – ISBN 978-1-84800230-2.
4.Savaresi, S.M. Semi-Active Suspension Control Design for Vehicles / S.M. Savaresi, C.
Poussot-Vassal et al. – Elsevier, 2010. – 240 p. – ISBN: 978-0-08-096678.
5.US patent 2,417,850 Method and means for translating electrical impulses into mechanical
forces / W. M. Winslow. – Filed Sept. 27, 1947. Jan. 26, 1954.
6.US Patent 2,667,237 Magnetic Fluid Shock Absober / J. Rabinow. – Filed Sept. 27, 1948.
Jan. 26, 1954.
7.Gorodkin S. Magnetorheological Throttle Valve in Passive Damping System / S. Gorodkin,
A. Lucianovich, W. Kordonsky // Journal of Intelligent Material System and Structures, Vol. 9
– August 1998/ pp. 637 – 641.
8.Quoc-Hung Nguyen Optimal Design Methodology of Magnetorheological Fluid Based
Mechanisms / Quoc-Hung Nguyen and Seung-Bok Choi: Smart Actuation and Sensing
Systems – Recent Advances and Future Challenges / Edited by Giovanni Berselli, Rocco
Vertechy and Gabriele Vassura, ISBN 978-953-51-0798-9, 728 pages, Publisher: InTech,
Chapters published October 17, 2012 under CC BY 3.0 license, DOI: 10.5772/2760, рр 347 –
382. Режим доступа: http://dx.doi.org/10.5772/51078 .

18.

18
9. Huei-Huang Lee Finite Element Simulations with ANSYS Workbench 14. Theory,
Applications, Case Studies: SDC publications, 2012. – 608 p. Сайт
автора: http://myweb.ncku.edu.tw/~hhlee/Myweb_at_NCKU/ANSYS14.html .
10. Mosher M. and Tanner E.T. A Numerical Investigation of Combined Shock
and Vibration Isolation Through the Semi-active Control of a Magnetorheological
Fluid Damper in Parallel with an Air Spring. – Proceeding of the 71 st
SAVIAC Shock Vibration Symposium, Arlington, Virginia, November 6 - 9, 2000.
– 14 с.
11. Koch G. Experimental validation of a new adaptive control approach for a hybrid
suspension system / G. Koch, S. Spirk, E. Pellegrini, N. Pletschen and B.
Lohmann. In Proceding of the 2011 American Control Conference on O'Farrell
Street, San Francisco, CA, USA, June 29 – July 01, 2011. – рр. 4580 – 4586.
12. Litak G. Chaotic vibration of a quarter-car model excited by the road surface
profile / G. Litak, M. Borowiec, M. I. Friswell, K. Szabelski. – Communications
in Nonlinear Science and Numerical Simulation. 13 (2008). рр. 1373 – 1383.
13. Verros G. Design Optimization of Quarter - car Models with Passive and Semiactive Suspensions under Random Road Excitation / G. Verros, S. Natslavas, C.
Papadimitriou // Journal of Vibration and Control. 11, 2005. – pp. 581– 606.
Спасибо за внимание

19. И еще