Прямолинейное равномерное движение

1. Прямолинейное равномерное движение

2.

3.

Математика — «язык» физики.
1) Функция — это зависимость одной переменной величины от другой.
Например, в математике — y=y(x), в кинематике движение материальной точки на плоскости описывается двумя
координатами x и y, которые зависят от времени: x=x(t) (рис. 2), y=y(t).
2) При равномерном прямолинейном движении материальной точки (модель реального движения) её координата является линейной
функцией времени:
x=x0+υx(t−t0)(1).
Обозначения: x0 — начальная координата в начальный момент времени t0, x — координата в произвольный момент
времени t, vx — проекция вектора скорости на ось OX.
3) Формула (1) определяет координату исследуемой точки, но не пройденный путь (длину отрезка траектории, пройденного телом за
время Δt=t−t0).
4) Уравнение траектории движущегося тела — функциональная зависимость, связывающая координаты x и y (при описании
движения на плоскости).

4.

Векторные и скалярные
величины в физике

5.

Векторное и скалярное уравнения
движения материальной точки

6.

Средняя путевая скорость
Физическое понятие «скорость» является неоднозначным термином: зависимость от
расстояния и времени позволяет ввести два понятия скорости, так как в физике
используются векторные (перемещение) и скалярные (модуль
перемещения, пройденный путь, время) величины.

7.

Средняя путевая скорость
Физическое понятие «скорость» является неоднозначным термином: зависимость от
расстояния и времени позволяет ввести два понятия скорости, так как в физике
используются векторные (перемещение) и скалярные (модуль
перемещения, пройденный путь, время) величины.

8.

Средняя путевая скорость

9.

Аналитический и графический способы
решения задач
Физическую задачу в кинематике можно решить несколькими способами:
•аналитический — решение задачи основано на формулах (физических законах), которые
связывают искомую величину и данные в условии задачи;
•графический — решение задачи осуществляется с помощью графика.

10.

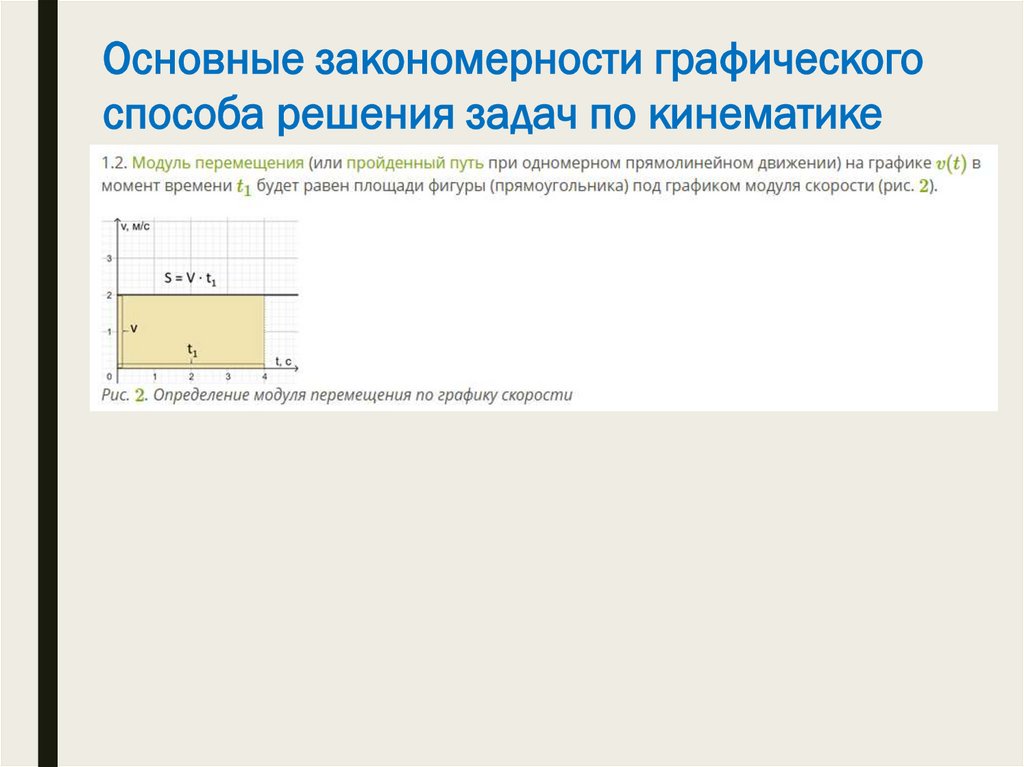
Основные закономерности графического
способа решения задач по кинематике

11.

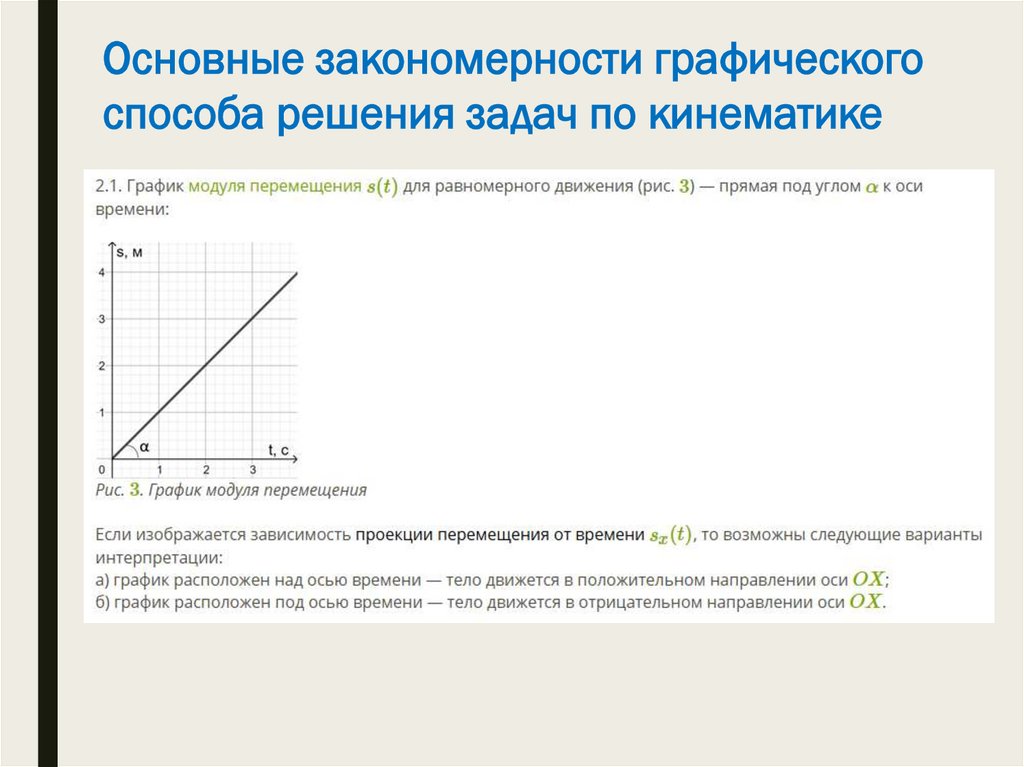
Основные закономерности графического
способа решения задач по кинематике

12.

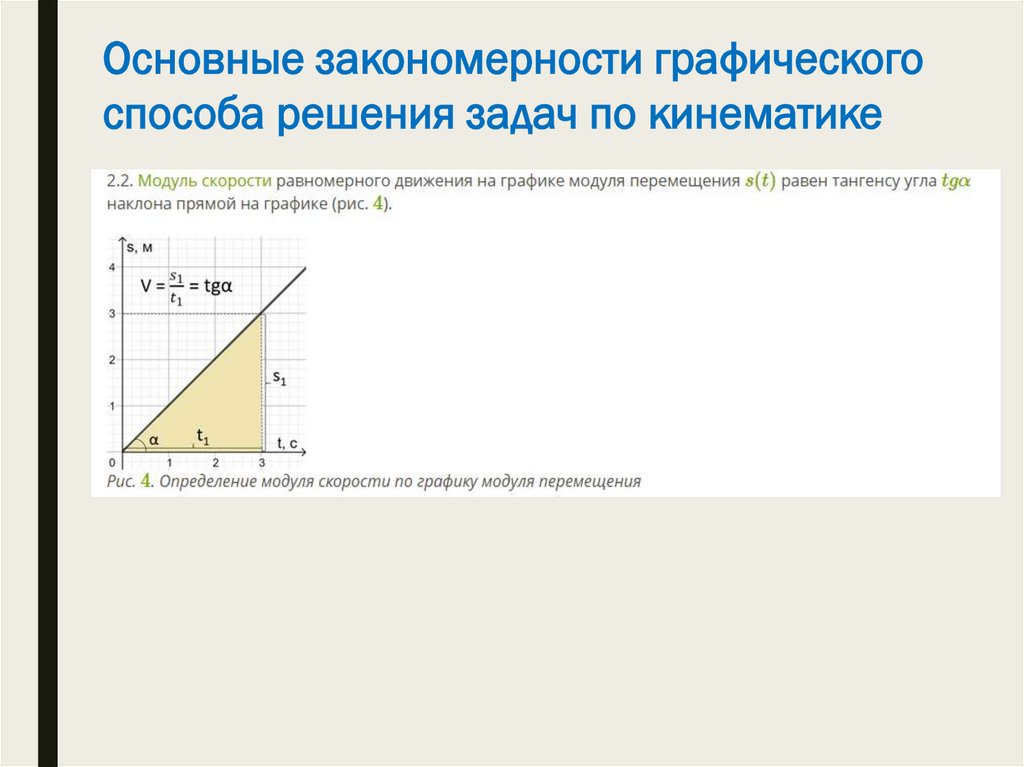
Основные закономерности графического
способа решения задач по кинематике

13.

Основные закономерности графического
способа решения задач по кинематике

14.

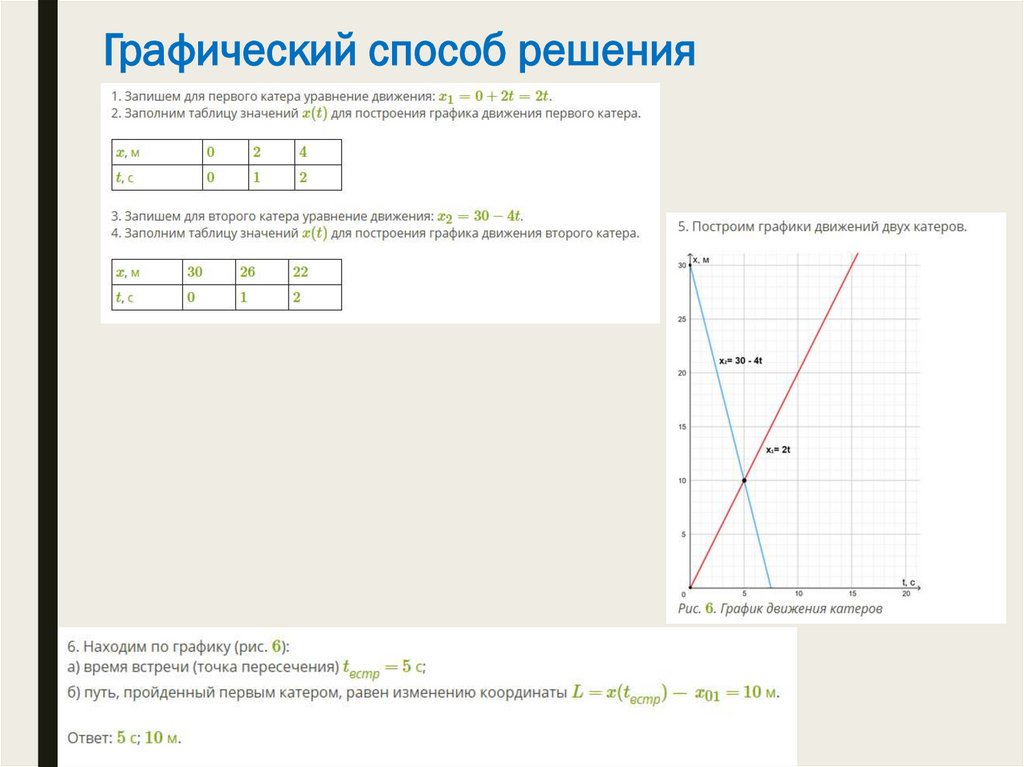
Решение задачи аналитическим и
графическим способами

15.

Аналитический способ решения

16.

Графический способ решения