Реальные газы

1. РЕАЛЬНЫЕ ГАЗЫ

I Межмолекулярное
взаимодействие.
II Уравнение Ван–дер-Ваальса.
III Изотермы Ван-дер-Ваальса.

2. I Межмолекулярное взаимодействие.

• Разряженные реальные газы при не слишком
низких температурах с достаточной степенью
точности подчиняются законам идеальных
газов. Повышение давления приводит к
уменьшению среднего расстояния между
молекулами, поэтому необходимо учитывать
объем молекул и взаимодействие между ними.
• Реальные газы – газы, свойства которых
зависят от взаимодействия молекул. При их
рассмотрении необходимо учитывать силы
межмолекулярного взаимодействия.

3.

• Атомы и молекулы вещества – сложные
системы движущихся заряженных
частиц, между которыми действуют
силы притяжения и отталкивания
электрического происхождения. Эти
силы короткодействующие. Они
становятся пренебрежимо малыми уже
на расстояниях порядка трех – четырех
диаметров молекулы, причем силы
отталкивания убывают с расстоянием
быстрее, чем силы притяжения.

4.

• Рассмотрим две молекулы 1 и 2.
Проведем через центры молекул ось r в
направлении от 1 молекулы ко 2 (рис.а).
Fпр<0, Fот>0. График зависимости сил
от расстояний между молекулами рас.б.

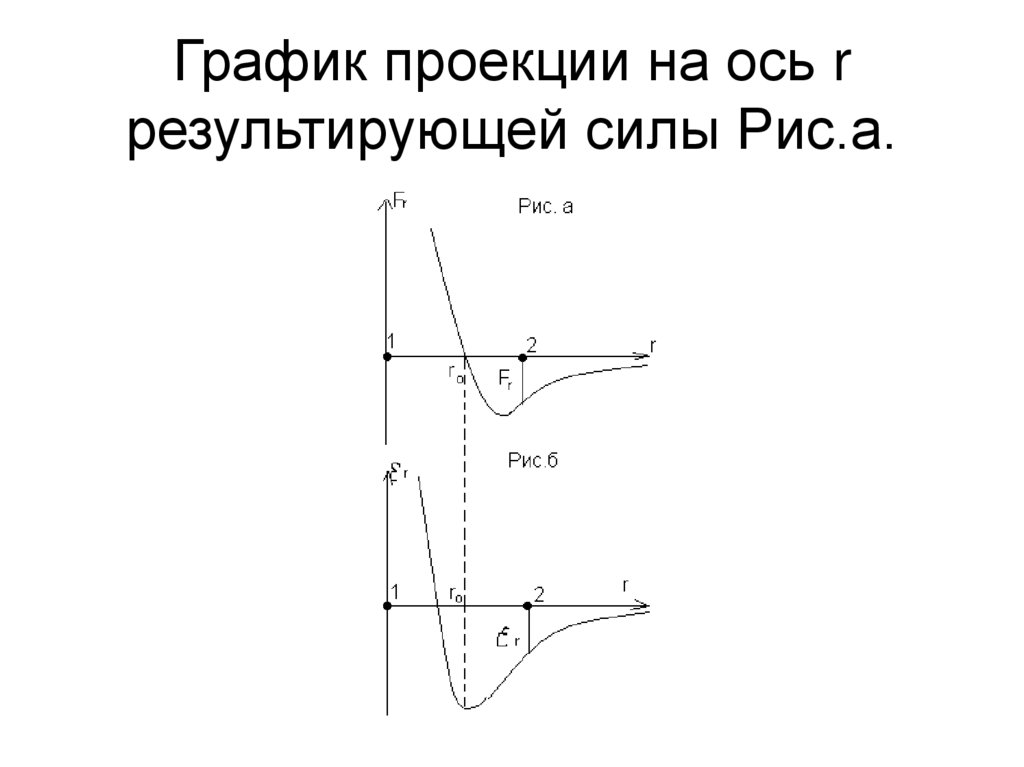
5. График проекции на ось r результирующей силы Рис.а.

6.

• Из графика видно: 1) если r<ro –
преобладают силы отталкивания, 2)
если r>ro – преобладают силы
притяжения, 3) если r=ro – равны.
• Силы межмолекулярного
взаимодействия – консервативные
силы. Эти силы обуславливают наличие
взаимной потенциальной энергии
Рис.б. Расстоянию ro соответствует
минимум потенциальной энергии
(потенциальная яма) и равновесное
положение молекул.

7.

• На расстоянии ro располагались бы
молекулы в отсутствие теплового
движения (Т=0). Глубина потенциальной
ямы
определяет абсолютную
величину той работы, которую
необходимо совершить против сил
притяжения, чтобы молекулы из
положения равновесия смогли удалиться
на сколь угодно большие расстояния друг
от друга. Эту работу молекулы могут
совершить за счет кинетической энергии
теплового движения. При Т 0
молекулы одновременно обладают и
потенциальной и кинетической энергией.
п min

8.

• Агрегатное состояние и
характер теплового
движения атомов и молекул
вещества зависит от
соотношения между средней
кинетической энергией
теплового движения
и абсолютной величиной
.
k
п min

9.

• 1) Если k << п min , т.е. полная энергия
велика и отрицательна. Вещество находится в
твердом кристаллическом состоянии. Запаса
кинетической энергии молекул недостаточно
для того, чтобы совершить работу против сил
притяжения и удалиться на большое
расстояние. Тепловое движение молекул
проявляется в малых колебаниях около
положения равновесия. Совокупность
равновесных положений молекул образует
кристаллическую решетку.
• 2) Если k >> п min , т.е. полная энергия
молекул положительна, то вещество находится
в газообразном состоянии.

10.

• Средняя кинетическая энергия теплового
движения велика и ее вполне достаточно
для того, чтобы разорвать связи между
молекулами, перевести их в почти
свободное состояние. Удаляясь друг от
друга, молекулы легко преодолевают силы
притяжения, поэтому газ занимает весь
предоставленный ему объем.
• 3) Если k ≈ п min
, то вещество
находится в жидком состоянии, так как в
результате теплового движения молекулы
перемещаются в пространстве,
обмениваясь местами, но не расходясь на
расстояние, превышающее ro.

11. II Уравнение Ван–дер-Ваальса.

• Чтобы получить уравнение
состояния реального газа,
необходимо внести в уравнение
состояния идеального газа
поправки, учитывающие силы
межмолекулярного
взаимодействия.

12.

• 1) Поправка на собственный объем
молекул (учет сил отталкивания). Так как
молекулы реальных газов нельзя считать
материальными точками, они сами
занимают некоторый объем и этот объем
недоступен для их движения. Учтем этот
недоступный объем в виде поправки b (b объем, занимаемый самими молекулами),
тогда уравнение состояния для 1 моля
примет вид p(Vm -b)=RT. Для подсчета
недоступного объема предположим, что
имеют место только парные столкновения
молекул. Сталкиваясь, две молекулы
сближаются на расстояние d, равное
эффективному диаметру.

13.

• Для центров обеих молекул недоступным
является объем сферы радиуса d.
4 3
,
Vсф d
3
• а объем молекулы
4 d
V
,
3 2
• тогда
V
8
V
,
• т.е. для двух молекул недоступным будет
объем превышающий объем одной
молекулы в 8 раз. В расчете на одну
молекулу, недоступным оказывается
объем, равный учетверенному объему
одной молекулы.
3
M
сф
M

14.

• 2) Поправка на внутреннее давление (учет
сил притяжения). Действие сил притяжения
газа приводит к появлению
дополнительного давления на газ,
называемого внутренним давлением. По
вычислениям Ван-дер-Ваальса, внутреннее
давление обратно пропорционально
квадрату молярного объема
a
p 2
(1), где а –
Vm
постоянная Ван-дер-Ваальса,
характеризующая силы межмолекулярного
притяжения, Vm – молярный объем.

15.

Реальные газы. Уравнение Ван-дер-Ваальса
m
pV
RT
M
Необходимость введения поправок в
уравнение Менделеева-Клапейрона
1. Наличие объема молекул
2. Наличие притяжения молекул
a
( p 2 )(V b) RT Для 1 моля газа:
V
Уравнение
Ван-дер-Ваальса
Ян Ван-дер-Ваальс
Johannes van der Waals
(1837—1923)
— голландский физик,
лауреат Нобелевской премии
по физике в 1910 г.

16.

a
( p 2 )(V b) RT
V
b – поправка,
учитывающая наличие
собственного объема
молекул.
a – поправка, учитывающая наличие притяжения
молекул, ослабляющего давление газа.
Уравнение Ван-дер-Ваальса
для
произвольного количества вещества
a
p 2
V
2
V
b RT

17.

• Т.к. V=νVm=>Vm=V/ν, тогда
2a V
2a
p 2 b RT или p 2 V b RT
V
V
• (3), где а и b – постоянные для каждого
газа величины, определяемые опытным
путем. Уравнение Ван-дер-Ваальса
более точно, чем уравнение
Менделеева – Клапейрона, но и оно
приближенное.

18. III Изотермы Ван-дер-Ваальса.

• Из уравнения (2):
a
p 2 Vm b RT / V 2 p
Vm
, получим
RT pb 2 a
ab
V V
V
0 (4) –
p
p
p
3
• уравнение третьей степени относительно
V.

19.

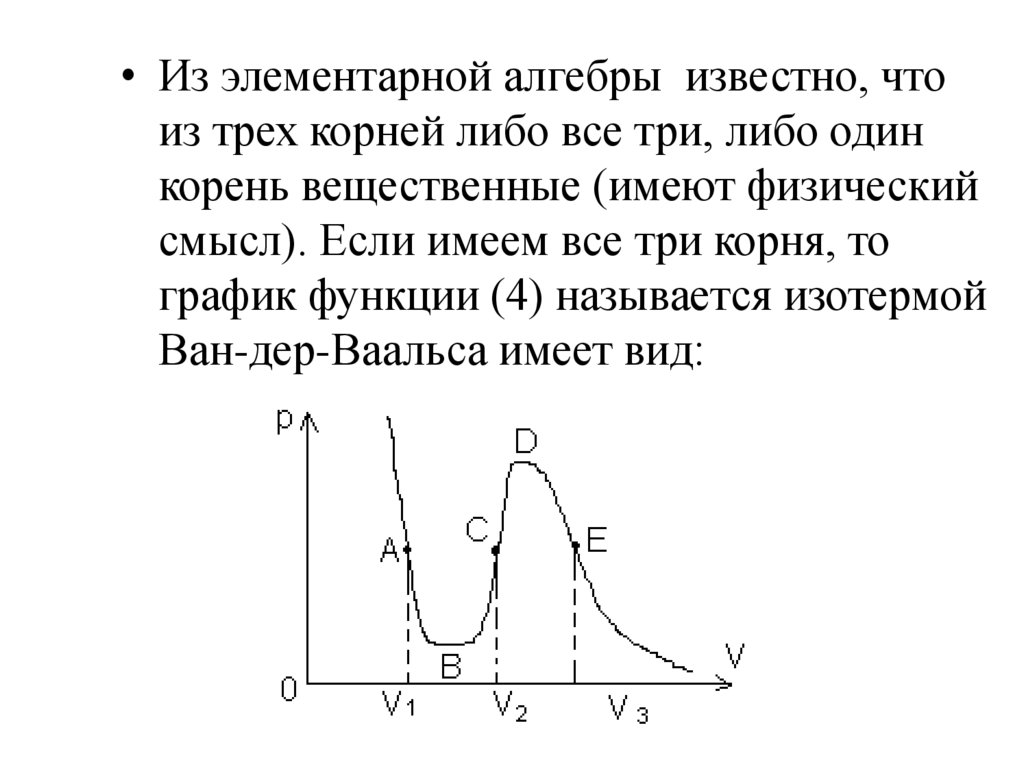
• Из элементарной алгебры известно, что
из трех корней либо все три, либо один
корень вещественные (имеют физический
смысл). Если имеем все три корня, то
график функции (4) называется изотермой
Ван-дер-Ваальса имеет вид:

20.

a
p 2
V
2
V
b RT
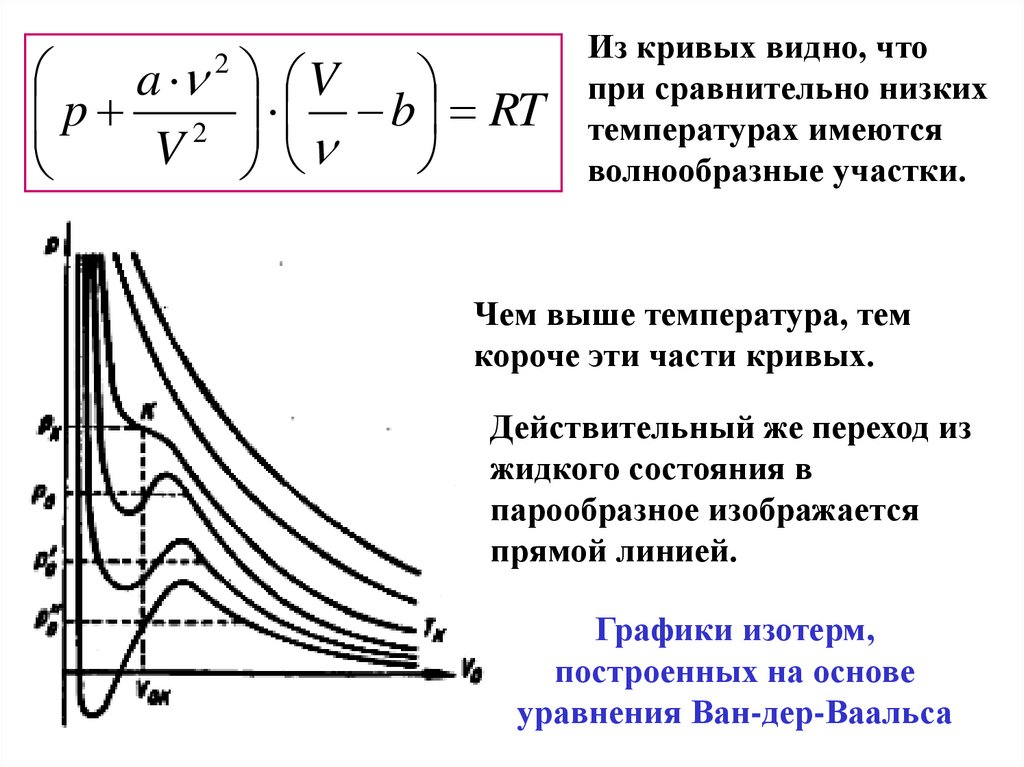
Из кривых видно, что
при сравнительно низких
температурах имеются
волнообразные участки.
Чем выше температура, тем
короче эти части кривых.
Действительный же переход из
жидкого состояния в
парообразное изображается
прямой линией.
Графики изотерм,
построенных на основе
уравнения Ван-дер-Ваальса

21.

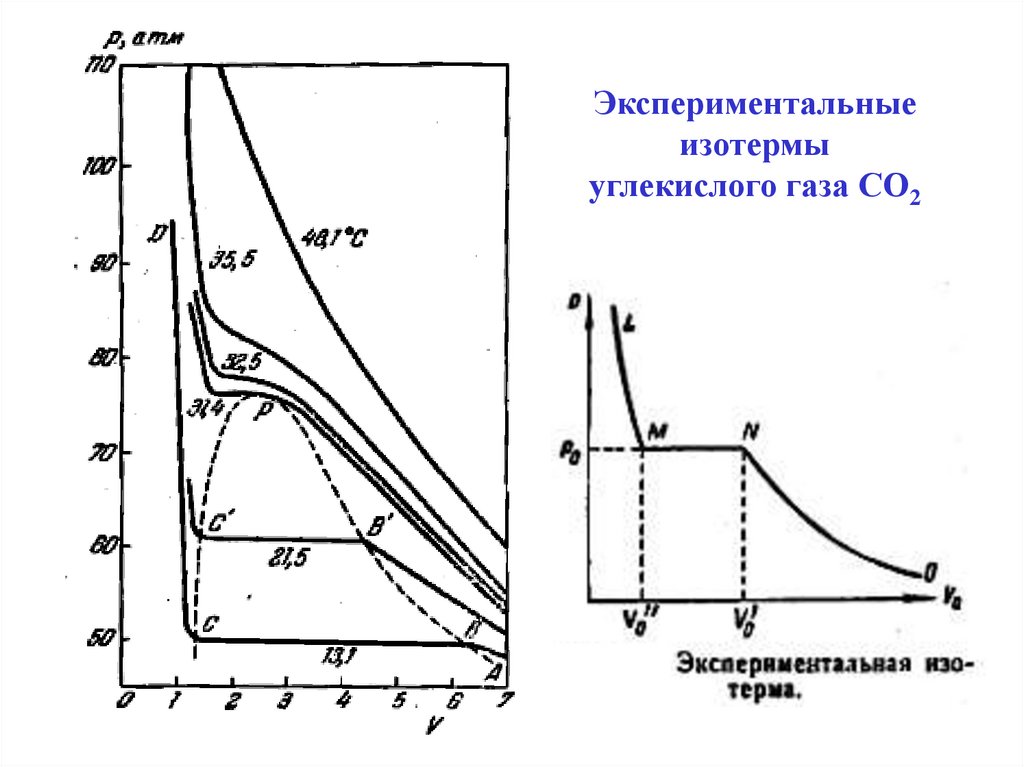
Экспериментальные
изотермы
углекислого газа СО2

22.

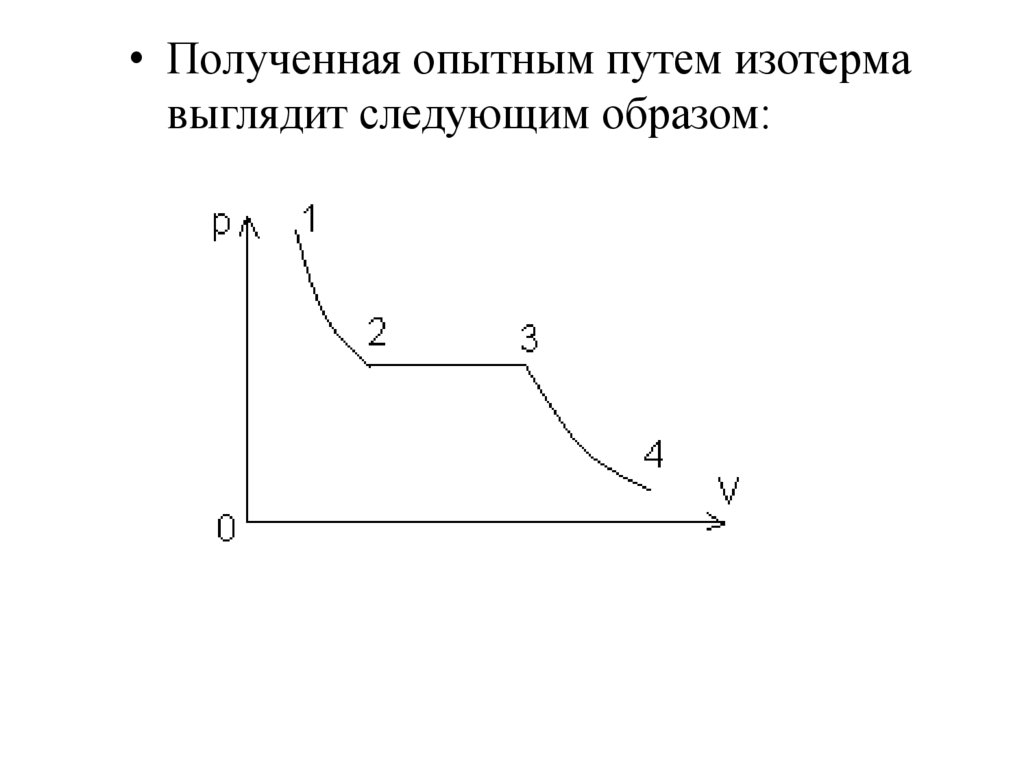
• Полученная опытным путем изотерма
выглядит следующим образом:

23.

• Часть 4 – 3 отвечает газообразному
состоянию, а часть 2 – 1 – жидкому. В
состояниях, соответствующих
горизонтальному участку изотермы 3 –
4, наблюдается равновесие жидкой и
газообразной фаз вещества. Переход из
газообразного состояния в жидкое
теоретически должен происходить по
изотерме EDCBA, но практически идет
по изобаре 3 – 2, которая является
реальной изотермой. При этом площадь
фигур АВС и СDE равны.

24.

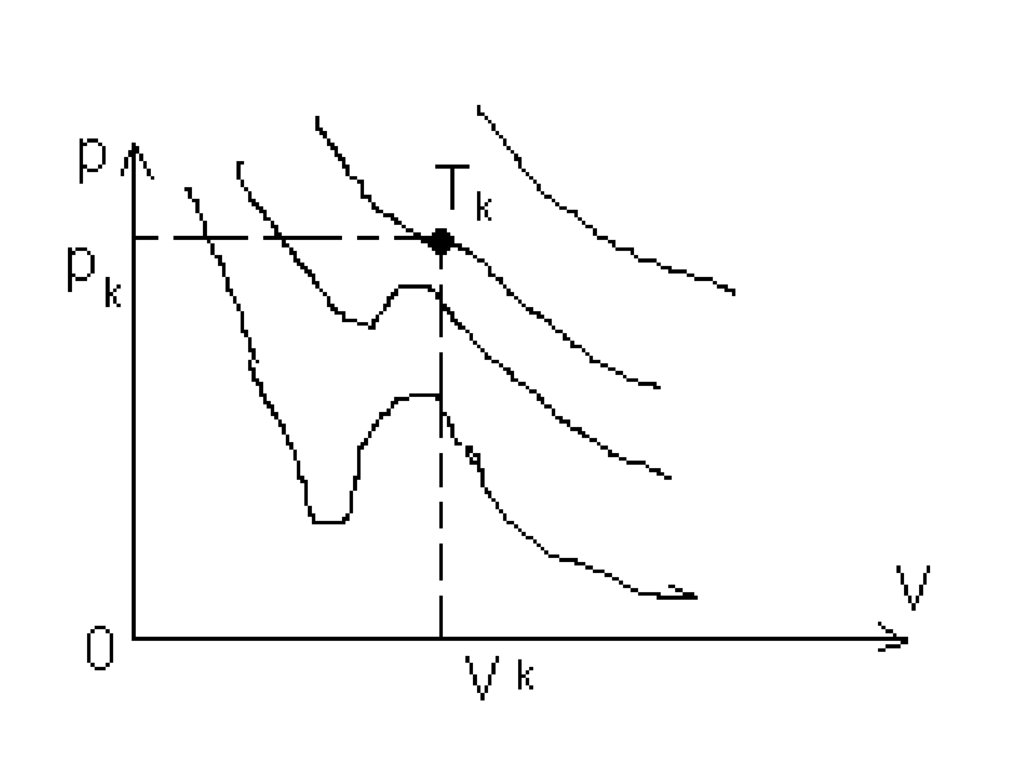
• С ростом температуры область горбов и
впадин на изотерме Ван-дер-Ваальса
уменьшается. При некоторой
температуре, называемой критической
Тк, на изотерме имеется лишь одна
точка перегиба, которая называется
критической точкой.
Соответствующие этой точке объем Vк
и давление рк называются также
критическими. При температуре выше
критической изотермы имеют вид
гиперболы.

25.

26.

• Связь критических параметров с
поправками Ван-дер-Ваальса:
p k V ab, 3 p k V a, 3 p k Vk RTk p k b
3
k
2
k
• Решая полученные уравнения, найдем:
a
8a
Vk 3b, p k
,
T
k
2
27 Rb
27b

27.

• Вещество в газообразном состоянии при
температуре ниже критической
называется паром, а пар, находящийся в
равновесии со своей жидкостью,
называется насыщенным.
• Критическое состояние вещества –
состояние, при котором исчезает всякое
различие между жидкостью и ее
насыщенным паром. Оно характеризуется
следующими особенностями:

28.

• 1) плотности жидкости и ее насыщенного пара
одинаковы;
• 2) исчезают силы поверхностного натяжения;
• 3) теплота парообразования равна 0;
• 4) давление насыщенного пара данного вещества
не может быть больше критического давления
этого вещества;
• 5) объем вещества в жидком состоянии не может
быть больше его критического объема;
• 6) при температурах выше критической вещество
может существовать только в газообразном
состоянии и никаким изотермическим сжатием
его невозможно перевести в жидкое состояние.

29.

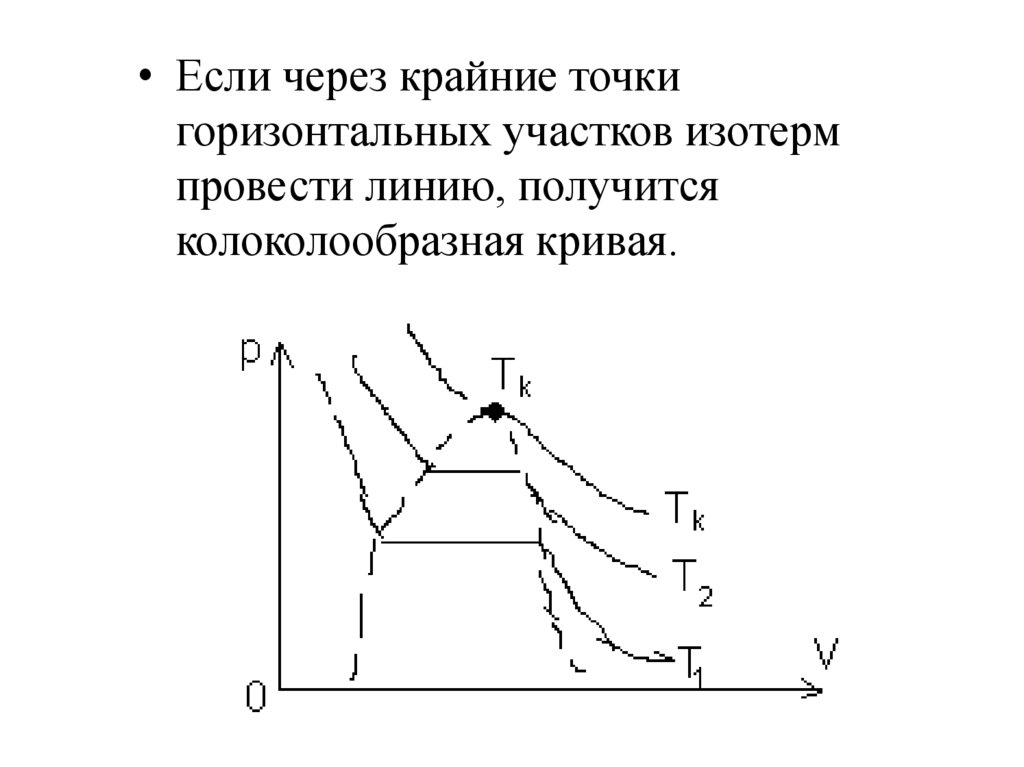
• Если через крайние точки
горизонтальных участков изотерм
провести линию, получится
колоколообразная кривая.

30.

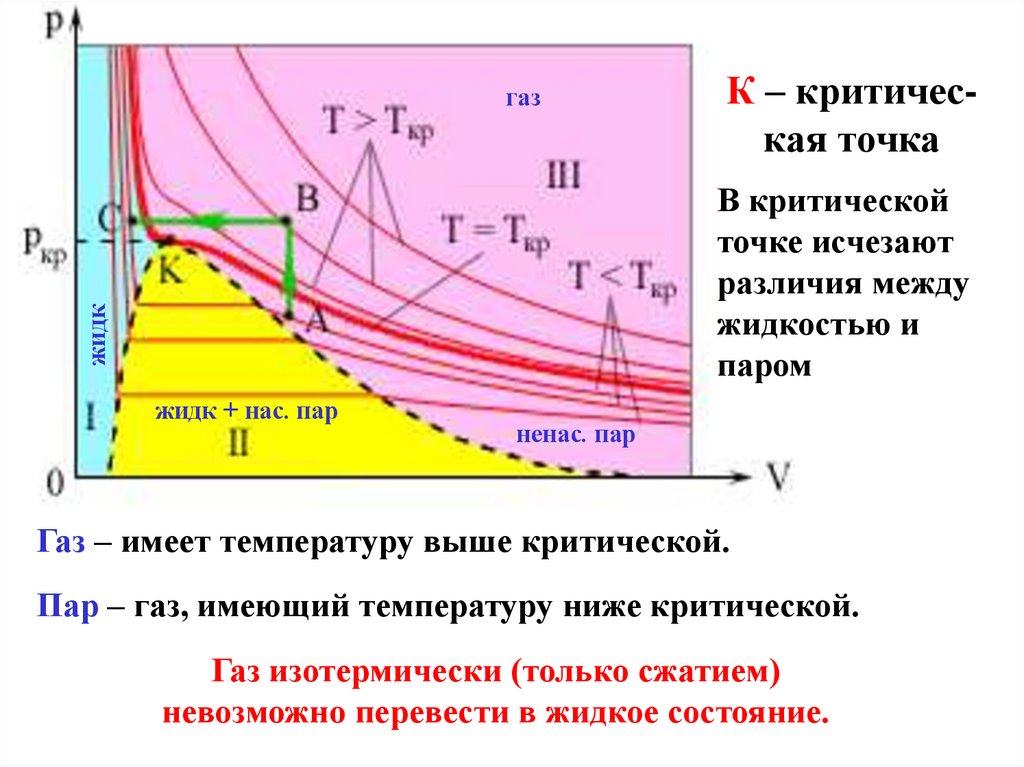
газ
К – критическая точка
жидк
В критической
точке исчезают
различия между
жидкостью и
паром
жидк + нас. пар
ненас. пар
Газ – имеет температуру выше критической.
Пар – газ, имеющий температуру ниже критической.
Газ изотермически (только сжатием)
невозможно перевести в жидкое состояние.

31.

• Соблюдая должные предосторожности,
можно получить состояния,
соответствующие начальным участкам
завитка на изотерме В-д-В (АВ и DE). Эти
участки соответствуют малоустойчивым
метастабильным состояниям. DE –
пересыщенный пар. Конденсация
насыщенных паров требует наличия
центров конденсации, роль которых могут
играть пылинки. АВ – Перегретая
жидкость. Процесс парообразования в
толще жидкости требует наличия центров
парообразования, роль которых могут
играть пылинки.

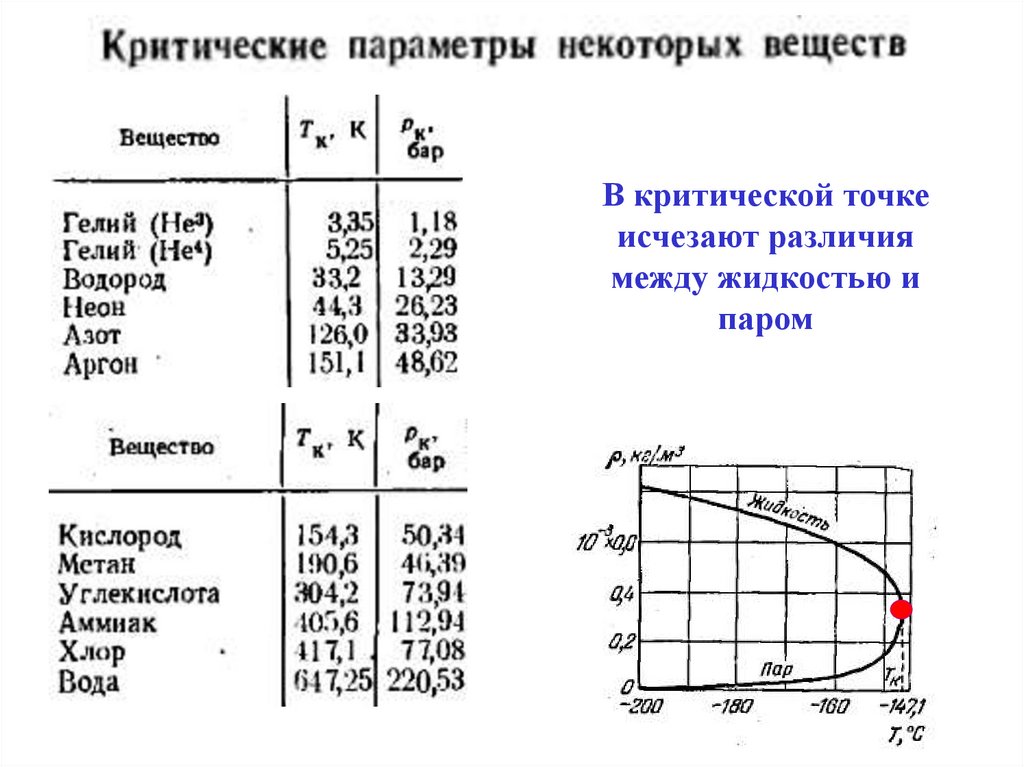
32.

В критической точке
исчезают различия
между жидкостью и
паром