Физика МКТ и термодинамика

1. Физика МКТ и термодинамика

Дальневосточный федеральный университет
Физика
МКТ и термодинамика
Распределения
Осьмушко Иван Сергеевич

2. Случайные величины и функция распределения

Модель случайного распределения с усреднением по
большому количеству частиц (доска Гальтона).

3. Основные понятия теории вероятностей

4. Основные понятия теории вероятностей

Рi - вероятность данного случайного события (измерения последовательные)
Важным условием математической вероятности является условие нормировки

5. Основные понятия теории вероятностей

6. Основные понятия теории вероятностей

Рассмотрим вероятности событий, принимающих непрерывный ряд
значений в заданной области. Вводится следующее понятие плотности
вероятности. (например, какова вероятность для молекулы иметь скорость в
интервале
P(v , v ) lim N
N (v )
N
Введем функцию, которую назовем плотностью вероятности
f(v ) lim v 0
P(v , v ) dP
v
dv
dP (v, v ) f(v )dv
v2
P f(v )dv
v1
Условие нормировки будет выглядеть
P f(v )dv 1
-

7.

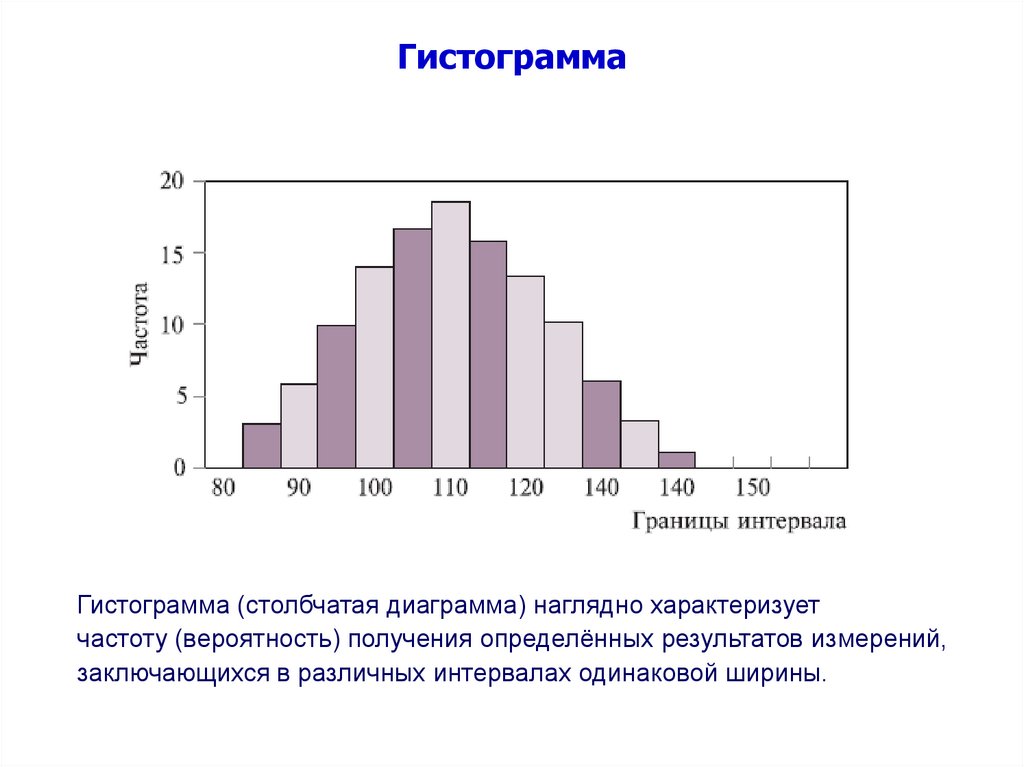
Гистограмма
Гистограмма (столбчатая диаграмма) наглядно характеризует
частоту (вероятность) получения определённых результатов измерений,
заключающихся в различных интервалах одинаковой ширины.

8.

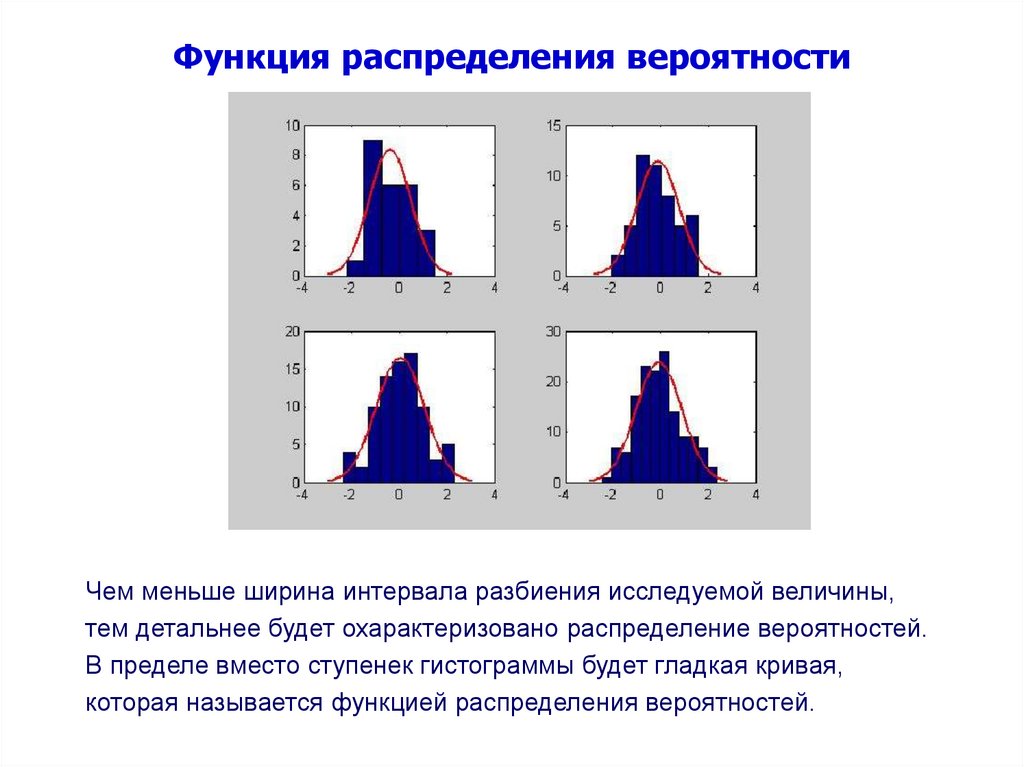
Функция распределения вероятности
Чем меньше ширина интервала разбиения исследуемой величины,
тем детальнее будет охарактеризовано распределение вероятностей.
В пределе вместо ступенек гистограммы будет гладкая кривая,
которая называется функцией распределения вероятностей.

9. Средние значения

Функция распределения f(x) позволяет определить среднее значение x.
Пусть результат измерений, лежащий в интервале от x до x+dx,
будет получен в ходе dNx измерений. Причем, dNx=NdPx; N – общее число измерений;
dPx=dNx/N – вероятность того,
что результат измерений будет лежать в интервале от x до x+dx.
Сумма всех результатов в ходе dNx измерений
будет равен xdNx=xNdPx.
Сумма всех возможных результатов в
конечном интервале от x1 до x2:
x2
x2
xdN xNdP .
x
x1
Разделив сумму на число измерений N,
получим среднее значение величины x:
Среднее значение некоторой произвольной
функции u(x) можно вычислить по формуле
x
x1
x2
x2
x1
x1
xc xdPx xf ( x)dx.
x2
uc u ( x) f ( x)dx;
x1

10.

Эргодическая гипотеза
Микроканонический ансамбль —
статистический ансамбль макроскопической
изолированной системы с постоянными
значениями объёма, числа частиц и энергии E.
Постулат о равновероятности
заключается в утверждении, что
все микросостояния данной
термодинамической системы равновероятны.
Микроскопические состояния меняются со временем. Точные определения
состояний по времени затруднены либо невозможны, либо не имеют смысла.
Вместо этого можно представить весь набор возможных состояний в виде
микроканонического ансамбля и усреднять по его состояниям.
Эргодическая гипотеза заключается в утверждении, что результат усреднения по
времени и по состояниям одинаков.

11. Распределение Больцмана (частиц по величинам потенциальной энергии)

12.

Барометрическая формула
Выделим в атмосфере вертикальный столб
с площадью поперечного сечения S .
Атмосферное давление на некоторой высоте h
обусловлено весом вышележащих слоёв воздуха.
Поэтому убыль давления при переходе от h к
h dh
обусловлена весом воздуха слоя dh :
dm g
dp
; dm Sdh dp gdh,
S
где
– плотность воздуха на высоте h.
Плотность воздуха вычислим из уравнения Менделеева-Клапейрона
PV
V
M
RT
pM
RT
Mpg
dp
dh.
RT
Мы получили дифференциальное уравнение, описывающее изменение
давления атмосферы с высотой над поверхностью Земли.

13.

Барометрическая формула
Дифференциальное уравнение, описывающее распределение
давления, будем решать методом разделения переменных:
Mpg
dp
dh
RT
dp
Mg
dh.
p
RT
Чтобы проинтегрировать это уравнение необходимо знать,
как температура меняется с высотой.
Для модели изотермической атмосферы, то есть для простейшего случая,
когда температура не изменяется с высотой, интегрирование даёт:
Mgh
ln p
ln C
RT
Mgh
exp(ln p ) exp(
ln C )
RT
Mgh
Mgh
).
p C exp(
), h 0 p(0) p0 C p p0 exp(
RT
RT

14.

Распределение Больцмана
Перепишем барометрическую формулу для изотермической атмосферы,
выразив молярную массу газа
через массу одной молекулы
M
m0 ,
а давление газа
p, p0 через его концентрацию n, n0 :
Mgh
p p0 exp(
); p nkT ; p0 n0 kT ; M m0 N A
RT
m0 N A gh
nkT n0 kT exp(
)
kN AT
Из полученной формулы следует, что
с понижением температуры число частиц
на высотах отличных от нуля, убывает,
обращаясь в нуль при T 0.
При абсолютном нуле все молекулы
расположились бы на земной поверхности.
Чем выше температура тем плавнее
концентрация молекул убывает с высотой.
m0 gh
n n0 exp(
).
kT
T2 T1

15.

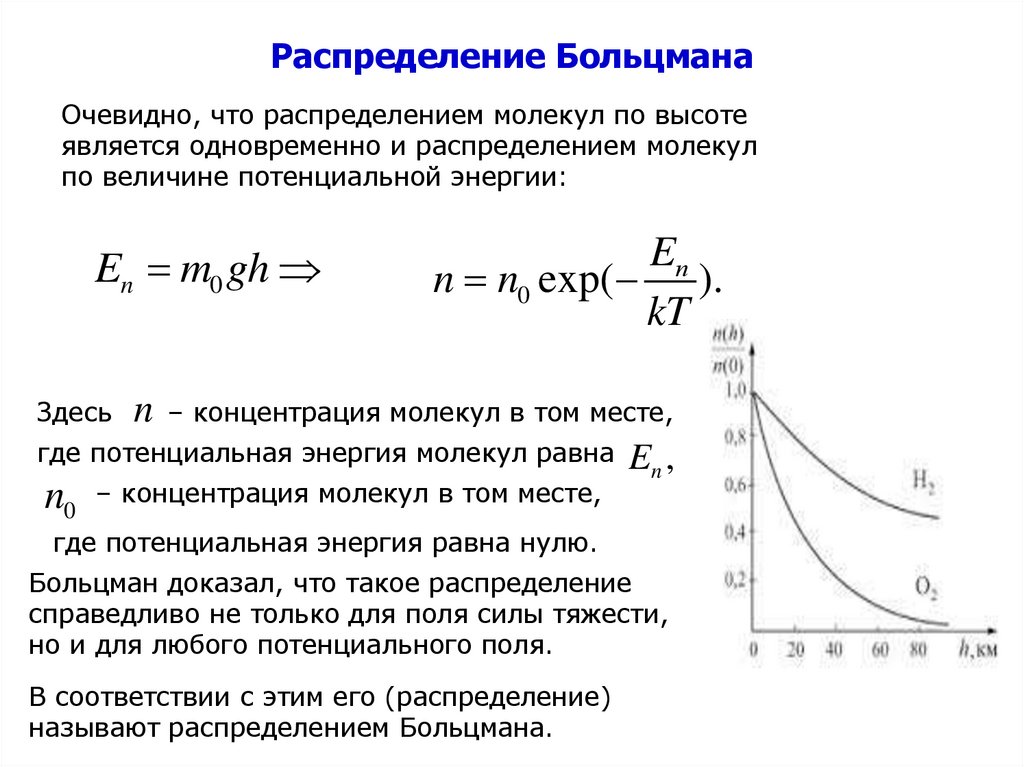
Распределение Больцмана
Очевидно, что распределением молекул по высоте
является одновременно и распределением молекул
по величине потенциальной энергии:
En m0 gh
Здесь
Eп
n n0 exp( ).
kT
n – концентрация молекул в том месте,
где потенциальная энергия молекул равна E ,
n0 – концентрация молекул в том месте,
n
где потенциальная энергия равна нулю.
Больцман доказал, что такое распределение
справедливо не только для поля силы тяжести,
но и для любого потенциального поля.
В соответствии с этим его (распределение)
называют распределением Больцмана.

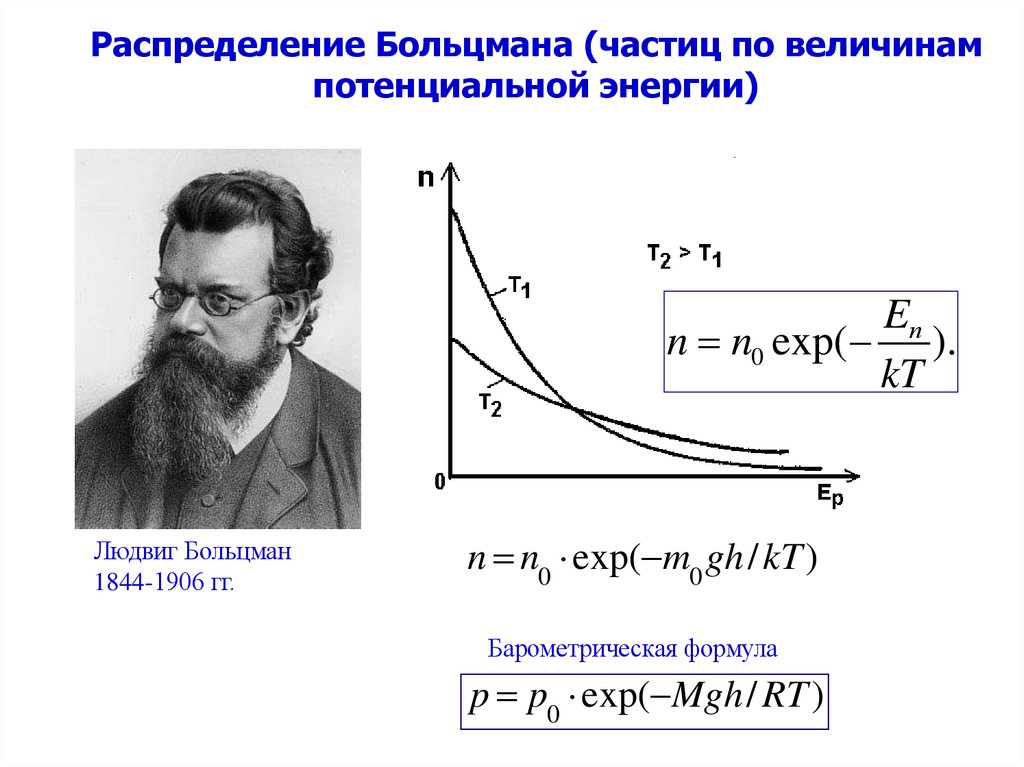
16.

Распределение Больцмана (частиц по величинам
потенциальной энергии)
Eп
n n0 exp( ).
kT
Людвиг Больцман
1844-1906 гг.
n n0 exp( m0 gh / kT )
Барометрическая формула
p p0 exp( Mgh / RT )

17.

Распределение Максвелла
(молекул по скоростям)

18. Распределение молекул по скоростям (Максвелла)

dn (v )
f(v )
n dv
P f(v )dv 1
Джеймс Клерк Максвелл
1831-1879 гг.
m0
f(v ) 4
2 kT
3/ 2
v 2 exp( m0v 2 / 2kT )

19.

Вывод распределения Максвелла
0. На основании эргодической гипотезы.
1. Ставится вопрос о нахождении числа частиц в интервале скоростей.
2. Огромное, но конечное число частиц, в диапазоне до бесконечно
больших значений скорости.
3. На основе закона сохранения энергии в поле тяготения.
4. Число частиц в единице объёма n.

20.

Вывод распределения Максвелла
Число частиц в единице объёма, обладающих скоростями в диапазоне v
вблизи скорости v:
Функция распределения показывает долю
скоростями, в единичном интервале вблизи v:
частиц
обладающих
Переходим к пределу с условием, что в каждом диапазоне большое число
частиц:
Левая часть – это вероятность, f(v) – плотность вероятности.

21.

Распределение по компонентам скорости
Рассмотрим слой газа на высоте z единичной
площади и запишем закон сохранения энергии:
Рассмотрим число частиц, пересекающих слой снизу и сверху:

22.

Распределение по компонентам скорости
При равновесии:
Разделим на nz0 и используем распределение Больцмана:
Продифференцируем закон сохранения энергии:

23.

Распределение по компонентам скорости
Заменим в левом интеграле и поменяем пределы интегрирования:
Следует:
Это равенство выполняется при условии (из закона сохранения
энергии):
Т. о. функция распределения:

24.

Распределение по компонентам скорости
Используем условие нормировки и найдём A.

25.

Распределение по компонентам скорости
Физический смысл A – это доля
молекул, обладающих околонулевыми
значениями одной компоненты
скорости.

26.

Распределение по скоростям
Найдём произведение вероятностей иметь три компоненты в
определённых диапазонах скоростей.

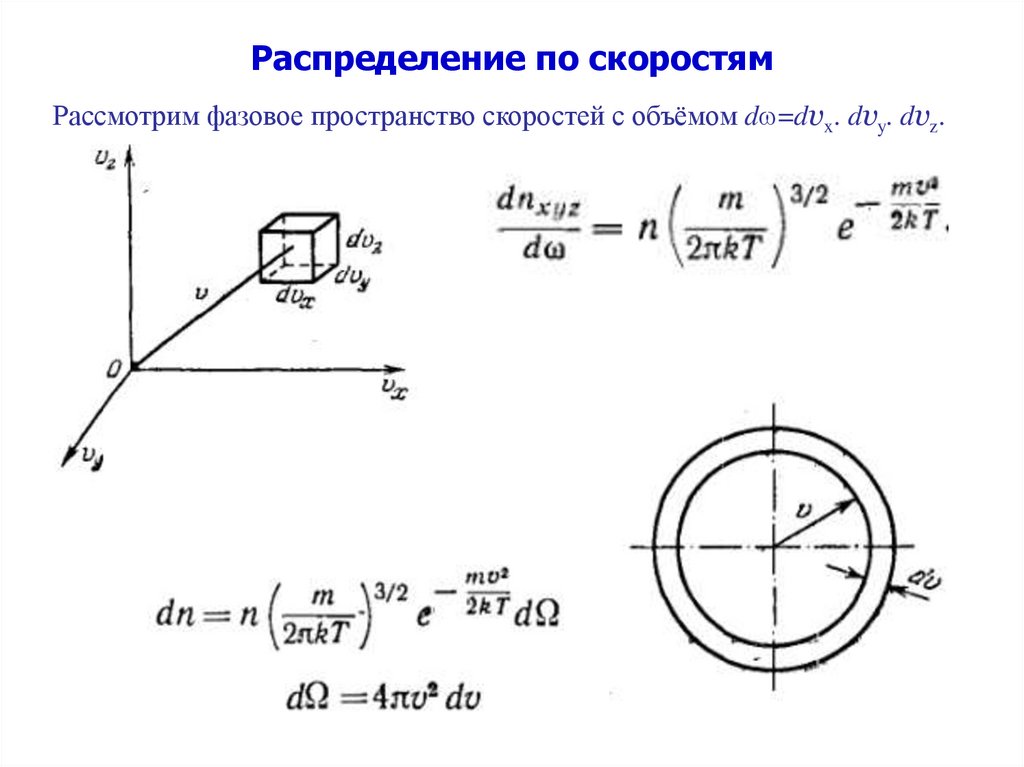
27.

Распределение по скоростям
Рассмотрим фазовое пространство скоростей с объёмом d =dvx. dvy. dvz.

28.

Распределение по скоростям
Определяет долю молекул единицы объема газа, скорости
которых заключены в интервале скоростей, равном единице,
включающем данную скорость.

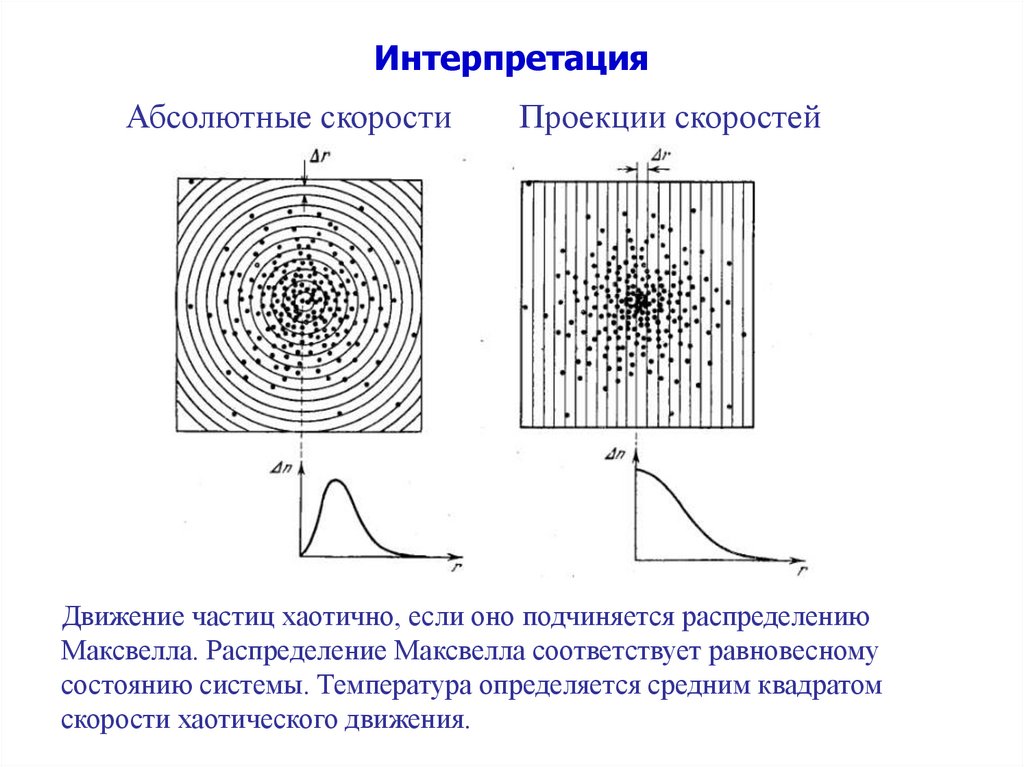
29.

Интерпретация
Абсолютные скорости
Проекции скоростей
Движение частиц хаотично, если оно подчиняется распределению
Максвелла. Распределение Максвелла соответствует равновесному
состоянию системы. Температура определяется средним квадратом
скорости хаотического движения.

30.

Наиболее вероятная скорость
Наиболее вероятной называют такую
скорость молекул vн, для которой
функция распределения f(v) принимает
максимальное значение, т.е. f ’(vн)=0.
Минимумы:
Максимум:

31.

Средняя арифметическая скорость
Средняя арифметическая скорость равна
отношению суммы всех скоростей всех молекул в
единице объема к числу молекул в единице объема.

32.

Средняя квадратичная скорость
Средняя квадратичная скорость молекул vкв это отношение суммы
квадратов скоростей молекул единицы объема к числу молекул в этом
объеме.

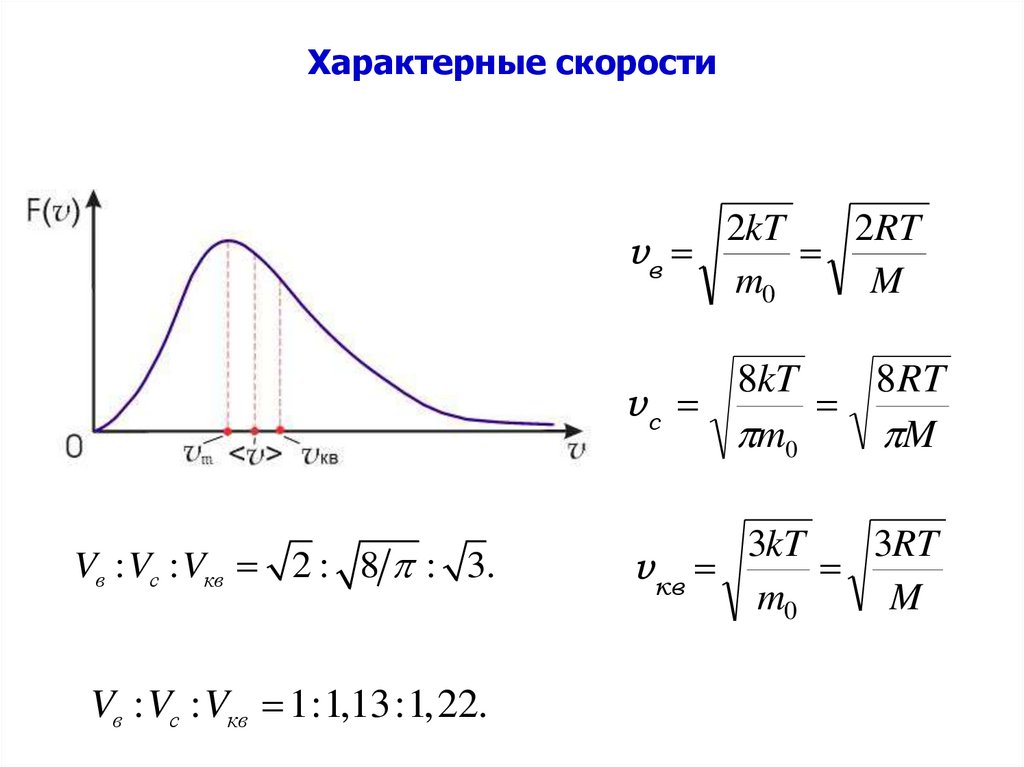
33. Характерные скорости

2kT
2RT
vв
m0
M
8kT
8RT
vс
m0
M
Vв : Vc : Vкв 2 : 8 : 3.
Vв : Vc : Vкв 1:1,13:1,22.
3kT
3RT
vкв
m0
M

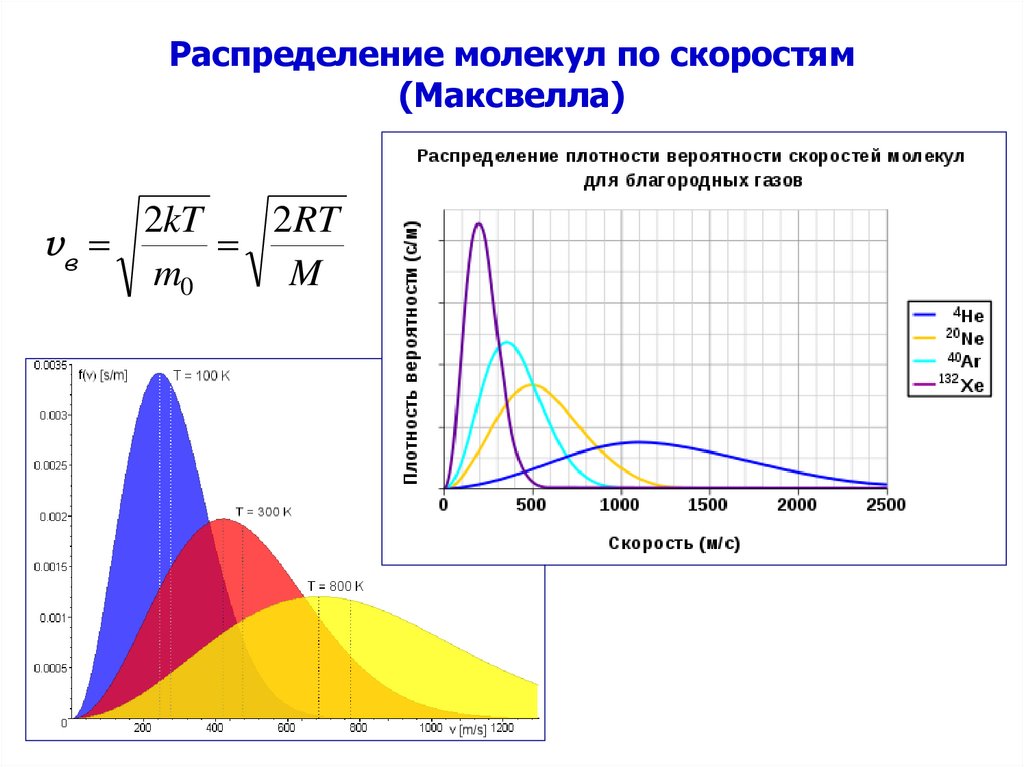
34. Распределение молекул по скоростям (Максвелла)

2kT
2RT
vв
m0
M

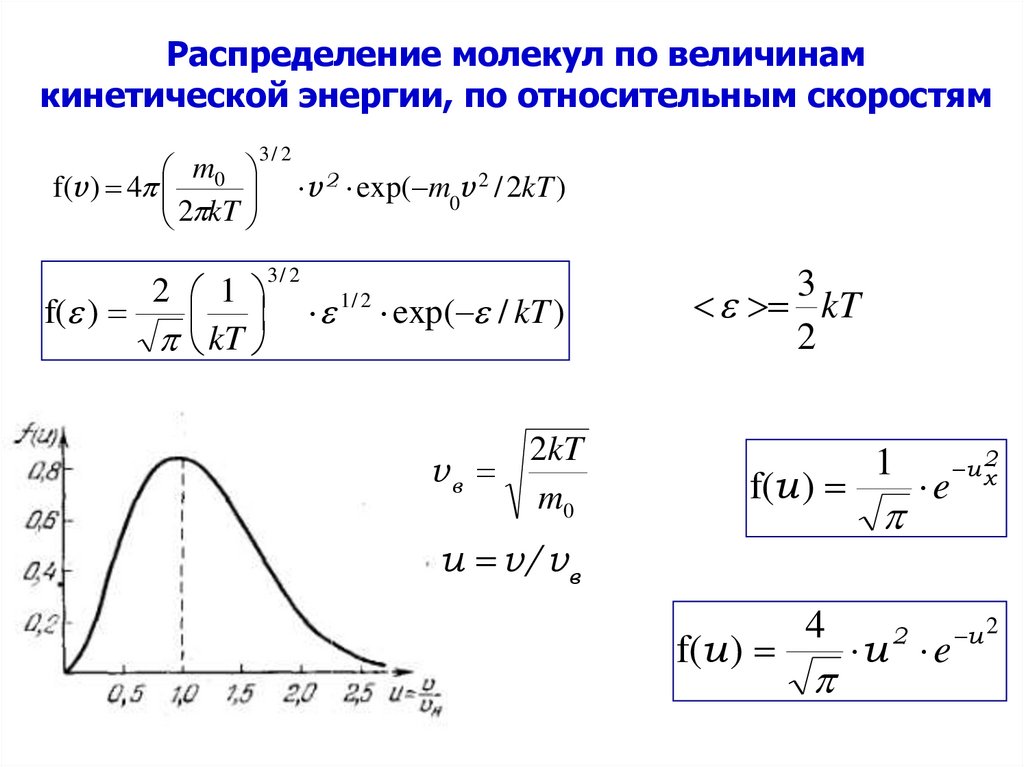
35. Распределение молекул по величинам кинетической энергии, по относительным скоростям

m
f(v ) 4 0
2 kT
3/ 2
2 1
f( )
kT
v 2 exp( m0v 2 / 2kT )
3/ 2
1/ 2
exp( / kT )
2kT
vв
m0
3
kT
2
f(u )
u v/v в
f(u )
4
1
2
e
u e
2
u x
u 2