Основные уравнения техники СВЧ

1.

2.

Наиболее общий подход к явлениям
электродинамики на низких, высоких и
сверхвысоких частотах обеспечивается
применением теории электромагнитного поля и
уравнений Максвелла.
С учетом движущихся свободных зарядов система
уравнений Максвелла относительно векторов
напряженностей электрического и магнитного
полей Е и Н, а также векторов индукции D и В
может быть записана в виде

3.

Через ε,μ и σ здесь, как обычно, обозначены относительные
диэлектрическая и магнитная проницаемости среды и ее
удельная проводимость. Поскольку рабочей средой в
электровакуумных приборах является вакуум или газ,
величины ε и μ, могут быть в дальнейшем положены равными
единице, а удельная проводимость среды σ — равной нулю.

4.

Величины диэлектрической и магнитной проницаемостей вакуума ε0 и μ0 равны
Через ρ и V в уравнениях (2.1) и (2.3) обозначены объемная плотность
свободных зарядов и скорость движения этих зарядов. Величина ρV
определяет плотность конвекционного тока «JКОНВ (тока переноса):
Jконв= ρV
(2.8)
и характеризует количество электрического заряда, проходящего за
единицу времени через единицу поверхности, нормальной к вектору
скорости V. Полная плотность тока Jполн входящая в (2.1), в любом
сечении при σ = 0 является суммой плотностей конвекционного тока и
тока смещения.

5.

Система уравнений Максвелла является неполной для решения задач при наличии
свободных заряженных частиц, поскольку скорость V зависит не только от начальных
условий, но и от напряженностей полей Е и Н в каждой точке, где находится
рассматриваемая частица.
Зависимость скорости заряженных частиц от величин электрического и магнитного
полей определяется уравнением движения, которое с учетом силы Лоренца
может быть записано в общем виде:
где q — заряд частицы, предполагаемый здесь точечным,
т — масса частицы и F — сила, действующая на заряд.
В наиболее распространенном случае, когда рассматриваемыми зарядами являются
свободные электроны, необходимо положить q = -е. Абсолютная величина заряда
электрона и величина массы покоящегося электрона равны:

6.

Величины е и m0 часто встречаются в конкретных расчетах электронных приборов*.
Уравнение движения широко используется при анализе и расчете
различных электронных приборов СВЧ. Напряженность электрического поля Е и индукция магнитного поля В, входящие в (2.10), могут
быть как постоянными во времени, так и иметь переменную
составляющую. Практически, однако, в большинстве случаев достаточно учитывать, кроме постоянных составляющих Е и В, лишь
переменную составляющую электрического поля, пренебрегая высокочастотной составляющей магнитного поля. Для иллюстрации
рассмотрим участок передающей линии, возбужденной на поперечной электромагнитной волне (волне типа ТЕМ). Положим для простоты постоянные во времени поля равными нулю. Силу, действующую
на свободный электрон при вакуумном наполнении, можно записать
в виде
F = -eE - eμo [vH] = FE + FH
,где FЕ и FН — составляющие, обусловленные действием
электрического и магнитного высокочастотных полей.

7.

Отношение |Н|/|Е| является обратной величиной характеристического сопротивления ,
равного в рассматриваемом случае
Похожий результат можно получить и в других случаях, например, при движении
заряда в волноводе или полом резонаторе. Таким образом, если скорость электронов
много меньше скорости света в свободном пространстве, то действием
высокочастотного магнитного поля в сравнении с действием высокочастотного
электрического поля можно обычно пренебречь. Далее будет показано, что условие
малости скорости электронов в сравнении со скоростью света выполняется в
большинстве современных приборов СВЧ. Однако и в тех случаях, когда эти скорости
оказываются соизмеримыми, от действия высокочастотного магнитного поля удается,
как правило, отвлечься, так как в пространстве взаимодействия обычно присутствует
преимущественно электрическое поле.

8.

Уравнение непрерывности вытекает непосредственно из уравнений
Максвелла. Рассмотрим выражение плотности полного тока
По уравнению (2.1) полный ток всегда имеет чисто вихревой характер, поэтому
Подставляя в это выражение уравнение (2.3), получаем уравнение непрерывности в виде
Уравнение (2.13) особенно полезно при рассмотрении волновых процессов в
электронных потоках, например, в лампах бегущей и обратной волны.

9.

Для вычисления скорости электрона, приобретенной в потенциальном электрическом
поле, обычно исходят из закона сохранения энергии
Уравнение может быть переписано в виде

10.

Время пролета
Важным параметром, характеризующим электронные приборы сверхвысоких частот,
является время пролета электрона τ между двумя заданными электродами лампы,
например, между катодом и анодом в диоде, между катодом и сеткой в триоде, между
двумя сетками в многосеточной лампе или в клистроне и т. д.
Время пролета электрона, как и любой другой материальной частицы, может быть
определено интегрированием соответствующего уравнения движения. Если известны
напряженности полей Е и Н, а также заданы начальные условия, то интегрирование
уравнения (2.10) по времени позволяет вычислить скорость электрона в любой точке
пролетного пространства. Дальнейший расчет времени пролета может быть сведен к
нахождению интеграла вида
где S1 и S2 — координаты рассматриваемых электродов.

11.

Другой очевидный метод расчета времени пролета сводится к повторному
интегрированию уравнения (2.10) и нахождению уравнения движения электрона в
виде s = f(t). Подставляя поочередно в полученное уравнение координаты
рассматриваемых электродов S1 и S2, можно найти интересующее нас время пролета
τ, как разность соответствующих времен t1 и t2
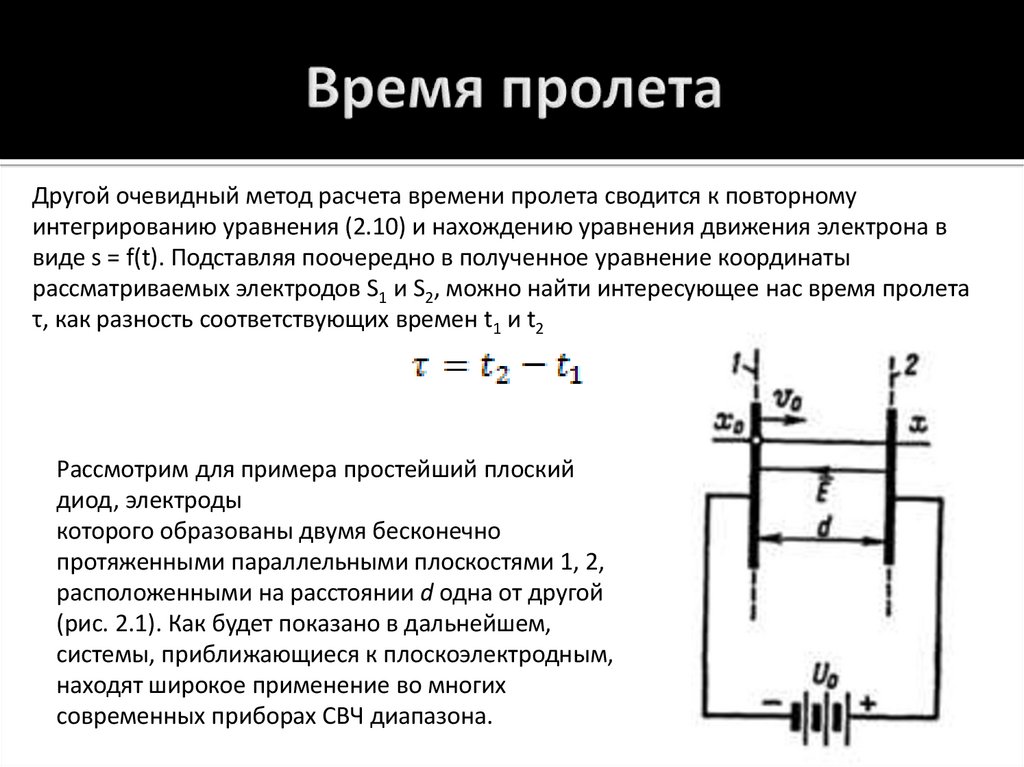
Рассмотрим для примера простейший плоский
диод, электроды
которого образованы двумя бесконечно
протяженными параллельными плоскостями 1, 2,
расположенными на расстоянии d одна от другой
(рис. 2.1). Как будет показано в дальнейшем,
системы, приближающиеся к плоскоэлектродным,
находят широкое применение во многих
современных приборах СВЧ диапазона.

12.

Напряжение U0 будем считать постоянным во времени; внешнее магнитное поле
положим равным нулю. Релятивистских поправок учитывать не будем, считая
Уравнение движения (2.10) в данном случае при отсутствии пространственного
заряда имеет простейший вид:
При интегрировании уравнения движения используем следующее начальное условие:
в плоскости х = х0 при t= t0 скорость электрона равна v0

13.

При (случай, близкий к обычному диоду с накаленным катодом) получаем простое
уравнение, определяющее время пролета в режиме насыщения диода:
Для электроники СВЧ представляет интерес и другой случай, когда (U0 = 0), но
начальная скорость электронов отлична от нуля. Подобная ситуация встречается,
например, в клистронах, где электроны, поступающие в плоский зазор через
отверстия в первом электроде, двигаются далее по инерции. Время пролета через
такой зазор равно

14.

Перейдем к обсуждению времени пролета в случае, когда между электродами
плоского зазора приложено переменное напряжение (рассмотрение
несинусоидального напряжения практического интереса для диапазона СВЧ пока не
представляет).

15.

Абсолютная величина времени пролета сама по себе недостаточно полно
характеризует влияние инерции электронов на работу прибора. Как указывалось во
введении, поведение электронного прибора в значительной степени зависит от того,
является ли время пролета соизмеримым с периодом колебания. Поэтому более
важным является отношение времени пролета к периоду колебаний T, т. е. величина
С физической точки зрения угол пролета показывает изменение фазы напряжения,
приложенного к рассматриваемым электродам, за время движения электрона между
этими электродами. Зная время пролета и рабочую частоту, нетрудно вычислить угол
пролета электронов. Так, в случае рассматривавшегося выше плоского зазора при
исчезающем малом переменном напряжении, наложенном на большое постоянное
напряжение, т. е. при Uт << U0, невозмущенный угол пролета
электронов при отсутствии пространственного заряда равен