NumPy. Анализ данных

1.

NumPy
Анализ данных

2.

О пакете
NumPy предназначен для выполнения научных вычислений и
активно используется не только в качестве самостоятельной
библиотеки учеными и преподавателями по всему мирую

3.

Подключение пакета
• import numpy as np
• Если пакет не установлен, то необходимо в
терминале (Alt+F12) выполнить команду:
• pip install numpy
• Причины популярности пакета: скорость его работы; простой и
продуманный синтаксис; богатство возможностей библиотеки,
начиная с базовых математических функций и заканчивая
работой с полиномами, линейной алгеброй и многомерными
матрицами (тензорами)

4.

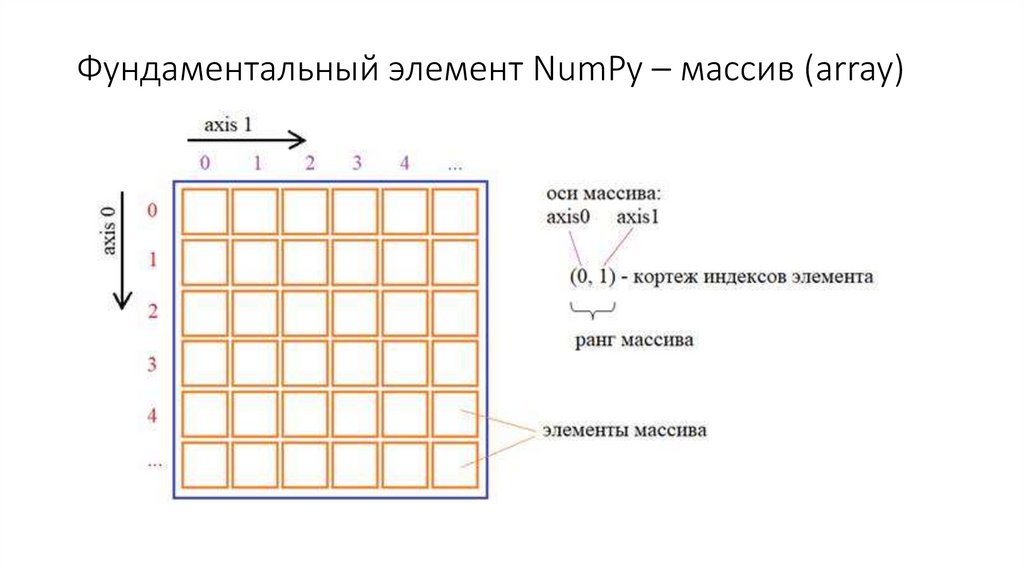
Фундаментальный элемент NumPy – массив (array)

5.

Фундаментальный элемент – однородный многомерный массив
• В NumPy элементы массива имеют единый тип данных.
Их индексы описываются кортежем целых
неотрицательных чисел. Размерность кортежа – это ранг
массива (то есть, размерность массива), а каждое число в
кортеже представляет свою отдельную ось.
• в самом простом варианте можно создать одномерный
массив так:
• a = np.array([1, 2, 3, 4])
• Смешение типов в рамках одного массива не
допускается.

6.

что такого в массивах NumPy
• Предположим, мы определили одномерный массив с числами от 1 до 9:
• a = np.array([1,2,3,4,5,6,7,8,9])
• Обращение к элементу массива: a[0]
• Предположим, нам понадобилось представить одномерный массив a в виде
матрицы 3х3. Меняем его размерность:
• b = a.reshape(3, 3)
• и получаем результат:
• array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
• Далее, можем обращаться к элементам матрицы b так: b[1][2] или так: b[1, 2]

7.

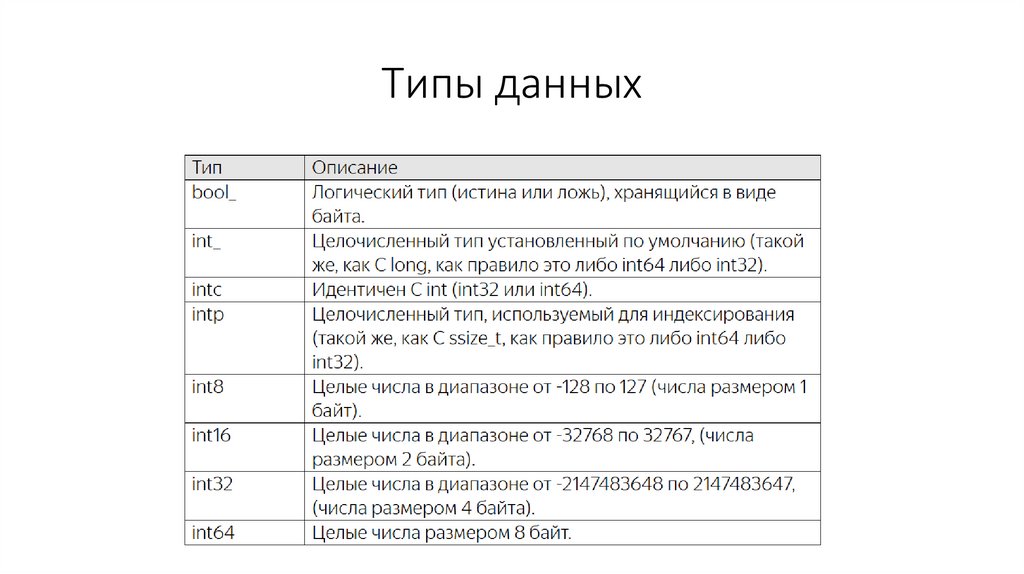
тип элементов массива
• Если нам явно нужно указать тип элементов массива, то
его можно записать вторым аргументом, например, так:
• a = np.array([1,2,3,4], 'float64')
• В результате все величины будут вещественными 64битными числами. И здесь сразу возникает вопрос: какие
типы данных поддерживает пакет NumPy. Их огромное
количество и посмотреть можно с помощью словаря
sctypeDict:
• np.sctypeDict

8.

Типы данных

9.

Функции автозаполнения, создания матриц
• мы можем все это сделать также через функцию array, используя
механизм генерации списков, например, так:
• np.array( [0]*10 ) # массив из 10 нулей
• np.array( [1]*15 ) # массив из 15 единиц
• np.array( [x for x in range(10)] ) # массив из чисел от 0 до 9
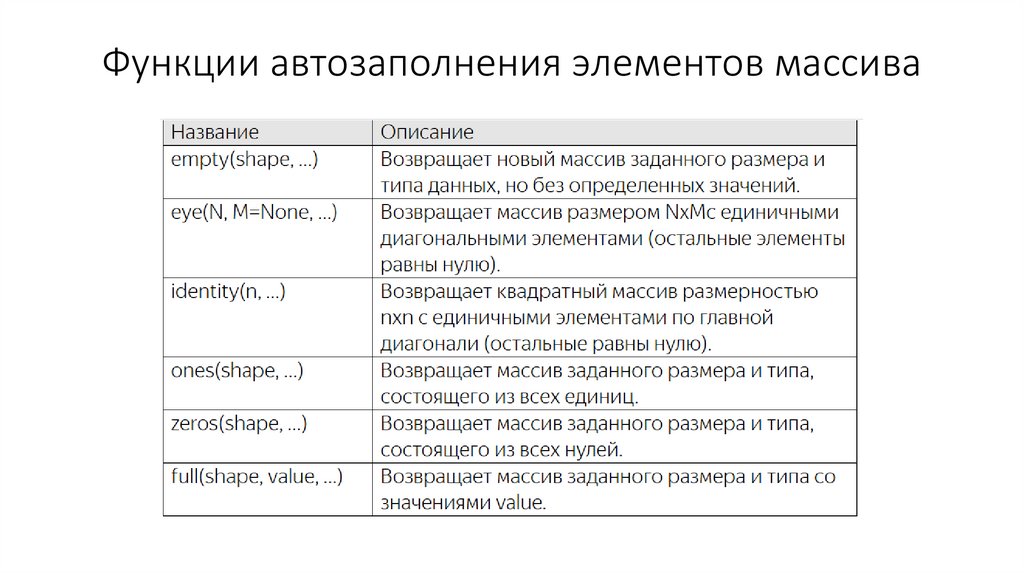
• Но есть более быстрые способы (по скорости выполнения)
создания подобных массивов. Для этого в NumPy имеются
полезные функции.

10.

Функции автозаполнения элементов массива

11.

примеры
• Например, так:
• np.empty(10) # создание одномерного массива с произвольными
числами
• np.empty(10, dtype='int16')
• np.empty((3, 2), dtype='float32') # возвращает матрицу 3x2 с типом
float32
• Для функций eye и identity размерности указываются отдельными
параметрами:
• np.eye(4) # матрица 4х4
• np.eye(4, 2)
# матрица 4x2
• np.identity(5) # матрица 5x5

12.

примеры
• Функции ones, zeros и full работают по аналогии с функцией
empty:
• np.zeros( (2, 3, 4) ) # нулевая матрица размерностью 2x3x4
• np.ones( [4, 3], dtype='int8') # матрица 4x3 из единиц и типом int8
• np.full((3, 2), -1) # матрица 3x2, состоящая из -1
• Все эти функции работают быстрее, чем функция array с
генератором списков языка Python. Поэтому их предпочтительно
использовать при создании и инициализации массивов
определенными значениями.

13.

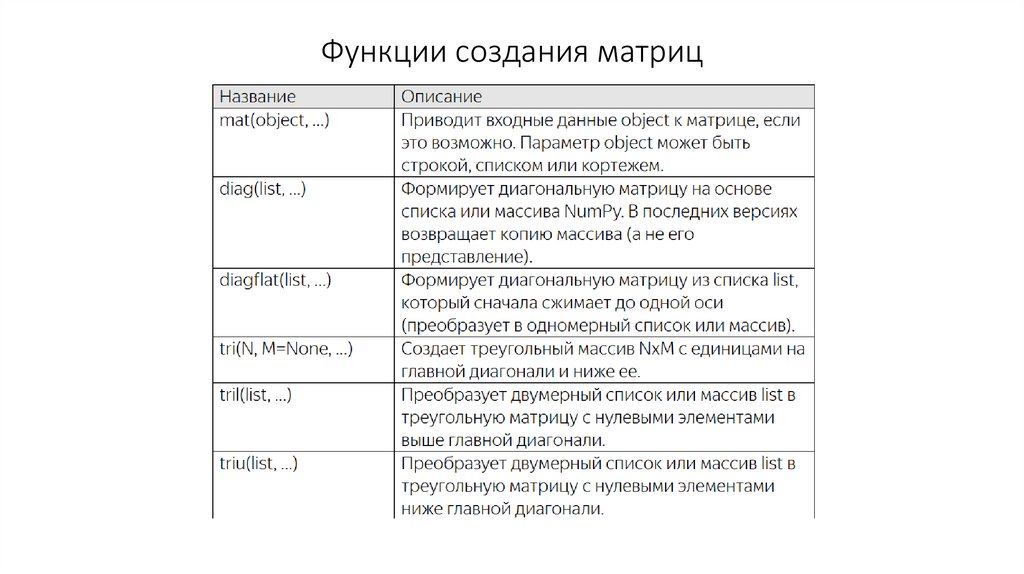
Функции создания матриц

14.

примеры
• Давайте посмотрим как работают эти функции.
• np.mat('1 2 3 4') # создает матрицу 1x4 из строки
• np.mat('1, 2, 3, 4') # то же самое: создает матрицу 1x4 из строки
• np.mat('1 2; 3 4') # возвращает матрицу 2x2
• Или же, вместо строк можно использовать список или кортеж:
• np.mat([5, 4, 3])
• np.mat( [(1,2,3), (4,5,6)])
• Но, если из переданных данных нельзя сформировать
прямоугольную таблицу (матрицу), то произойдет ошибка:
• np.mat( [(1,2,3), (4,5,6,7)])# ошибка, размерности не совпадают

15.

примеры
• Следующая функция позволяет формировать диагональные
матрицы:
• np.diag([1, 2, 3]) # диагональная матрица 3x3
• Но, если ей передать двумерный список, то она возвратит
одномерный массив из элементов, стоящих на главной
диагонали:
• np.diag([(1,2,3), (4,5,6), (7,8,9)]) # выделение элементов главной
диагонали

16.

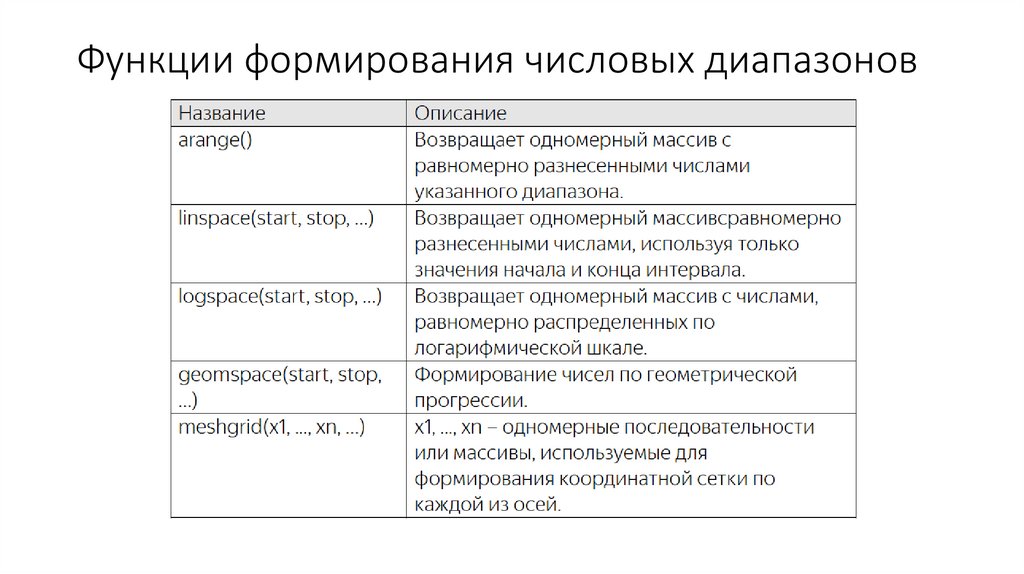
Функции формирования числовых диапазонов

17.

примеры
• Первая функция arrange довольно часто применяется в программах на
Python. Она позволяет проходить заданный интервал с указанным
шагом, например, так:
• np.arange(5)# интервал [0; 5) с шагом 1
• np.arange(1, 5)# интервал [1; 5) с шагом 1
• np.arange(1, 5, 0.5) # интервал [1; 5) с шагом 0,5
• Обратите внимание, в отличие от функции range языка Python в arrange
пакета NumPy можно указывать вещественные значения. Вот еще один
пример, демонстрирующий это:
• np.arange(0, np.pi, 0.1)
• Здесь все величины вещественные. Мы начинаем движение от
значения 0 с шагом 0,1 пока не дойдем до значения пи (не включая
его)

18.

примеры
• Похожим образом работает и функция linspace. Она разбивает
указанный интервал на равномерные отрезки и возвращает массив
этих значений:
• Мы указываем в качестве аргументов интервал [start; stop] и число
отметок в этом интервале n. Если n = 0, то получим пустой массив. При
n = 1 – значение start. При n = 2 – значения start и stop. При n> 2
равномерное разбиение интервала точками m = n-2. Например:
• np.linspace(0, np.pi, 0) # пустой массив
• np.linspace(0, np.pi, 1) # одно значение 0
• np.linspace(0, np.pi, 2) # два значения: 0 и pi
• np.linspace(0, np.pi, 3) # три значения: 0, pi/2, pi
• В чем отличие linspace от arange? В arange мы указываем сами шаг
движения по числовой оси. При этом число значений определяется
граничными значениями. А в linspace мы задаем граничные значения
и число делений, а шаг вычисляется автоматически.

19.

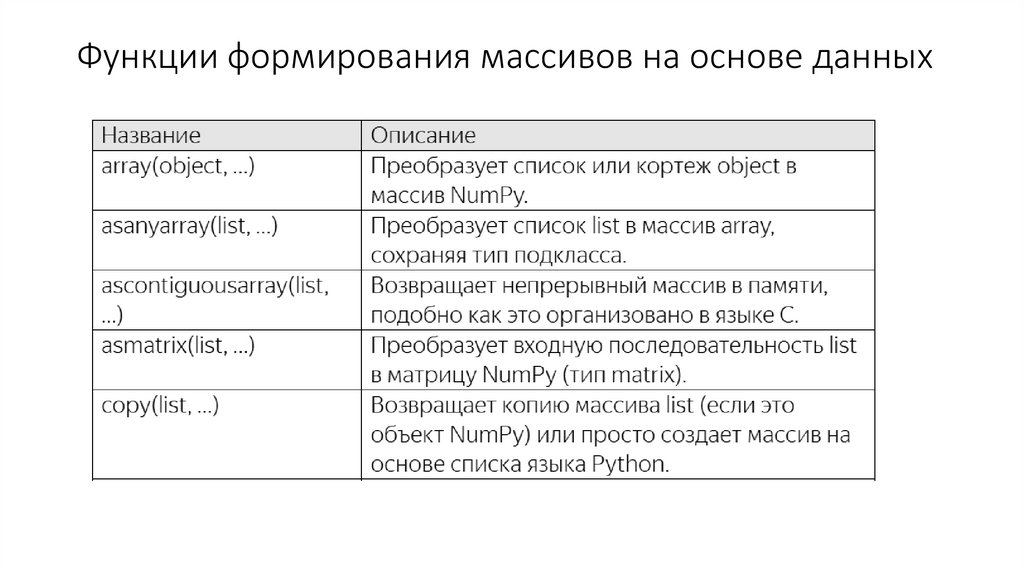
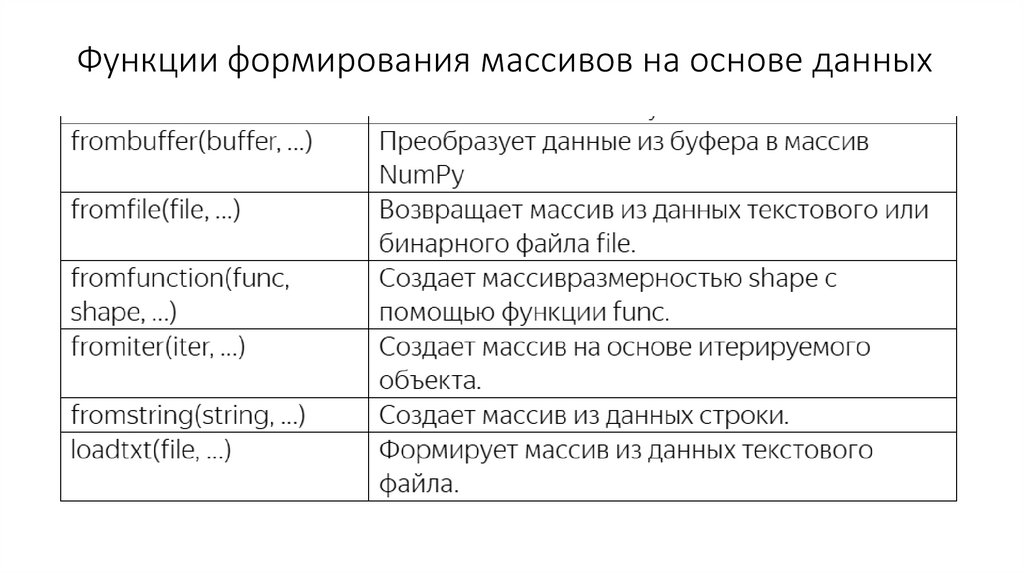
Функции формирования массивов на основе данных

20.

Функции формирования массивов на основе данных

21.

примеры
• Функция copy выполняет копирование массива.
Например, имеется массив:
• a = np.array( [(1, 2), (3, 4)] )
• И создать его копию в памяти устройства, можно так:
• b = np.copy(a)
• В этом легко убедиться, если вывести id этих объектов:
• print(id(a), id(b))

22.

примеры
• Формирование массива с помощью функции выполняется следующим
образом:
• def getRange(x, y):
• return 100*x + y
• a = np.fromfunction(getRange, (2, 2))
• print(a)
• Функция принимает два аргумента, т.к. формируется двумерная матрица
размерами 2x2. То есть, число аргументов функции равно размерности
матрицы и каждый аргумент соответствует индексу по своей оси. При
выполнении этой программы в консоли увидим результат:
• [[ 0. 1.]
• [100. 101.]]

23.

Размер массива
• если требуется узнать сколько байт занимает один
элемент, то можно воспользоваться свойством:
• a.itemsize # вернет 4 (байта)
• Соответственно, размер памяти для всего массива
можно вычислить так:
• a.size*a.itemsize # вернет 72 (байта)

24.

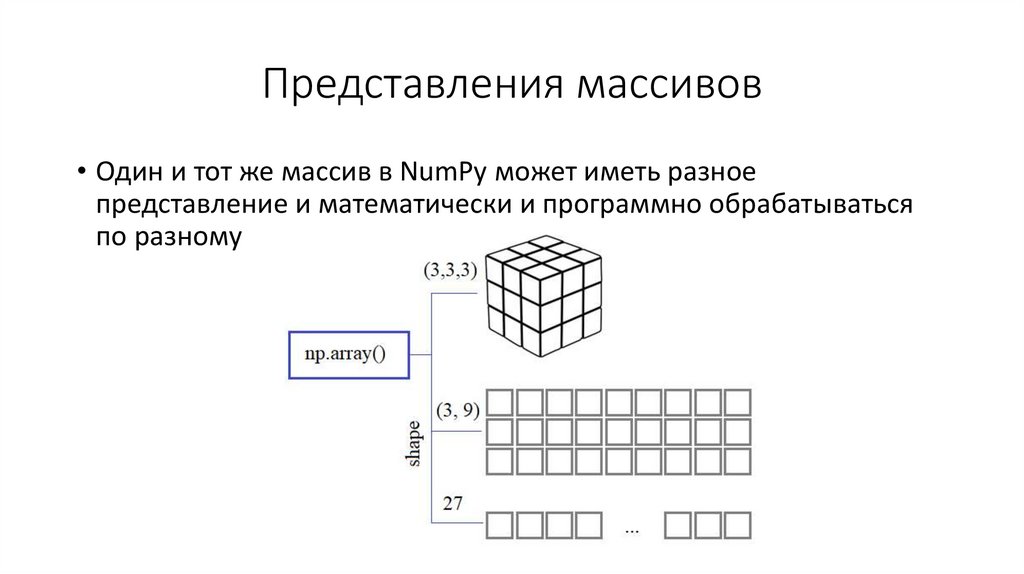
Представления массивов
• Один и тот же массив в NumPy может иметь разное
представление и математически и программно обрабатываться
по разному

25.

Метод view() для создания представления
• У каждого массива array существует метод view(), который возвращает копию
его представления. Предположим, мы присваиваем один массив другому:
• a = np.array([1,2,3,4,5,6,7,8,9])
• b=a
• Зная, что в языке Python переменные – это ссылки на объекты, то a и b будут
ссылаться на один и тот же массив, копирования здесь никакого происходить
не будет. Следовательно, если дальше по программе изменить форму
массива через одну из этих ссылок, например, так:
• a.shape = 3,3
• то вторая ссылка b также будет ссылаться на это измененное представление.
В больших и сложных проектах такое поведение может приводить к
неожиданным ошибкам, когда программист ожидает вектор, а получает
матрицу.

26.

Метод view() для создания представления
• Чтобы разрешить эту проблему достаточно создать новое
представление начального массива a с помощью метода view():
• a = np.array([1,2,3,4,5,6,7,8,9])
• b = a.view() # создание нового представления
• Тогда, меняя форму через ссылку a:
• a.shape = 3,3
• это уже никак не скажется на форме того же самого массива,
доступного через ссылку b:
• array([1, 2, 3, 4, 5, 6, 7, 8, 9])

27.

Создание копий массивов
• Иногда в программе все же нужно создавать копии массивов. Это
можно сделать несколькими способами. В последних версиях NumPy
функция array() возвращает копию переданного ей массива, например:
• a = np.array([1,2,3,4,5,6,7,8,9])
• b = np.array( a ) # создается копия массива
• Или же, копию можно получить с помощью метода copy объекта array:
• c = a.copy() # создание копии массива
• При этом происходит копирование всех свойств объекта array.
Последний вариант предпочтителен, когда нам нужно получить
полную копию массива, а не просто новый объект array.

28.

Изменение размерности массивов
• Предположим, у нас имеется массив, состоящий из десяти чисел:
• a = np.arange(10) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
• Для изменения формы этого массива, достаточно указать свойству shape
кортеж с новыми размерами, например, так:
• a.shape = 2, 5 # массив размерностью 2x5
• В результате изменится представление массива, на которое ссылается
переменная a. Если же требуется создать новое представление массива,
сохранив прежнее, то следует воспользоваться методом reshape():
• b = a.reshape(10) # массив [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
• Ссылки b и a будут использовать одни и те же данные, то есть, изменение
массива через b: b[0] = -1
• приведет к изменению соответствующего элемента массива a:
• array([[-1, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9]])

29.

Транспонирование матриц
• Например, если имеется матрица (двумерный массив):
• a = np.array([(1, 2, 3), (1, 4, 9), (1, 8, 27)])
• то операция транспонирования может быть реализована так:
• b = a.T
• Мы здесь создаем лишь новое представление тех же самых данных
массива a. И изменение элементов в массиве b:
• b[0, 1] = 10
• приведет к соответствующему изменению значения элемента и
массива a. Это следует помнить, используя операцию
транспонирования.

30.

Транспонирование векторов
• Предположим, имеется одномерный массив:
• x = np.arange(1, 10)
• и мы выполняем операцию транспонирования:
• x.T
• В результате ничего не изменилось: вектор как был строкой, так строкой и
остался. Дело в том, что массив x имеет только одну размерность, поэтому
здесь нет понятия строк и столбцов. Соответственно, операция
транспонирования ни к чему не приводит. Чтобы получить ожидаемый
эффект, нужно добавить к массиву еще одну ось, например, так:
• x.shape = 1, -1
• И теперь, при транспонировании получим вектор-столбец:
• x.T # вектор-столбец 9x1

31.

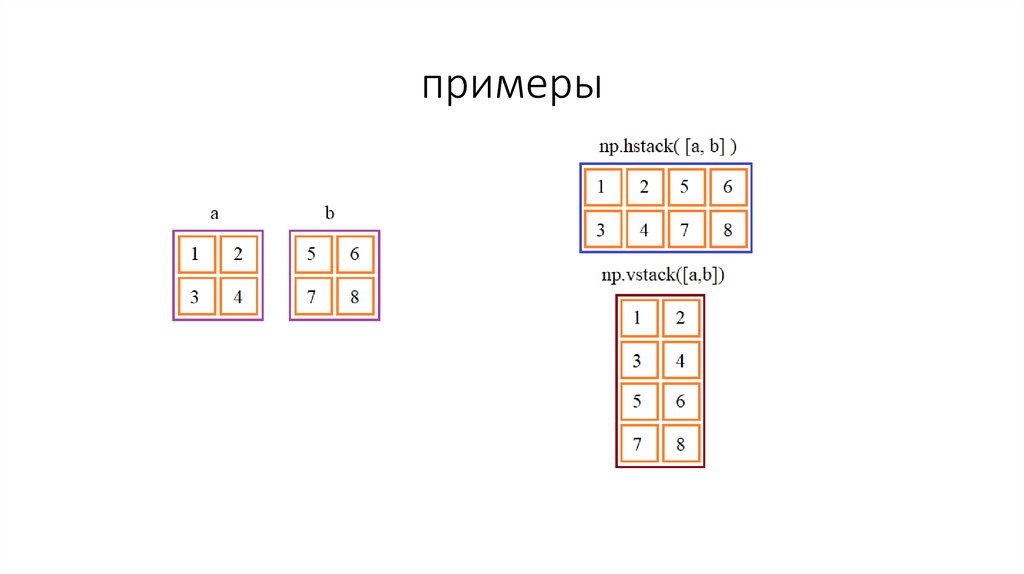
Объединение и разделение массивов
• Предположим у нас есть два двумерных массива:
• a = np.array([(1, 2), (3, 4)])
• b = np.array([(5, 6), (7, 8)])
• Их можно объединить как по горизонтали, так и по вертикали, с
помощью функций:
• np.hstack([a, b]) # объединение по оси axis1 (размерность 2x4)
• np.vstack([a, b]) # объединение по оси axis0 (размерность 4x2)

32.

примеры

33.

Объединение одномерных массивов
• Аналогичным образом происходит объединение и одномерных
массивов:
• a = np.fromstring('1 2 3 4', sep = ' ')
• b = np.fromstring('5 6 7 8', sep = ' ')
• И при выполнении: np.hstack([a, b])
• получим:
• array([1., 2., 3., 4., 5., 6., 7., 8.])
• А во втором случае: np.vstack([a, b])
• результатом будет двумерный массив:
• array([[1., 2., 3., 4.],
[5., 6., 7., 8.]])

34.

Разделение массивов
• Пусть имеется одномерный массив из 10 элементов:
• a = np.arange(10)
• И мы хотим разделить его на две равные части. Это реализуется с
помощью функции hsplit:
• np.hsplit(a, 2)
• которая возвращает список из двух массивов. Второй параметр 2
указывает число частей, на которые делится исходный массив.
Причем, деление выполняется по горизонтали. Если в нашем
примере указать 3 части, то возникнет ошибка.

35.

Разделение массивов
• Также ошибка будет и при разбиении этого массива по вертикали:
• np.vsplit(a, 2) # ошибка: нет вертикальной оси
• так как массив имеет одну горизонтальную ось. Чтобы вторая
функция сработала, преобразуем массив a в вектор столбец:
• a.shape = 10, -1 # вектор-столбец
• а, затем, разобьем по вертикали:
• np.vsplit(a, 2)
• На выходе получим два одномерных массива длиной 5
элементов.

36.

Индексация массивов, срезы
• Предположим, что имеется одномерный массив:
• a = np.arange(12) # array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])

37.

Индексация массивов, срезы
• Общий синтаксис срезов выглядит так:
• <имя массива>[start:stop:step]
• Примеры использования этой конструкции:
• b = a[2:4] # array([2, 3])
• Здесь указан начальный индекс 2, конечный индекс 4 и по умолчанию
берется шаг, равный 1. На выходе получаем массив из двух значений 2
и 3. Последний граничный индекс 4 не включается в срез.
• В NumPy срезы возвращают новое представление того же самого
массива, то есть, данные, на которые ссылаются переменные a и b
одни и те же.

38.

Итерирование массивов
• Итерирование двумерных массивов можно выполнять с помощью
вложенных циклов, например:
• for row in x:
• for val in row:
print(val, end=' ')
• print()
• Если же необходимо просто перебрать все элементы многомерного
массива, то можно использовать свойство flat:
• for val in x.flat:
• print(val, end=' ')

39.

Базовые операции над массивами
• Предположим, имеется обычный список и массив, созданный на его
основе:
• lst = [1, 2, 3]
• a = np.array([1, 2, 3])
• Принципиальная разница между двумя этими объектами. Умножим их
на число 2:
• lst*2 # список: [1, 2, 3, 1, 2, 3]
• a*2 # массив: array([2, 4, 6])
• При умножении списка языка Python, он дублируется дважды, а при
умножении на NumPy массив – каждый его элемент умножается
математически на число 2.

40.

базовые математические операции

41.

Примеры операций
• Пусть у нас задан тот же одномерный массив:
• a = np.array([1, 2, 3])
• Все указанные в таблице операции выполняются следующим образом:
• -a # унарный минус
• a + 2 # сложение с числом
• 2 + a # так тоже можно записывать
• a - 3 # вычитание с числом
• a * 5 # умножение на число
• a / 5 # деление на число
• a // 2 # целочисленное деление
• a ** 3 # возведение в степень 3
• a % 2 # вычисление по модулю 2

42.

Примеры операций
• добавим еще один массив:
• b = np.array([3, 4, 5])
• и посмотрим на эти же операции, но с участием двух массивов:
• a - b # array([-2, -2, -2])
• b + a # array([4, 6, 8])
• a * b # array([ 3, 8, 15])
• b / a # array([3. , 2. , 1.66666667])
• b // a # array([3, 2, 1], dtype=int32)
• b ** a # array([ 3, 16, 125], dtype=int32)
• b % a # array([0, 0, 2], dtype=int32)
• Везде мы видим поэлементные операции. Соответственно, чтобы они
выполнялись, массивы должны быть согласованы по длине.

43.

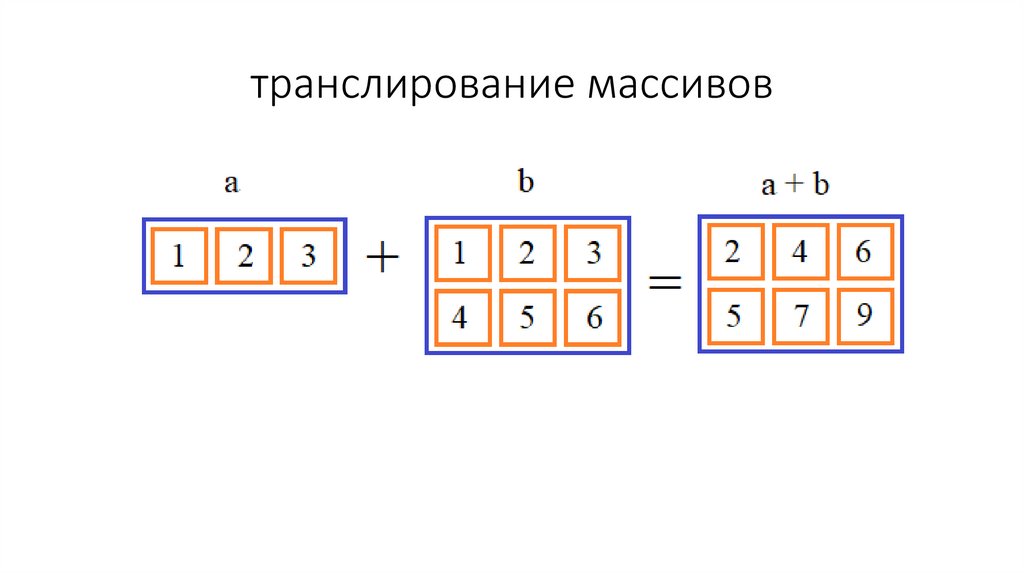
транслирование массивов

44.

Булевы операции
• Предположим, имеется одномерный массив:
• a = np.array([1, 2, 3, 10, 20, 30])
• и мы хотим определить все числа, которые больше 5:
• indx = a > 5
• a[indx]
• На выходе получим массив из трех элементов, которым
соответствуют позиции True:
• array([10, 20, 30])

45.

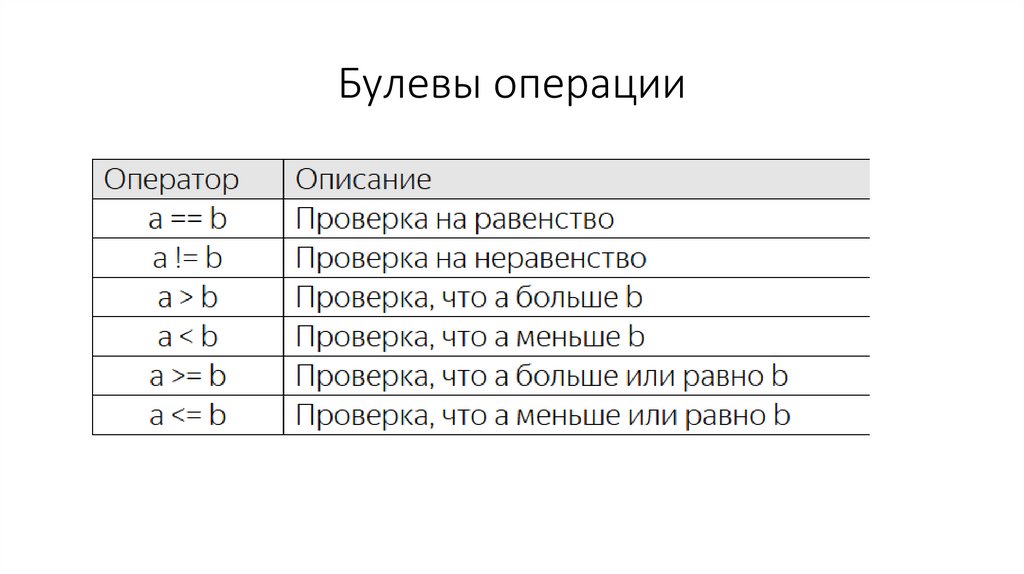
Булевы операции

46.

примеры
• a = np.array([1, 2, 3, 10, 20, 30])
• добавим еще один массив:
• b = np.array([1, 2, 3, 4, 5, 6])
• Тогда можно использовать сравнения:
• a == b # array([ True, True, True, False, False, False])
• a >= b # array([ True, True, True, True, True, True])
• a <= b # array([ True, True, True, False, False, False])
• a != b # array([False, False, False, True, True, True])

47.

np.array_equal
• использовать результат сравнения в условных операторах нельзя.
Следующая строчка приведет к ошибке:
• if(a == b): print("a == b")
• Для такого сравнения массивов необходимо получать только одно
значение True или False, а не объект array. Для этого в пакете NumPy
существуют специальная функция np.array_equal(), которую можно
применить так:
• if np.array_equal(a ,b):
• print("a == b")
• Это условие сработает, если оба массива a и b содержат одинаковые
значения элементов и равны по длине.

48.

Функции all и any
• Если нам нужно определить, что хотя бы один элемент массива
удовлетворяет указанному условию, то можно воспользоваться функцией
any(), например:
• # для массива a = array([ 1, 2, 3, 10, 20, 30])
• np.any(a > 5) # True
• np.any(a == 5) # False
• np.any(a == b) # True
• Если же нужно узнать, все ли элемента массива удовлетворяют условию, то
используется функция all():
• np.all(a > 5)
# False
• np.all(a > 0)
# True
• np.all(a == b) # False

49.

Функции sum, mean, min и max
• Пусть, как всегда, у нас имеется одномерный массив:
• a = np.array([ 1, 2, 3, 10, 20, 30])
• Вычислим сумму, среднее значение и найдем максимальное и
минимальное значения:
• a.sum() # 66
• a.mean() # 11.0
• a.max() # 30
• a.min() # 1

50.

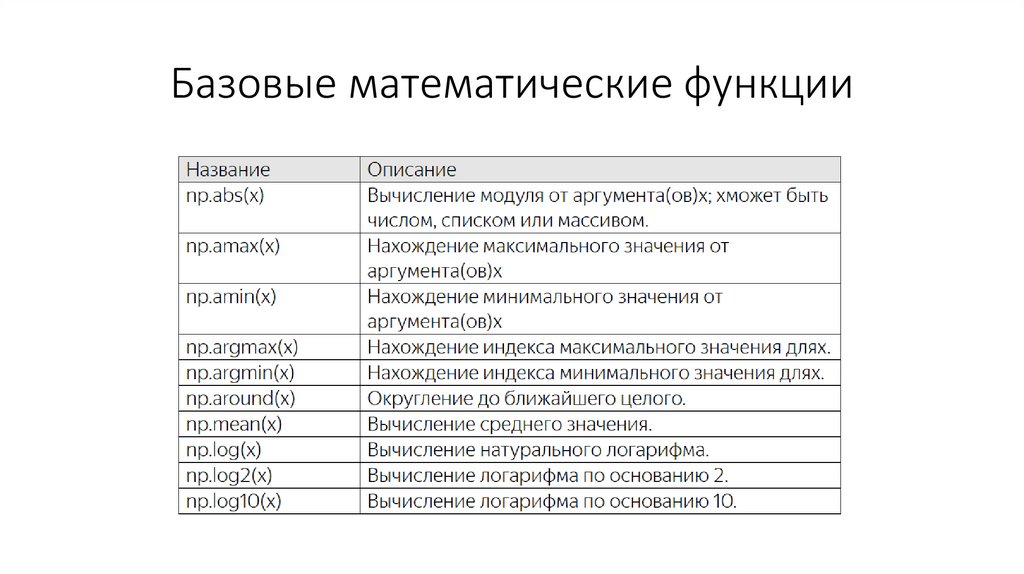
Базовые математические функции

51.

52.

Функции генерации псевдослучайных чисел
• В самом простом случае, функция rand() позволяет получать случайные
числа в диапазоне от 0 до 1:
• np.random.rand() # вещественное случайное число от 0 до 1
• Если требуется получить массив из таких чисел, то можно указать это
через первый аргумент:
• np.random.rand(5) # array([0.78191696, 0.66581136, 0.46458873,
0.76416839, 0.28206656])
• Для получения двумерных массивов – два аргумента:
• np.random.rand(2, 3) # массив 2x3
• И так далее. Можно создавать любые многомерные массивы из
случайных величин.

53.

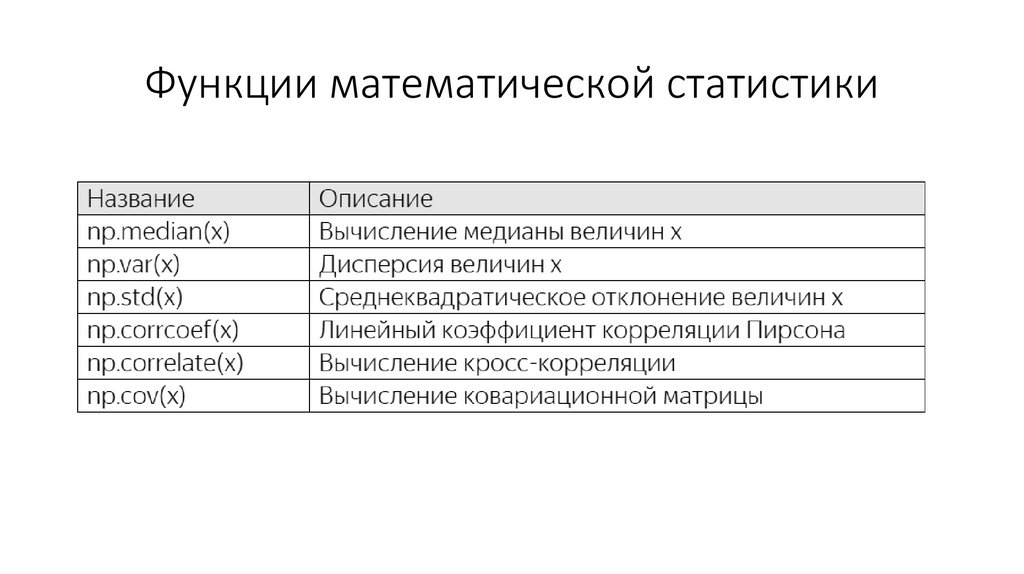
Функции математической статистики

54.

Функции математической статистики
• Предположим, имеются следующие векторы:
• x = np.array([1, 4, 3, 7, 10, 8, 14, 21, 20, 23])
• y = np.array([4, 1, 6, 9, 13, 11, 16, 19, 15, 22])
• Эти числа будем воспринимать как реализации случайных величин X и
Y. Тогда, для вычисления медианы СВ X, можно воспользоваться
функцией:
• np.median(x) # 9.0
• Для расчета дисперсии и СКО, функциями:
• np.var(x) # дисперсия СВ X на основе реализации x
• np.std(y) # СКО СВ Y на основе реализации y

55.

Функции математической статистики
• Далее, чтобы рассчитать коэффициент корреляции Пирсона,
объединим массивы x и y построчно:
• XY = np.vstack([x, y]) # матрица 2x10
• и выполним функцию:
• np.corrcoef(XY)
• Результатом будет матрица 2x2:
• array([[1.
, 0.93158099],
[0.93158099, 1.
]])

56.

Функции математической статистики
• Как ее следует интерпретировать? В действительности, это
автоковариационная матрица вектора СВ[X, Y]
• (В этой формуле полагается, что СВ X и Y центрированы, то есть
имеют нулевое математическое ожидание).

57.

Функции математической статистики
• Если нужно вычислить не нормированное МО, то есть,
автоковариационную матрицу, то следует
воспользоваться функцией:
• np.cov(XY) # ковариационная матрица размерностью
2x2
• Наконец, для вычисления взаимной корреляции между
двумя векторами x и y, используется функция:
• np.correlate(x, y) # array([1736])

58.

Решение СЛАУ
В NumPy решение такой системы можно найти с помощью функции numpy.linalg.solve(a, b), где первый аргумент — матрица A, второй —
столбец b.
a = np.array([[3, 1], [1, 2]])
b = np.array([9, 8])
x = np.linalg.solve(a, b)
print ("Матрица A:\n", a)
print ("Вектор b:\n", b)
print ("Решение системы:\n", x)
Матрица A:
[[3 1]
[1 2]]
Вектор b:
[9 8]
Решение системы:
[2. 3.]
Убедимся, что вектор x действительно является решением системы:
print (a.dot(x))
[9. 8.]

59.

В NumPy обратные матрицы вычисляются с помощью
функции numpy.linalg.inv(a), где a — исходная матрица
a = np.array([[1, 2, 1], [1, 1, 4], [2, 3, 6]], dtype=np.float32)
b = np.linalg.inv(a)
print ("Матрица A:\n", a)
print ("Обратная матрица к A:\n", b)
print ("Произведение A на обратную должна быть единичной:\n", a.dot(b))
Матрица A:
[[1. 2. 1.]
[1. 1. 4.]
[2. 3. 6.]]
Обратная матрица к A:
[[ 6. 9. -7.]
[-2. -4. 3.]
[-1. -1. 1.]]
Произведение A на обратную должна быть единичной:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]

60.

Произведение матриц
• В NumPy произведение матриц вычисляется с помощью функции
numpy.dot(a, b, ...) или с помощью метода array1.dot(array2), где array1
и array2 — перемножаемые матрицы.
• a = np.array([[1, 0], [0, 1]])
• b = np.array([[4, 1], [2, 2]])
• r1 = np.dot(a, b)
• r2 = a.dot(b)
• print ("Матрица A:\n", a)
• print ("Матрица B:\n", b)
• print ("Результат умножения функцией:\n", r1)
• print ("Результат умножения методом:\n", r2)