Многогранники как объекты интерьера в школьном помещении. Проектно-изыскательская работа

1.

Муниципальное автономное общеобразовательное учреждение города Кургана «Гимназия №30»
ПРОЕКТНО – ИЗЫСКАТЕЛЬСКАЯ РАБОТА
Многогранники как объекты интерьера в школьном помещении
Автор: Иванов Никита Денисович
МАОУ «Гимназия №30»
6 А класс
Руководитель: Лисихина Ольга Александровна
Учитель математики
МАОУ «Гимназия №30»
Курган
2023 г

2.

На данный момент времени я уже имею представление о таких многогранниках как куб,
призма, прямоугольный параллелепипед и пирамида. Яркими примерами многогранников,
которые я могу назвать, это - древние Египетские пирамиды, объекты дизайна, природные
кристаллы, упаковка. Ну вот пожалуй и все.
У меня возникают вопросы:
Почему мы изучаем многогранники каждый год в школе?
Почему к ним обращались великие ученные Пифагор, Евклид, Архимед, Леонардо да Винчи?
Что в многогранниках особенного и зачем они нужны нам сейчас в современном мире?

3.

Цель: изучить многогранники Платона и Архимеда. Выполнить макет
«Математическая площадка в здании школы» с помощью моделей
многогранников.
Задачи:
- познакомится с понятием «многогранник», и рассмотреть какие бывают
многогранники;
- найти примеры в истории и нашей современной жизни, где встречаются и
используются модели многогранников;
- найти информацию о «макетах», о том, как они выполняются;
- изучить способы выполнения моделей многогранников из бумаги;
- выполнить бумажные модели многогранников;
- рассчитать и выполнить макет с использованием моделей многогранников
из бумаги.

4.

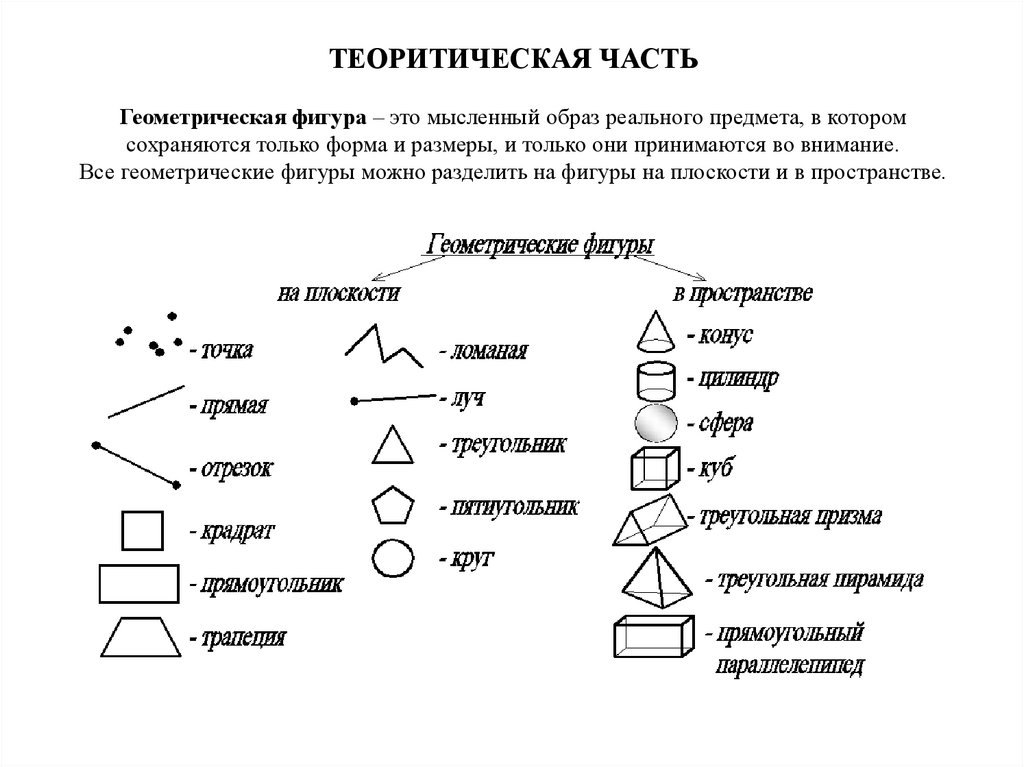
ТЕОРИТИЧЕСКАЯ ЧАСТЬ
Геометрическая фигура – это мысленный образ реального предмета, в котором
сохраняются только форма и размеры, и только они принимаются во внимание.
Все геометрические фигуры можно разделить на фигуры на плоскости и в пространстве.

5.

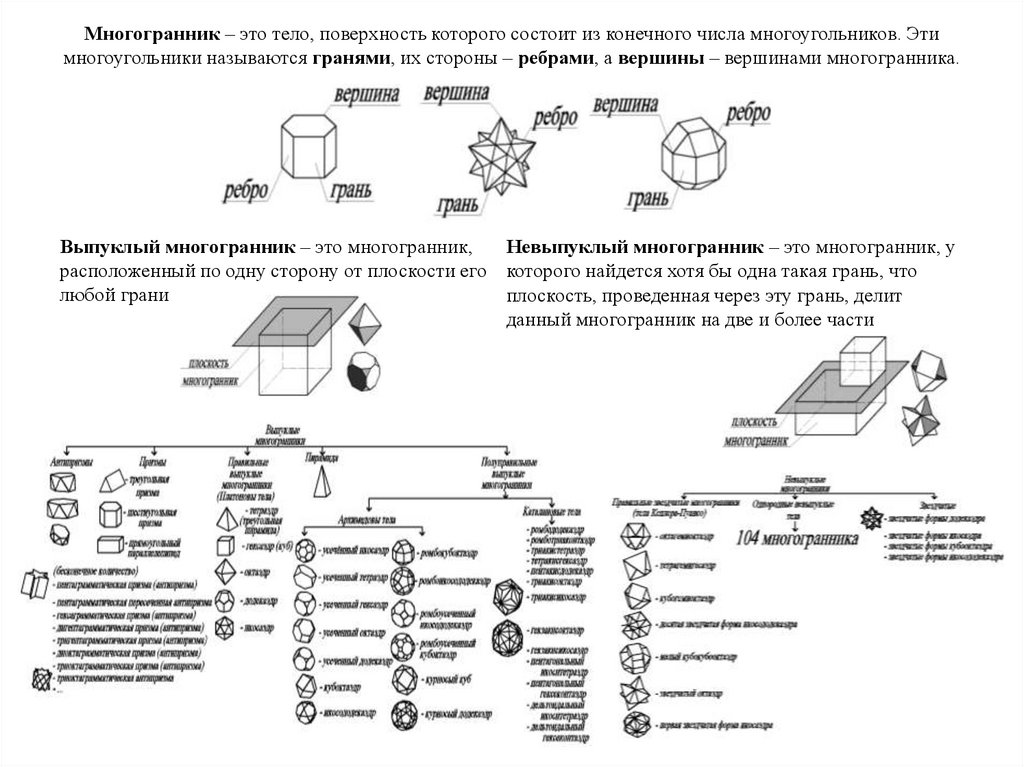
Многогранник – это тело, поверхность которого состоит из конечного числа многоугольников. Эти
многоугольники называются гранями, их стороны – ребрами, а вершины – вершинами многогранника.
Выпуклый многогранник – это многогранник,
Невыпуклый многогранник – это многогранник, у
расположенный по одну сторону от плоскости его которого найдется хотя бы одна такая грань, что
любой грани
плоскость, проведенная через эту грань, делит
данный многогранник на две и более части

6.

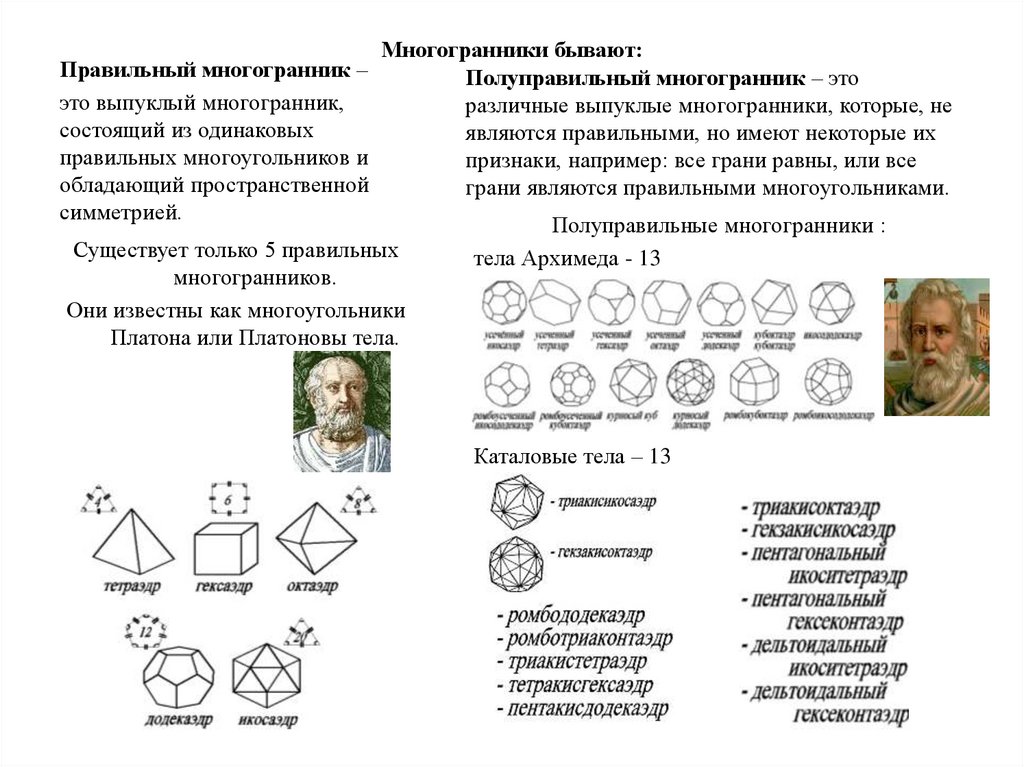
Правильный многогранник –
это выпуклый многогранник,
состоящий из одинаковых
правильных многоугольников и
обладающий пространственной
симметрией.
Многогранники бывают:
Полуправильный многогранник – это
различные выпуклые многогранники, которые, не
являются правильными, но имеют некоторые их
признаки, например: все грани равны, или все
грани являются правильными многоугольниками.
Существует только 5 правильных
многогранников.
Они известны как многоугольники
Платона или Платоновы тела.
Полуправильные многогранники :
тела Архимеда - 13
Каталовые тела – 13

7.

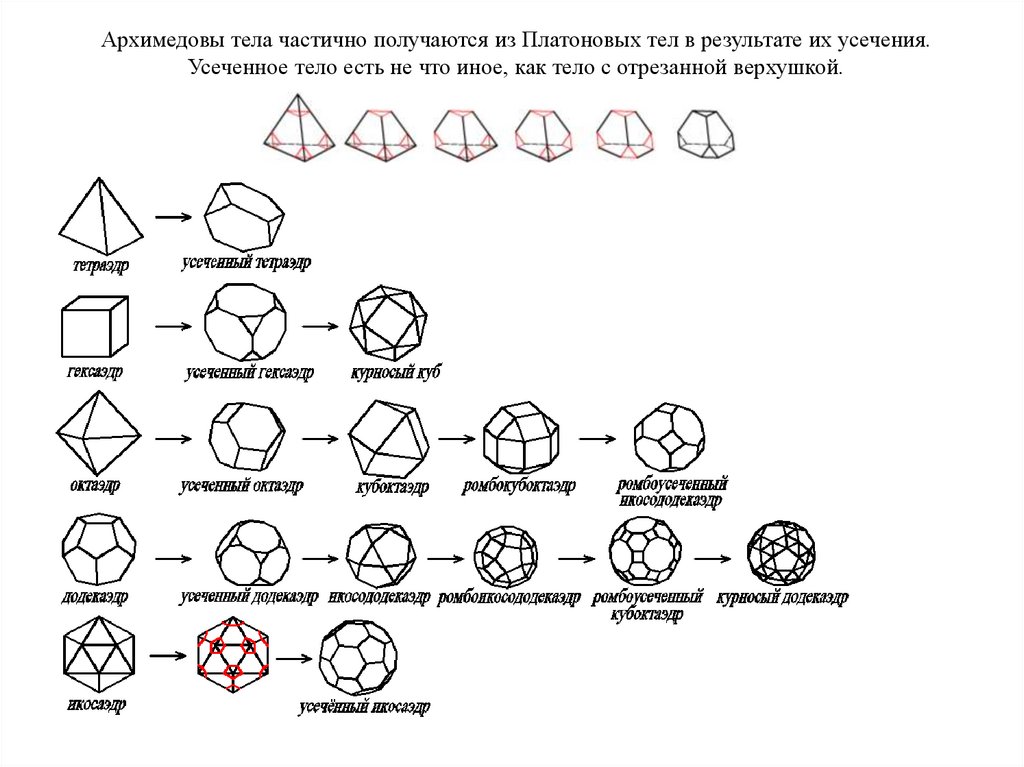
Архимедовы тела частично получаются из Платоновых тел в результате их усечения.
Усеченное тело есть не что иное, как тело с отрезанной верхушкой.

8.

Сферы жизни человечества, где присутствуют многогранники
В природе: структура ДНК, кристаллы, феодарий, пчелиные соты. Земля. Вселенная.
В науке, искусстве, архитектуре и искусстве, городской среде, машиностроении,
робототехнике, дизайне, играх

9.

Макет – модель, предварительный образец, пробный образец чего-либо.
Перед выполнением макета может выполняться ряд эскизов, чертежей, как на бумаге, так
и на компьютере. Макеты выполняются из разнообразных материалов – дерева, картона,
бумаги, пластмассы, с использованием уже готовых элементов и изделий, природных
материалов. Для придания макетам выразительности используют лазерную резку, печать на
3D-принтерах, фотопечать, светодиодную подсветку.
Макеты выполняются в трехмерном пространстве, в масштабе
Трехмерное пространство – это
геометрическая модель материального
мира, в котором мы находимся. Здесь три
однородных измерения – длина, ширина
и высота
Масштаб — отношение двух линейных размеров.
В математике масштаб определяется как
отношение расстояния на карте к
соответствующему расстоянию на реальной
местности. Во многих областях практического
применения масштабом называют отношение
размера изображения к размеру изображаемого
объекта.

10.

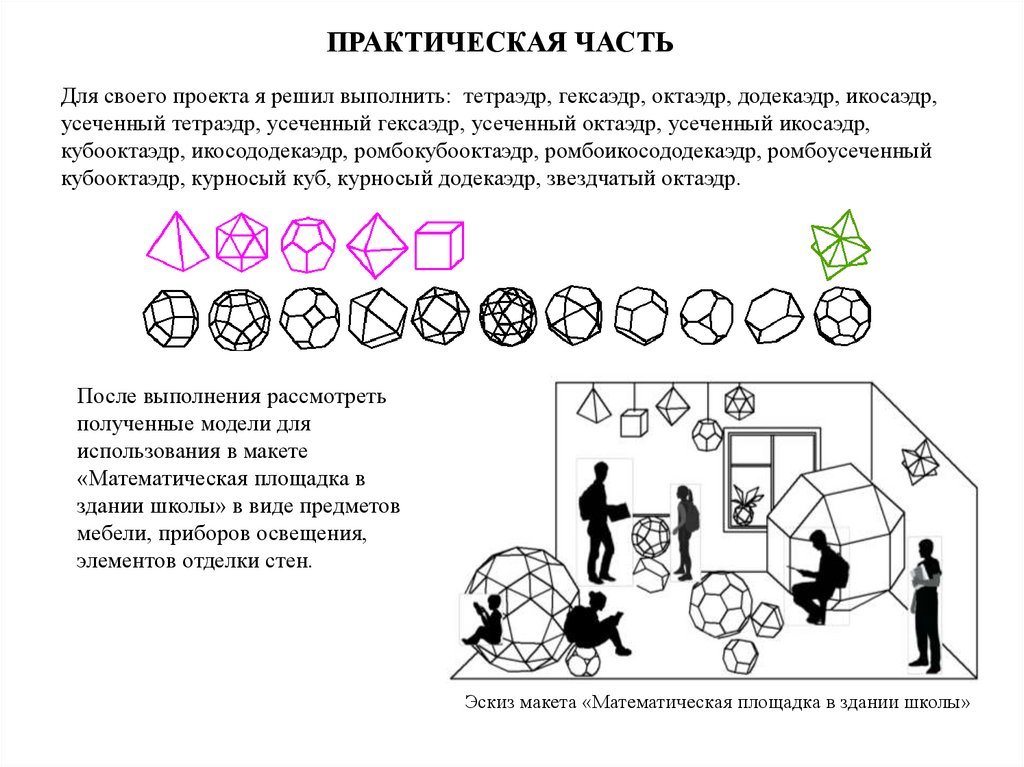
ПРАКТИЧЕСКАЯ ЧАСТЬ
Для своего проекта я решил выполнить: тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр,
усеченный тетраэдр, усеченный гексаэдр, усеченный октаэдр, усеченный икосаэдр,
кубооктаэдр, икосододекаэдр, ромбокубооктаэдр, ромбоикосододекаэдр, ромбоусеченный
кубооктаэдр, курносый куб, курносый додекаэдр, звездчатый октаэдр.
После выполнения рассмотреть
полученные модели для
использования в макете
«Математическая площадка в
здании школы» в виде предметов
мебели, приборов освещения,
элементов отделки стен.
Эскиз макета «Математическая площадка в здании школы»

11.

Выполнение моделей многогранников из бумаги
Выбор размеров моделей многогранников
Задавать размеры будущим моделям многогранников можно двумя вариантами:
- вариант №1: создать модели,
вписанные в сферу заданных размеров
- вариант №2: задать единую длину стороны
для всех многоугольников, из которых будет собрана
модель (мой вариант)
При рассмотрении фото для варианта №2 на этом слайде получается, что самыми маленькими
моделями будут тетраэдр и гексаэдр, более сложные модели будут по высоте превышать в 4-5 раз.
Поэтому, чтобы макет не получился больших размеров и при учете удобства склеивания моделей
из бумаги, я предположу, что единый размер ребра равный 3см будет оптимальным вариантом.
Для удобства выполнения моделей, рационально использовать шаблоны многоугольников,
которые я сделаю из плотного картона.
Шаблон – это образец, по которому изготовляются какие-нибудь одинаковые изделия.

12.

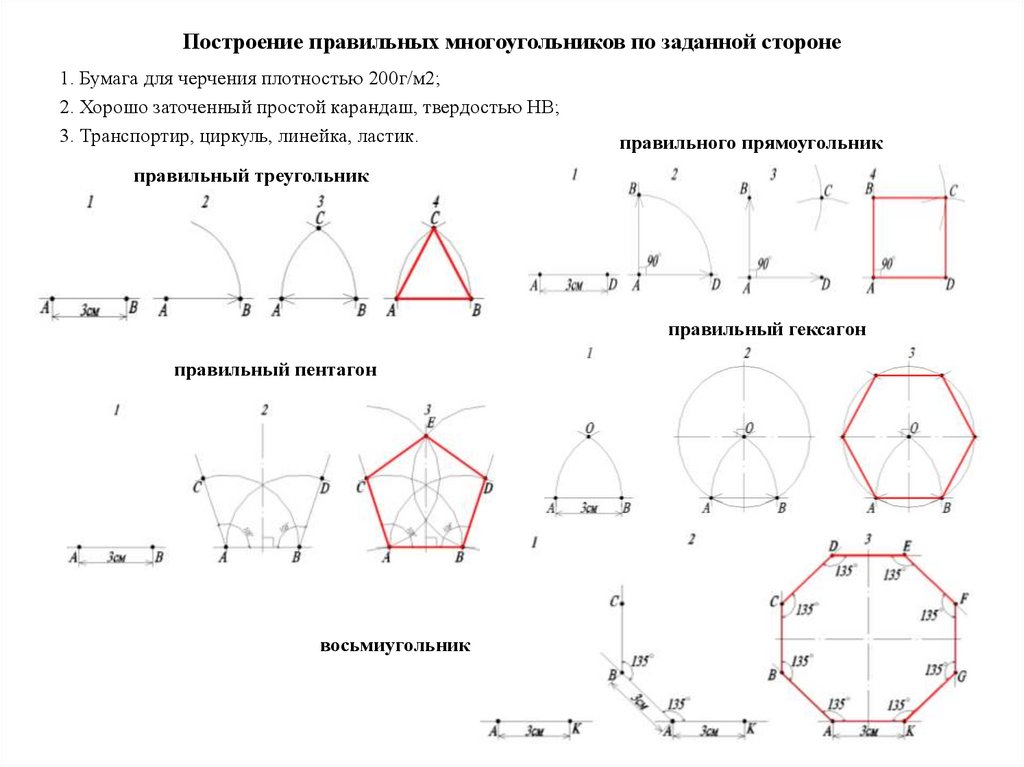
Построение правильных многоугольников по заданной стороне
1. Бумага для черчения плотностью 200г/м2;
2. Хорошо заточенный простой карандаш, твердостью НВ;
3. Транспортир, циркуль, линейка, ластик.
правильного прямоугольник
правильный треугольник
правильный гексагон
правильный пентагон
восьмиугольник

13.

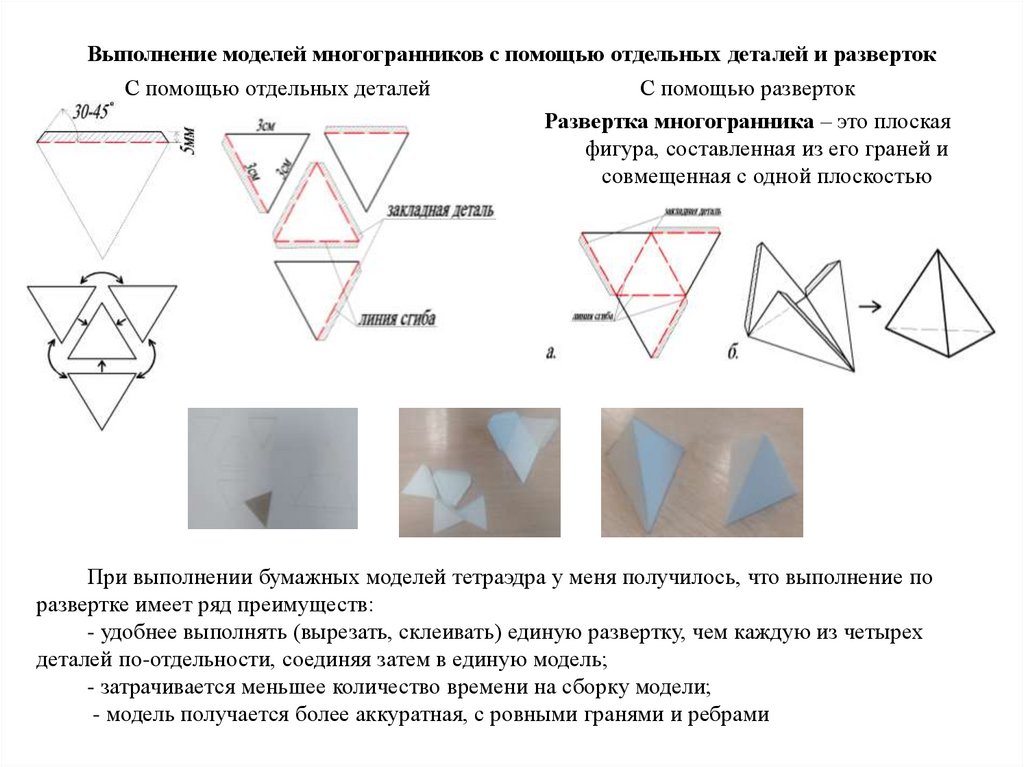
Выполнение моделей многогранников с помощью отдельных деталей и разверток
С помощью отдельных деталей
С помощью разверток
Развертка многогранника – это плоская
фигура, составленная из его граней и
совмещенная с одной плоскостью
При выполнении бумажных моделей тетраэдра у меня получилось, что выполнение по
развертке имеет ряд преимуществ:
- удобнее выполнять (вырезать, склеивать) единую развертку, чем каждую из четырех
деталей по-отдельности, соединяя затем в единую модель;
- затрачивается меньшее количество времени на сборку модели;
- модель получается более аккуратная, с ровными гранями и ребрами

14.

Готовые модели многогранников, сделанные с помощью разверток, для моего проекта

15.

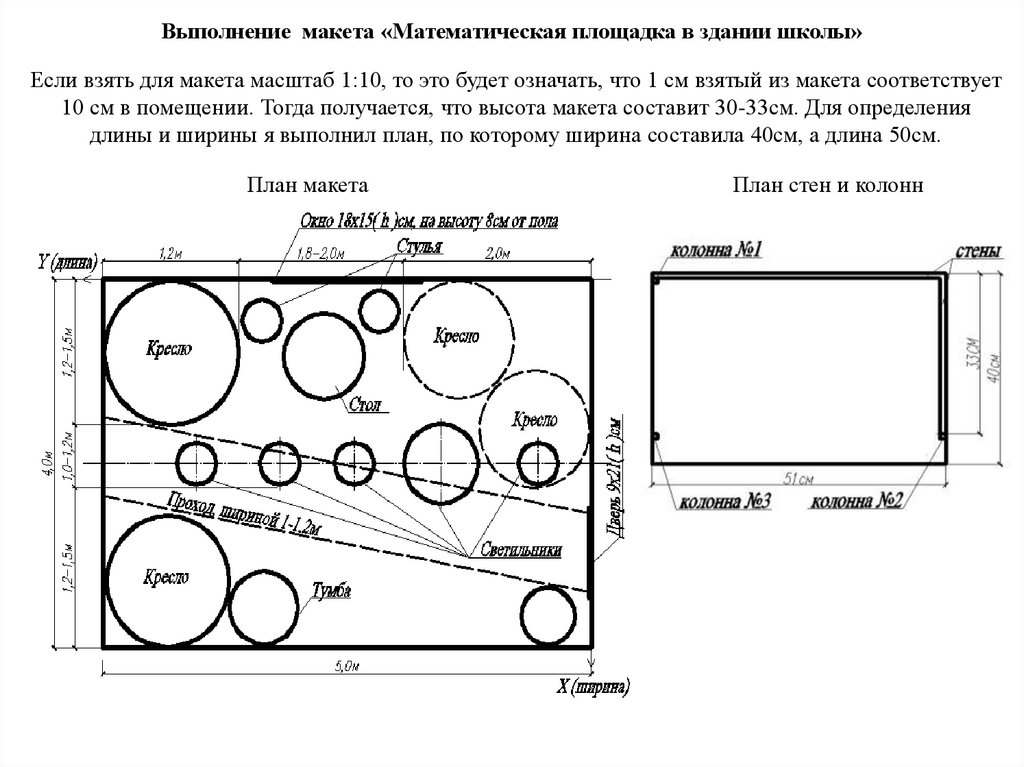
Выполнение макета «Математическая площадка в здании школы»
Если взять для макета масштаб 1:10, то это будет означать, что 1 см взятый из макета соответствует
10 см в помещении. Тогда получается, что высота макета составит 30-33см. Для определения
длины и ширины я выполнил план, по которому ширина составила 40см, а длина 50см.
План макета
План стен и колонн

16.

Выполнение основания макета
1. Лист фанеры толщиной 5мм, размером 34х51см;
2. бумага для черчения (плотностью 200г/м2) формат А1 – 2 листа;
3. двухсторонний скотч (шириной 1см, желательно белого цвета), бумажный скотч шириной 2 и 4см, клей ПВА;
4. деревянные стержни (d5мм, длиной 40см) – 3штуки;
5. простой твердый карандаш, линейка, ножик для резки пластилина, ножницы, прозрачный скотч шириной 1см;
6. иголка и белые нитки.

17.

Выполнения элементов интерьера из моделей многогранников
1. готовые многогранники;
2. простой твердый карандаш, линейка, ножницы;
3. клей ПВА;
4. небольшой канцелярский скальпель для подрезки;
5. цветная гуашь (12 цветов), кисти синтетические округлой формы (№2) и плоской (№4 и №8).
№п/п
Наименование
№п/п
Наименование
1
тетраэдр - светильник
10
кубооктаэдр - табурет
2
гексаэдр - светильник
11
икосододекаэдр - стол
3
октаэдр - светильник
12
ромбокубооктаэдр полка
4
додекаэдр- светильник
13
ромбоикосододекаэдр кресло
5
икосаэдр - светильник
14
ромбоусеченный
кубооктаэдр - кресло
6
усеченный тетраэдр -
15
курносый куб - вазон
16
курносый додекаэдр -
табурет
7
усеченный октаэдр стол
8
усеченный куб - полка
кресло
17
звездчатый октаэдрсветильник
9
усеченный икосаэдр кресло

18.

Макет ««Математическая площадка в здании школы»

19.

Выводы
Вывод по теоретической части
Человечество с Древних времен изучала объемные фигуры – многогранники. И
сегодня я вижу результат их изучения – это познание природы, создание техники,
преобразование мира. Многогранники повсюду в нашей жизни, они пронизывают
все сферы человечества. Они из века в век оказывают влияние на людей науки,
изобретателей, архитекторов, художников, музыкантов подталкивая на создание
шедевров. Они настолько сильно вошли в практическую жизнь человека –
строительство зданий и сооружений, машиностроение, создание приборов
различного назначение, спорт, медицина, дизайн, что мы даже не замечаем их.
Сегодня известно и изучено большое количество многогранников. Это
многогранники Платона, Архимеда, Каталоновы тела, красивейшие звездчатые виды
многогранников. Я считаю, что впереди еще множество открытий, но самое
интересное - это нахождение решений, где и как новаторски можно
будет применить формы и свойства многогранников.

20.

Вывод по практической части
Выводы по выполнению бумажных моделей многогранников
- я научился строить 3,4,5,6 и 8-угольники по заданной стороне;
- я выполнил такие модели как 5 многогранников Платона, 11 многогранников Архимеда, звездчатый
октаэдр;
- я доказал, что бумажные модели многогранников лучше выполнять по единым разверткам, чем из
отдельных многоугольников;
- красота бумажной модели многогранника зависит от правильности построения чертежа деталей и
развертки. Здесь я бы хотел научиться пользоваться линейкой с рейсшиной;
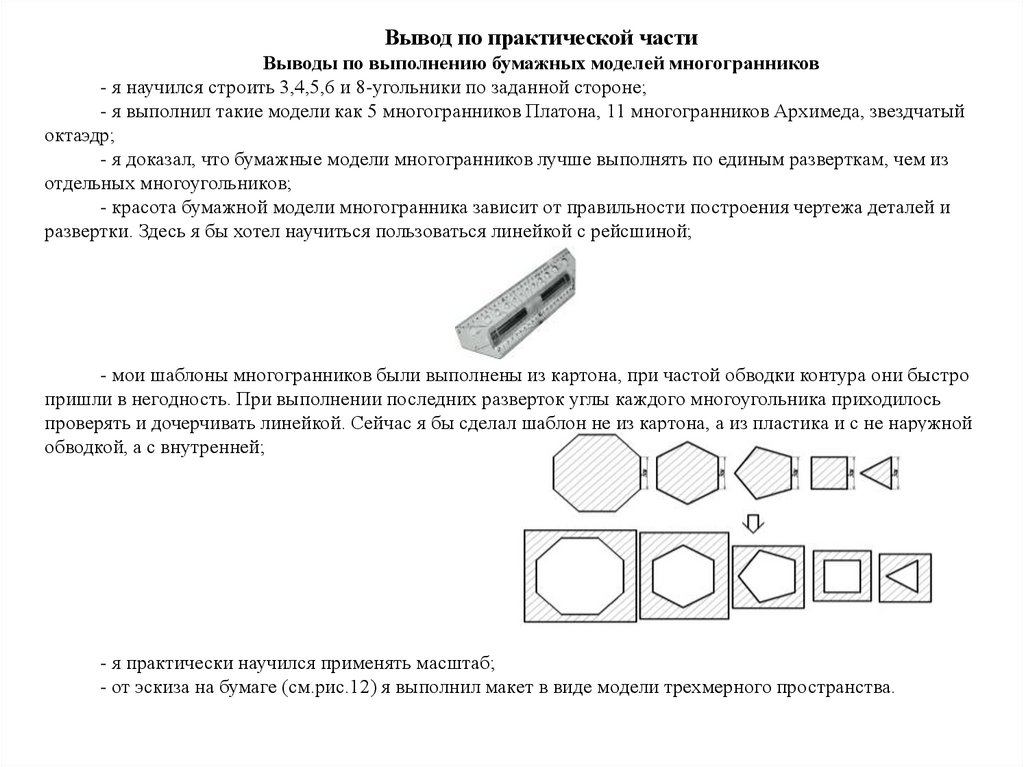
- мои шаблоны многогранников были выполнены из картона, при частой обводки контура они быстро
пришли в негодность. При выполнении последних разверток углы каждого многоугольника приходилось
проверять и дочерчивать линейкой. Сейчас я бы сделал шаблон не из картона, а из пластика и с не наружной
обводкой, а с внутренней;
- я практически научился применять масштаб;
- от эскиза на бумаге (см.рис.12) я выполнил макет в виде модели трехмерного пространства.

21.

Выводы по выполнению макета «Математическая площадка в здании школы»:
- в ходе выполнения работы мне пришлось немного отступить от первоначального эскиза, это
произошло по причине того, что макет – это не простая модель собранная воедино. Он требует точных
расчетов, проработки всех деталей;
- для меня было очень занимательно из готовых бумажных моделей многогранников изобретать
предметов мебели, приборы освещения, собирать их как мозайку в единое целое;
- идею макета можно использовать в таких школьных помещениях, как часть коридора, холла, зала,
светового кармана;
- макет наглядно показывает, как преобразовалось школьное помещение в необычную и
притягательную площадку для учащихся, где можно провести время на перемене или интересное
школьное мероприятие, а также развить свое пространственное мышление, получить дополнительную
информацию про многогранники, их строение, внешний вид, увидеть их вокруг себя в обычной жизни;
- при выполнении проекта я дополнительно выполнил несколько моделей многогранников, которые
использовал при участии в другом школьном конкурсе, где занял призовое место;
- если я дальше решу развивать данный проект, то хотел бы выполнить макет и более сложные
модели многогранников с помощью электронно-вычислительных программ. Подумать над использованием
многогранников в других областях, например в робототехнике.
Думаю, что мой проект оказался для вас интересным и познавательным. После него вы обретете
способность повсюду замечать эти великолепные фигуры.