Решение типовых задач алгебры и анализа

1. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ АЛГЕБРЫ И АНАЛИЗА

2. Цель

• Ознакомиться с основными
операторами для решения задач
алгебры и анализа
2

3. Средства Matlab

Изначально Matlab имел средства только для
численного анализа
Сегодня в Matlab встроены средства
аналитических (символьных) вычислений
– Symbolic Math Toolbox
– Является вычислительным ядром системы Maple V
– Установка Maple не требуется
Символьные вычисления — это преобразования и
работа с математическими равенствами и
формулами, как с последовательностью символов.
3

4. Создание символьных переменных

Для символьного анализа требуется создать символьные
переменные и функции
Символьные переменные создаются
–
по одной: x=sym(’x’)
–
так же можно создать целое символьное выражение
несколько сразу: syms x y z
Символьные функции определяются через символьные
переменные: f=x^2+y
Для построения символьных функций можно
воспользоваться командой ezplot
Представить в стандартной форме – командой pretty
4

5. Символьные вычисления

Преобразования анализа
– дифференцирование, пределы, интегрирование,
разложение в ряд Тейлора
Упрощение и подстановки
Точная арифметика
Линейная алгебра
Решение уравнений и их систем
– обычных и дифференциальных
5

6.

Для проведения аналитических (символьных)
операций нужно, чтобы соответствующие
переменные были предварительно объявлены.
6

7. Упрощение выражений

7

8. Раскрытие скобок

8

9. Вычисление интегралов

а) вычисление неопределенных
интегралов
Для нахождения неопределенных
интегралов в символьном виде
используется функция int, имеющая
следующий синтаксис:
Int(f,x),
где f – подынтегральная функция;
х – переменная интегрирования.
9

10.

Примеры. Вычислить неопределенный
интеграл
10

11. Вычисление определенных интегралов

Для вычисления определенных
интегралов в символьном виде
используется функция int, имеющая
следующий синтаксис:
Int(f,x,a,b),
где f – подынтегральная функция;
х – переменная интегрирования;
a – нижний предел интегрирования;
b – верхний предел интегрирования. 11

12.

Примеры: Вычислить определенный
интеграл
12

13. Вычисление двойных интегралов

13

14. Вычисление тройных интегралов

14

15. Методы приближенного вычисления интегралов

15

16.

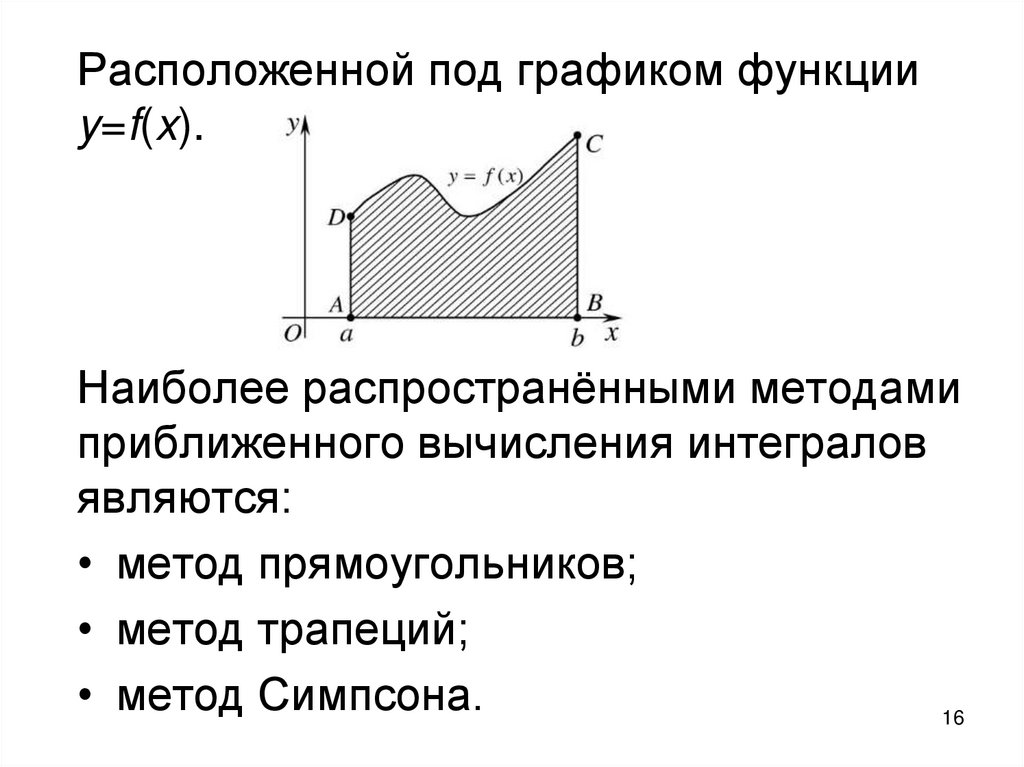
Расположенной под графиком функции
y=f(x).
Наиболее распространёнными методами
приближенного вычисления интегралов
являются:
• метод прямоугольников;
• метод трапеций;
• метод Симпсона.
16

17. Решение уравнений

Для решения алгебраических и
трансцендентных уравнений используется
функция solve(e1,e2,…,en),
здесь
е1, е2, …, еn –символьные выражения
или переменные.
17

18.

Примеры
• Единственное решение
Решить уравнение x+2=0.
18

19.

19

20.

• Уравнение с комплексными корнями
20

21. Решение систем линейных алгебраических уравнений

Для решения систем линейных
алгебраических уравнений используется
знак \ (деление слева).
Например, если требуется решить
систему линейных уравнений Ах=b,
где А – квадратная матрица размера
nxn;
b – заданный вектор-столбец
размера n,
21

22.

то для нахождения неизвестного векторастолбца х достаточно вычислить
выражение A\b.
• Деление слева (\)
– для квадратных матриц
реализует метод Гаусса;
– для прямоугольных матриц–
метод наименьших
квадратов.
22

23.

Функция solve() позволяет решить
систему уравнений. Например, для
системы уравнений вида
>> [x y] = solve('2*x+y=3', '3*x-5*y=11', x, y)
x=2
y = -1
23

24. Символьное решение дифференциальных уравнений

Для решения дифференциальных
уравнений в символьном виде
применяется функция
dsolve(‘строка_символов’) .
Пример.

25.

Символ D в строке уравнения
обозначает дифференцирование по
независимой переменной
25

26.

26

27.

27

28. Вычисление пределов

28

29.

29

30. Вычисление производных

Для вычисления производных в
символьной форме можно использовать
функцию diff( ). Данная функция имеет
несколько форматов вызова. Самый
простой – вычисление производной
символьного выражения, в состав которого
входит одна символьная переменная.
30

31.

31

32.

32

33. Если вторым аргументом указана переменная, то производная будет вычислена по заданной переменной.

33

34.

Функция diff() может получать три аргумента:
первый – дифференцируемое символьное
выражение, второй – переменная
дифференцирования, третий – порядок
дифференцирования.
34