Комбинаторное правило умножения

1.

11.03.2025
Комбинаторное правило умножения.
Статистика – это наука, изучающая
процессы, происходящие в обществе,
оценивающая их количественные и
качественные параметры.
Вероя́тность — степень возможности
наступления некоторого события.
8 класс Вероятность и статистика
Урок 22

2.

Повторение. Подготовка к ВПР
9. В случайном эксперименте бросают две игральные
кости. Найдите вероятность того, что числа выпавших
очков будут отличаться друг от друга на 1 или на 2.
10. Оля нарисовала схему, не отрывая
карандаша от листа бумаги и не проводя
никакую линию дважды. В какой точке
Оля закончила рисовать схему, если она
начала её рисовать в точке E?

3.

выполнить:
1. Сколько существует двузначных чисел?
Сколько из них чётных?
Сколько кратных 5?
2. Сколько двузначных чисел можно записать
цифрами:
а) 0 и 5; б) 1 и 5; в) 0, 1 и 5?

4.

Комбинаторное
правило умножения

5.

Слово «комбинаторика» происходит от
латинского слова combinare, которое означает
«соединять, сочетать».
Комбинаторика – это раздел математики,
занимающийся решением комбинаторных задач.
Комбинаторная задача – задача, для решения
которой необходимо составлять различные
комбинации из конечного числа элементов и
подсчитывать число комбинаций.

6.

ИСТОРИЧЕСКАЯ СПРАВКА
Термин "комбинаторика" был
введён в математический обиход
всемирно
известным
немецким
учёным Г.В.Лейбницем, который в
1666 году опубликовал "Рассуждения
о комбинаторном искусстве".
Немецкий философ и математик
Готфрид фон Лейбниц
Комбинаторика – это раздел математики, в
котором изучаются различных вопросы о том,
сколько комбинаций, подчиненных тем или
иным условиям, можно составить из заданных
объектов.

7.

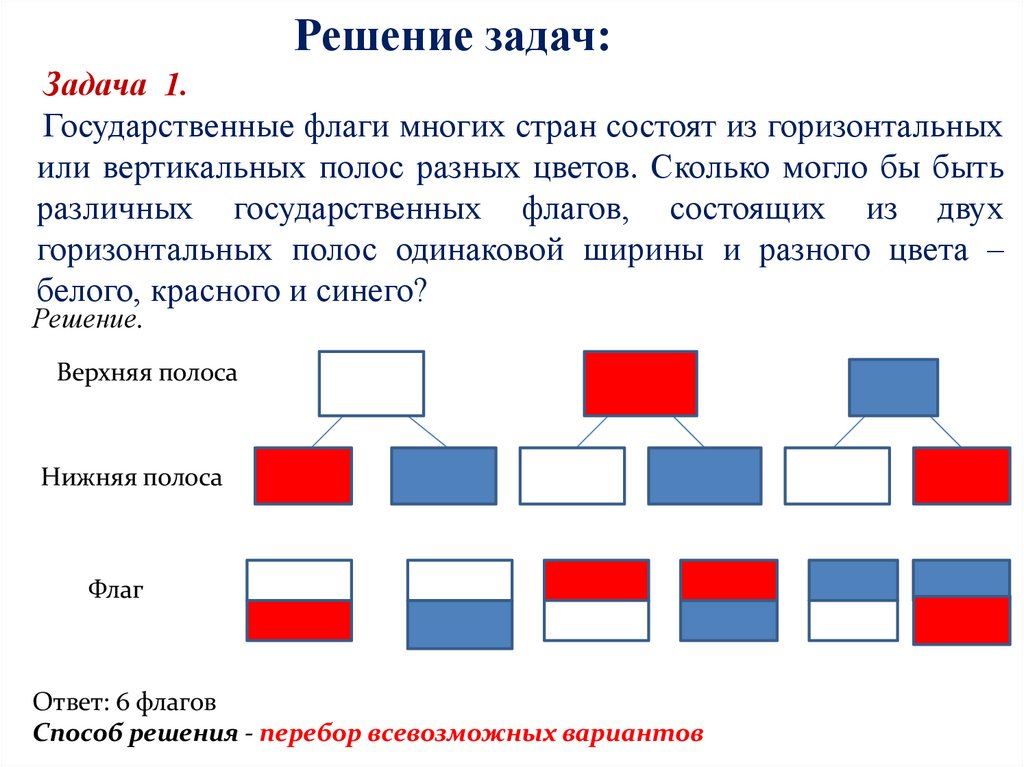
Решение задач:
Задача 1.
Государственные флаги многих стран состоят из горизонтальных
или вертикальных полос разных цветов. Сколько могло бы быть
различных государственных флагов, состоящих из двух
горизонтальных полос одинаковой ширины и разного цвета –
белого, красного и синего?
Решение.
Верхняя полоса
Нижняя полоса
Флаг
Ответ: 6 флагов
Способ решения - перебор всевозможных вариантов

8.

Задача 2.
Из цифр 1, 2, 3, 4 необходимо составить шифр в виде
трёхзначного числа так, чтобы каждая цифра встречалась только
один раз. Сколькими способами можно составить такой шифр?
Решение.
1
2
3 4
3
2
4
1
3
4
3
4
1
2
4
2 4 23 3 4141 3 4 24 12 1
1
2
3
2 3 1 3 1 2
123, 124, 132, 134, 142, 143, 213, 214, 231, 234, 241, 243, 312,
314, 321, 324, 341, 342, 412, 413, 421, 423, 431, 432.
Полученная схема - дерево возможных вариантов или древо
графов

9.

Второй способ решения.
Первую цифру можно выбрать четырьмя способами. Так как
после выбора первой цифры останутся три, то вторую цифру
можно выбрать уже тремя способами. Наконец, третью цифру
можно выбрать (из оставшихся двух) двумя способами.
Следовательно, общее число искомых трехзначных чисел равно
произведению
4 • 3 • 2 = 24
комбинаторное правило умножения
Пусть имеется п элементов и требуется выбрать из них
один за другим k элементов. Если первый элемент можно
выбрать п1 способами, после чего второй элемент можно
выбрать п2 способами из оставшихся, затем третий
элемент можно выбрать п3 способами из оставшихся и т. д.,
то число способов, которыми могут быть выбраны все k
элементов, равно произведению п1 • п2 • п3 • ... • nk.

10.

Задача 3.
В 9 классе 20 человек. Необходимо выбрать 2 представителя от
класса в совет школы. Сколькими способами это можно сделать?
Решение.
Воспользуемся комбинаторным правилом умножения, получим
20 ∙ 19 = 380
Ответ: 380

11.

Задача 4.
Из цифр 2, 4, 7 следует составить трехзначное число. Сколько
всего таких чисел можно составить?
Решение:
1 способ.
Найдём количество чисел, которые начинаются цифрой 2:
247, 274, 244, 277, 222, 242, 272, 227, 224 – 9 чисел;
Найдём количество чисел, которые начинаются цифрой 4:
447, 474, 444, 477, 422, 442, 472, 427, 424 – 9 чисел;
Найдём количество чисел, которые начинаются цифрой 7:
747, 774, 744, 777, 722, 742, 772, 727, 724 – 9 чисел;
Всего: 9+9+9 = 27 чисел

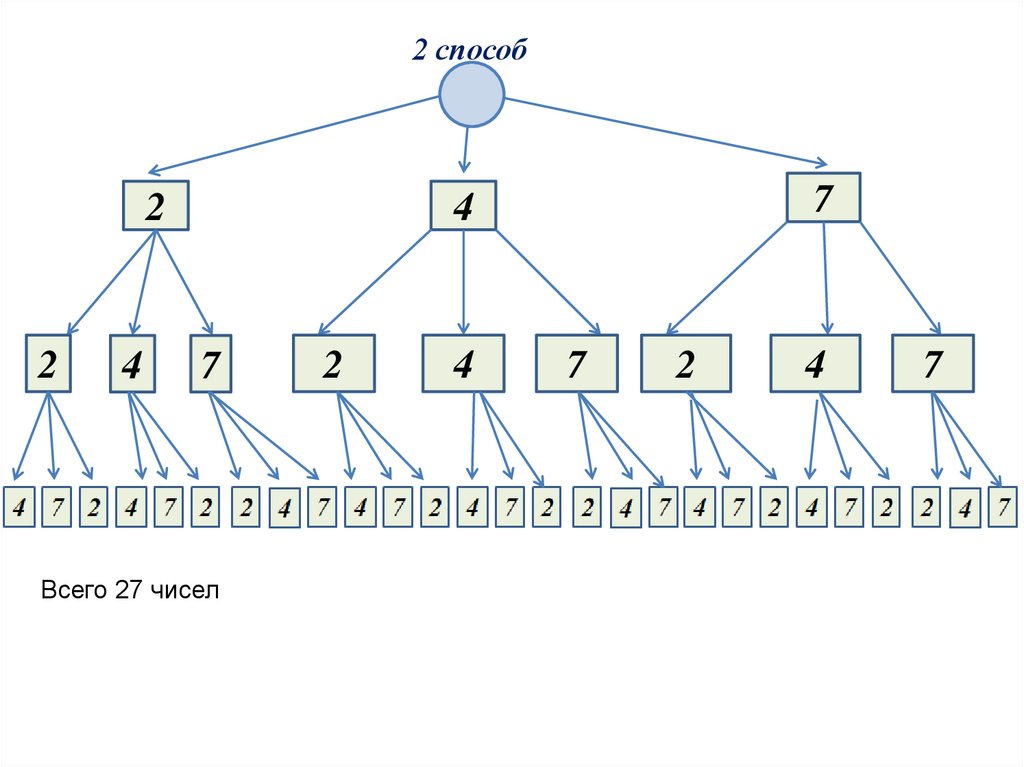
12. 2 способ

2
2
4
7
4
7
Всего 27 чисел
2
4
7
2
4
7

13. Комбинаторное правило умножения

Если элемент А можно выбрать m способами, а
другой объект В можно выбрать k способами, то
объект А и В можно выбрать