Комбинаторное правило умножения

1.

Комбинаторное
правило умножения

2.

Задача № 1. Из цифр 2, 4, 7 следует составить трехзначное
число. Сколько всего таких чисел можно составить?
Решение:
1 способ
Найдём количество чисел, которые начинаются цифрой 2: 247, 274, 244,
277, 222, 242, 272, 227, 224 – 9 чисел;
Найдём количество чисел, которые начинаются цифрой 4: 447, 474, 444,
477, 422, 442, 472, 427, 424 – 9 чисел;
Найдём количество чисел, которые начинаются цифрой 7: 747, 774, 744,
777, 722, 742, 772, 727, 724 – 9 чисел;
Всего: 9+9+9 = 27 чисел

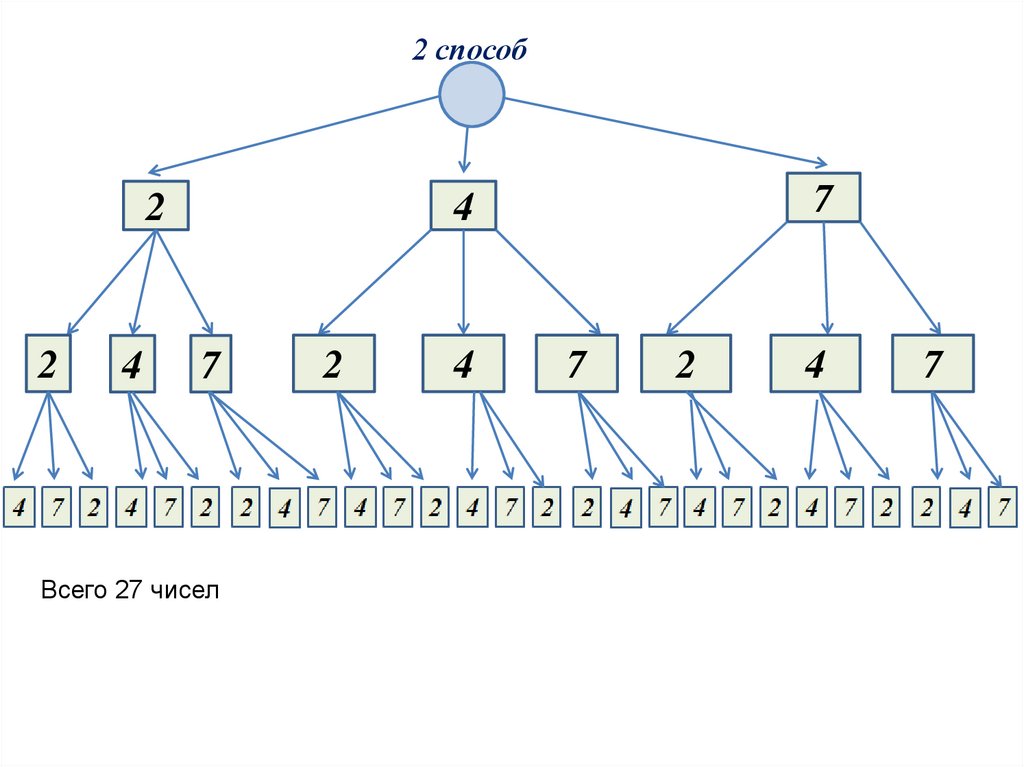
3. 2 способ

2
2
4
7
4
7
Всего 27 чисел
2
4
7
2
4
7

4. Комбинаторное правило умножения

Если элемент А можно выбрать m способами, а
другой объект В можно выбрать k способами, то
объект А и В можно выбрать