Радиотехнические сигналы БРЭО

1.

Лекция 3 Радиотехнические сигналы БРЭО
Рассматриваемые вопросы:
Анализ
свойств
радиотехнических
сигналов,
применяемых
в
бортовом
радиоэлектронном оборудовании воздушных судов. Частотные характеристики
амплитудно-модулированных сигналов, радиотехнических сигналов с угловой модуляцией, с
импульсной модуляцией, манипулированных радиотехнических сигналов.
1

2.

Сигналы, поступающие из источника сообщений (микрофона, передающая телевизионная камера,
датчик телеметрической системы и т.п.), как правило, не могут быть непосредственно переданы по
радиоканалу. Дело не только в том, что эти сигналы недостаточно велики по амплитуде. Гораздо
существеннее их низкочастотность. Чтобы осуществить эффективную передачу сигналов в какой-либо
среде, необходимо перенести спектр этих сигналов из низкочастотной области в область достаточно высоких
частот. Данная процедура называется в радиотехнике – модуляция.
Понятие несущего колебания. Идея способа, позволяющего переносить спектр сигнала в область
высоких частот, заключается в следующем. Прежде всего в передатчике формируется вспомогательный
высокочастотный сигнал, называемый несущим колебанием. Его математическая модель uнес=f(t; a1, a2, …,
am) такова, что имеется некоторая совокупность параметров a1, a2, …, am, определяющих форму этого
колебания. Пусть s(t) – некоторое низкочастотное сообщение, подлежащее передаче по радиоканалу. Если,
по крайней мере, один из указанных параметров изменяется во времени пропорционально передаваемому
сообщению, то несущее колебание принимает новое свойство – оно несет в себе информацию, которая
первоначально была заключена в сигнале s(t).
Физический процесс управления параметрами несущего колебания и является модуляцией.
В радиотехнике широкое распространение получили системы модуляции, использующие в качества
несущего простое гармоническое колебание:
uнес(t)=U cos(ωt+φ),
(3.1)
имеющее три свободных параметра U, ω и φ.
Изменяя во времени тот или иной параметр, можно получать различные виды модуляции.
2

3.

Принцип амплитудной модуляции.
Если переменной оказывается амплитуда сигнала U(t), причем остальные два параметра ω и φ
неизменны, то имеется амплитудная модуляция несущего колебания. Форма записи амплитудномодулированного сигнала, или АМ-сигнала, такова:
uАМ(t)=U(t)cos(ω0t+φ0).
(3.2)
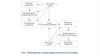
Осциллограмма АМ-сигнала имеет характерный вид (рис. 3.1). Обращает на себя внимание симметрия
графика относительно оси времени. В соответствии с формулой (3.2) АМ-сигнал есть произведение
огибающей U(t) и гармонического заполнения cos(ω0t+φ0). В большинстве практически интересных случаем
огибающая изменяется во времени гораздо медленнее, чем высокочастотное заполнение.
Рисунок 3.1. АМ-сигналы при различных глубинах модуляции: а – неглубокая модуляция, б –
глубокая модуляция, в – перемодуляция.
3

4.

При амплитудной модуляции связь между огибающей U(t) и модулирующим полезным сигналом s(t)
принято определять следующим образом:
U(t)= Um [1+M*s(t)].
(3.3)
Здесь Um – постоянный коэффициент, равный амплитуде несущего колебания в отсутствии модуляции; М
– коэффициент амплитудной модуляции.
Величина М характеризует глубину амплитудной модуляции. Смысл этого термина поясняется
осциллограммами на рисунке 3.1.а-в.
При малой глубине модуляции относительное изменение огибающей невелико, то есть |М*s(t)|<< 1 во все
моменты времени независимо от формы сигнала s(t).
Если же есть моменты времени, когда сигнал s(t) достигает экстремальных значений, имеются
приближенные равенства М*smax(t)|≈1 или М*smin(t)|≈ –1, то говорят о глубокой амплитудной модуляции.
Иногда вводят дополнительно относительный коэффициент модуляции вверх
U max U m
M
B
или относительный коэффициент модуляции вниз
Um
U m U min
M
.
H
Um
АМ-сигналы с малой глубиной модуляции в радиоканалах нецелесообразны ввиду неполного
использования мощности передатчика. В то же время 100%-ная модуляция вверх (MB=1) в два раза повышает
амплитуду колебаний при пиковых значениях модулирующего сообщения.
4

5.

Дальнейший рост этой амплитуды, как правило, приводит к нежелательным искажениях из-за перегрузки
выходных каскадов передатчика. Не менее опасна слишком глубокая амплитудная модуляция вниз. На
рисунке 3.1. в изображена перемодуляция (MН>1). Здесь форма огибающей перестает повторять форму
модулирующего сигнала.
Однотональная амплитудная модуляция. Простейший АМ-сигнал может быть получен в случае, когда
модулирующим низкочастотным сигналом является гармоническое колебание с частотой Ω. Такой сигнал
uAM t U m cos 1 M cos t 0 cos 0t 0
(3.4)
называется однотоналъным АМ-сигналом.
Выясним, можно ли такой сигнал представить как сумму простых гармонических колебаний с
различными частотами. Используя известную тригонометрическую формулу произведения косинусов, из
выражения (3.4) сразу получаем
U M
U M
uAM t U m cos 0t 0 m cos 0 t 0 0 m cos 0 t 0 0 . (3.5)
2
2
Формула (3.5) устанавливает спектральный состав однотонального АМ-сигнала. Принята следующая
терминология: ω0 – несущая частота, ω0 + Ω – верхняя боковая частота, ω0 – Ω – нижняя боковая частота.
Строя по формуле (3.5) спектральную диаграмму однотонального АМ-сигнала, следует прежде всего
обратить внимание на равенство амплитуд верхнего и нижнего боковых колебаний, а также на симметрию
расположения этих спектральных составляющих относительно несущего колебания.
Энергетические характеристики АМ-сигнала. Рассмотрим вопрос о соотношении мощностей
несущего и боковых колебаний. Источник однотонального АМ-сигнала эквивалентен трем последовательно
включенным источникам гармонических колебаний:
5

6.

uHEC t U m cos 0t 0 ,
UmM
UmM
uВБ t
cos 0 t 0 0 , uНБ t
cos 0 t 0 0 .
2
2
Положим для определенности, что это источники ЭДС, соединенные последовательно и нагруженные на
единичный резистор. Тогда мгновенная мощность АМ-сигнала будет численно равна квадрату суммарного
напряжения:
2
2
2
pAM t uAM
uВБ
uНБ
2uНЕСuВБ 2uНЕСuНБ 2uВБuНБ .
(3.6)
Чтобы найти среднюю мощность сигнала, величину p(t) необходимо усреднить по достаточно большому
T
отрезку времени Т:
1
pАМ lim p t dt.
T T
0
Легко убедиться в том, что при усреднении все взаимные мощности дадут нулевой результат, поэтому
средняя мощность АМ-сигнала окажется равной сумме средних мощностей несущего и боковых колебаний:
Отсюда следует, что
U m2 U m2 M 2
pAM pHEC pВБ pНБ
.
2
2
pВБ pНБ
M2
.
pHEC
2
(3.7)
(3.8)
Так, даже при 100%-ной модуляции (М = 1) доля мощности обоих боковых колебаний составляет всего
лишь 50% от мощности смодулированного несущего колебания.
6

7.

Поскольку информация о сообщении заключена в боковых колебаниях, можно отметить неэффективность
использования мощности при передаче АМ-сигнала.
Амплитудная модуляция при сложном модулирующем сигнале. На практике однотональные АМсигналы используются редко. Гораздо более реален случай, когда модулирующий низкочастотный сигнал
имеет сложный спектральный состав. Математической моделью такого сигнала может быть, например,
N
тригонометрическая сумма
(3.9)
s t i cos it i .
i 1
Здесь частоты Ωi образуют упорядоченную возрастающую последовательность Ω1 < Ω2 <… < Ω N, в то
время как амплитуды αi и начальные фазы Фi произвольны.
Подставив формулу (3.9) в (3.3), получим
N
uAM t U m 1 M i cos it i cos 0t 0 .
i 1
(3.10)
Введем совокупность парциальных (частичных) коэффициентов модуляции
Mi=Mαi
(3.11)
и запишем аналитическое выражение сложномодулированного (многотонального) АМ-сигнала в форме,
которая обобщает выражение (3.4):
N
uAM t U m 1 M i cos it i cos 0t 0 .
i 1
(3.12)
Спектральное разложение проводится так же, как и для однотонального АМ-сигнала:
7

8.

N
N
UmM i
U M
uAM t U m cos 0t 0
cos 0 i t 0 i m i cos 0 i t 0 i
2
2
i 1
i 1
(3.13)
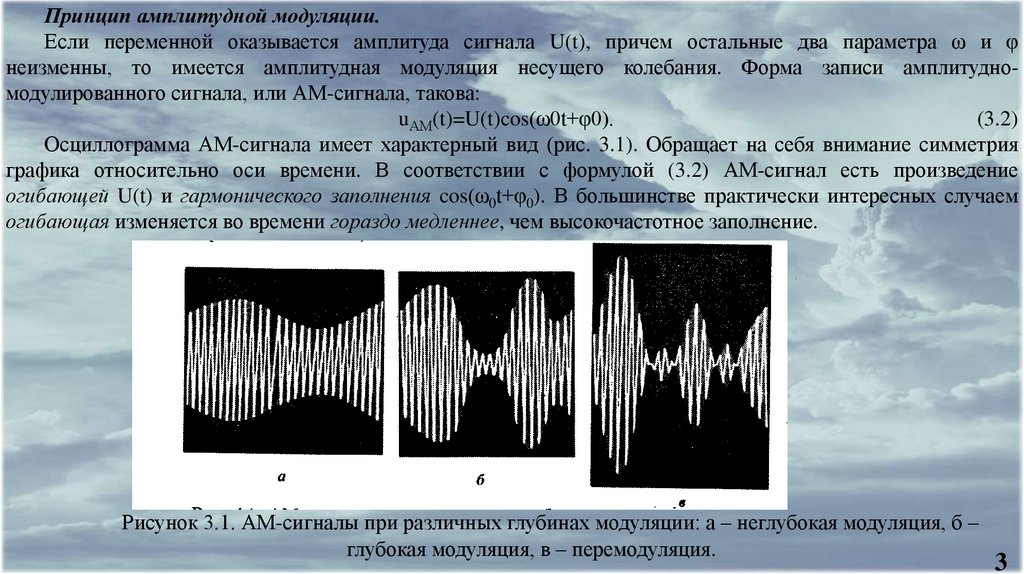
На рис. 3.2, а изображена спектральная диаграмма модулирующего сигнала s(t), построенная в
соответствии с формулой (3.9). Рис. 3.2,6 воспроизводит спектральную диаграмму многотонального АМсигнала, отвечающего этому модулирующему колебанию.
Рисунок 3.2. Спектральные диаграммы:
а – модулирующего сигнала;
б – АМ-сигнала при многотональной
модуляции
Итак, в спектре сложномодулированного АМ-сигнала, помимо несущего колебания, содержатся группы
верхних и нижних боковых колебаний. Спектр верхних боковых колебаний является масштабной копией
спектра модулирующего сигнала, сдвинутой в область высоких частот на величину ω0. Спектр нижних
боковых колебаний также повторяет спектральную диаграмму сигнала s(t), но располагается зеркально
относительно несущей частоты ω0.
Из сказанного следует важный вывод: ширина спектра АМ-сигнала равна удвоенному значению
наивысшей частоты в спектре модулирующего низкочастотного сигнала.
8

9.

Амплитудно-манипулированные сигналы. Важным классом многотональных АМ-сигналов являются
так называемые манипулированные сигналы. В простейшем случае это – последовательности
радиоимпульсов, отделенных друг от друга паузами. Такие сигналы используются в радиотелеграфии и в
системах передачи дискретной информации по радиоканалам.
Если s (t) – функция, в каждый момент времени принимающая значение либо 0, либо 1, то амплитудноманипулированный сигнал представляется в виде
uMAH t U m s t cos 0t 0
(3.14)
Пусть, например, функция s(t) отображает периодическую последовательность видеоимпульсов. Считая,
что амплитуда этих импульсов А = 1, на основании (3.14) имеем при φ0 = 0:
sin
n
q
Um
Um
uMAH t
cos 0t
q
q n 1 n
q
где q – скважность последовательности.
sin
n
q
Um
cos 0 n 1 t
q n 1 n
q
cos 0 n 1 t
(3.15)
Векторная диаграмма АМ-сигнала. Иногда полезным может оказаться графическое изображение АМсигнала посредством суммы векторов, вращающихся в комплексной плоскости. Для простоты рассмотрим
однотональную модуляцию. Мгновенное значение несущего колебания uHEC t U m cos 0t 0 есть проекция
неподвижного во времени вектора U HEC U m exp j 0 на ось отсчета углов, которая вращается вокруг начала
координат с угловой скоростью ω0 в направлении часовой стрелки (рис. 3.3).
Верхнее боковое колебание отображается на диаграмме вектором U ВБ длиной UmM/2, причем его
фазовый угол при t = 0 равен сумме начальных фаз несущего и модулирующего сигналов [см. формулу (3.5)].
9

10.

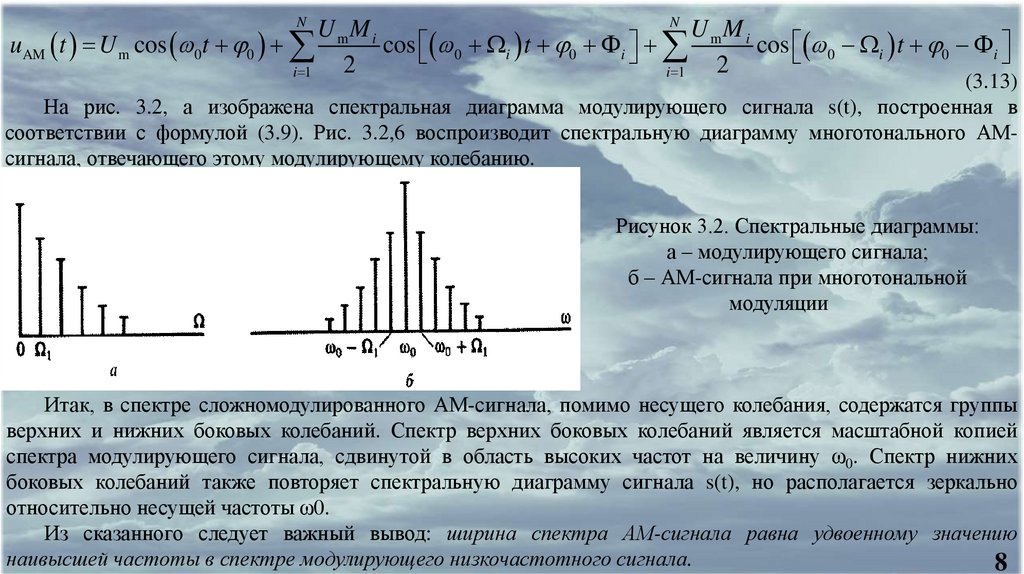
Такой же вектор для нижнего бокового колебания
отличается лишь знаком в выражении для его фазового угла.
Итак, на комплексной плоскости необходимо построить
сумму трех векторов
j 0 0
j 0 0
j 0
U HEC U m e
, U ВБ U m e
, U НБ U m e
Легко видеть, что эта сумма будет ориентирована вдоль
вектора U НЕС Мгновенное значение АМ-сигнала при t = 0
окажется равным проекции конца результирующего вектора
на горизонтальную ось (рис. 3.3, а).
Рисунок 3.3 Векторные диаграммы
однотонального АМ-сигнала: a - при t = 0; б
– при t > 0.
С течением времени, помимо отмеченного вращения оси отсчета углов, будут наблюдаться следующие
трансформации чертежа (рис. 3.3,б): 1) вектор U ВБ
будет вращаться вокруг точки своего приложения с
угловой скоростью Ω в направлении против часовой стрелки, поскольку фаза верхнего бокового колебания
(ω0+ Ω)t + φ0+Ф0 возрастает быстрее фазы несущего сигнала; 2) вектор U НБ будет вращаться также с угловой
скоростью Ω, но в противоположном направлении.
Строя суммарный вектор U и проецируя его на ось отсчета углов, можно найти мгновенные значения
uAM(t) в любой момент времени.
Балансная амплитудная модуляция. Как было показано, значительная доля мощности обычного АМсигнала сосредоточена в несущем колебании. Для более эффективного использования мощности передатчика
можно формировать АМ-сигналы с подавленным несущим колебанием, реализуя так называемую балансную
амплитудную модуляцию.
10
.

11.

На основании формулы (3.4) представление однотонального АМ-сигнала с балансной мрдуляцией таково:
uБМ t U m M cos t 0 cos 0t 0
UmM
U M
cos 0 t 0 0 m cos 0 t 0 0 . (3.16)
2
2
Имеет место перемножение двух сигналов – модулирующего и несущего. Колебания вида (3.16) с
физической точки зрения являются биениями двух гармонических сигналов с одинаковыми амплитудами
UmM/2 и частотами, равными верхней и нижней боковым частотам.
При многотональной балансной модуляции аналитическое выражение сигнала принимает вид
Um M
Um M
uБМ t
M i cos 0 i t 0 i .
M i cos 0 i t 0 i 2
2 i 1
i 1
(3.17)
Как и при обычной амплитудной модуляции, здесь наблюдаются две симметричные группы верхних и
нижних боковых колебаний.
Если рассмотреть осциллограмму биений, может показаться неясным, почему в спектре этого сигнала
нет несущей частоты, хотя налицо присутствие высокочастотного заполнения, изменяющегося во времени
именно с этой частотой.
Рисунок 3.3.
Осциллограмма сигнала с
балансной модуляцией.
11

12.

Дело в том, что при переходе огибающей биений через нуль фаза высокочастотного заполнения скачком
изменяется на 180°, поскольку функция соs(Ωt+Ф0) имеет разные знаки слева и справа от нуля. Если такой
сигнал подать на высокодобротную колебательную систему (например, LC-контур), настроенную на частоту
ω0, то выходной эффект будет очень мал, стремясь к нулю при возрастании добротности. Колебания в
системе, возбужденные одним периодом биений, будут гаситься последующим периодом.
Балансная амплитудная модуляция, несмотря на свои достоинства, не нашла широкого применения в
технике радиовещания и связи.
Однополосная амплитудная модуляция. Еще более интересное усовершенствование принципа обычной
амплитудной модуляции заключается в формировании сигнала с подавленной верхней или нижней боковой
полосой частот.
Сигналы с одной боковой полосой (ОБП-или SSB-сигналы – от англ. single sideband) по внешним
характеристикам напоминают обычные АМ-сигналы. Например, однотональный ОБП-сигнал с подавленной
нижней боковой частотой записывается в виде
UmM
uОБП t U m cos 0t 0
cos 0 t 0 0 .
2
Проводя тригонометрические преобразования, получаем
UmM
U M
cos t 0 cos 0t 0 m sin t 0 sin 0t 0
2
2
U M
M
U m 1 cos t 0 cos 0t 0 m sin t 0 sin 0t 0 .
2
2
uОБП t U m cos 0t 0
12

13.

Два последних слагаемых представляют собой произведение двух функций, одна из которых изменяется
во времени медленно, а другая – быстро. Принимая во внимание, что «быстрые» сомножители находятся по
отношению друг к другу во временной квадратуре, вычисляем медленно изменяющуюся огибающую ОБПсигнала:
U t U m
2
2
2
M
M
M
2
1
cos
t
sin
t 0 U m 1 M cos t 0 .
0
2
4
4
(3.18)
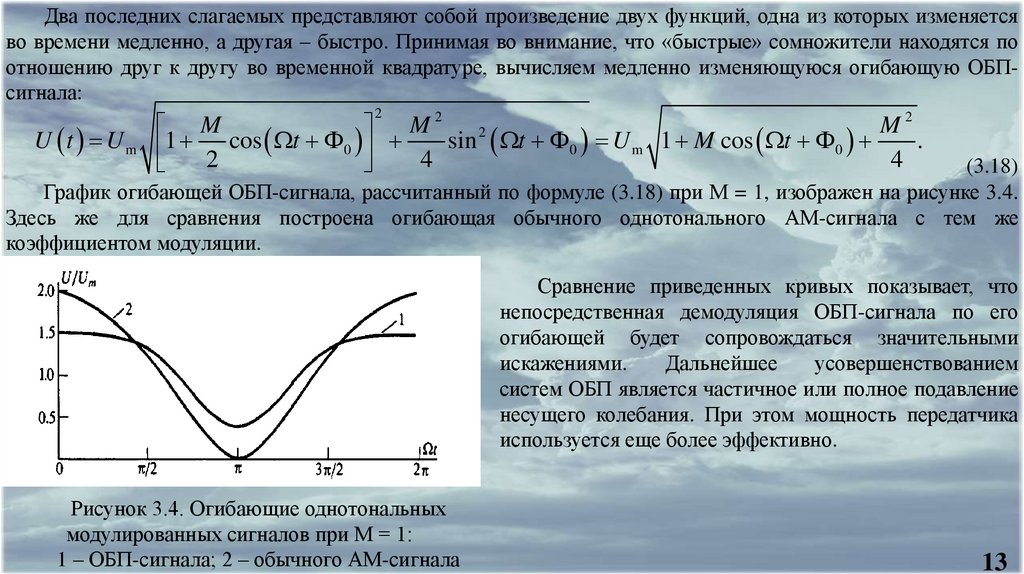
График огибающей ОБП-сигнала, рассчитанный по формуле (3.18) при М = 1, изображен на рисунке 3.4.
Здесь же для сравнения построена огибающая обычного однотонального АМ-сигнала с тем же
коэффициентом модуляции.
Сравнение приведенных кривых показывает, что
непосредственная демодуляция ОБП-сигнала по его
огибающей будет сопровождаться значительными
искажениями.
Дальнейшее
усовершенствованием
систем ОБП является частичное или полное подавление
несущего колебания. При этом мощность передатчика
используется еще более эффективно.
Рисунок 3.4. Огибающие однотональных
модулированных сигналов при М = 1:
1 – ОБП-сигнала; 2 – обычного АМ-сигнала
13

14.

Сигналы с угловой модуляцией. Будем изучать модулированные радиосигналы, которые получаются за
счет того, что в несущем гармоническом колебании uНЕС (t)=Umcos(ωt + φ) передаваемое сообщение s(t)
изменяет либо частоту ω, либо начальную, фазу амплитуда Um остается неизменной. Поскольку аргумент
гармонического колебания ψ(t) = ωt + φ, называемый полной фазой, определяет текущее значение фазового
угла, такие сигналы получили название сигналов с угловой модуляцией.
Виды угловой модуляции. Предположим вначале, что полная фаза ψ(t) связана с сигналом s(t)
зависимостью
t 0t ks t
(3.19)
где ω0 – значение частоты в отсутствие полезного сигнала; k – некоторый коэффициент пропорциональности.
Модуляцию, отвечающую соотношению (3.19), называют фазовой модуляцией (ФМ):
uФМ t U m cos 0t ks t .
(3.20)
Если сигнал s(t) = 0, то ФМ-колебание является
простым гармоническим колебанием. С увеличением
значений сигнала s(t) полная фаза ψ(t) растет во времени
быстрее, чем по линейному закону. При уменьшении
значений модулирующего сигнала происходит спад
скорости роста ψ(t) во времени.
На рис. 3.5 показано построение графика ФМ-сигнала.
Рисунок 3.5. Фазовая модуляция:
1 – модулирующий низкочастотный сигнал; 2 –
немодулированное гармоническое колебание; 3 – сигнал с
фазовой модуляцией
14

15.

В моменты времени, когда сигнал s(t) достигает экстремальных значений, абсолютный фазовый сдвиг
между ФМ-сигналом и смодулированным гармоническим колебанием оказывается наибольшим. Предельное
значение этого фазового сдвига называют девиацией фазы Δψ. В общем случае, когда сигнал s(t) изменяет
знак, принято различать девиацию фазы вверх ΔψВ= ksmax и девиацию фазы вниз Δψн= ksmin.
На векторной диаграмме изображающий вектор постоянной длины будет совершать вращение с
непостоянной угловой скоростью. Мгновенная частота ω(t) сигнала с угловой модуляцией определяется как
первая производная от полной фазы по времени:
d
(3.21)
t
,
так что
dt
t
t d const.
(3.22)
При частотной модуляции сигнала (ЧМ) между величинами s(t) и ω(t) имеется связь вида:
Поэтому:
t 0 ks t .
(3.23)
t
uЧМ t U m cos 0t k s d .
(3.24)
Естественными параметрами ЧМ-сигнала общего вида в соответствии с формулой (3.23) являются
девиация частоты вверх ΔωВ= ksmax и девиация частоты вниз ΔωН = ksmin.
15

16.

Если s (t) – достаточно гладкая функция, то внешне осциллограммы ФМи ЧМ-сигналов не отличаются. Однако имеется принципиальная разница:
фазовый сдвиг между ФМ-сигналом и немодулированным колебанием
пропорционален s(t), в то время как для ЧМ-сигнала этот сдвиг
пропорционален интегралу от передаваемого сообщения.
Однотональные сигналы с угловой модуляцией. Анализ ФМ- и ЧМРисунок 3.6. Осциллограмма сигналов с математической точки зрения гораздо сложнее, чем исследование
типичного сигнала с угловой АМ-колебаний. Поэтому основное внимание будет уделено простейшим
однотональным сигналам.
модуляцией.
В случае однотонального ЧМ-сигнала мгновенная частота
t 0 cos t 0 ,
где Δω – девиация частоты сигнала. На основании формулы (3.22) полная фаза такого сигнала
t 0t
sin t 0 0 ,
где φ0– некоторый постоянный фазовый угол.
Отсюда видно, что величина
m
(3.25)
называемая индексом однотональной угловой модуляции, представляет собой девиацию фазы такого сигнала,
выраженную в радианах.
Для краткости положим, что неизменные во времени фазовые углы φ0=Ф0=0, и выразим мгновенное
значение ЧМ-сигнала в виде
16

17.

uЧМ t U m cos 0t m sin t .
(3.26)
Аналитическая форма записи однотонального ФМ-сигнала будет аналогичной. Однако нужно иметь в
виду следующее: ЧМ- и ФМ-сигналы ведут себя по-разному при изменении частоты модуляции и амплитуды
модулирующего сигнала.
При частотной модуляции девиация частоты Δω0 пропорциональна амплитуде низкочастотного сигнала. В
то же время величина Δω0 не зависит от частоты модулирующего сигнала. В случае фазовой модуляции ее
индекс m оказывается пропорциональным амплитуде низкочастотного сигнала независимо от его частоты.
Как следствие этого, девиация частоты при фазовой модуляции в соответствии с формулой (3.25) линейно
увеличивается с ростом частоты.
Спектральное разложение ЧМ- и ФМ-сигналов при малых индексах модуляции. Задачу о
представлении сигналов с угловой модуляцией посредством суммы гармонических колебаний несложно
решить в случае, когда m<<1. Для этого преобразуем формулу (3.26) следующим образом:
u t U m cos 0t m sin t U m cos m sin t cos 0t U m sin m sin t sin 0t
(3.27)
Поскольку индекс угловой модуляции мал, воспользуемся приближенными равенствами
cos m sin t 1; sin m sin t m sin t.
На основании этого из равенства (3.27) получаем
mU m
mU m
u t U m cos 0t
cos 0 t
cos 0 t.
2
2
(3.28)
Таким образом, показано, что при m <<1 в спектре сигнала с угловой модуляцией содержатся несущее
колебание и две боковые составляющие (верхняя и нижняя) на частотах ω0+Ω и ω0–Ω. Индекс m играет здесь
такую же роль, как коэффициент амплитудной модуляции М [ср. с формулой (3.5)].
17

18.

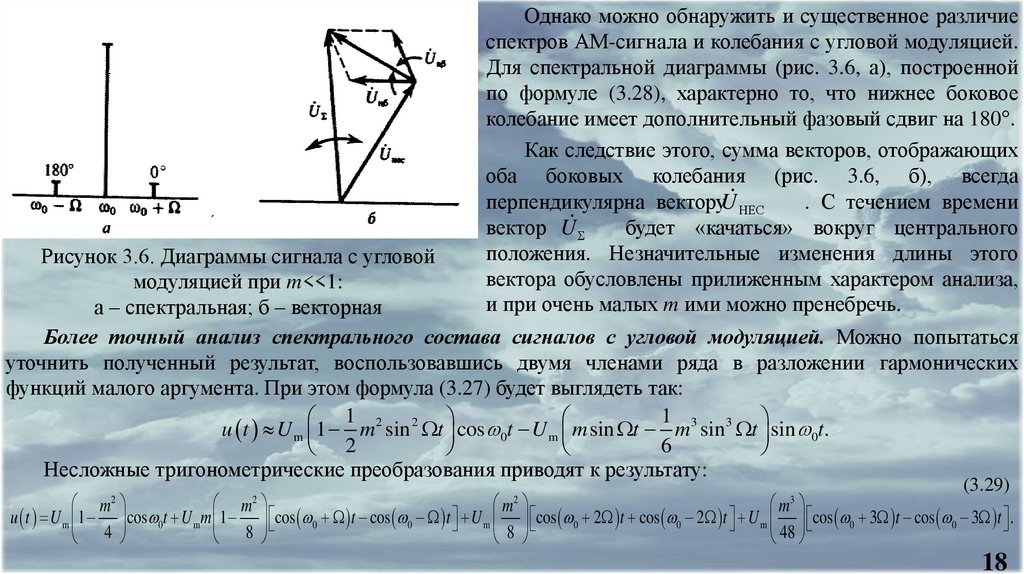
Однако можно обнаружить и существенное различие
спектров АМ-сигнала и колебания с угловой модуляцией.
Для спектральной диаграммы (рис. 3.6, а), построенной
по формуле (3.28), характерно то, что нижнее боковое
колебание имеет дополнительный фазовый сдвиг на 180°.
Как следствие этого, сумма векторов, отображающих
оба боковых колебания (рис. 3.6, б), всегда
перпендикулярна векторуU НЕС
. С течением времени
вектор U
будет «качаться» вокруг центрального
положения. Незначительные изменения длины этого
вектора обусловлены прилиженным характером анализа,
и при очень малых m ими можно пренебречь.
Рисунок 3.6. Диаграммы сигнала с угловой
модуляцией при m<<1:
а – спектральная; б – векторная
Более точный анализ спектрального состава сигналов с угловой модуляцией. Можно попытаться
уточнить полученный результат, воспользовавшись двумя членами ряда в разложении гармонических
функций малого аргумента. При этом формула (3.27) будет выглядеть так:
1
1
u t U m 1 m2 sin 2 t cos 0t U m m sin t m3 sin 3 t sin 0t.
6
2
Несложные тригонометрические преобразования приводят к результату:
(3.29)
m
m
m
m
u t U m 1 cos 0t U m m 1 cos 0 t cos 0 t U m cos 0 2 t cos 0 2 t U m cos 0 3 t cos 0 3 t .
4
8
8
48
2
2
2
3
18

19.

Эта формула свидетельствует о том, что в спектре сигнала с однотональной угловой модуляцией, помимо
известных составляющих, содержатся также верхние и нижние боковые колебания, соответствующие
гармоникам частоты модуляции. Поэтому спектр такого сигнала сложнее спектра аналогичного АМ-сигнала.
Отметим также, что возникновение новых спектральных составляющих приводит к перераспределению
энергии по спектру. Так, из формулы (3.29) видно, что с ростом m амплитуда боковых составляющих
увеличивается, в то время как амплитуда несущего колебания уменьшается пропорционально множителю (1 –
m2/4).
Спектр сигнала с угловой модуляцией при произвольном значении индекса. Для простейшего случая
однотонального ЧМ- или ФМ-сигнала можно найти общее выражение спектра, справедливое при любом
значении индекса модуляции m.
В разделе курса математики, посвященном специальным функциям, доказывается, что экспонента exp
(jmsinx)с мнимым показателем специального вида, периодическая на отрезке –π ≤ х ≤π , разлагается в
комплексный ряд Фурье:
jm sin x
jkx
Jk m e ,
е
k
(3.30)
где m – любое вещественное число; Jk (m) – функция Бесселя k-го индекса от аргумента m.
Сравнивая формулы (3.30) и (3.27), а также подставляя х = Ωt, перепишем последнюю из указанных
формул так:
u t U m Re e j 0t e jm sin t U m Re e j 0t J k m e jk t .
k
(3.31)
Отсюда получаем следующую математическую модель ЧМ- или ФМ-сигнала с любым значением индекса
модуляции:
19

20.

u t U m J k m cos 0 k t.
(3.32)
Спектр однотонального сигнала с угловой модуляцией в общем случае содержит бесконечное число
составляющих, частоты которых равны ω0±kΩ; амплитуды этих составляющих пропорциональны значениям
Jk(m).
В теории функций Бесселя доказывается, что функции с положительными и отрицательными индексами
связаны между собой:
k
k
J k m 1 J k m .
Поэтому начальные фазы боковых колебаний с частотами ω0+kΩ и ω0–kΩ совпадают, если k – четное
число, и отличаются на 180°, если k – нечетное.
Для детального анализа и построения спектральных диаграмм необходимо знать поведение функций
Jk(m) при различных m в зависимости от k. На рис. 3.7 приведены графики двух функций Бесселя,
существенно различающихся своими индексами.
Можно заметить следующее: чем больше индекс функции Бесселя,
тем протяженнее область аргументов, при которых эта функция
очень мала.
Рисунок 3.7. Графики функций
Бесселя J (m) и J (m)
20

21.

Рисунок 3.8 Спектральные диаграммы сигнала с
угловой модуляцией
при двух значениях индекса m (амплитуды представлены в
относительном масштабе)
Важно отметить, что с ростом индекса модуляции расширяется полоса частот, занимаемая сигналом.
Обычно полагают, что допустимо пренебречь всеми спектральными составляющими с номерами k > m + 1.
Отсюда следует оценка практической ширины спектра сигнала с угловой модуляцией (с-1):
практ 2 m 1 .
(3.33)
Как правило, реальные ЧМ- и ФМ-сигналы характеризуются условием m>>1. В этом случае
практ 2m 2 .
Таким образом, сигнал с угловой модуляцией занимает полосу частот, приблизительно "равную
удвоенной девиации частоты. Как было выяснено, для передачи амплитудно-модулированного сигнала
требуется полоса частот, равная 2Ω, т. е. в т раз меньшая. Большая широкополосность ЧМ- и ФМ- сигналов
обусловливает их применимость для целей радиосвязи лишь на очень высоких частотах, в диапазонах
метровых и более коротких волн. Однако именно широкополосность приводит к гораздо большей
помехоустойчивости сигналов с угловой модуляцией по сравнению с АМ-сигналами.
21

22.

Как отмечалось, рост индекса модуляции приводит к перераспределению мощности в спектре
модулированного сигнала. В частности, если значение m выбрано таким, что J0(m)=0, то несущее колебание
на частоте ω0 в спектре будет отсутстствовать. Значения m, являющиеся корнями данного уравнения,
образуют бесконечную возрастающую последовательность чисел mυ (υ = 1, 2…– номер корня).
Угловая модуляция при негармоническом модулирующем сигнале. Интересная особенность колебаний с
угловой модуляцией проявляется в случае, когда модулирующий сигнал не является гармоническим.
Рассмотрим для простоты сигнал, промодулированный лишь двумя низкими частотами:
u t U m cos 0t m1 sin 1t m2 sin 2t U m cos m1 sin 1t m2 sin 2t cos 0t U m sin m1 sin 1t m2 sin 2t sin 0t.
(3.35)
Положим, что парциальные индексы модуляции m1 и m2 малы настолько, что можно пользоваться
приближенными выражениями для косинуса и синуса:
x2
cos x 1 ; sin x x.
2
Выполнив несколько громоздкие, но вполне элементарные тригонометрические преобразования,
представим исходный сигнал в виде суммы
22

23.

m12 m22
U m
u t U m 1
cos 0t m 1 cos 0 1 t cos 0 1 t
4
2
U m m2
U m m12
cos 0 2 t cos 0 2 t
cos 0 2 1 t cos 0 2 1 t
2
8
U m m22
cos 0 2 2 t cos 0 2 2 t
8
U m m1m2
cos 0 1 2 t cos 0 1 2 t cos 0 1 2 t cos 0 1 2 t
(3.36)
2
Спектральная диаграмма такого двухтонального сигнала изображена на рис. 3.9.
Следует обратить внимание на то, что в спектре рассматриваемого сигнала, помимо частот ω0±Ω1,
ω0±Ω2, ω0±2Ω1, ω0±2Ω2, присутствуют так называемые комбинационные частоты ω0±Ω1±Ω2с четырьмя
возможными знаками. Амплитуды этих составляющих зависят от произведения парциальных индексов
модуляции.
Можно показать, что в общем случае, когда угловая модуляция осуществляется группой низкочартотных
колебаний с частотами Ω1, Ω2,…,ΩN и парциальными индексами m1, m2,…,mN соответственно, спектральное
представление сигнала таково:
23

24.

Рисунок 3.9. Спектральная диаграмма сигнала с двухтональной угловой
u t U m ... J k1 m1 J k2 m2 ...J kN mN cos 0 k1 1 k2 2 ... k N N t
(3.37)
Таким образом, при прочих равных условиях спектр колебания со сложной угловой модуляцией гораздо
богаче спектра аналогичного АМ-сигнала. Подчеркивая взаимодействие отдельных составляющих
модулирующего сигнала, угловую, модуляцию, в отличие от амплитудной, иногда называют модуляцией
нелинейного типа.
k1 k2
k N
24

25.

Анализ свойств радиотехнических сигналов, применяемых в бортовом
радиоэлектронном оборудовании воздушных судов.
С формальной точки зрения, любую бортовую радиосистему можно рассматривать как совокупность
технических устройств, предназначенных для передачи и приема определенной информации. При этом
информация может иметь самую различную природу: быть значением температуры воздуха за бортом,
высотой полета ВС, количеством оставшегося топлива и т.д. Закладка информации в радиосигнал обычно
осуществляется путем модуляции (от лат. modulatio – размеренность) того или иного параметра сигнала.
Физический процесс управления параметрами несущего колебания является модуляцией.
Широкое распространение получили системы модуляции, использующие в качестве несущего простое
гармоническое колебание U(t)=U sin(ωt+φ), имеющее три свободных параметра U, ω и φ.
Амплитудно-модулированным (АМ) называется радиосигнал с переменной амплитудой
uАМ t U0 Аm sin 2 fMt sin 2 f0 0 .
(3.38)
При этом предполагается, что информативная динамика, будучи переведенной в значения напряжения,
задается некоторой (модулирующей) функцией UM(t). Зависимость UM(t) может иметь весьма произвольный
характер. Если функция UM(t) является гармонической
uАМ t U 0 Аm sin 2 f Mt ,
где U0 – среднее значение модулирующего напряжения, Am – амплитуда модулирующего напряжения, fm=1/Tm
– частота модулирующего колебания, то АМ сигнал запишем в виде
25

26.

uАМ t U0 Аm sin 2 fMt sin 2 f0 0 .
(3.39)
Чтобы найти спектр АМ сигнала (положим φ0=0), разложим этот сигнал на гармонические
составляющие. Используя известные тригонометрические соотношения, получим
m
uАМ t U 0 sin 2 f 0t cos 2 f 0 f Mt t cos 2 f 0 f Mt t ,
2
где m=Am/U0 – коэффициент глубины АМ.
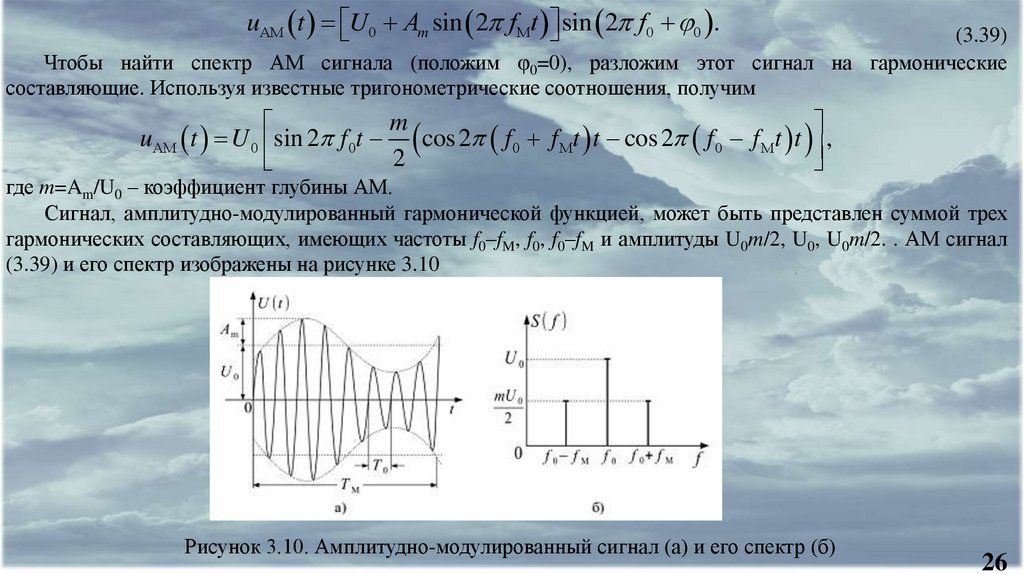
Сигнал, амплитудно-модулированный гармонической функцией, может быть представлен суммой трех
гармонических составляющих, имеющих частоты f0–fM, f0, f0–fM и амплитуды U0m/2, U0, U0m/2. . АМ сигнал
(3.39) и его спектр изображены на рисунке 3.10
Рисунок 3.10. Амплитудно-модулированный сигнал (а) и его спектр (б)
26

27.

Коэффициент глубины АМ m=Am/U0 является величиной безразмерной, меняющейся в пределах от 0
(отсутствие АМ) до 1 (предельная глубина неискаженной АМ) и характеризующей степень нормированной
(по отношению к U0) АМ сигнала.
Рисунок 3.11. Модулирующая последовательность видеоимпульсов (а) и последовательность
радиоимпульсов (б)
Рассмотрим случай, когда функция UM(t) является последовательностью видеоимпульсов (рис. 3.11 а).
Вид итогового (промодулированного) сигнала, который представляет собой последовательность так
называемых радиоимпульсов, показан на рисунке 3.11б. Значения длительности одного импульса τи и периода
повторения импульсов ТП являются параметрами импульсных последовательностей.
Для нахождения спектра последовательности радиоимпульсов используем разложение в ряд Фурье.
Разложение протяженного во времени, достаточно произвольного по форме, но периодического (с периодом
Т1) сигнала S(t) есть представление этого сигнала в виде суммы гармонических составляющих, частоты
которых кратны частоте дискретизации Ω1 (Ω1=2π/T1), а амплитуды Ak вычисляются согласно алгоритму
a0 m
a0 m
(3.40)
S t ak cos k 1t bk sin k 1t S t Ak cos k 1t k ,
2 k 1
2 k 1
27

28.

где
1 1
1 1
a0 1 1
b
ak S t cos k 1t d t , bk S t sin k 1t d t ,
S t d t , Ak ak2 bk2 , k arctg k .
2 T1 0
T1 0
T1 0
ak
T
T
T
Под спектром сигнала S(t) будем понимать только амплитудный спектр этого сигнала, зависимость
амплитуд Аk гармонических составляющих ряда Фурье от частот Ωk=kΩ1 указанных гармонических
составляющих. В качестве величины Т1 примем ТП.
Частотно-модулированным (ЧМ) называется сигнал с переменной частотой
uЧМ t U 0 sin 0 (t )t 0 .
(3.41)
где ω0(t) – закон изменения (модулирующая функция) частоты сигнала. Если модулирующая функция ω0(t)
изменяется по гармоническому закону
0 t 0 д sin Mt ,
(3.42)
где ω0 – несущая частота; ωд – девиация (максимальное отклонение частоты ω0(t) от частоты ω0) частоты; ΩM
– частота модуляции, то радиосигнал (3.42) можно представить в виде
uЧМ t U 0 sin 0 д sin Mt t 0 .
(3.43)
Спектр ЧМ сигнала (3.41) в общем случае вычисляется с помощью достаточно сложных (включающих
операции с функциями Бесселя) математических выражений. Можно отметить, что если отношение ωд/ΩM<1,
то внешний вид спектра такого ЧМ сигнала напоминает вид спектра АМ сигнала (рис. 3.10 б). Если в
качестве модулирующей функции ω0(t) используется линейная зависимость
0 t 0
д
t,
и
(3.44)
28

29.

где t – текущее время (t0≤t≤t0+τи), τи – длительность импульса, то результирующий радиоимпульс будет
называться линейно-частотно-модулированным.
Фазомодулированным (ФМ) называется сигнал с переменной фазой (φ(t) – закон изменения фазы
сигнала)
uФМ t U m sin 0t t .
(3.45)
Фазоманипулированный радиоимпульс показан на рисунке 3.12.
Значения фаз внутри радиоимпульса и периодичность их
изменения при внутриимпульсной фазовой модуляции могут
быть достаточно произвольными, однако на практике
наиболее часто весь радиоимпульс длительности τи
разбивается на целое число смежных дискретов равной
длительности τд. Частоты во всех дискретах одинаковы и
равны ω0, изменяются (в соответствии с модулирующей
функцией) лишь значения начальных фаз φ0 частоты ω0 – от
Рисунок 3.12 Фазоманипулированный сигнал. одного дискрета к другому.
В большинстве случаев начальные φ0 фазы принимают только 2 значения: 0о и 180о (с технической точки
зрения этот вариант наиболее легко реализуем) – сигнал называется фазоманипулированным либо
фазокодоманипулированным (последовательность 0о и 180о задается специальным кодовым словом).
В системах, использующих цифровые методы передачи информации, информация закладывается в
параметры кодирования дискретных сигналов: временные параметры (длительность импульсов, их временная
расстановка), частотное заполнение импульсов, фазовые соотношения в кодовой последовательности
сигналов и т.п.
29

30.

Литература для самостоятельного изучения:
1. Баскаков С.И. Радиотехнические цепи и сигналы – М.:Высшая школа 2000г., 462стр.
2. Гоноровский И.С Радиотехнические цепи и сигналы. – М.: Дрофа, 2006г, 722стр.
3. Стукалов С.Б. Теория радиотехнических сигналов. Детерминированные сигналы. Учебное пособие.
Москва, ООО «ИПП «ИНСОФТ», 2017 г. 68 с.
4. Леньшин, А.В., Тихомиров Н.М., ПоповС.А. Бортовые радиоэлектронные системы. Основы построения.
Воронеж : «Научная книга», 2021г.,486 с.
5. А.А. Сосновский, И.А. Хаймович. Радиоэлектронное оборудование летательных аппаратов. Справочник
специалиста. Москва.: Транспорт, 1987г., 256с.
6. Никольский Б.А. Бортовые радиоэлектронные система – Самара: СГАУ 2013г, 417стр.
30