Similar presentations:
Неоднозначное и однозначное соотнесение таблицы и графа
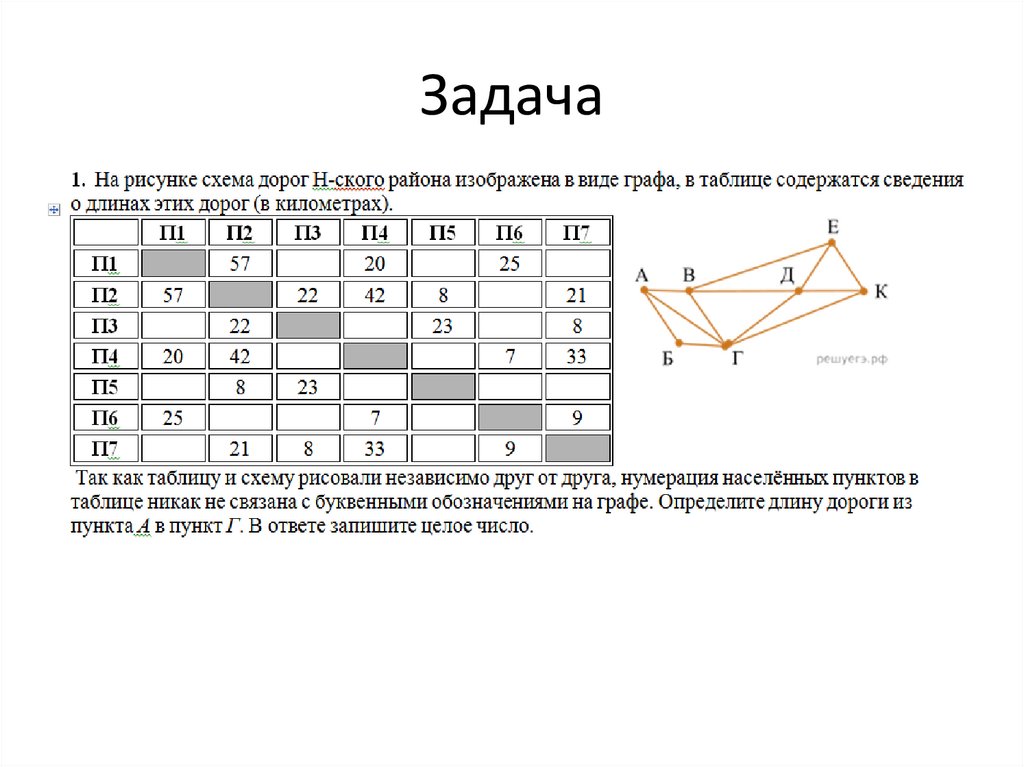
1.
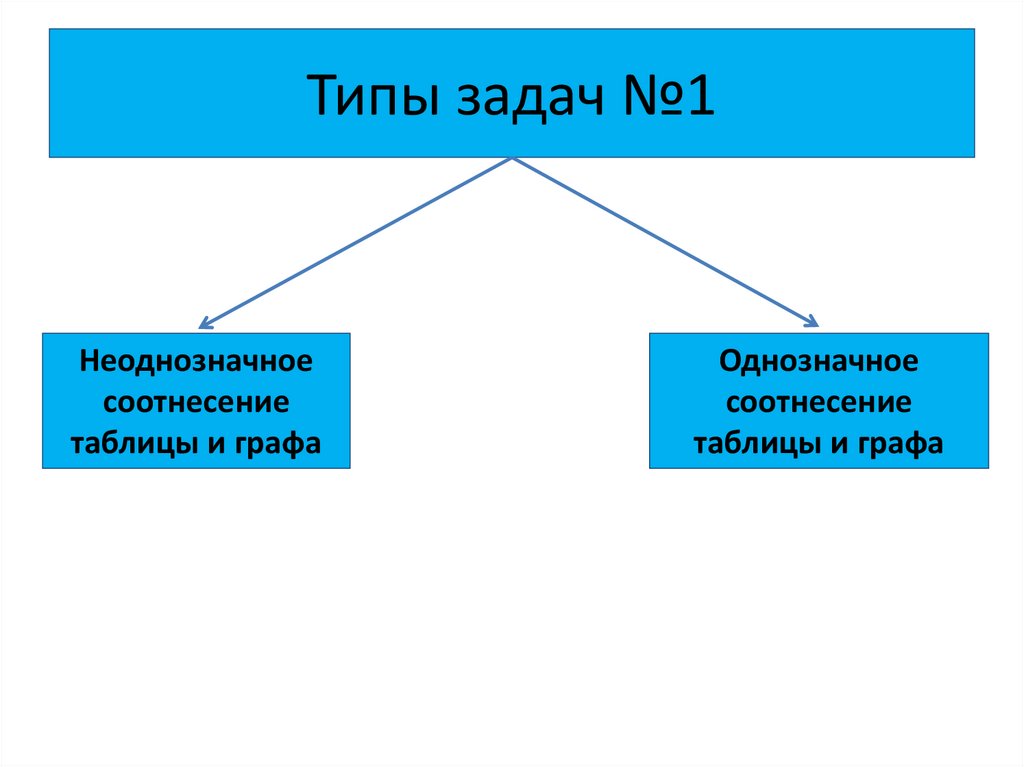
Типы задач №1Неоднозначное
соотнесение
таблицы и графа
Однозначное
соотнесение
таблицы и графа
2.
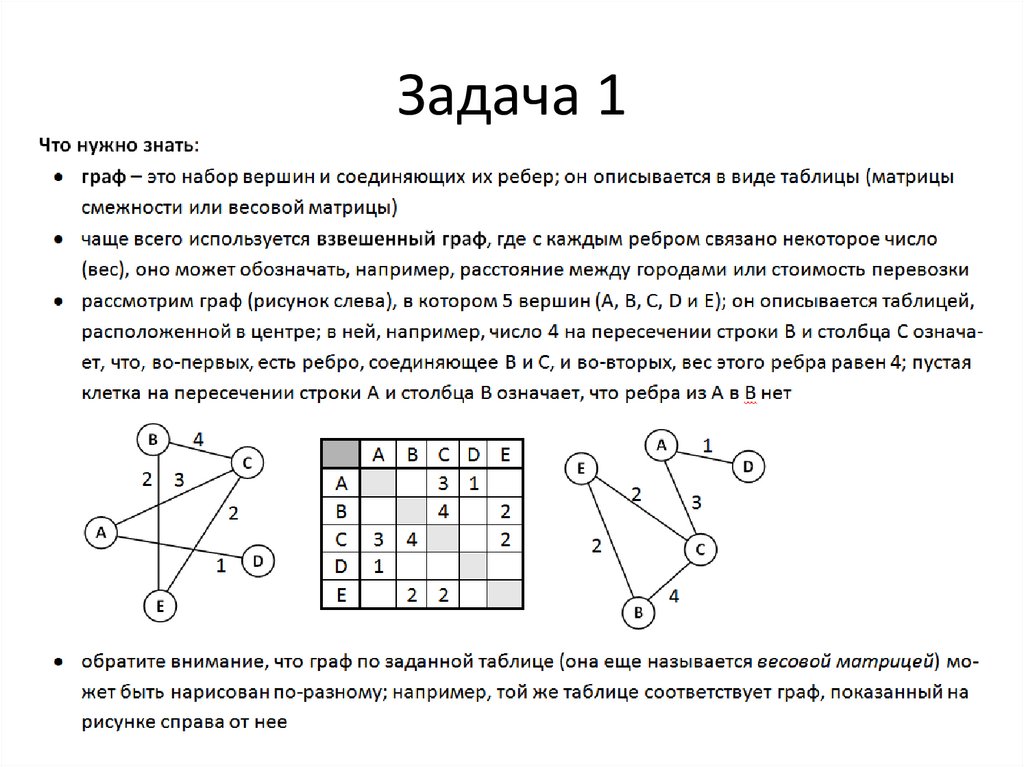
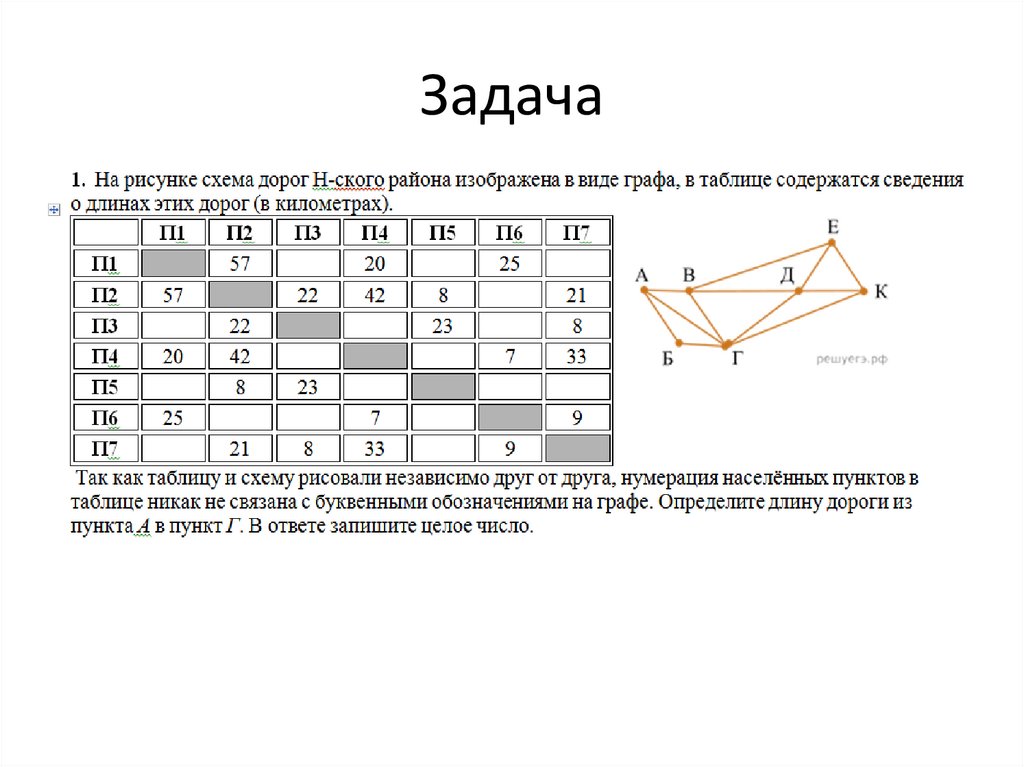
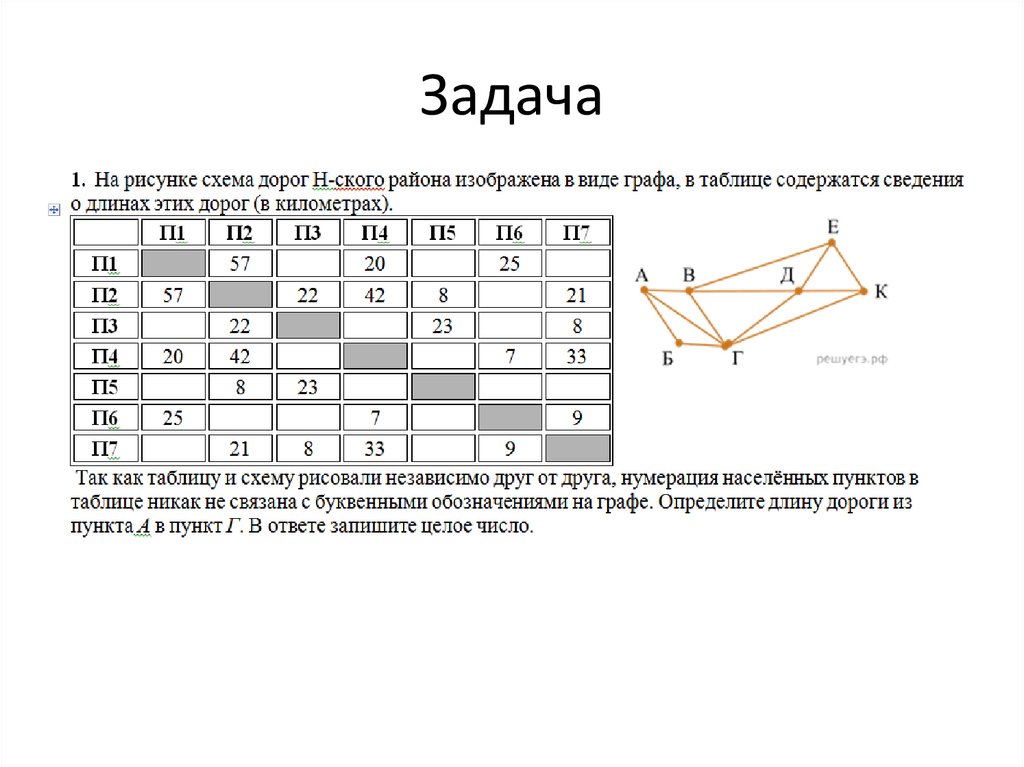
Задача 13.
Задача4.
Задача5.
Задача6.
Типы задач №2Сопоставление столбцов таблицы истинности и
переменных
7.
теория8.
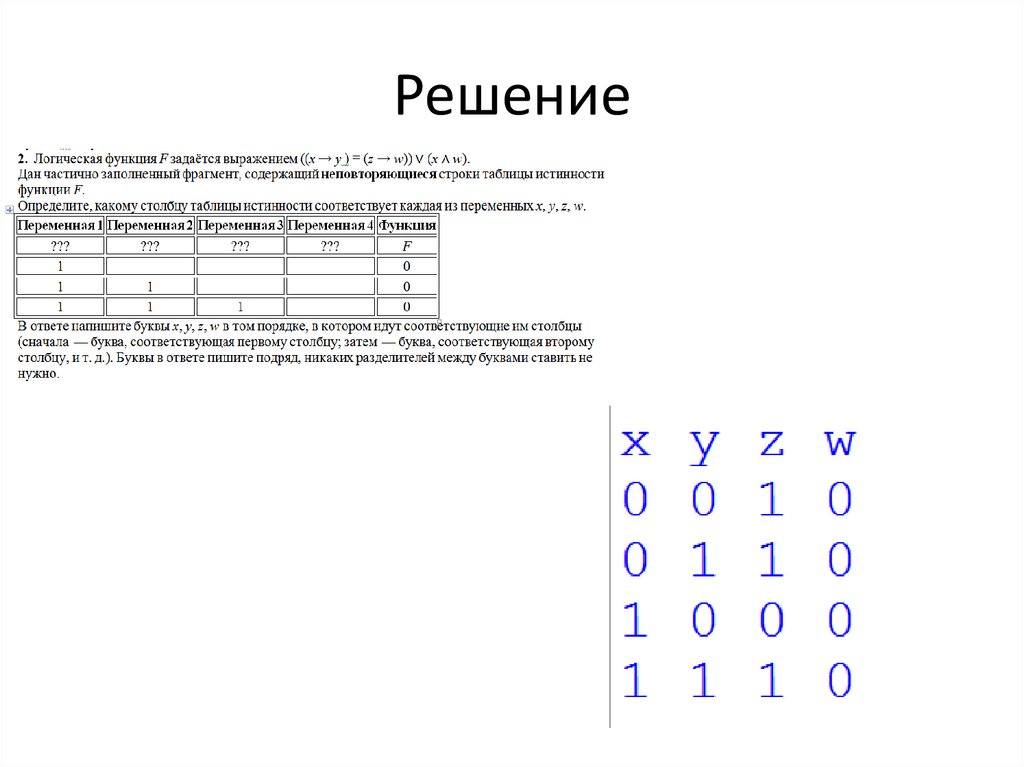
Задача 29.
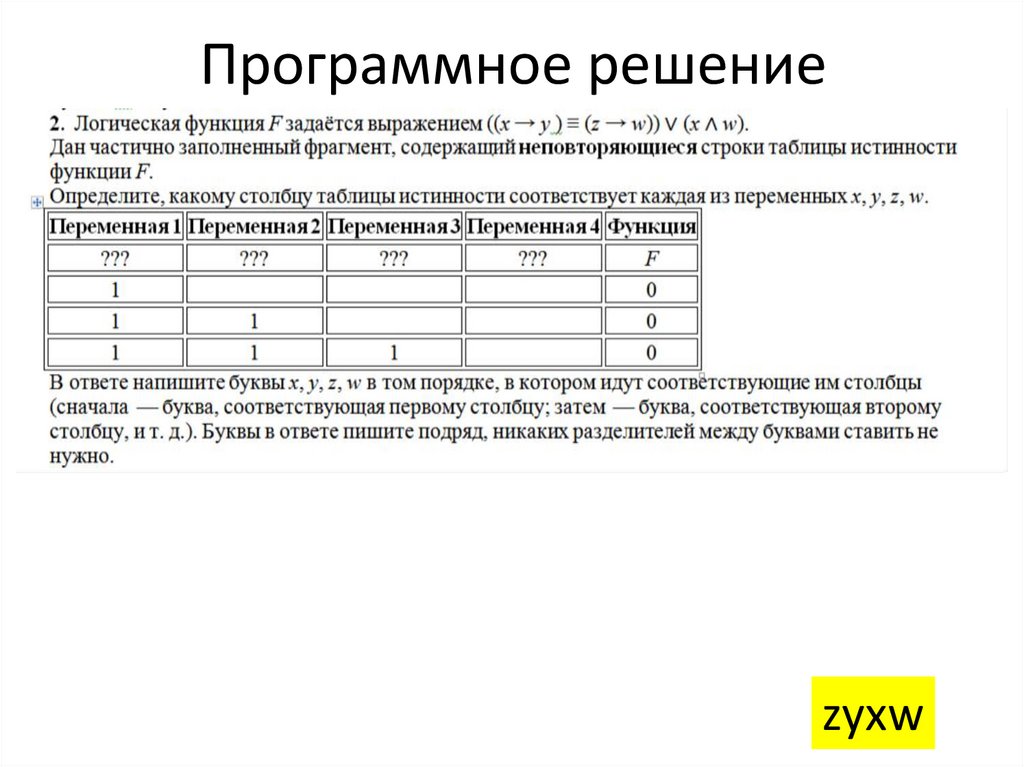
Задача 210.
Программный способ• поскольку во время компьютерного экзамена есть возможность использовать
среды программирования, для построения частичной таблицы истинности
(всех строк, при которых F=1) можно написать переборную программу на
Python
• перебор выполняем во вложенном цикле:
for x in 0, 1:
for y in 0, 1:
for z in 0, 1:
for w in 0, 1:
# вычисление функции F
# вывод (x, y, z, w), если F=1
11.
Анализ• для вычисления значения функции необходимо понимать, как логические
операторы записываются на языке программирования; в Python их можно
реализовать следующим образом:
∧
конъюнкция
and
для языков, где логическое значение True воспринимается как 1, а
False – как 0, можно использовать обычное умножение *
∨
дизъюнкция
or
¬
отрицания
not()
≡
тождество
==
⊕
строгая дизъюнкция
!=
→
импликация – для импликации в python оператора нет, но
импликацию можно преобразовать в дизъюнкцию; например, a → b
можно записать как ¬a ∨ b, а это в свою очередь записать как not(a)or
b, not a or b или a <= b
• Запишем нашу функцию на языке программирования:
F = (x or y) and not(y == z) and not(w)
12.
Решениеdef f(x,y,z,w):
return ( (x <= y) == (z <=w)) or (x and w)
print('x y z w')
for x in 0, 1:
for y in 0, 1:
from itertools import*
for z in 0, 1:
def f(x,y,z,w):
for w in 0, 1:
return ( (x <= y) == (z <=w)) or (x and w)
if f(x,y,z,w)==0:
print('x y z w')
print(x, y, z, w)
for l in product([0,1],repeat=4):
if f(l[0],l[1],l[2],l[3])==1:
print(*l)
13.
Решение14.
Проверкаfrom itertools import*
def f(z,y,x,w):
return ( (x <= y) == (z <=w)) or (x and w)
print(f(1,0,0,0))
print(f(1,1,0,0))
print(f(1,1,1,0))
15.
Программное решение16.
Программное решениеfrom itertools import*
def f(x,y,w,z):
return ( (x <= y) == (z <=w)) or (x and w)
for a1, a2, a3, a4,a5,a6 in product([0, 1], repeat=6):
t = [(1,a1,a2,a3),(1,1,a4,a5),(1,1,1,a6)]
if len(set(t)) != len(t):
continue
for p in permutations('xyzw'):
if [f(**dict(zip(p,r))) for r in t]==[0,0,0]:
print(*p, sep='')
17.
Программное решениеzyxw
18.
Задача 4Кодирование и декодирование
информации
Кодирование и
декодирование
информации
Расшифровка
сообщений
Кодирование и
декодирование
информации
Передача
информации. Выбор
кода
19.
Анализ. Все заглавные буквы русского алфавита
закодированы неравномерным двоичным
кодом, в котором никакое кодовое слово не
является началом другого кодового слова. Это
условие обеспечивает возможность
однозначной расшифровки закодированных
сообщений. Известны кодовые слова первых
букв алфавита: А — 001, Б — 011, В — 110.
Какую наименьшую длину может иметь код
слова ВОДОПРОВОД?
20.
АнализИзвестны кодовые слова первых букв алфавита:
А — 001, Б — 011, В — 110. Какую наименьшую
длину может иметь код слова ВОДОПРОВОД?
21.
АнализИзвестны кодовые слова первых букв алфавита:
А — 001, Б — 011, В — 110. Какую наименьшую
длину может иметь код слова ВОДОПРОВОД?
22.
АнализИзвестны кодовые слова первых букв алфавита:
А — 001, Б — 011, В — 110. Какую наименьшую
длину может иметь код слова ВОДОПРОВОД?
23.
АнализИзвестны кодовые слова первых букв алфавита:
А — 001, Б — 011, В — 110. Какую наименьшую
длину может иметь код слова ВОДОПРОВОД?
24.
Задача 6Определение результатов работы
исполнителей
25.
ЗадачаИсполнитель Черепаха передвигается по плоскости и оставляет
след в виде линии.
В начальный момент Черепаха находится в начале координат и
направлена вверх (вдоль положительного направления оси
ординат), хвост опущен.
Черепахе был дан для исполнения следующий алгоритм:
Направо 315
Повтори 7 [Вперёд 16 Направо 45 Вперёд 8 Направо 135]
Определите, сколько точек с целочисленными координатами
будет находиться внутри фигуры, ограниченной заданным
алгоритмом линиями, не включая точки на линиях.
26.
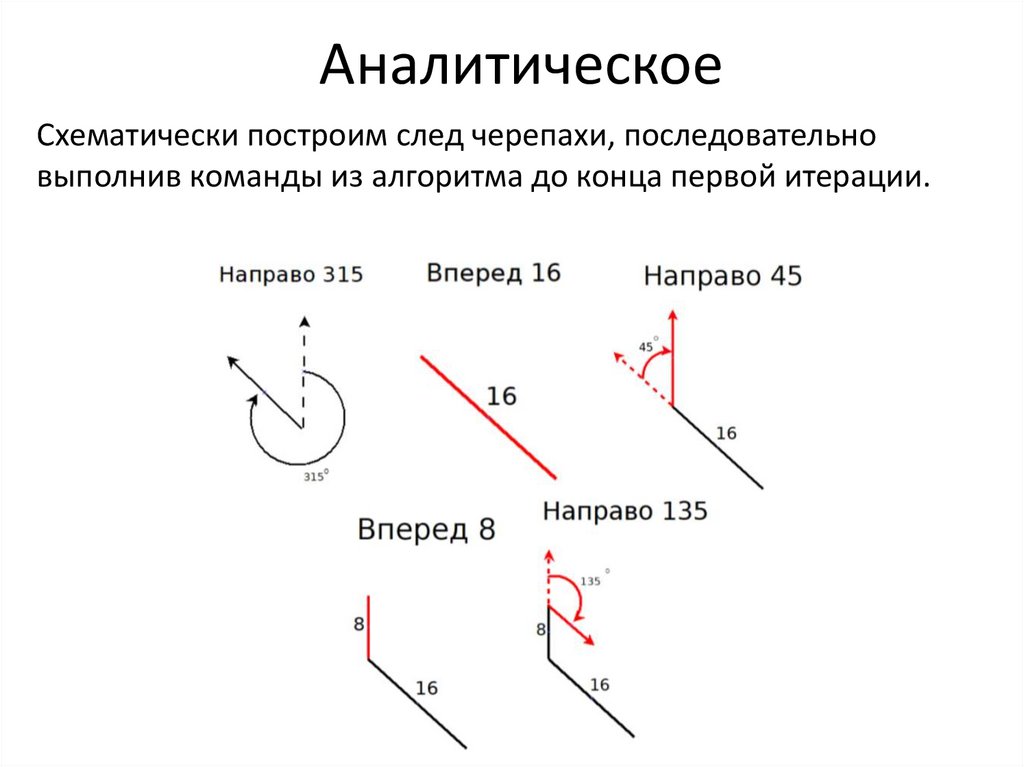
АналитическоеСхематически построим след черепахи, последовательно
выполнив команды из алгоритма до конца первой итерации.
27.
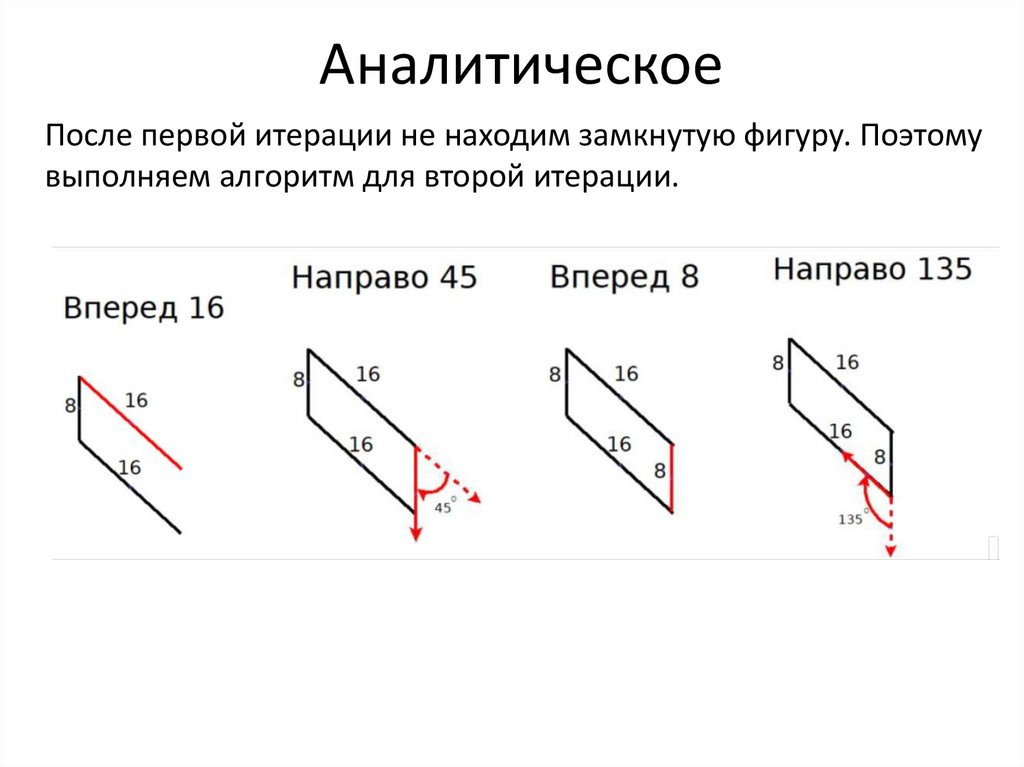
АналитическоеПосле первой итерации не находим замкнутую фигуру. Поэтому
выполняем алгоритм для второй итерации.
28.
АналитическоеЗаметим, что исполнитель вернулся в точку, отеуда началась
первая итерация. Следовательно, остальные 5 итераций будут
просто повторять рисунок поверх уже нарисованного следа.
При выполнении алгоритма стоит помнить текущие углы
отклонения. Так, например, после первой команды
исполнитель будет отклонен от оси оХ на 45 градусов, при
следующем повороте отклонение будет на 90 градусов и т.д.
Так же из курса геометрии мы знаем, что линия, проведенная
под углом 45 градусов, начинающаяся в точке (x, y) с
целочисленными координатами, проходит через все точки с
кординатами (x+k, y+k), где k – целое число.
29.
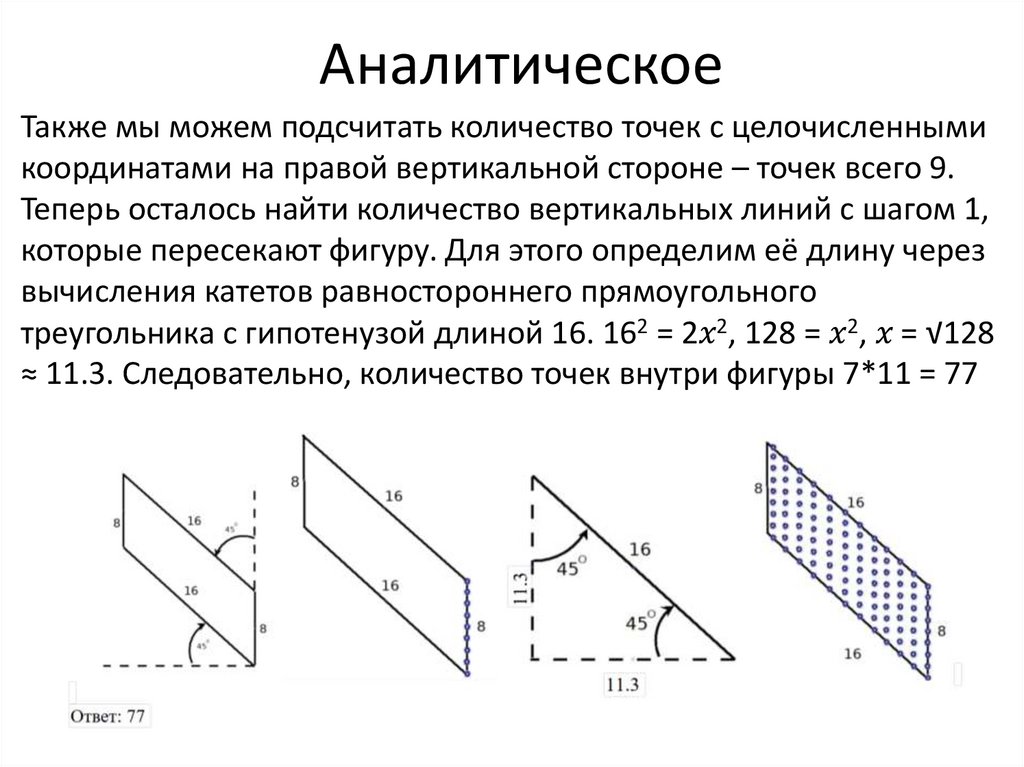
АналитическоеТакже мы можем подсчитать количество точек с целочисленными
координатами на правой вертикальной стороне – точек всего 9.
Теперь осталось найти количество вертикальных линий с шагом 1,
которые пересекают фигуру. Для этого определим её длину через
вычисления катетов равностороннего прямоугольного
треугольника с гипотенузой длиной 16. 162 = 2




























































 programming
programming








