Целые, рациональные и иррациональные числа. Делимость чисел. Корень степени n. Арифметический корень

1.

Целые, рациональные и иррациональные числа.
Делимость чисел. Корень степени n. Арифметический корень
§ 1. Целые, рациональные и иррациональные числа.
1.1 Множество целых чисел
Необходимость рассмотрения целых чисел
продиктована невозможностью (в общем случае)
вычесть из одного натурального числа другое.
Если определено положение натуральных чисел на
координатной прямой и число 0, мы можем расширить
числовое множество так, чтобы операция вычитания
была определена на всем множестве.

2.

Целые, рациональные и иррациональные числа.
Делимость чисел. Корень степени n. Арифметический корень
Определения:
1. Множество всех чисел, противоположных
натуральным, называется множеством
целых отрицательных чисел.
2. Сами натуральные числа при этом называют
целыми положительными числами.
3. Множество целых отрицательных чисел, множество
целых положительных чисел и число нуль вместе
называются множеством целых чисел.

3.

Целые, рациональные и иррациональные числа.
Делимость чисел. Корень степени n. Арифметический корень
Множество целых чисел
определяется как замыкание множества натуральных
чисел N относительно арифметических операций
сложения (+) и вычитания (–).
Таким образом, сумма, разность и произведение
двух целых чисел есть снова целые числа.
Целые числа являются кольцом относительно
операций сложения и умножения.

4.

Целые, рациональные и иррациональные числа.
Делимость чисел. Корень степени n. Арифметический корень
Множество целых чисел состоит из:
• натуральных чисел n (1, 2, 3, …),
• чисел вида -n (nϵ N)
• числа нуль

5.

Целые, рациональные и иррациональные числа.
Делимость чисел. Корень степени n. Арифметический корень
Отрицательные числа в математический обиход
ввели :
немецкий математик Михаэль Штифель (1487—1567)
в книге «Полная арифметика» (1544),
и французский математик Никола Шюке (1445—1500).

6.

Целые, рациональные и иррациональные числа.
Делимость чисел. Корень степени n. Арифметический корень
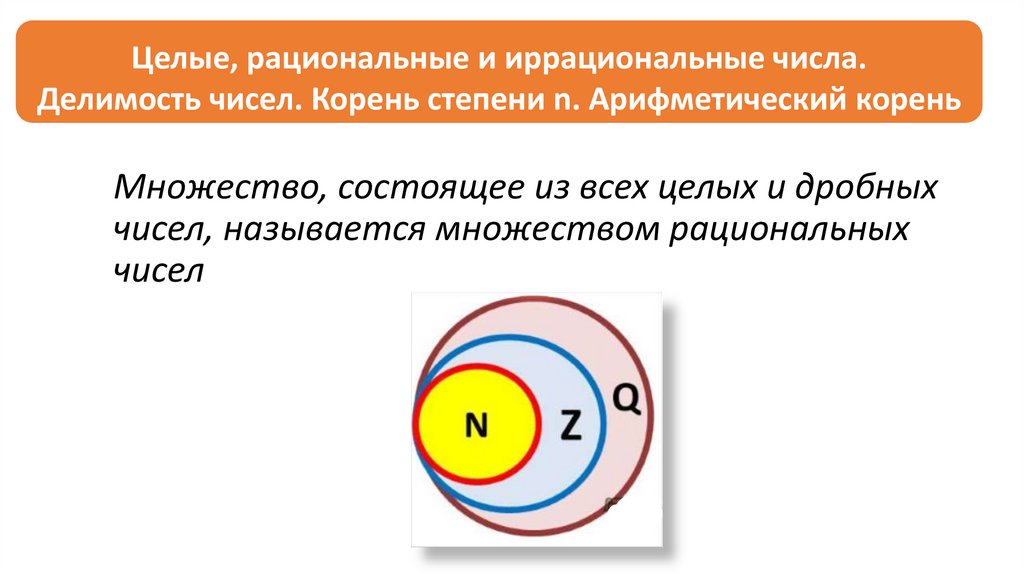
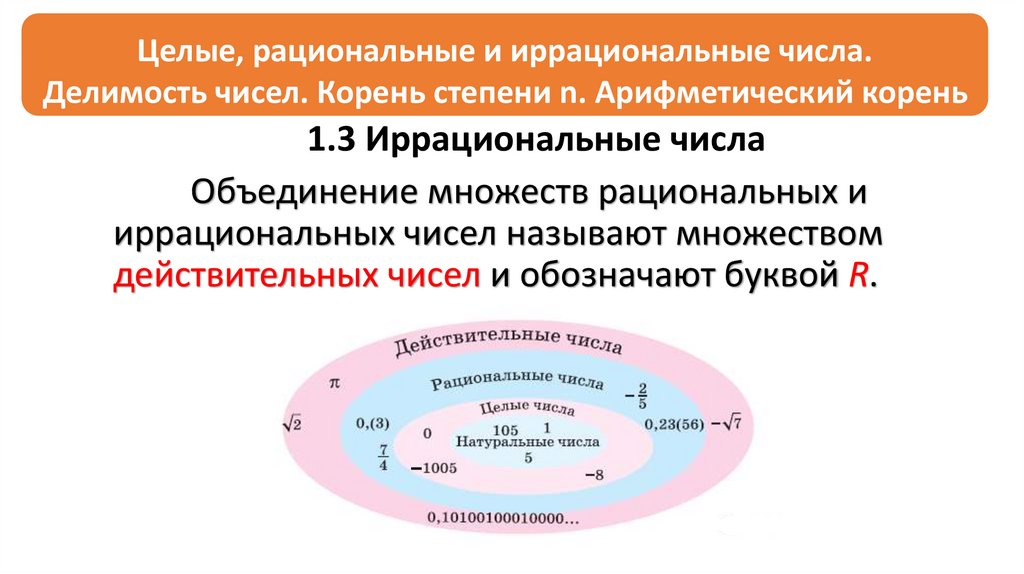
1.2 Множество рациональных чисел
Необходимость рассмотрения новых чисел
продиктована невозможностью (в общем случае)
разделить одно целое число на другое.
Вводятся так называемые дробные положительные
числа:
1 1 3 8
, , ,
2 8 5 7
Вводятся так называемые дробные отрицательные числа
(противоположные дробным положительным):
1
1 3 8
- , - ,- ,2
8
5
7

7.

Целые, рациональные и иррациональные числа.
Делимость чисел. Корень степени n. Арифметический корень
1.2 Множество рациональных чисел
Определение. Рациональным (лат. ratio —
отношение, деление, дробь) называется всякое