Целые числа. Рациональные числа

1. Целые числа Рациональные числа

МАТЕМАТИКА
6р класс
27 января 2022 г.

2. ЗАДАНИЕ

Начертите координатную прямую, приняв за единичный отрезок 1 клетку
тетради. Отметьте на координатной прямой точки:
М (0)
А (-3)
В (2)
С(5)
D (3)
E (-1,5)

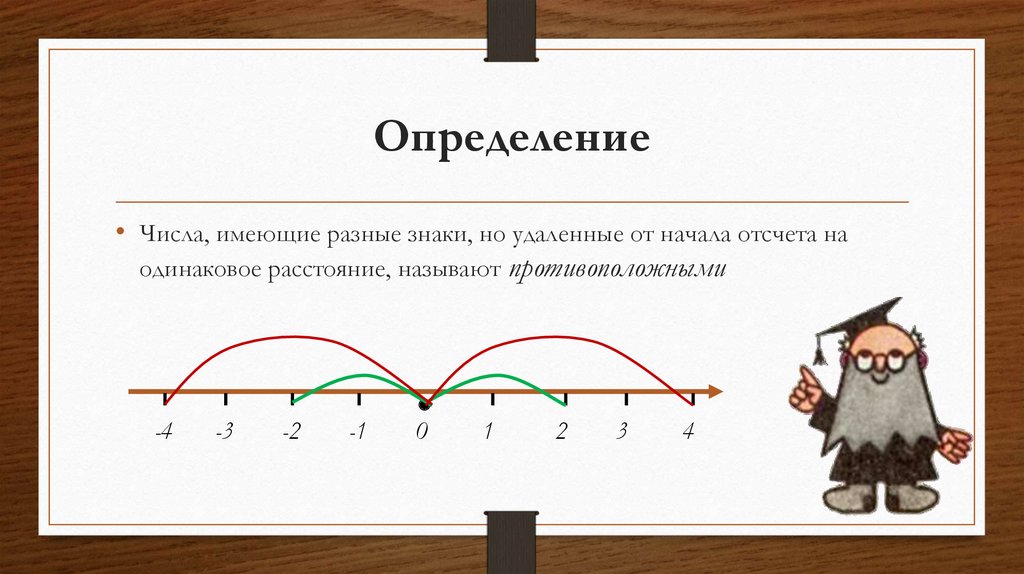
3. Определение

• Числа, имеющие разные знаки, но удаленные от начала отсчета на
одинаковое расстояние, называют противоположными
-4
-3
-2
-1
0
1
2
3
4

4. ЗАДАНИЕ

• Найти и отметить на координатной прямой противоположные данным
числа:
М (0)
А (-3)
В (2)
С(5)
D (3)
E (-1,5)

5.

Для каждого числа есть только одно
противоположное ему число
Знаки «+» и «-» называются
противоположными знаками
Число, противоположное положительному числу,
есть число отрицательное
Число, противоположное отрицательному числу.
есть число положительное
Число 0 противоположно самому себе

6. ПРАВИЛО

• Приписав противоположный знак к данному числу, получаем число,
противоположное данному
а и –а
-(-а) = а
-Запись скобок обязательна!

7. Правила знаков

Если перед скобкой стоит знак «+»,
то при записи без скобок знаки чисел сохраняются
+(+6)=+6
+(-7)=-7
Если перед скобкой стоит знак «-»,
то при записи без скобок знак числа меняется на противоположный
-(+4) = -4
-(-9)=+9

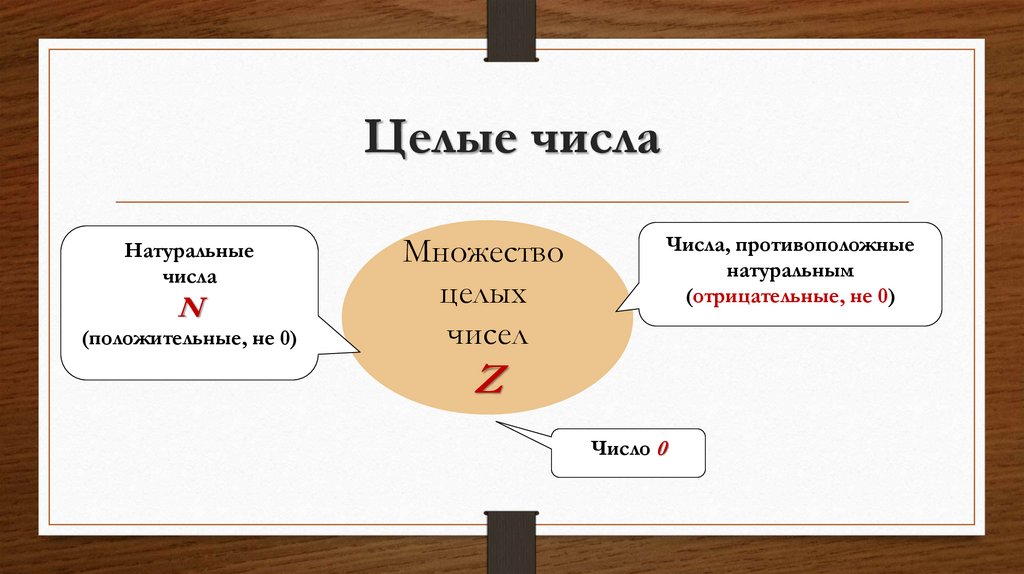
8. Целые числа

Натуральные
числа
N
(положительные, не 0)
Множество
целых
чисел
Числа, противоположные
натуральным
(отрицательные, не 0)
Z
Число 0

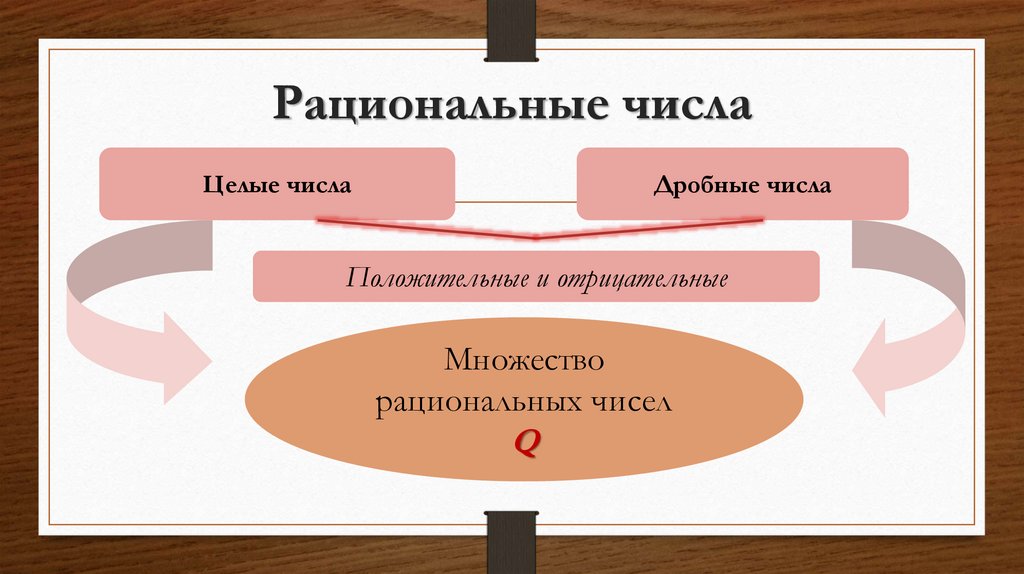
9. Рациональные числа

Целые числа
Дробные числа
Положительные и отрицательные
Множество
рациональных чисел
Q

10.

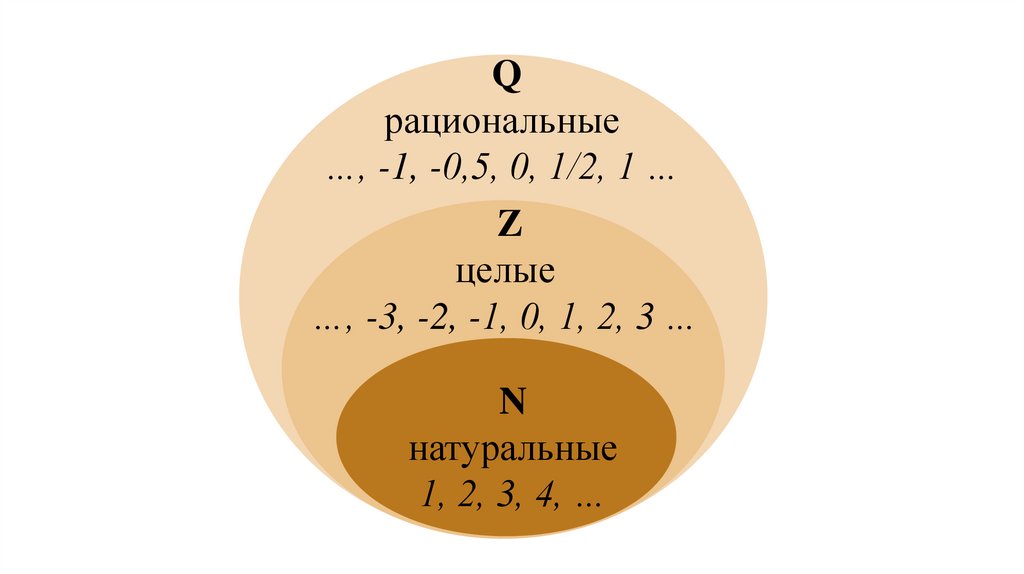
Q
рациональные
…, -1, -0,5, 0, 1/2, 1 …
Z
целые
…, -3, -2, -1, 0, 1, 2, 3 …
N
натуральные
1, 2, 3, 4, …

11. Множества. Числовые множества.

12.

Наборы объектов, объединённых общим
для каждого набора свойством
называют множествами
«Множество учеников класса»
«Множество делителей числа 6»
«Множество точек плоскости,
удалённых от точки О на 2см»

13.

В математике термин «множество» не имеет
количественного смысла.
Множество делителей числа 1 состоит из одного
элемента – числа 1 – это множество конечное.
Множество общих кратных чисел 2 и 3 является
бесконечным – 6, 12, 18, 24, ….

14.

В математике встречаются множества, в которых нет ни одного
элемента, например множество чисел, делящихся на нуль.
Такое множество называют пустым.
Ø – пустое множество

15.

Числа 1, 2, 3, 4, 6, 12 – являются элементами множества делителей числа 12
«1, 2, 3, 4, 6, 12 – принадлежат ( ) множеству делителей
числа 12»
«5, 7 – не принадлежат( ) множеству делителей числа 12»

16.

А – множество делителей числа 12 (1, 2, 3 ,4, 6, 12)
В – множество делителей числа 18 (1, 2, 3 , 6, 9, 18)

17.

Множество А называют подмножеством множества В,
если каждый элемент множества А
принадлежит множеству В
A B
A
B

18.

B – множество делителей числа 12
(1, 2, 3 ,4, 6, 12)
A – множество делителей числа 6
(1, 2, 3 , 6)
A B

19.

Два множества равны, если они состоят
из одних и тех же элементов
или вообще не содержат элементов.