Similar presentations:
Граф, вершина, ребро. Представление задачи с помощью графа
1.
Граф, вершина, ребро.Представление задачи с
помощью графа
2.
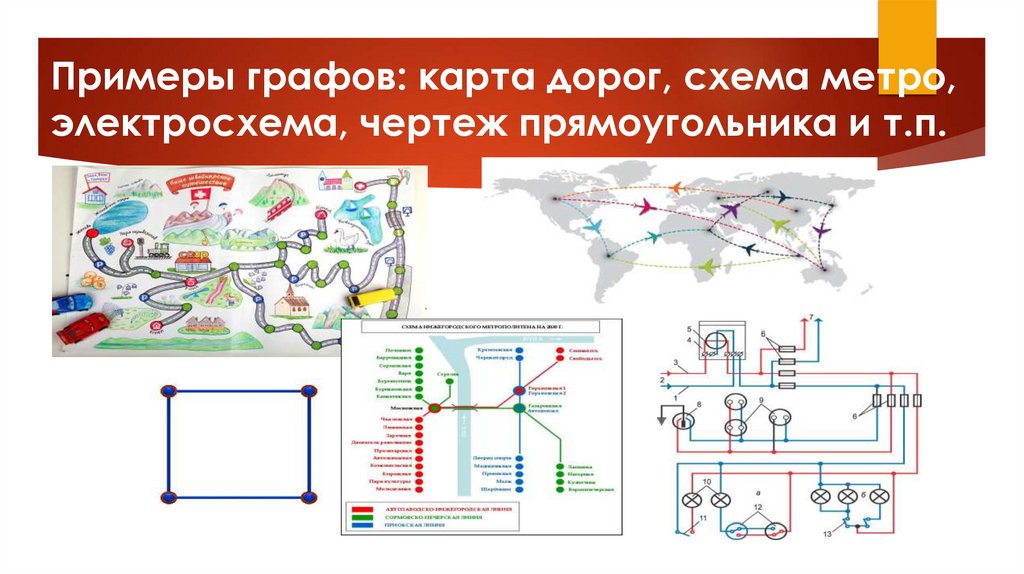
Примеры графов: карта дорог, схема метро,электросхема, чертеж прямоугольника и т.п.
3.
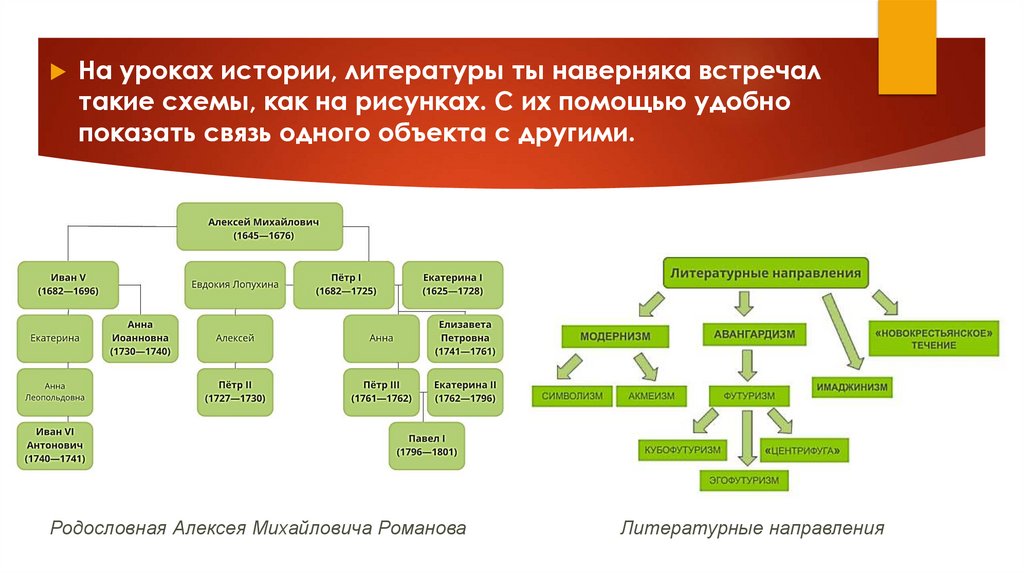
На уроках истории, литературы ты наверняка встречалтакие схемы, как на рисунках. С их помощью удобно
показать связь одного объекта с другими.
Родословная Алексея Михайловича Романова
Литературные направления
4.
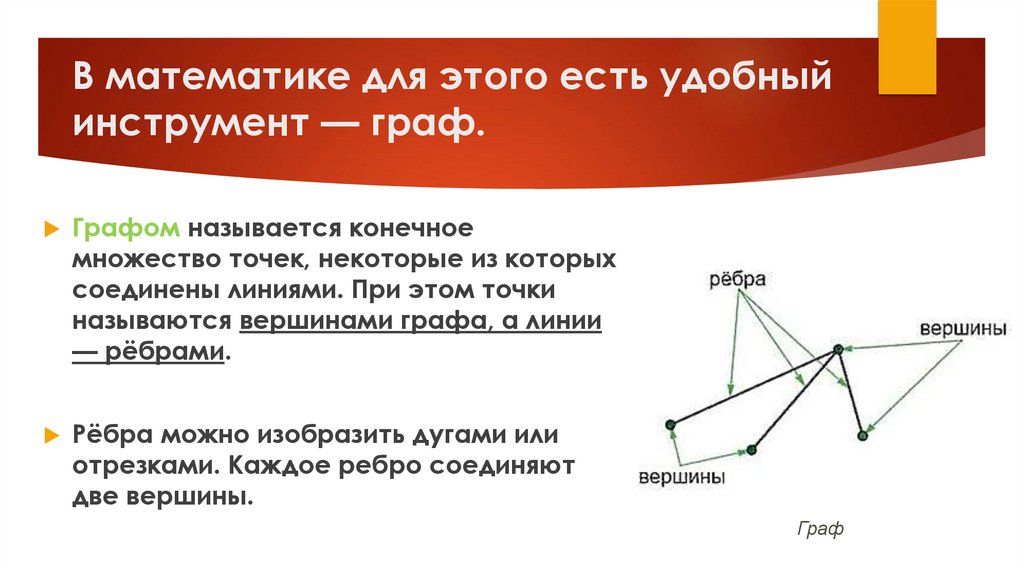
В математике для этого есть удобныйинструмент — граф.
Графом называется конечное
множество точек, некоторые из которых
соединены линиями. При этом точки
называются вершинами графа, а линии
— рёбрами.
Рёбра можно изобразить дугами или
отрезками. Каждое ребро соединяют
две вершины.
Граф
5.
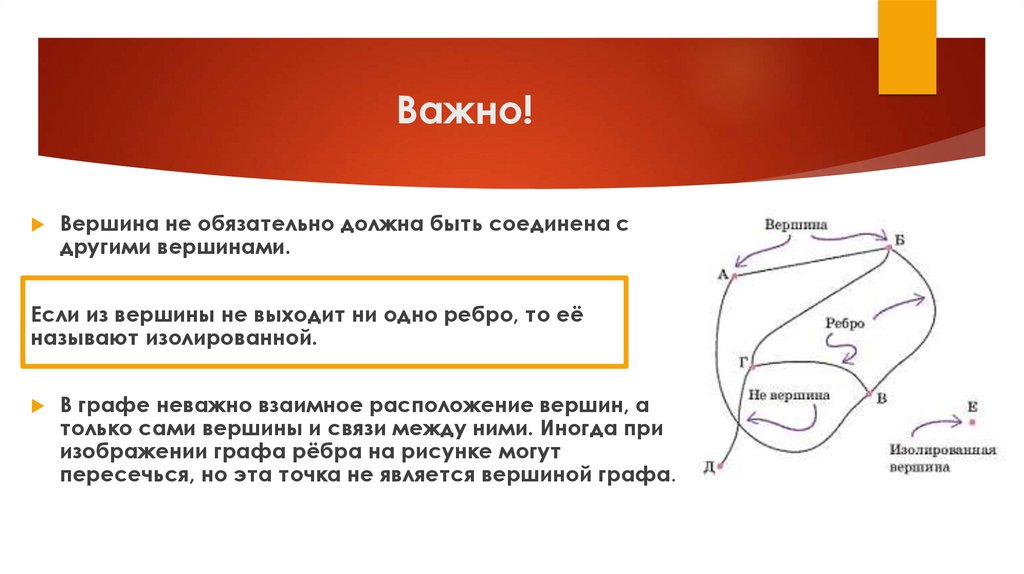
Важно!Вершина не обязательно должна быть соединена с
другими вершинами.
Если из вершины не выходит ни одно ребро, то её
называют изолированной.
В графе неважно взаимное расположение вершин, а
только сами вершины и связи между ними. Иногда при
изображении графа рёбра на рисунке могут
пересечься, но эта точка не является вершиной графа.
6.
Важно!Степенью (или порядком) вершины называется количество рёбер, которые
выходят из этой вершины.
Пример: на рисунке 1 степень вершины А равна 2, степень вершины В — 4,
С, D, E, F — 1.
Найдём сумму степеней всех вершин.
2+4+1+1+1+1=10.
Посчитаем по рисунку количество рёбер, оно равно 5.
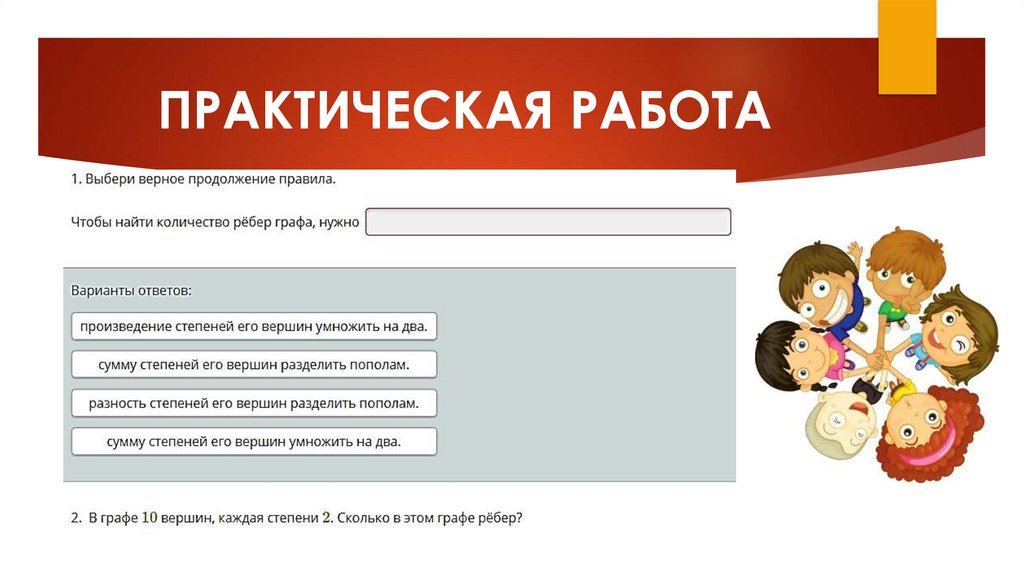
Чтобы найти количество рёбер, нужно сумму степеней его вершин
разделить пополам.
7.
ПРАКТИЧЕСКАЯ РАБОТА№1.
8.
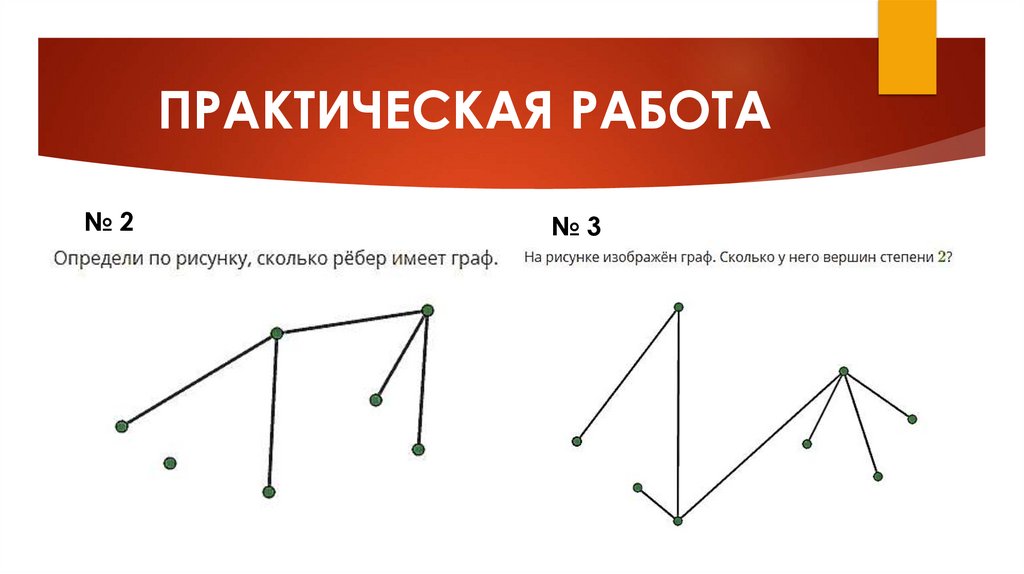
ПРАКТИЧЕСКАЯ РАБОТА№2
№3
9.
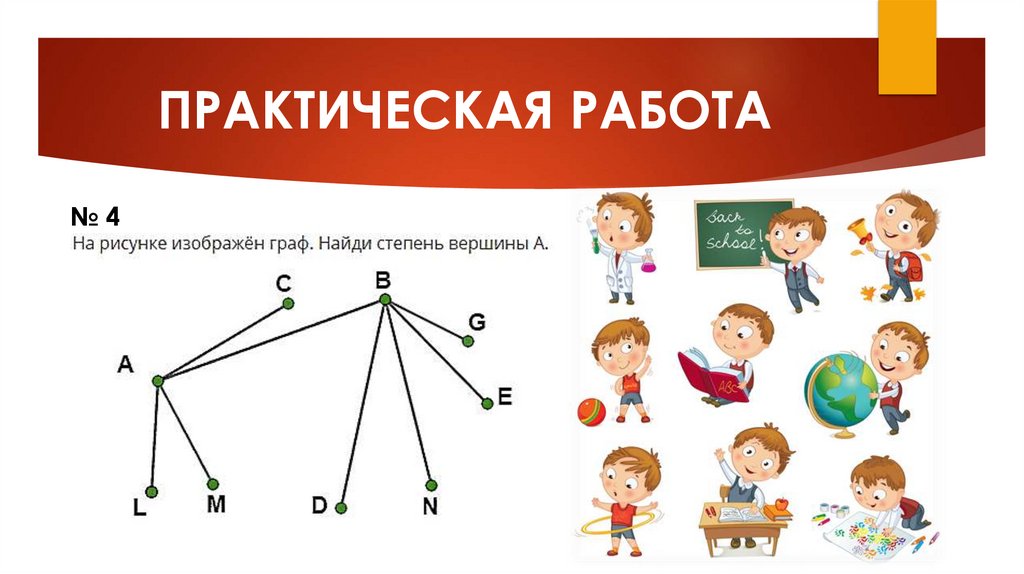
ПРАКТИЧЕСКАЯ РАБОТА№4
10.
ПРАКТИЧЕСКАЯ РАБОТА№5
11.
ПРАКТИЧЕСКАЯ РАБОТА12.
ПРАКТИЧЕСКАЯ РАБОТА№7
№8
№9
№ 10





 programming
programming








