Закон Бернулли

1.

Закон Бернулли

2.

Дании́л Берну́лли (Daniel
Bernoulli; 29 января (8
февраля) 1700 — 17 марта
1782), швейцарский физикуниверсал, механик и
математик, один из создателей
кинетической теории газов,
гидродинамики и
математической физики.
Академик и иностранный
почётный член (1733)
Петербургской академии наук,
член Академий: Болонской
(1724), Берлинской (1747),
Парижской (1748),
Лондонского королевского
общества (1750). Сын Иоганна
Бернулли.

3.

Как известно, неподвижная жидкость в сосуде, согласно закону Паскаля,
передает внешнее давление ко всем точкам жидкости без изменения. Но
когда
жидкость течет без трения по трубе переменной толщины, давление в
разных
местах трубы неодинаково. Оказывается, в узких местах трубы давление
жидкости меньше, чем в широких.
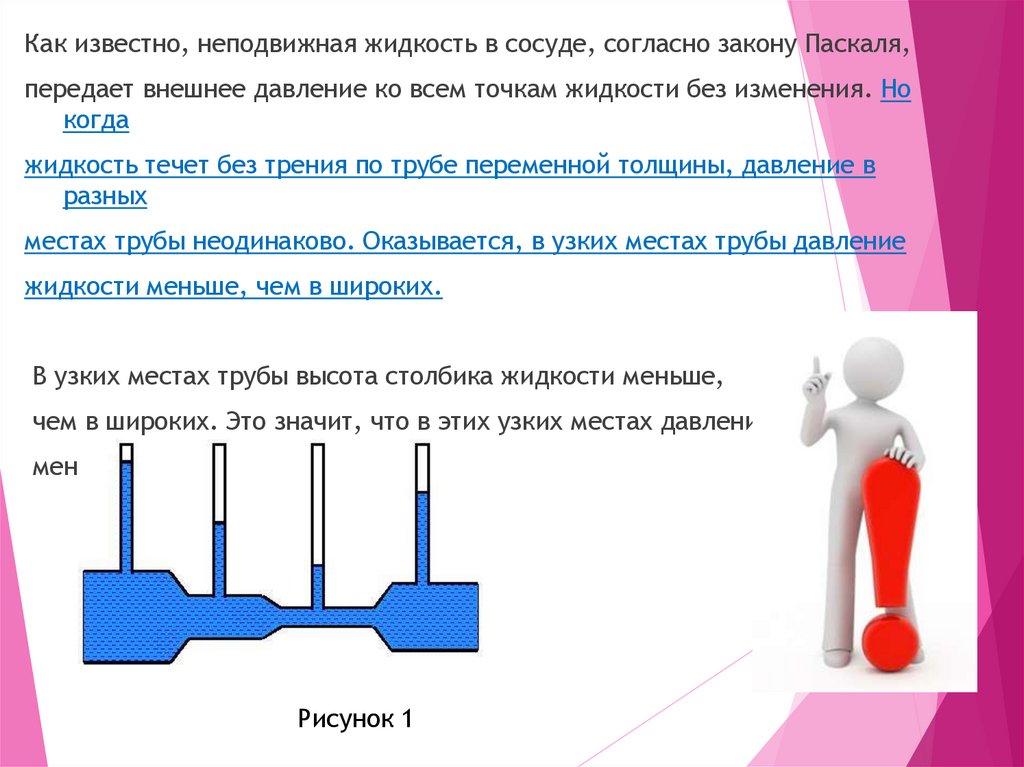
В узких местах трубы высота столбика жидкости меньше,
чем в широких. Это значит, что в этих узких местах давление
меньше. Смотри рисунок 1
Рисунок 1

4.

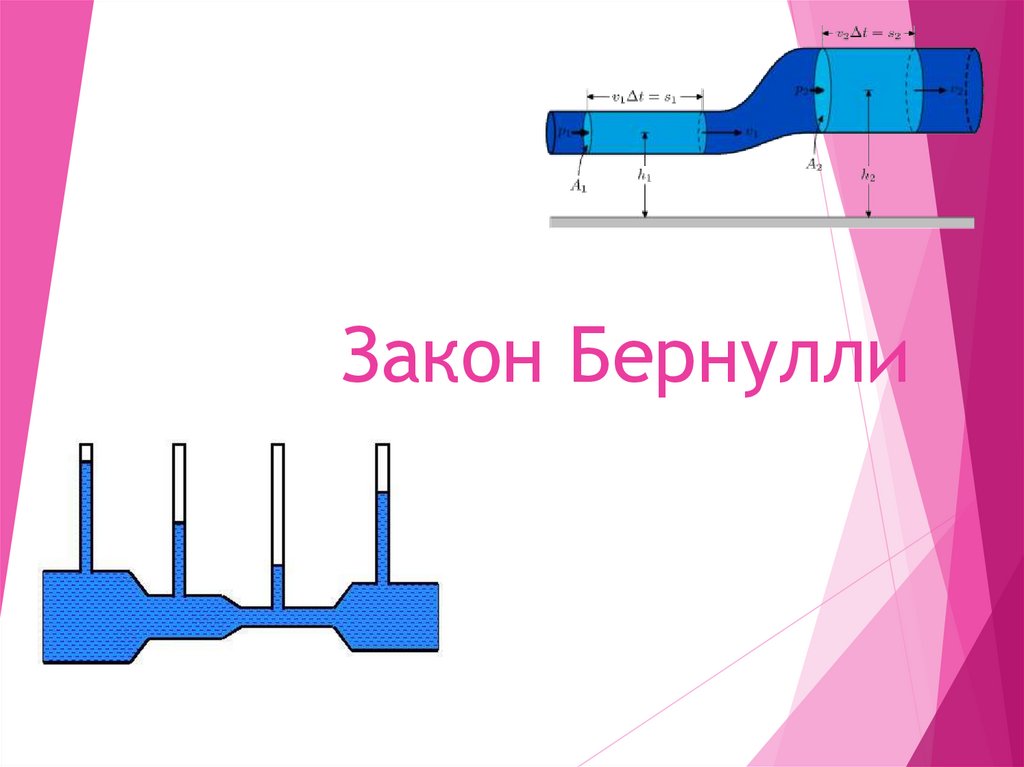
Скорость жидкости и сечение трубы.
Предположим, что жидкость течет по горизонтальной трубе,
сечение которой в разных местах различное. Выделим
мысленно несколько сечений в трубе, площади которых
обозначим S1, S2, S3. За какой-то промежуток времени t через
каждое из этих сечений должна пройти жидкость одного и
того же объема. Вся жидкость, которая за время t походит
через первое сечение, должна за это же время пройти второе
сечение и третье сечение. Заметим, что мы считаем, что
жидкость данной массы повсюду имеет один объем, что она
не может сжиматься (несжимаема).
Но как жидкость, протекающая
через первое сечение, может
«успеть» за то же время
протечь через значительно
меньшее сечение S2? Очевидно,
что для этого при прохождении
узких частей трубы скорость
движения жидкости должна
быть больше, чем при

5.

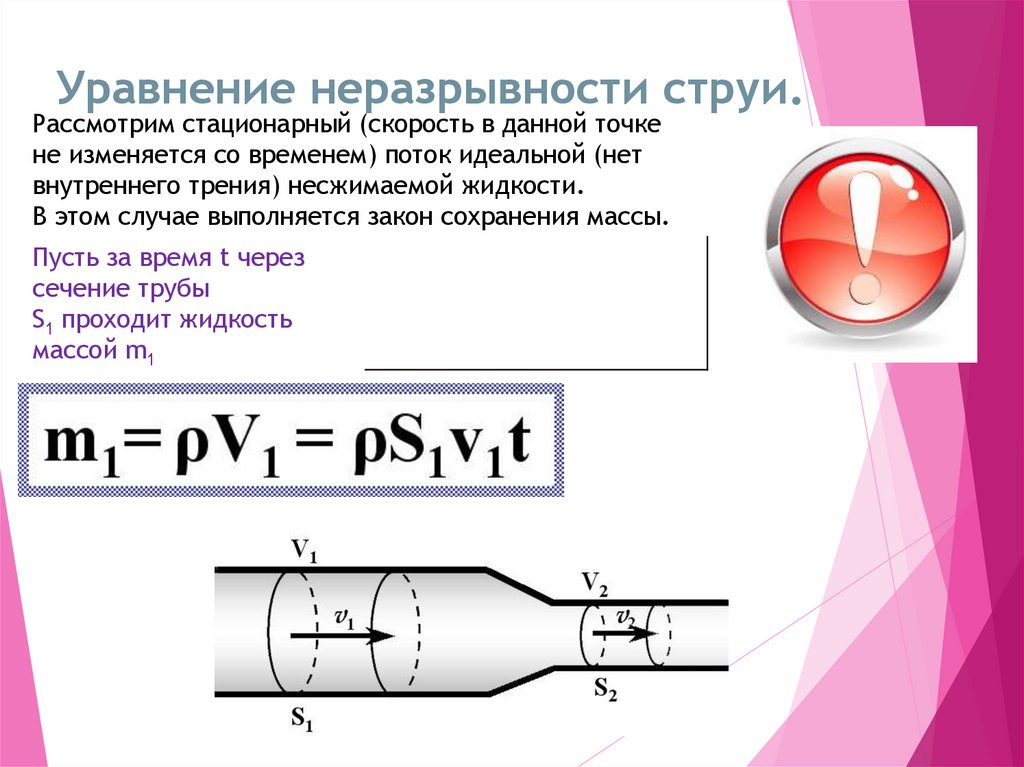
Уравнение неразрывности струи.
Рассмотрим стационарный (скорость в данной точке
не изменяется со временем) поток идеальной (нет
внутреннего трения) несжимаемой жидкости.
В этом случае выполняется закон сохранения массы.
Пусть за время t через
сечение трубы
S1 проходит жидкость
массой m1

6.

Тогда через сечение S2 за тоже время проходит
жидкость массой m2:
Так как m1=m2,
то
или
Где сечение трубы меньше, там скорость
жидкости больше, и наоборот (если S1 > S2, то
v1 < v2).

7.

Скорость и давление.
Так как при переходе жидкости из широкого участка в узкий скорость
течения увеличивается, то это значит, что где-то на границе между
узким и широким участком трубы жидкость получает ускорение. А по
второму закону Ньютона для этого на этой границе должна действовать
сила. Этой силой может быть только разность между силами давления
в широком и узком участках трубы. В широком участке трубы давление
должно быть больше, чем в узком. Этот вывод следует из закона
сохранения энергии.
Если в узких местах трубы увеличивается скорость жидкости, то
увеличивается и ее кинетическая энергия

8.

А так как мы условились, что жидкость течет без трения,
то этот прирост кинетической энергии должен
компенсироваться уменьшением потенциальной энергии,
потому что полная энергия должна оставаться
постоянной.
Но это не потенциальная энергия mgh, потому что труба
горизонтальная и высота h везде одинакова. Значит,
остается только потенциальная энергия, связанная с
силой упругости. Сила давления жидкости – это и есть
сила упругости сжатой жидкости. В широкой части трубы
жидкость несколько сильнее сжата, чем в узкой. Правда,
мы только что говорили, что жидкость считается
несжимаемой. Но это значит, что жидкость не настолько
сжата, чтобы сколько-нибудь заметно изменился ее
объем.

9.

Очень малое сжатие, вызывающее появление силы
упругости, неизбежно. Оно и уменьшается в узких
частях трубы.
В этом и состоит закон (принцип), открытый в 1738 г.
петербургским академиком Даниилом Бернулли:
Давление в жидкости, текущей в трубе,
больше в тех частях, где скорость ее
движения меньше, и наоборот, в тех частях,
где скорость больше, давление меньше.

10.

Закон Бернулли относится не только
к жидкости, но и к газу, если газ не
сжимается на столько, чтобы
изменился его объем. В узких частях
труб скорость течения жидкости
велика, а давление мало. Можно
подобрать такое маленькое сечение
трубы, что давление в потоке будет
меньше атмосферного.

11.

Уравнение Д.Бернулли:

12.

Если взять полоску бумаги и дуть вдоль ее
поверхности, то полоска поднимется вверх.
Давление газа над полоской меньше давления снизу.

13.

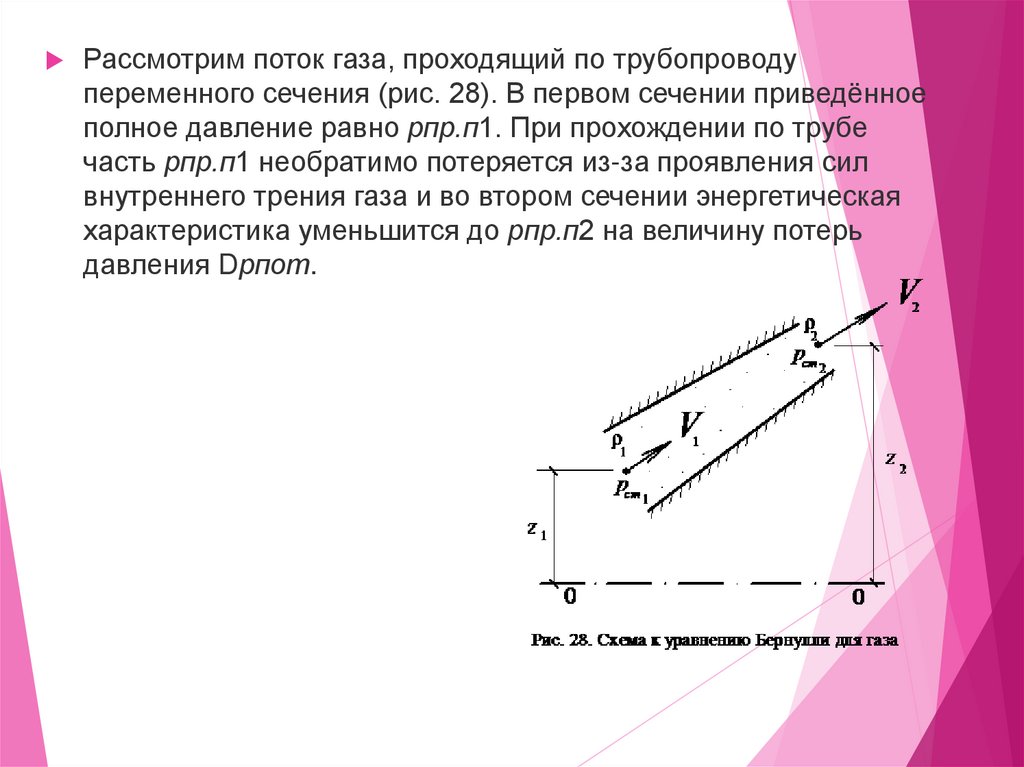
Рассмотрим поток газа, проходящий по трубопроводу
переменного сечения (рис. 28). В первом сечении приведённое
полное давление равно pпр.п1. При прохождении по трубе
часть pпр.п1 необратимо потеряется из-за проявления сил
внутреннего трения газа и во втором сечении энергетическая
характеристика уменьшится до pпр.п2 на величину потерь
давления Dpпот.

14.

Энергетический смысл уравнения
Бeрнýлли
для газа заключается в том, что оно отражает
закон
сохранения
энергии,
а
геометрический не рассматривается, так как
величины в нём выражаются в единицах
давления (Па), а не напора (м). Движение
газа происходит только при наличии разности
приведённых полных давлений Dpпр = pпр.п1
– pпр.п2 от бóльшего давленияpпр.п1 к
меньшему pпр.п2. Например, так работает
естественная вентиляция для удаления
воздуха из помещений зданий.

15.

Потери
давления Dpпот отражают потерю
полной энергии потока при движении газа.
Например, чем длиннее воздуховод, меньше его
проходное сечение, шероховатее его стенки, тем
больше будут потери давления Dpпот в системе
вентиляции, что может ухудшить удаление
несвежего воздуха из помещений.
При установившемся движении газа разность
давлений численно равна потерям давления:
Dpпр = Dpпот .
Таким образом, «разность давлений» является
причиной движения газа, а «потери давления» —
следствием. Измеряются они в одних и тех же
единицах СИ — паскалях (Па).

16.

Спасибо за внимание!!