Угол между прямыми. Угол между прямой и плоскостью. Геометрия, 10 класс

1.

Угол между прямыми. Угол между
прямой и плоскостью.
Геометрия, 10 класс.
Воробьев Леонид Альбертович, г.Минск

2.

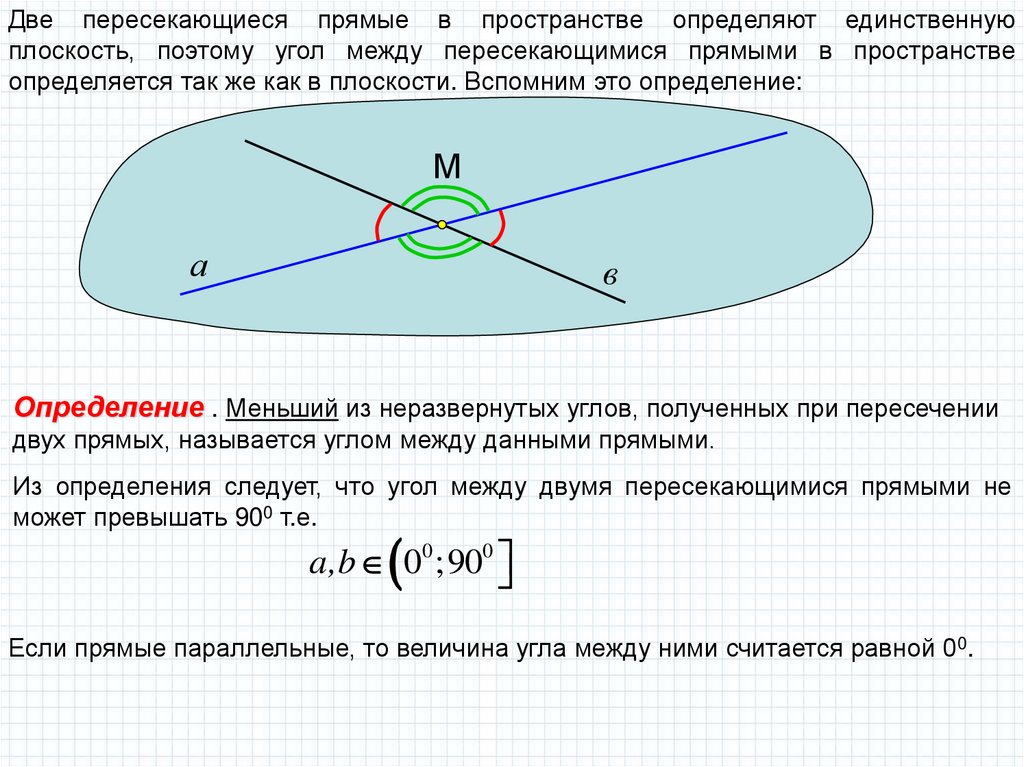
Две пересекающиеся прямые в пространстве определяют единственную
плоскость, поэтому угол между пересекающимися прямыми в пространстве
определяется так же как в плоскости. Вспомним это определение:
М
а
в
Определение . Меньший из неразвернутых углов, полученных при пересечении
двух прямых, называется углом между данными прямыми.
Из определения следует, что угол между двумя пересекающимися прямыми не
может превышать 900 т.е.
a,b 00 ;900
Если прямые параллельные, то величина угла между ними считается равной 00.

3.

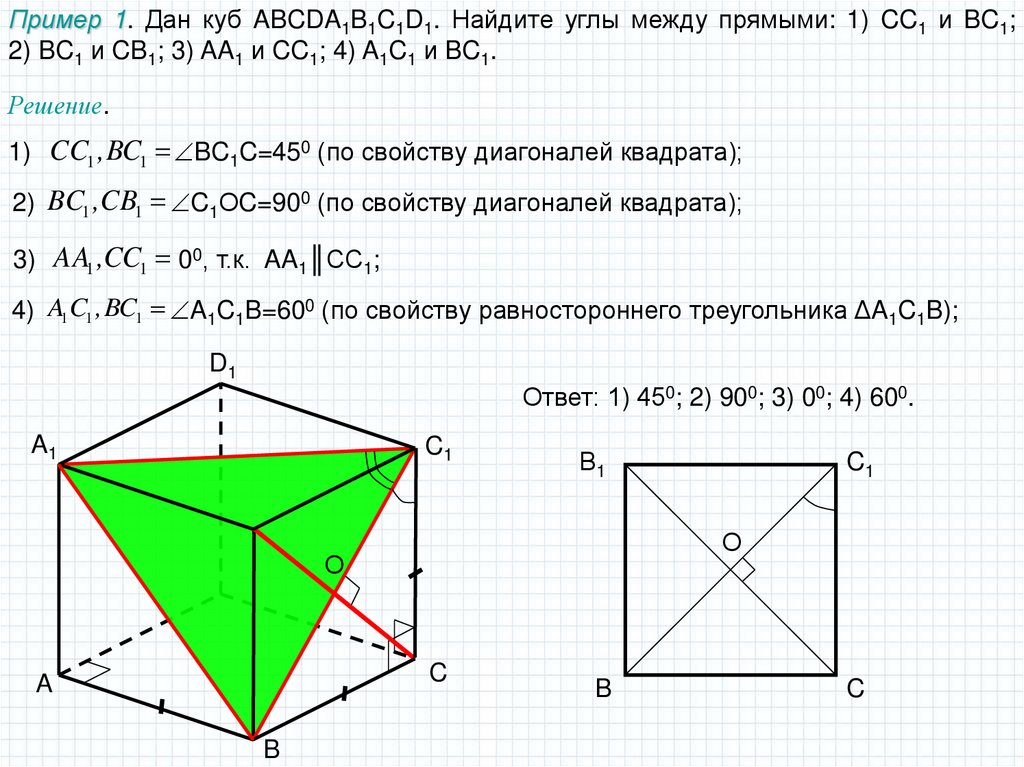
Пример 1. Дан куб ABCDA1B1C1D1. Найдите углы между прямыми: 1) CC1 и BC1;
2) BC1 и CB1; 3) AA1 и CC1; 4) A1C1 и BC1.
Решение.
1) CC1 ,BC1 BC1C=450 (по свойству диагоналей квадрата);
2) BC1 ,CB1 C1ОC=900 (по свойству диагоналей квадрата);
3) AA1 ,CC1 00, т.к. AA1║CC1;
4) A1 C1 ,BC1 A1C1B=600 (по свойству равностороннего треугольника ΔA1C1B);
D1
Ответ: 1) 450; 2) 900; 3) 00; 4) 600.
A1
C1
В1
О
О
C
A
B
C1
B
C

4.

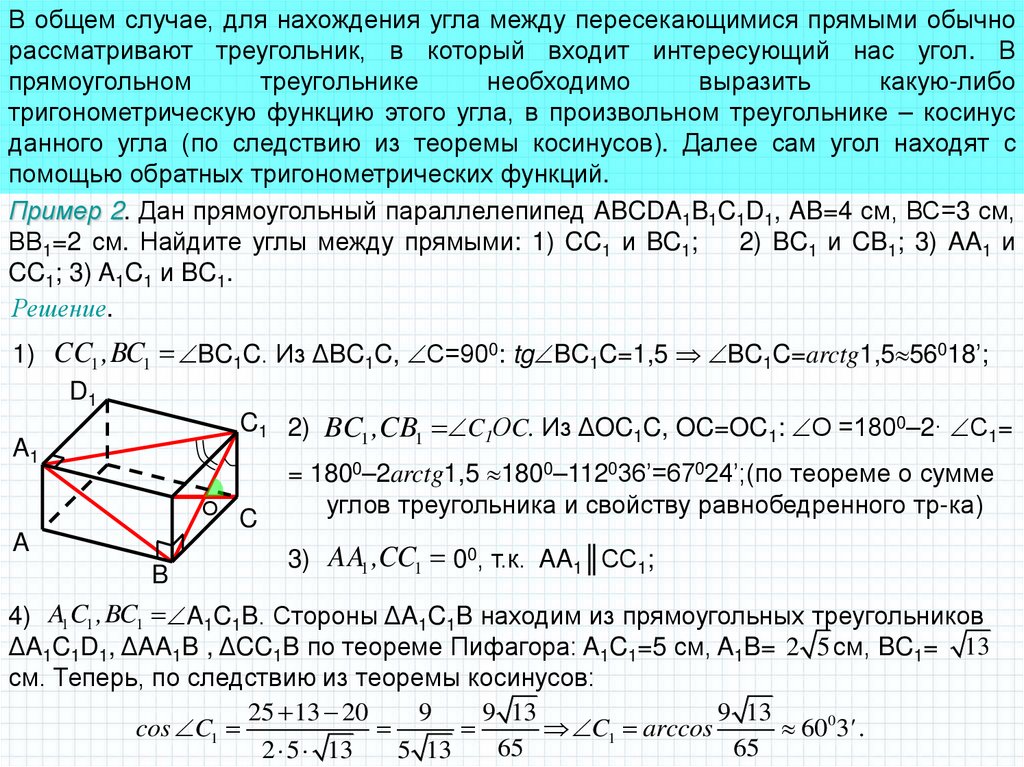
В общем случае, для нахождения угла между пересекающимися прямыми обычно
рассматривают треугольник, в который входит интересующий нас угол. В
прямоугольном
треугольнике
необходимо
выразить
какую-либо
тригонометрическую функцию этого угла, в произвольном треугольнике – косинус
данного угла (по следствию из теоремы косинусов). Далее сам угол находят с
помощью обратных тригонометрических функций.
Пример 2. Дан прямоугольный параллелепипед ABCDA1B1C1D1, AB=4 см, ВС=3 см,
ВВ1=2 см. Найдите углы между прямыми: 1) CC1 и BC1;
2) BC1 и CB1; 3) AA1 и
CC1; 3) A1C1 и BC1.
Решение.
1) CC1 ,BC1 BC1C. Из ΔBC1C, С=900: tg BC1C=1,5 BC1C=arctg1,5 56018’;
D1
C1 2) BC ,CB C1ОC. Из ΔOC1C, OC=OC1: О =1800–2· С1=
1
1
A1
= 1800–2arctg1,5 1800–112036’=67024’;(по теореме о сумме
углов треугольника и свойству равнобедренного тр-ка)
О
C
A
3) AA1 ,CC1 00, т.к. AA1║CC1;
B
4) A1 C1 ,BC1 A1C1B. Стороны ΔA1C1B находим из прямоугольных треугольников
ΔA1C1D1, ΔAA1B , ΔCC1B по теореме Пифагора: A1C1=5 см, A1B= 2 5 см, BC1= 13
см. Теперь, по следствию из теоремы косинусов:
25 13 20
9
9 13
9 13
cos C1
C1 arccos
6003' .
65
65
2 5 13
5 13

5.

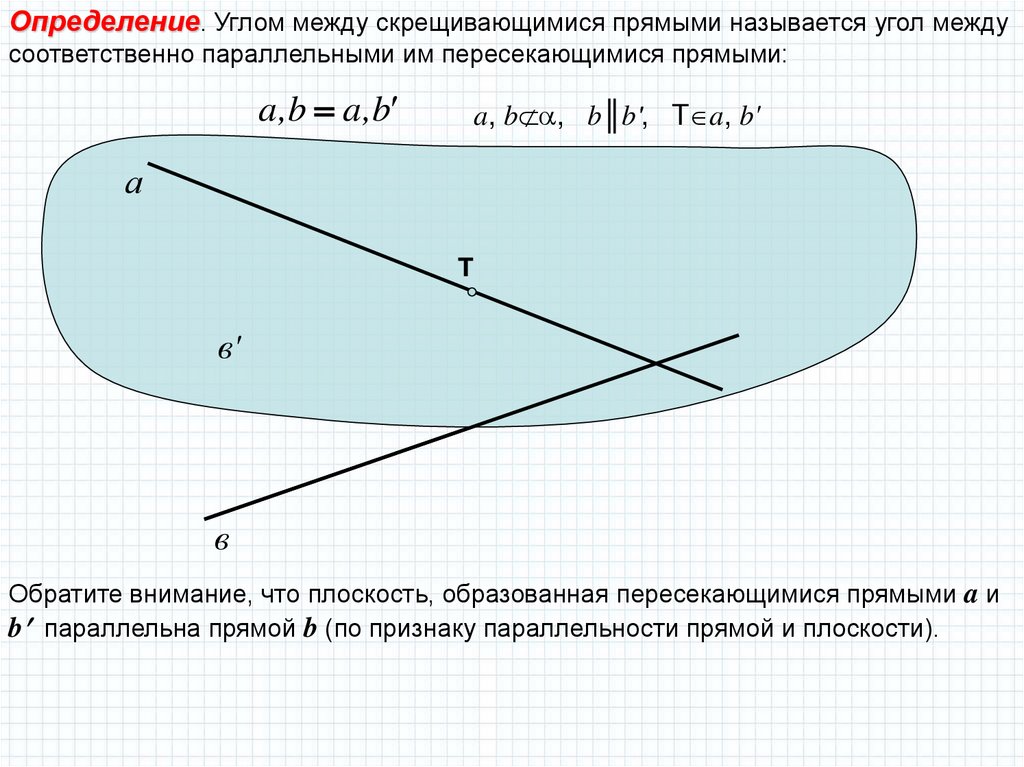
Определение. Углом между скрещивающимися прямыми называется угол между
соответственно параллельными им пересекающимися прямыми:
a,b a,b
a, b , b║b', T a, b'
а
T
в'
в
Обратите внимание, что плоскость, образованная пересекающимися прямыми a и
b параллельна прямой b (по признаку параллельности прямой и плоскости).

6.

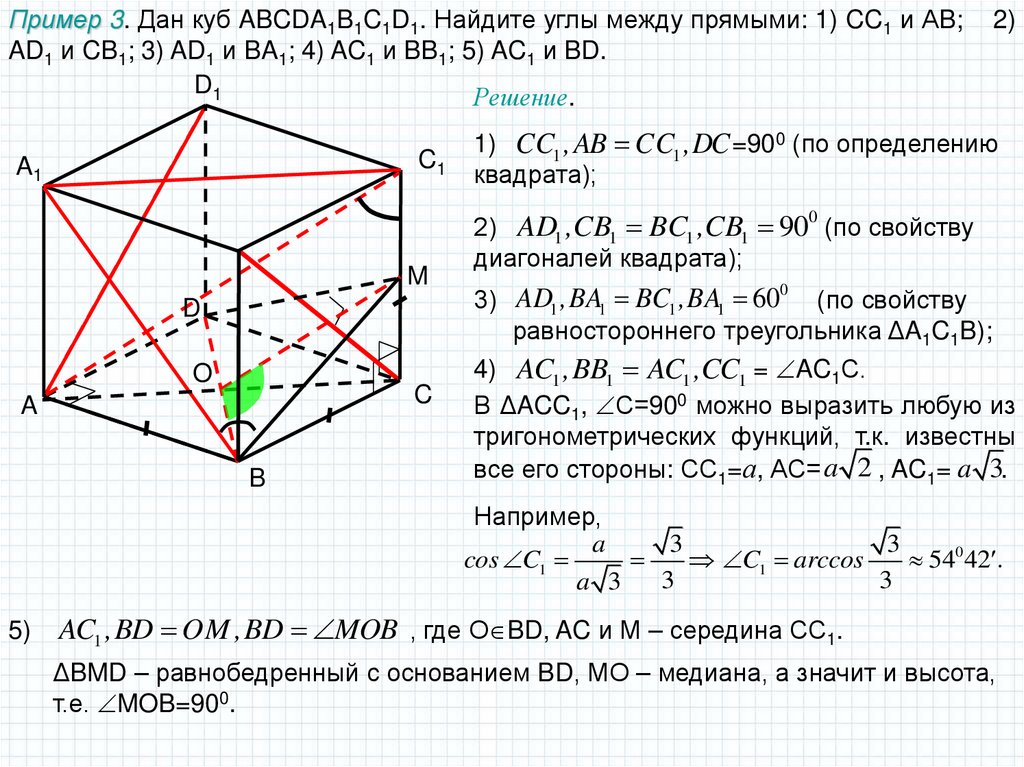
Пример 3. Дан куб ABCDA1B1C1D1. Найдите углы между прямыми: 1) CC1 и АB;
AD1 и CB1; 3) AD1 и BA1; 4) AC1 и BB1; 5) AC1 и BD.
D1
Решение.
C1
A1
2)
1) CC1 , AB CC1 ,DC =900 (по определению
квадрата);
2) AD1 ,CB1 BC1 ,CB1 90 (по свойству
диагоналей квадрата);
0
M
D
O
C
A
B
0
3) AD1 ,BA1 BC1 ,BA1 60 (по свойству
равностороннего треугольника ΔA1C1B);
4) AC1 ,BB1 AC1 ,CC1 = AC1С.
В ΔACC1, С=900 можно выразить любую из
тригонометрических функций, т.к. известны
все его стороны: СС1=а, АС= a 2 , AC1= a 3.
Например,
a
3
3
cos C1
C1 arccos
540 42
3
3
a 3
5)
AC1 ,BD OM ,BD MOB , где О BD, AC и М – середина СС1.
ΔBMD – равнобедренный с основанием BD, МО – медиана, а значит и высота,
т.е. MOB=900.

7.

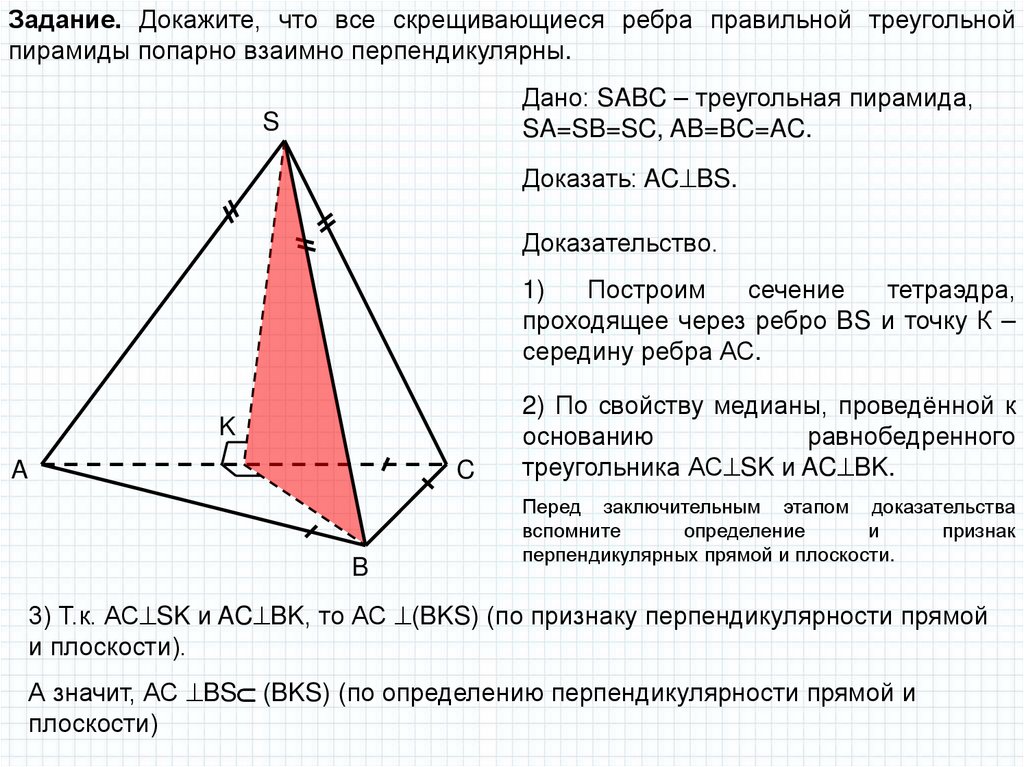
Задание. Докажите, что все скрещивающиеся ребра правильной треугольной
пирамиды попарно взаимно перпендикулярны.
Дано: SABC – треугольная пирамида,
SA=SB=SC, AB=BC=AC.
S
Доказать: AC BS.
Доказательство.
1)
Построим
сечение
тетраэдра,
проходящее через ребро BS и точку К –
середину ребра АС.
K
A
C
B
2) По свойству медианы, проведённой к
основанию
равнобедренного
треугольника АС SK и AC BK.
Перед заключительным этапом доказательства
вспомните
определение
и
признак
перпендикулярных прямой и плоскости.
3) Т.к. АС SK и AC BK, то АС (BKS) (по признаку перпендикулярности прямой
и плоскости).
А значит, АС BS (BKS) (по определению перпендикулярности прямой и
плоскости)

8.

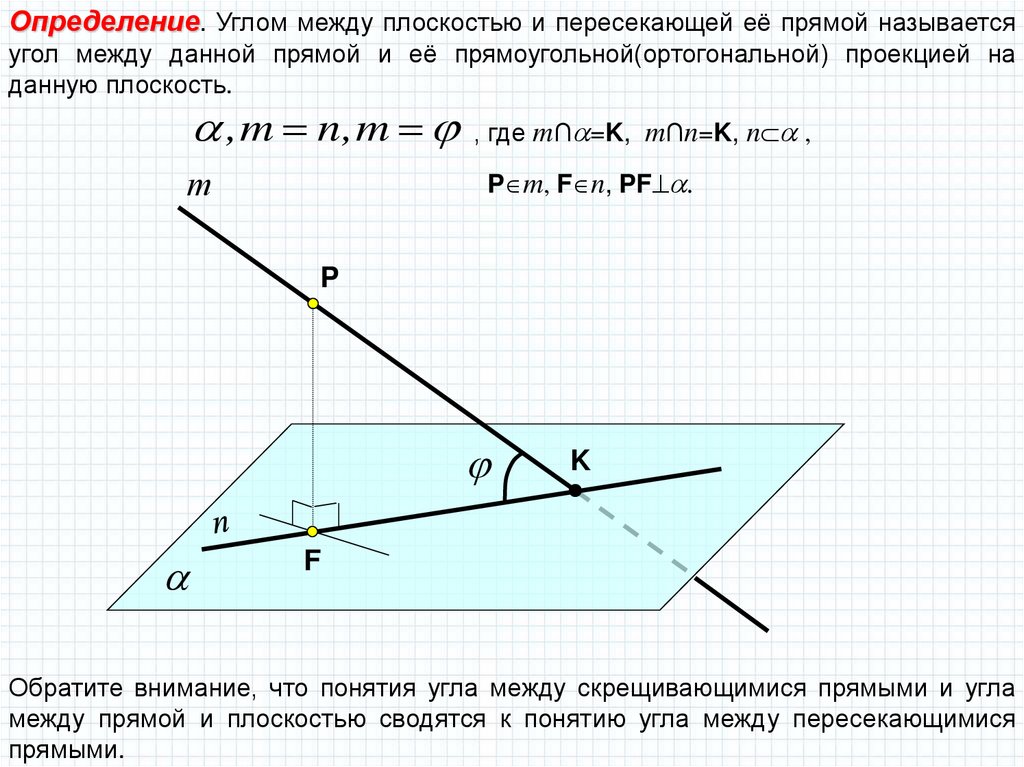
Определение. Углом между плоскостью и пересекающей её прямой называется
угол между данной прямой и её прямоугольной(ортогональной) проекцией на
данную плоскость.
,m n,m , где m∩ =K, m∩n=K, n ,
P m, F n, PF .
т
P
K
F
Обратите внимание, что понятия угла между скрещивающимися прямыми и угла
между прямой и плоскостью сводятся к понятию угла между пересекающимися
прямыми.

9.

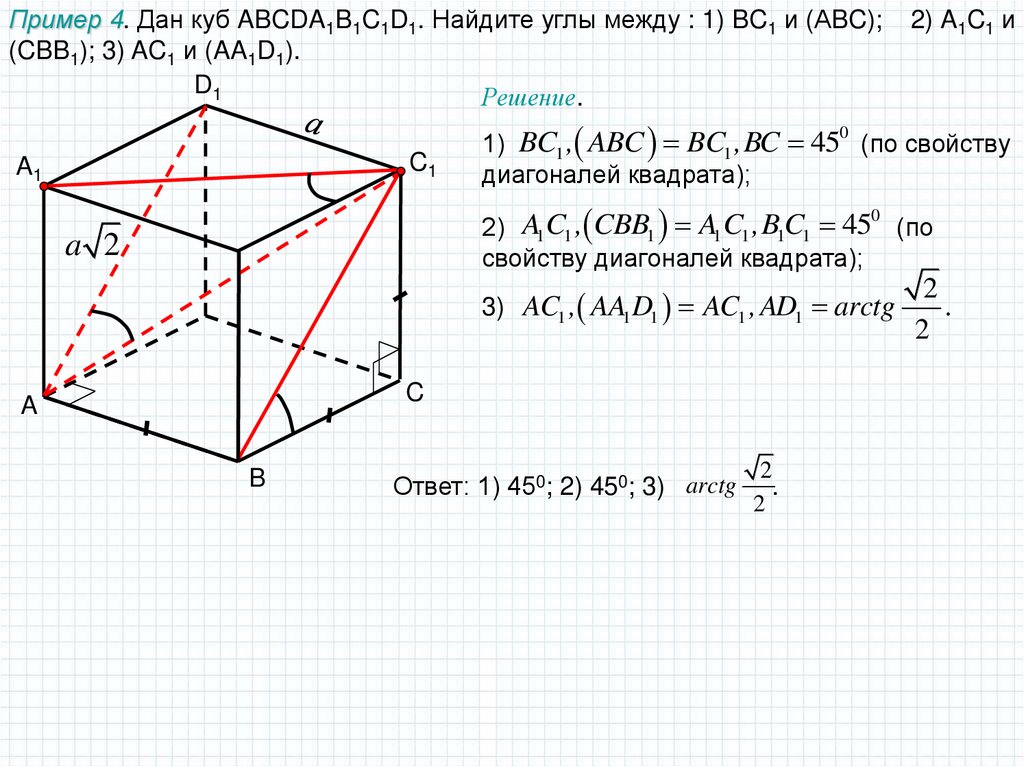
Пример 4. Дан куб ABCDA1B1C1D1. Найдите углы между : 1) BC1 и (АBC);
(CBB1); 3) AC1 и (AA1D1).
D1
Решение.
2) A1C1 и
1) BC1 , ABC BC1 ,BC 45 (по свойству
диагоналей квадрата);
0
C1
A1
2) A1 C1 , CBB1 A1 C1 ,B1C1 45 (по
свойству диагоналей квадрата);
0
a 2
3) AC1 , AA1 D1 AC1 , AD1 arctg
C
A
B
Ответ: 1) 450; 2) 450; 3) arctg
2
.
2
2
.
2