Предмет начертательной геометрии составляют теоретические основы визуализации информации о геометрических объектах

1.

Предмет начертательной геометрии составляют теоретические
основы визуализации информации о геометрических объектах,
отношения между ними и их графическое отображения на
плоскости
Изображение
объекта,
которое
позволяет
взаимосвязь элементов объекта, называют полным.
определять
Изображения, по которым можно определить размеры объекта,
называется метрически определенными
Правила построения изображений основаны на методе проекций.

2.

В курсе начертательной геометрии изучаются:
Методы отображения пространственных объектов на
плоскости;
Способы графического и аналитического решения различных
геометрических задач;
Приемы увеличения наглядности и визуальной достоверности
изображений проецируемого объекта;
Способы преобразования и исследования геометрических
свойств изображенного объекта;
Основы моделирования геометрических объектов ;
Приемы выполнения изображений с помощью графических
редакторов.

3.

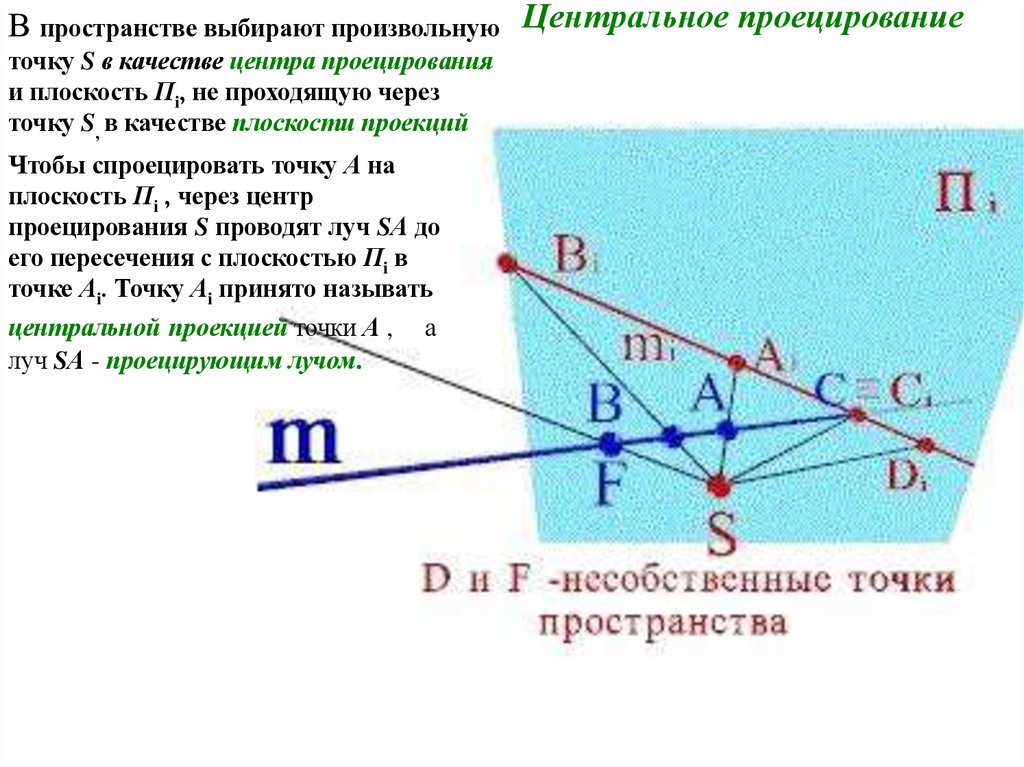
В пространстве выбирают произвольную Центральное проецирование
точку S в качестве центра проецирования
и плоскость Пi, не проходящую через
точку S, в качестве плоскости проекций
Чтобы спроецировать точку А на
плоскость Пi , через центр
проецирования S проводят луч SА до
его пересечения с плоскостью Пi в
точке Аi. Точку Аi принято называть
центральной проекцией точки А ,
луч SА - проецирующим лучом.
а

4.

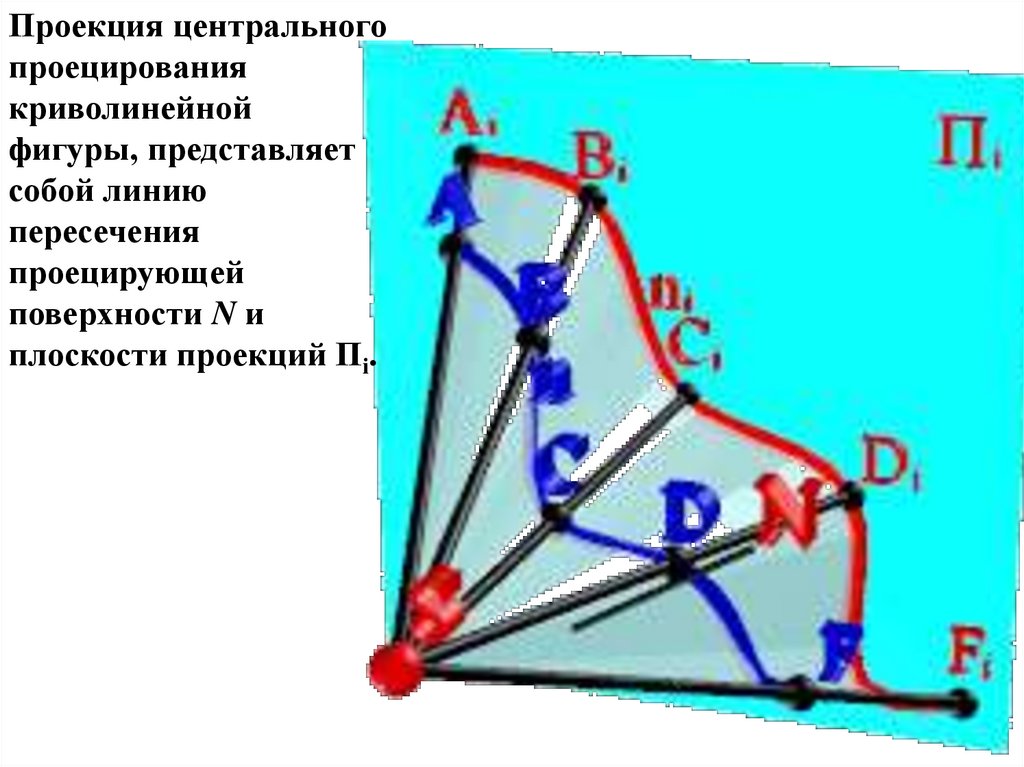
Проекция центрального
проецирования
криволинейной
фигуры, представляет
собой линию
пересечения
проецирующей
поверхности N и
плоскости проекций Пi.

5.

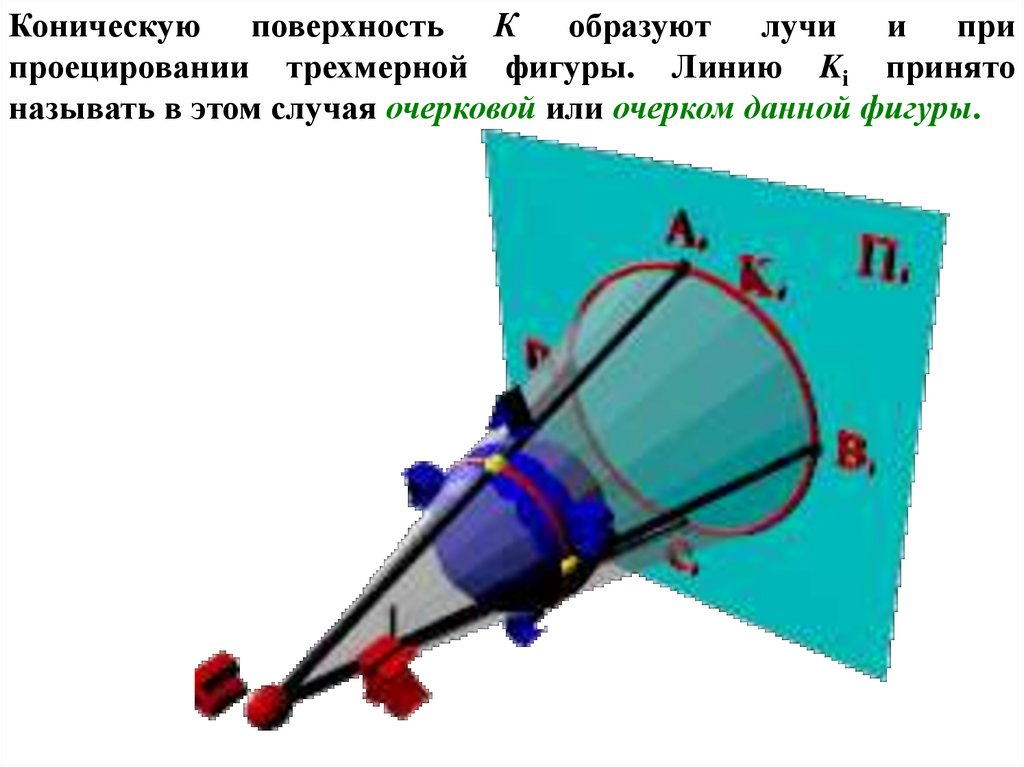
Коническую поверхность К образуют лучи и при
проецировании трехмерной фигуры. Линию Ki принято
называть в этом случая очерковой или очерком данной фигуры.

6.

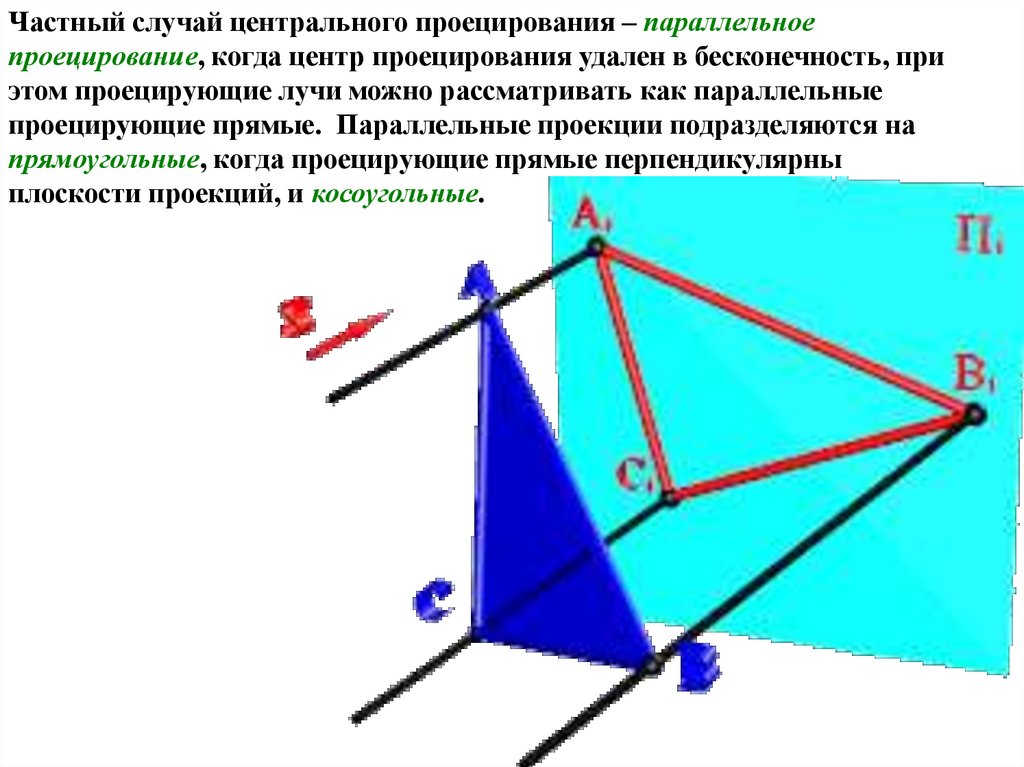
Частный случай центрального проецирования – параллельное
проецирование, когда центр проецирования удален в бесконечность, при
этом проецирующие лучи можно рассматривать как параллельные
проецирующие прямые. Параллельные проекции подразделяются на
прямоугольные, когда проецирующие прямые перпендикулярны
плоскости проекций, и косоугольные.

7.

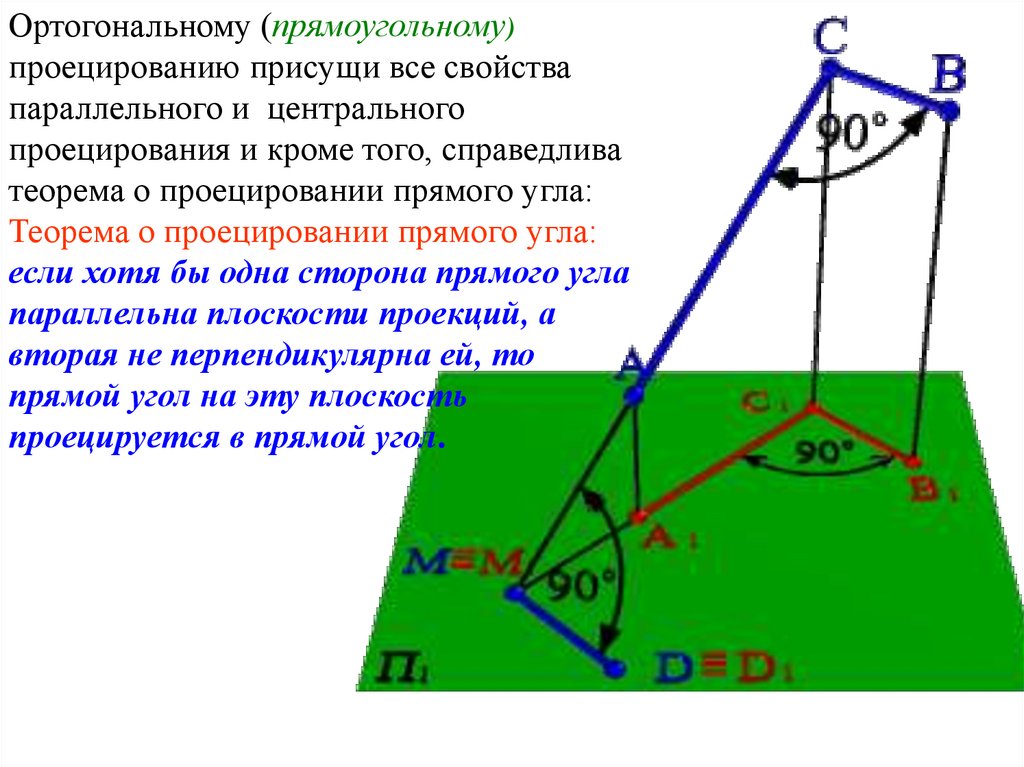
Ортогональному (прямоугольному)
проецированию присущи все свойства
параллельного и центрального
проецирования и кроме того, справедлива
теорема о проецировании прямого угла:
Теорема о проецировании прямого угла:
если хотя бы одна сторона прямого угла
параллельна плоскости проекций, а
вторая не перпендикулярна ей, то
прямой угол на эту плоскость
проецируется в прямой угол.

8.

Проекции с числовыми отметками
В проекциях с числовыми
отметками плоскость проекций Пi
называют плоскостью нулевого
уровня и обозначают П0.
Сущность метода состоит в том, что на
плоскость П0 ортогонально
проецируют точку и вместе с
проекцией точки задают ее расстояние
до плоскости П0. Это расстояние
называют числовой отметкой точки и
задают обычно в метрах.

9.

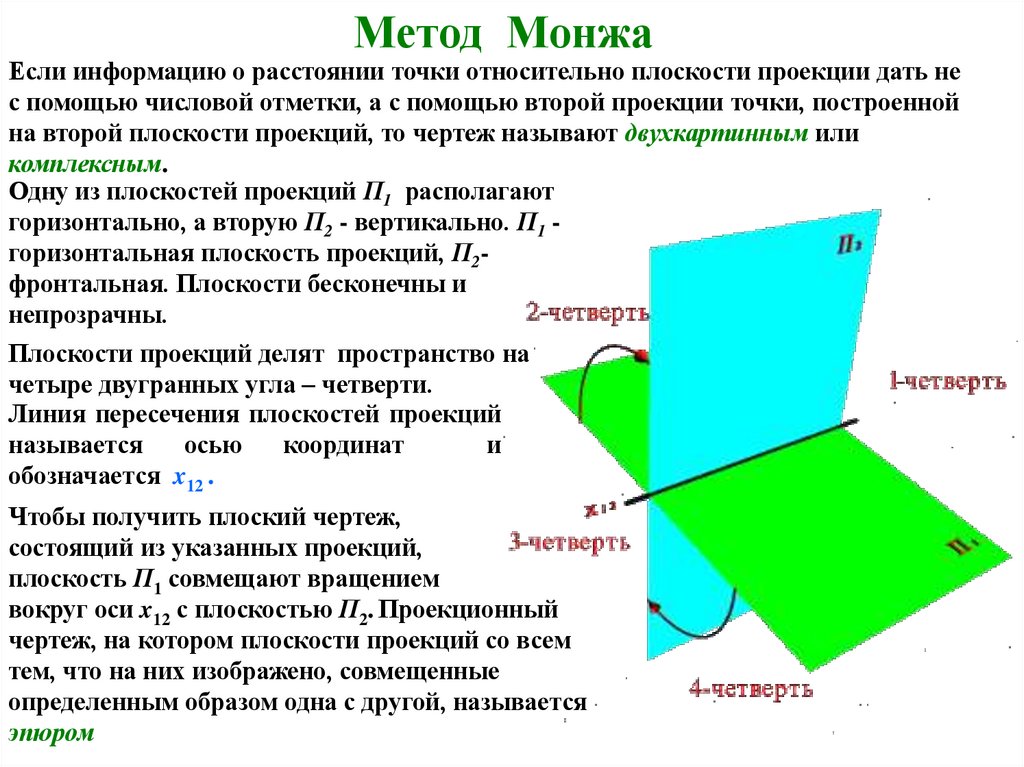
Метод Монжа
Если информацию о расстоянии точки относительно плоскости проекции дать не
с помощью числовой отметки, а с помощью второй проекции точки, построенной
на второй плоскости проекций, то чертеж называют двухкартинным или
комплексным.
Одну из плоскостей проекций П1 располагают
горизонтально, а вторую П2 - вертикально. П1 горизонтальная плоскость проекций, П2фронтальная. Плоскости бесконечны и
непрозрачны.
Плоскости проекций делят пространство на
четыре двугранных угла – четверти.
Линия пересечения плоскостей проекций
называется
осью
координат
и
обозначается x12 .
Чтобы получить плоский чертеж,
состоящий из указанных проекций,
плоскость П1 совмещают вращением
вокруг оси x12 с плоскостью П2. Проекционный
чертеж, на котором плоскости проекций со всем
тем, что на них изображено, совмещенные
определенным образом одна с другой, называется
эпюром

10.

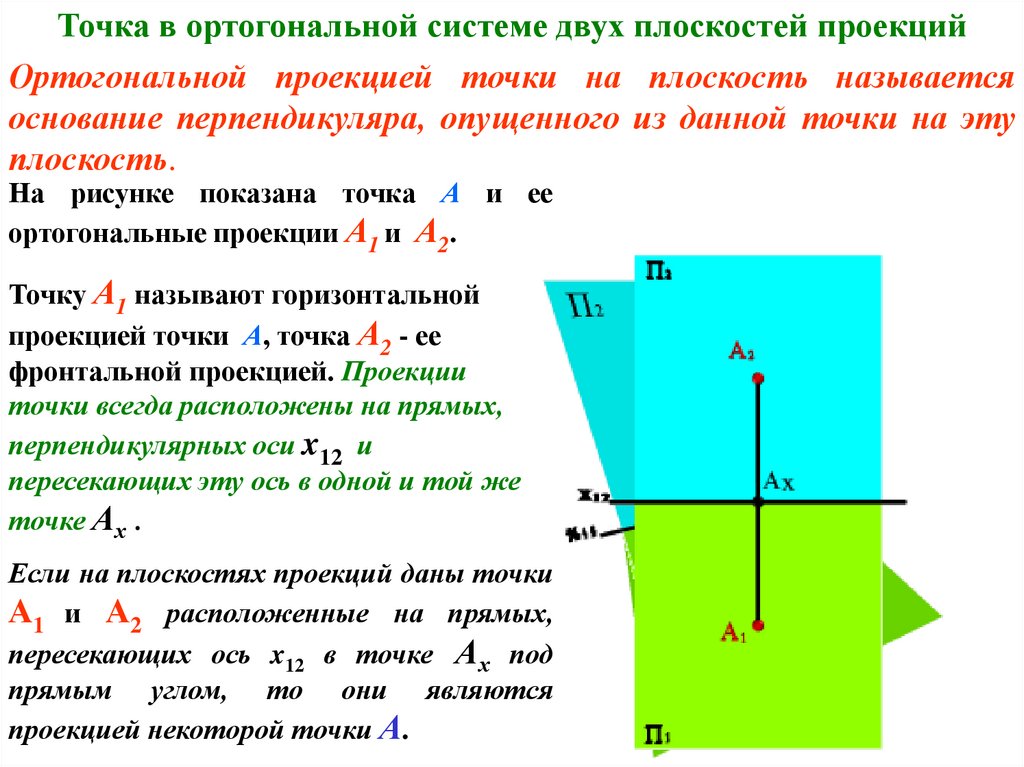
Точка в ортогональной системе двух плоскостей проекций
Ортогональной проекцией точки на плоскость называется
основание перпендикуляра, опущенного из данной точки на эту
плоскость.
На рисунке показана точка А и ее
ортогональные проекции А1 и А2.
Точку А1 называют горизонтальной
проекцией точки А, точка А2 - ее
фронтальной проекцией. Проекции
точки всегда расположены на прямых,
перпендикулярных оси x12 и
пересекающих эту ось в одной и той же
точке Ах .
Если на плоскостях проекций даны точки
А1 и А2 расположенные на прямых,
пересекающих ось x12 в точке Ах под
прямым углом, то они являются
проекцией некоторой точки А.

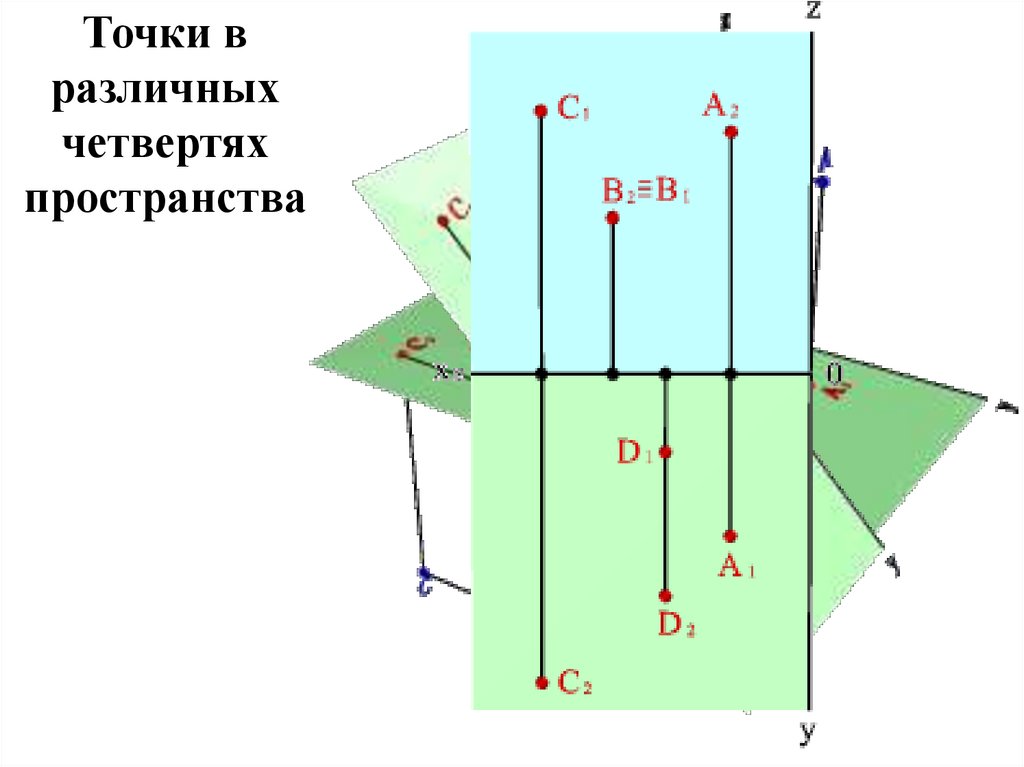
11.

Точки в
различных
четвертях
пространства

12.

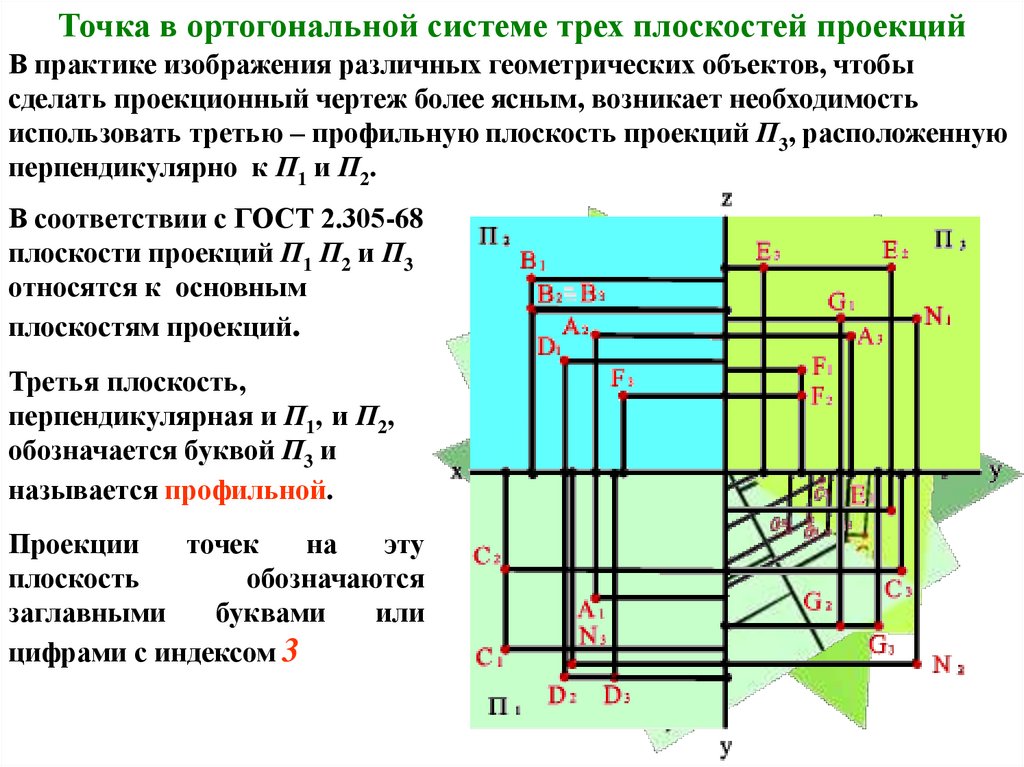
Точка в ортогональной системе трех плоскостей проекций
В практике изображения различных геометрических объектов, чтобы
сделать проекционный чертеж более ясным, возникает необходимость
использовать третью – профильную плоскость проекций П3, расположенную
перпендикулярно к П1 и П2.
В соответствии с ГОСТ 2.305-68
плоскости проекций П1 П2 и П3
относятся к основным
плоскостям проекций.
Третья плоскость,
перпендикулярная и П1, и П2,
обозначается буквой П3 и
называется профильной.
Проекции
точек
на
эту
плоскость
обозначаются
заглавными
буквами
или
цифрами с индексом 3

13.

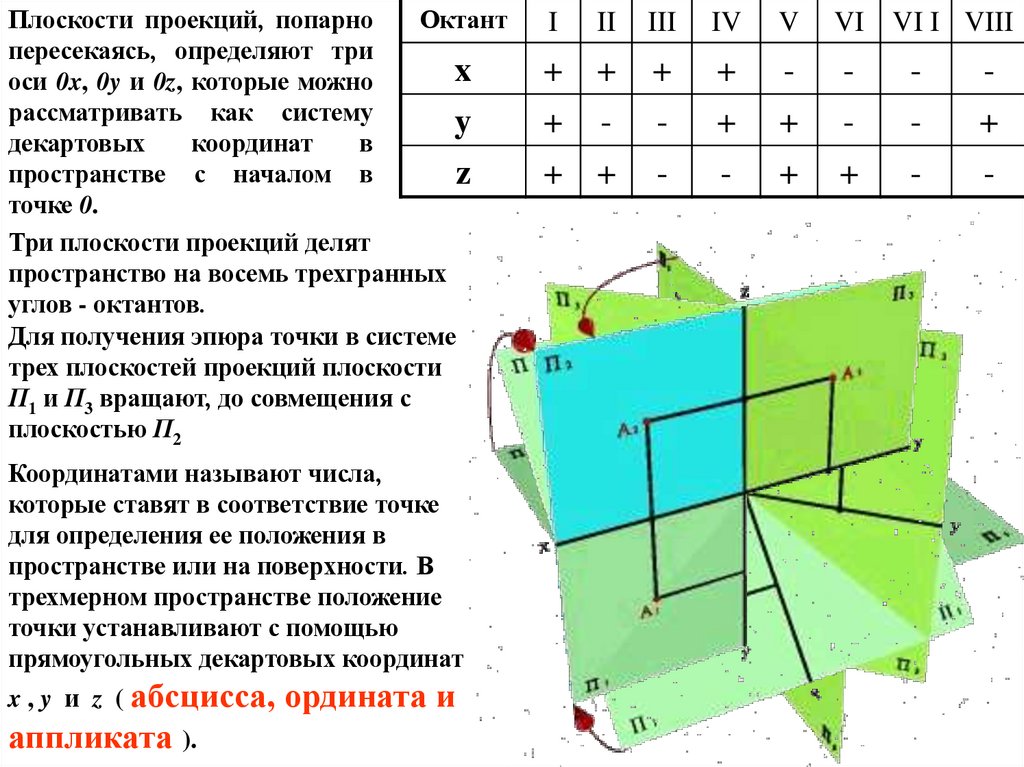
Плоскости проекций, попарно
Октант
пересекаясь, определяют три
x
оси 0x, 0y и 0z, которые можно
рассматривать как систему
y
декартовых
координат
в
пространстве с началом в
z
точке 0.
Три плоскости проекций делят
пространство на восемь трехгранных
углов - октантов.
Для получения эпюра точки в системе
трех плоскостей проекций плоскости
П1 и П3 вращают, до совмещения с
плоскостью П2
Координатами называют числа,
которые ставят в соответствие точке
для определения ее положения в
пространстве или на поверхности. В
трехмерном пространстве положение
точки устанавливают с помощью
прямоугольных декартовых координат
x , y и z ( абсцисса, ордината и
аппликата ).
I
II
III
IV
V
VI VI I VIII
+ +
+
+
-
-
-
-
+
-
-
+
+
-
-
+
+ +
-
-
+
+
-
-

14.

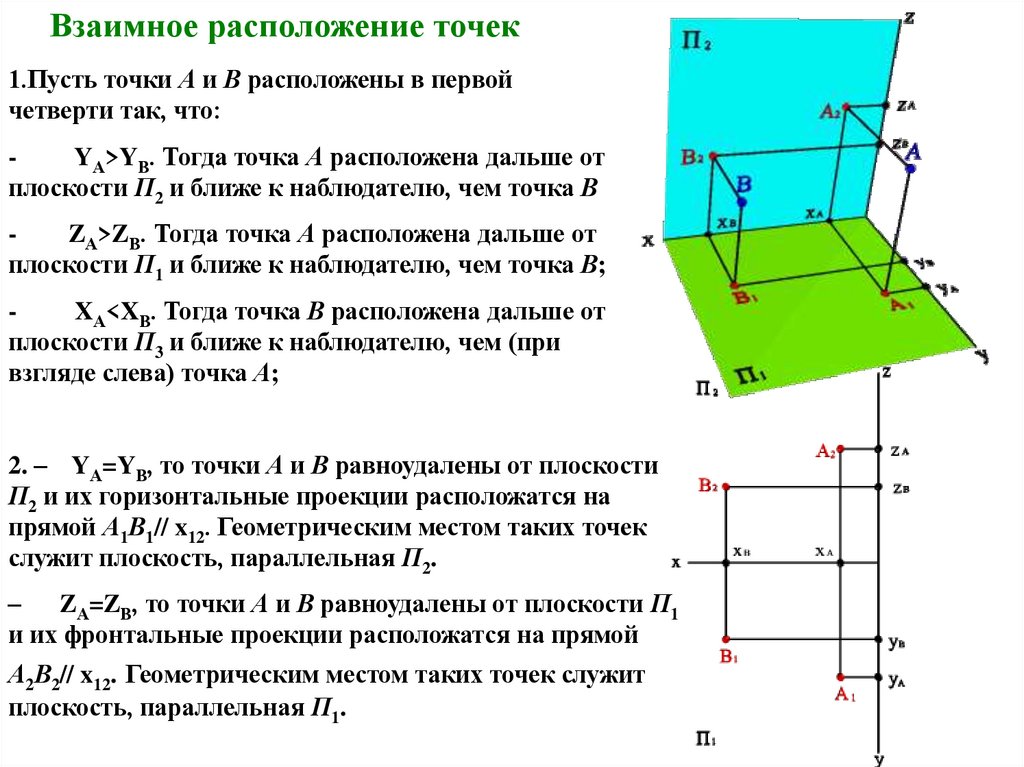
Взаимное расположение точек
1.Пусть точки А и В расположены в первой
четверти так, что:
YА>YВ. Тогда точка А расположена дальше от
плоскости П2 и ближе к наблюдателю, чем точка В
ZА>ZВ. Тогда точка А расположена дальше от
плоскости П1 и ближе к наблюдателю, чем точка В;
XА<XВ. Тогда точка В расположена дальше от
плоскости П3 и ближе к наблюдателю, чем (при
взгляде слева) точка А;
2. – YА=YВ, то точки А и В равноудалены от плоскости
П2 и их горизонтальные проекции расположатся на
прямой А1В1// x12. Геометрическим местом таких точек
служит плоскость, параллельная П2.
–
ZА=ZВ, то точки А и В равноудалены от плоскости П1
и их фронтальные проекции расположатся на прямой
А2В2// x12. Геометрическим местом таких точек служит
плоскость, параллельная П1.

15.

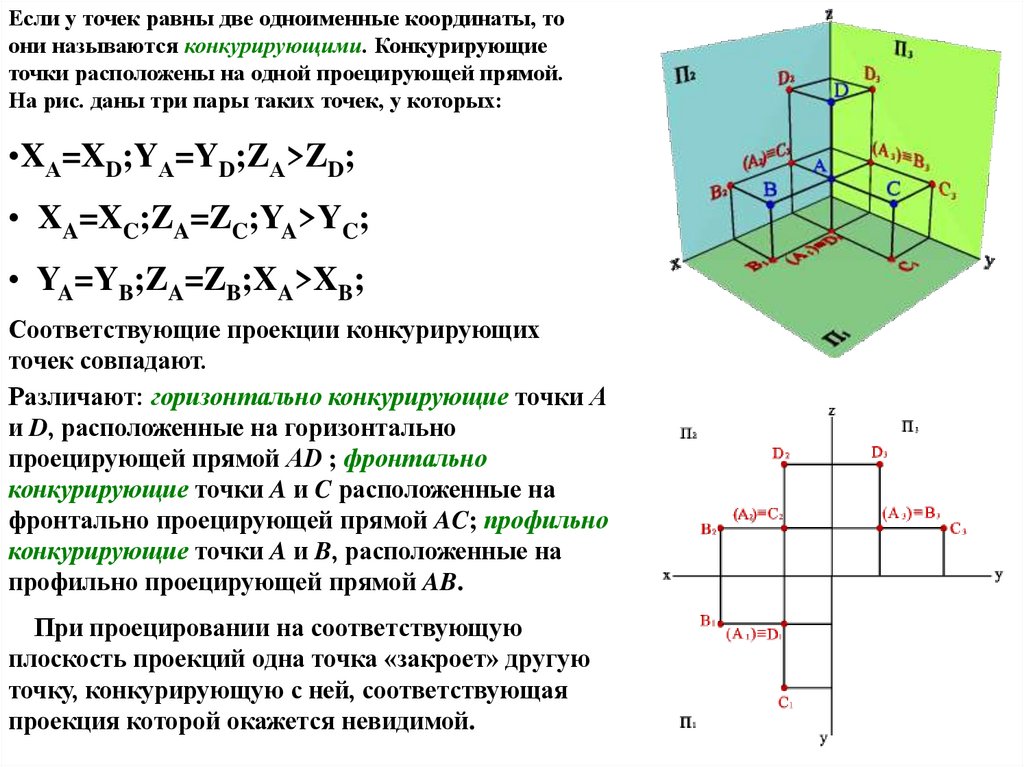
Если у точек равны две одноименные координаты, то
они называются конкурирующими. Конкурирующие
точки расположены на одной проецирующей прямой.
На рис. даны три пары таких точек, у которых:
•XА=XD;YА=YD;ZА>ZD;
• XA=XC;ZA=ZC;YA>YC;
• YA=YB;ZA=ZB;XA>XB;
Соответствующие проекции конкурирующих
точек совпадают.
Различают: горизонтально конкурирующие точки А
и D, расположенные на горизонтально
проецирующей прямой АD ; фронтально
конкурирующие точки A и C расположенные на
фронтально проецирующей прямой AC; профильно
конкурирующие точки A и B, расположенные на
профильно проецирующей прямой AB.
При проецировании на соответствующую
плоскость проекций одна точка «закроет» другую
точку, конкурирующую с ней, соответствующая
проекция которой окажется невидимой.

16.

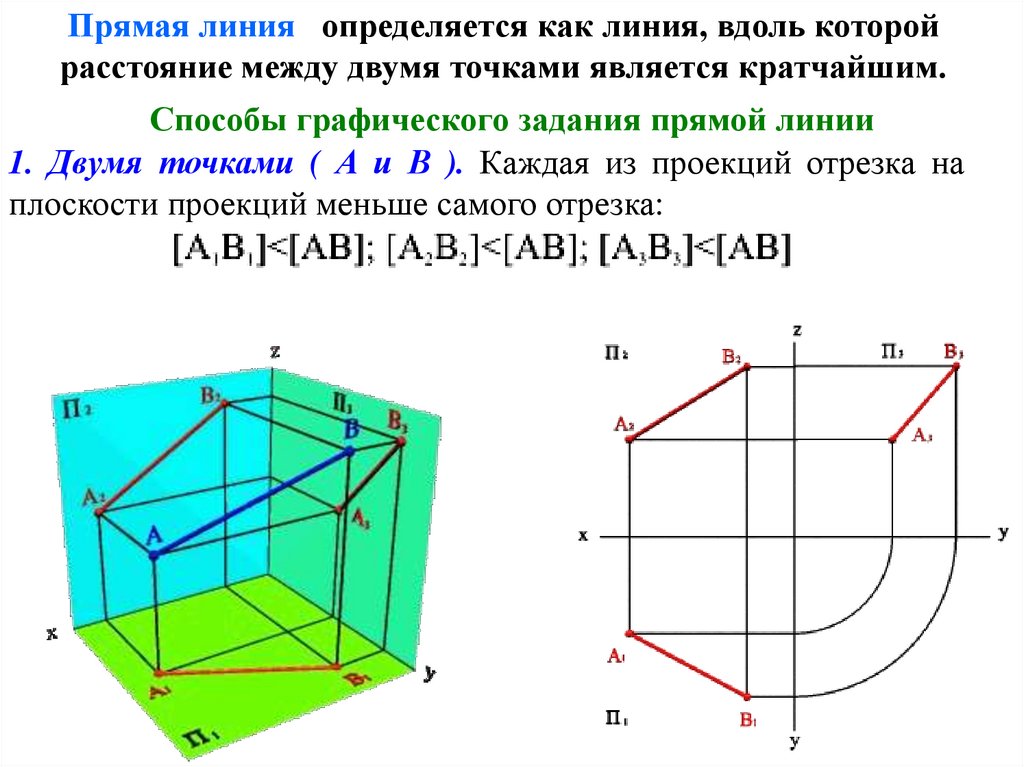
Прямая линия определяется как линия, вдоль которой
расстояние между двумя точками является кратчайшим.
Способы графического задания прямой линии
1. Двумя точками ( А и В ). Каждая из проекций отрезка на
плоскости проекций меньше самого отрезка:

17.

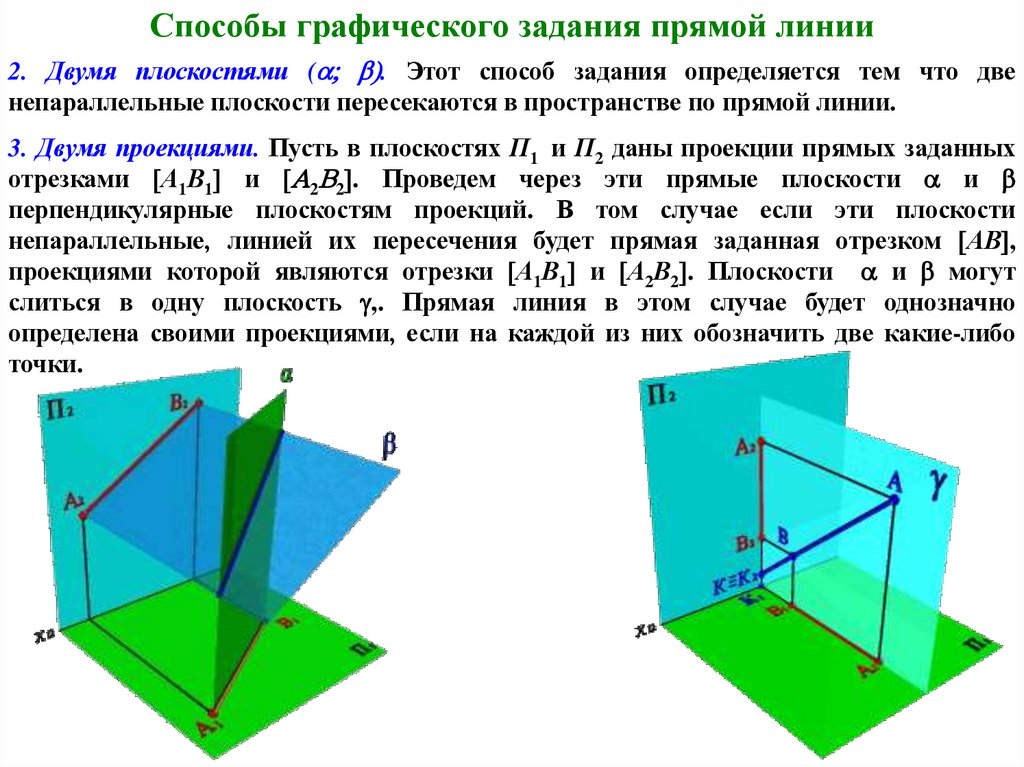
Способы графического задания прямой линии
2. Двумя плоскостями ( . Этот способ задания определяется тем что две
непараллельные плоскости пересекаются в пространстве по прямой линии.
3. Двумя проекциями. Пусть в плоскостях П1 и П2 даны проекции прямых заданных
отрезками А1В1 и 2 2 . Проведем через эти прямые плоскости и
перпендикулярные плоскостям проекций. В том случае если эти плоскости
непараллельные, линией их пересечения будет прямая заданная отрезком АВ ,
проекциями которой являются отрезки А1В1 и А2В2 . Плоскости и могут
слиться в одну плоскость ,. Прямая линия в этом случае будет однозначно
определена своими проекциями, если на каждой из них обозначить две какие-либо
точки.

18.

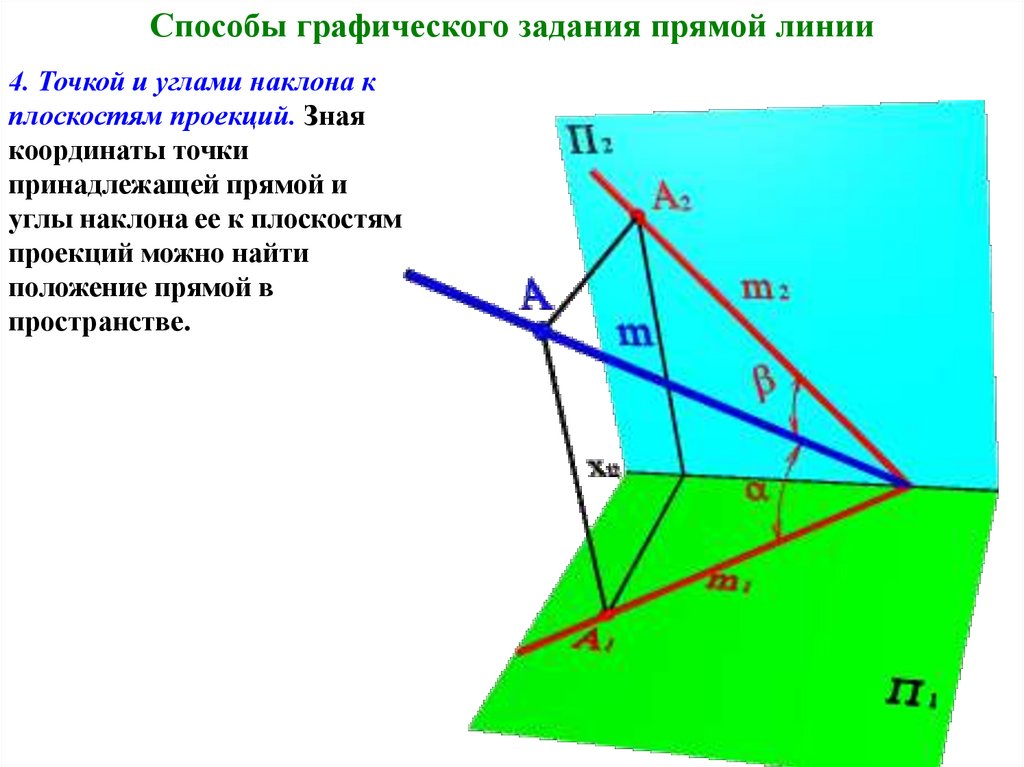
Способы графического задания прямой линии
4. Точкой и углами наклона к
плоскостям проекций. Зная
координаты точки
принадлежащей прямой и
углы наклона ее к плоскостям
проекций можно найти
положение прямой в
пространстве.

19.

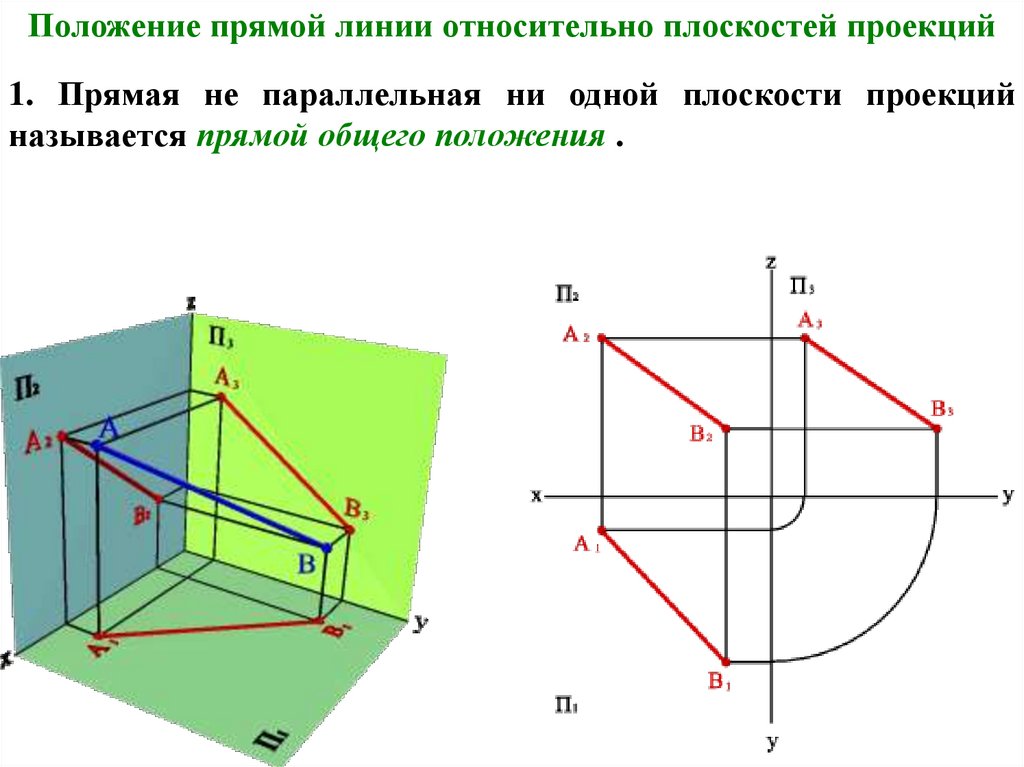
Положение прямой линии относительно плоскостей проекций
1. Прямая не параллельная ни одной плоскости проекций
называется прямой общего положения .

20.

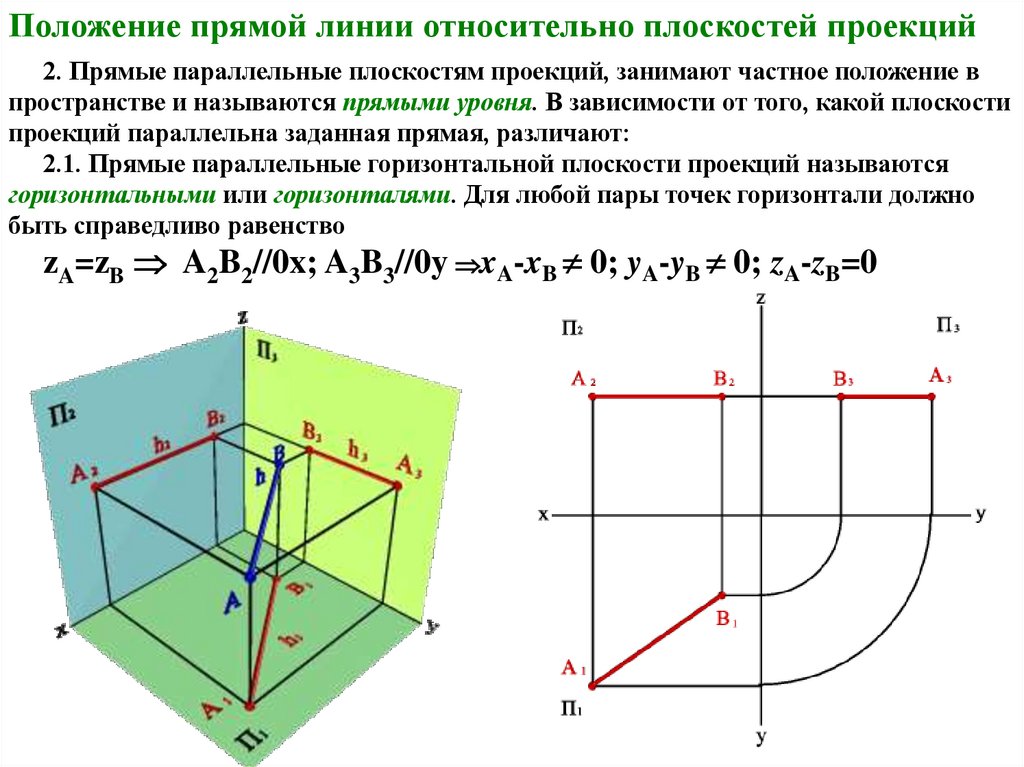
Положение прямой линии относительно плоскостей проекций
2. Прямые параллельные плоскостям проекций, занимают частное положение в
пространстве и называются прямыми уровня. В зависимости от того, какой плоскости
проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются
горизонтальными или горизонталями. Для любой пары точек горизонтали должно
быть справедливо равенство
zA=zB A2B2//0x; A3B3//0y xA-xB 0; yA-yB 0; zA-zB=0

21.

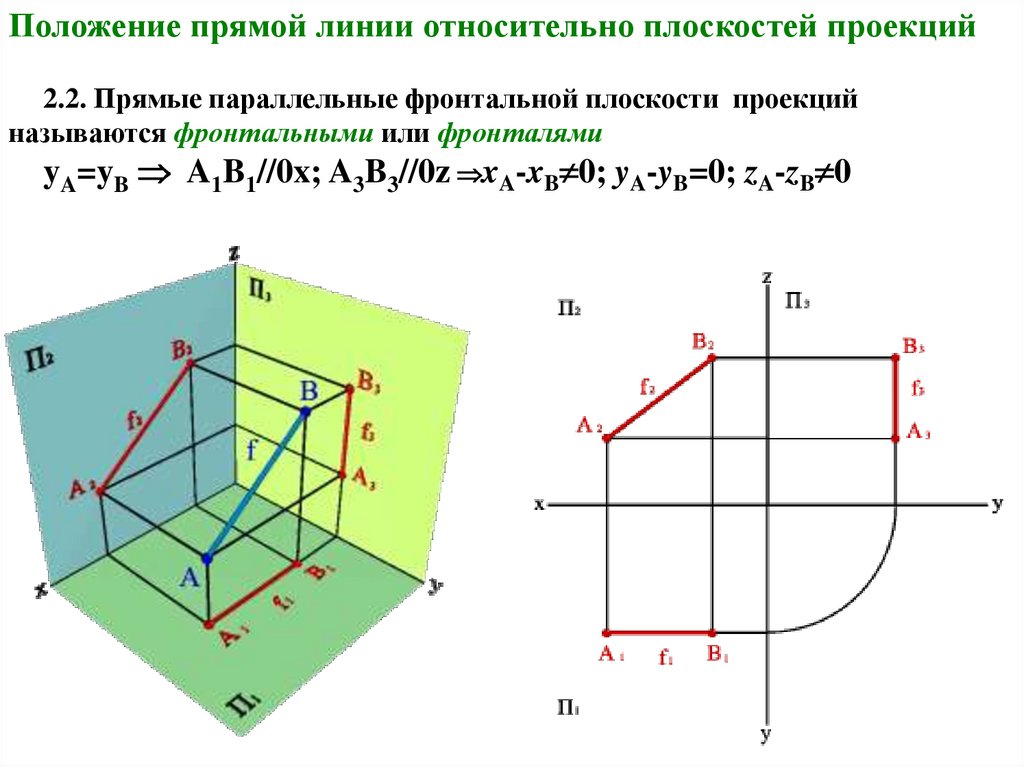
Положение прямой линии относительно плоскостей проекций
2.2. Прямые параллельные фронтальной плоскости проекций
называются фронтальными или фронталями
yA=yB A1B1//0x; A3B3//0z xA-xB 0; yA-yB=0; zA-zB 0

22. Положение прямой линии относительно плоскостей проекций

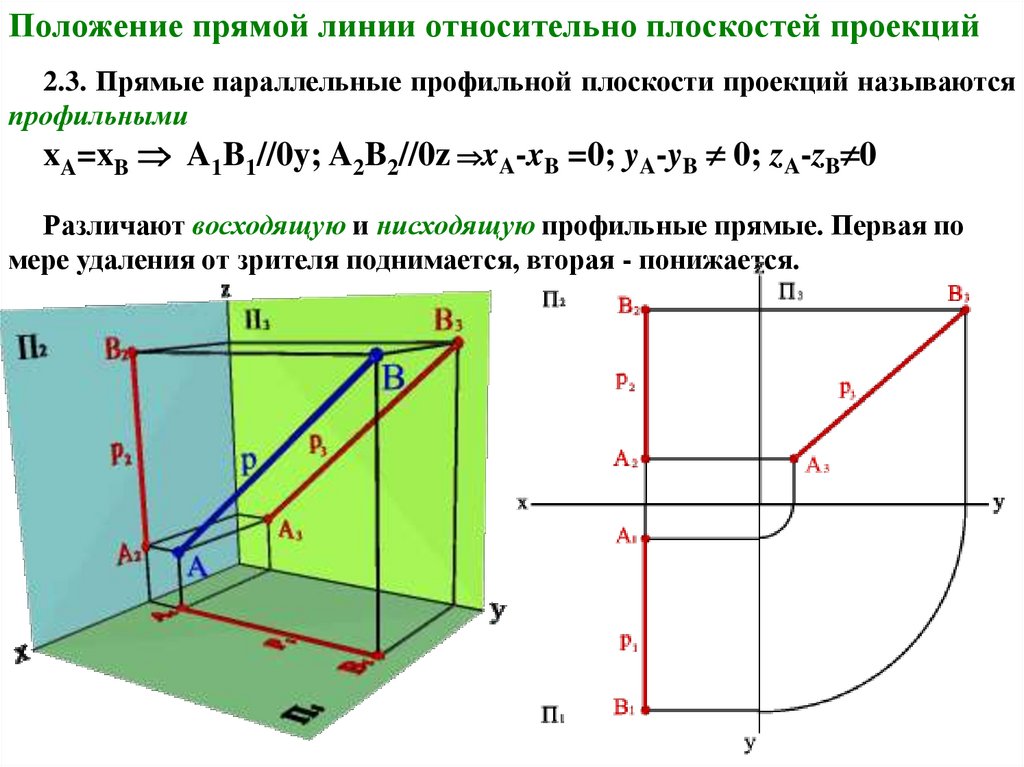
2.3. Прямые параллельные профильной плоскости проекций называются
профильными
xA=xB A1B1//0y; A2B2//0z xA-xB =0; yA-yB 0; zA-zB 0
Различают восходящую и нисходящую профильные прямые. Первая по
мере удаления от зрителя поднимается, вторая - понижается.

23.

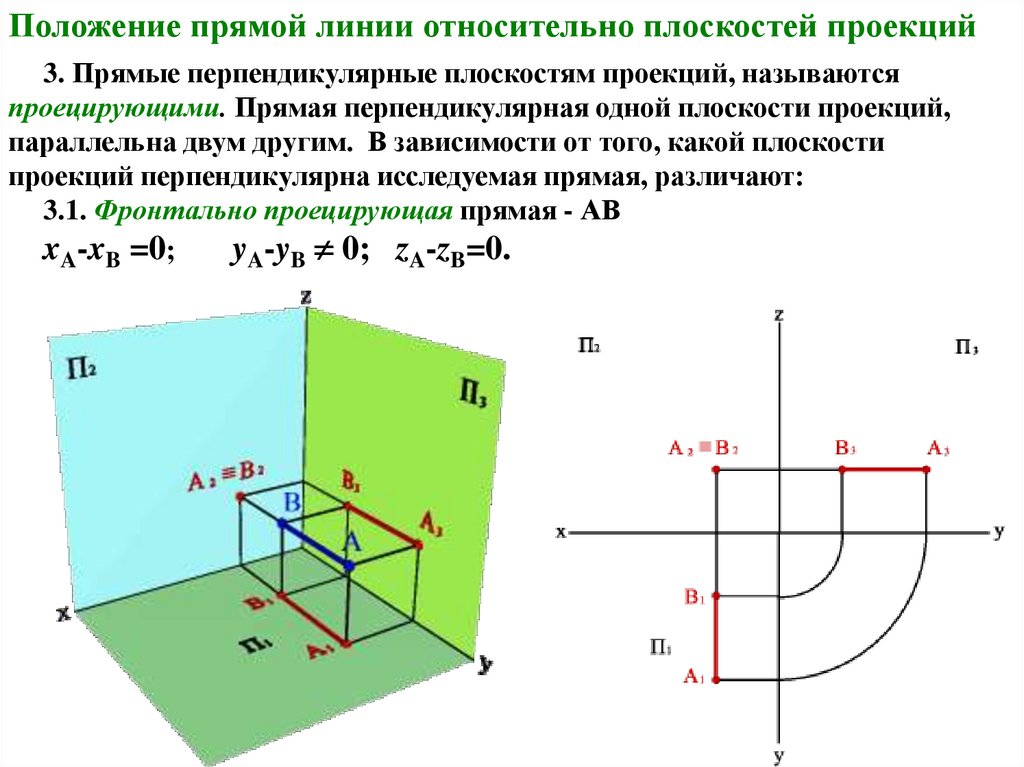
Положение прямой линии относительно плоскостей проекций
3. Прямые перпендикулярные плоскостям проекций, называются
проецирующими. Прямая перпендикулярная одной плоскости проекций,
параллельна двум другим. В зависимости от того, какой плоскости
проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально проецирующая прямая - АВ
xA-xB =0;
yA-yB 0; zA-zB=0.

24.

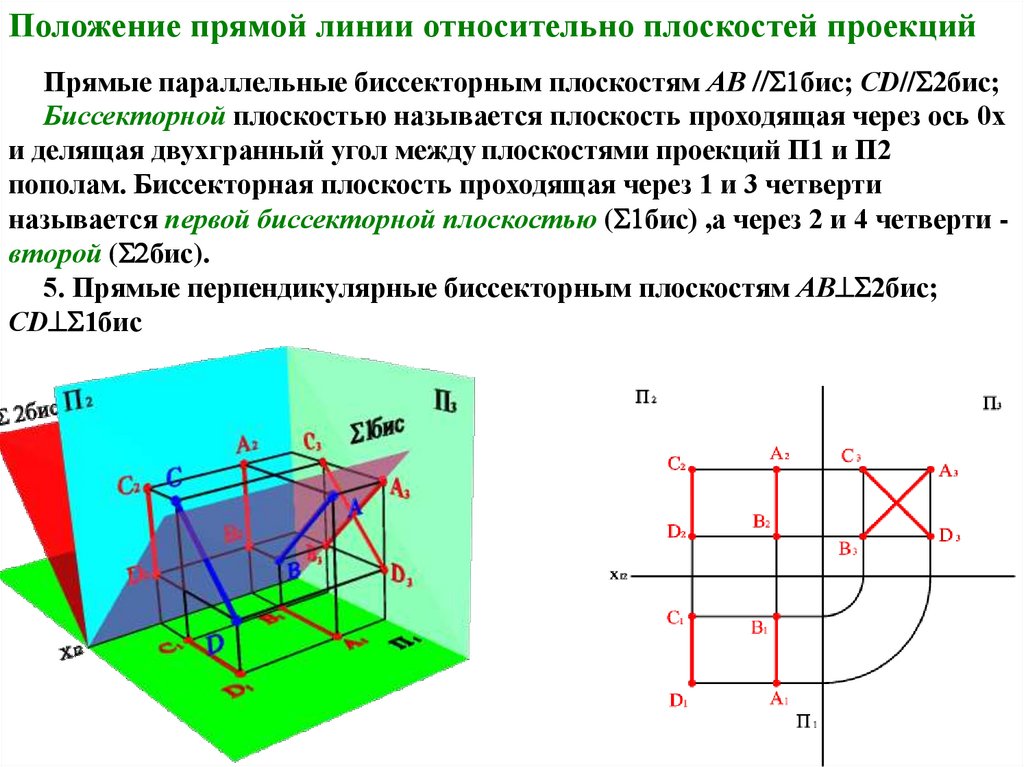
Положение прямой линии относительно плоскостей проекций
Прямые параллельные биссекторным плоскостям АВ бис; СD// 2бис;
Биссекторной плоскостью называется плоскость проходящая через ось 0х
и делящая двухгранный угол между плоскостями проекций П1 и П2
пополам. Биссекторная плоскость проходящая через 1 и 3 четверти
называется первой биссекторной плоскостью ( бис) ,а через 2 и 4 четверти второй ( бис).
5. Прямые перпендикулярные биссекторным плоскостям АВ 2бис;
СD 1бис