Similar presentations:
Системы счисления
1.
Тема 1.Системы счисления
Лабораторные занятия
© 2016, Конах В.В.
1
2.
Системы счисления• Системой счисления называется совокупность правил
записи чисел.
• Системы счисления подразделяются на позиционные и
непозиционные.
• Наиболее совершенными являются позиционные
системы счисления, т.е. системы записи чисел, в которых
значение цифры в числе зависит от ее положения
(позиции).
• Системы счисления, в которых каждой цифре
соответствует величина, не зависящая от ее места в
записи числа, называются непозиционными.
• Позиционные системы счисления – результат
исторического развития непозиционных систем
счисления.
© 2016, Конах В.В.
2
3.
Единичная система• В древние времена, когда люди начали
считать, появилась потребность в записи
чисел. Количество предметов
обозначалось черточкой или зарубкой на
твердой поверхности (камне, глине,
дереве). Ученые назвали эту систему
записи чисел единичной (палочной).
© 2016, Конах В.В.
3
4.
Древнеегипетская десятичнаянепозиционная система
• Во второй половине третьего тысячелетия до н.э.
для обозначения чисел 1, 10, 102, 103
использовались специальные знаки (цифры):
• Так число 245 древние египтяне записывали так:
• В основе как палочной, так и древнеегипетской
систем лежал простой принцип сложения, согласно
которому значение числа равно сумме значений
цифр, участвующих в его записи.
© 2016, Конах В.В.
4
5.
Вавилонская шестидесятеричнаясистема
• Две тысячи лет до н.э. числа в этой системе
состояли из знаков двух видов:
–прямой клин для обозначения
единиц и
–лежачий клин для обозначения
десятков.
• Число 32 записывалось так:
© 2016, Конах В.В.
5
6.
• Число 60 снова обозначалось тем жезнаком
что и 1. Этим же знаком
обозначались числа 3600=602, 216000=603
и все другие степени 60.
• Для определения значения числа надо
было изображение разбить на разряды
справа налево. Чередование групп
одинаковых знаков (цифр)
соответствовало чередованию разрядов:
© 2016, Конах В.В.
6
7.
Здесь записано число 132=2*60+10+2*1. Значениечисла определяется
по значениям составляющих
.
его цифр, но с учетом того, что цифры в каждом
последующем разряде значат в 60 раз больше тех
же цифр в предыдущем разряде, в итоге
получается, что все цифры от 1 до 59
записываются в десятичной непозиционной
системе, а все число – в позиционной системе с
основанием 60.
© 2016, Конах В.В.
7
8.
Число 92=60+32:444=7*60+24:
Запись числа была неоднозначной, так как не
существовало цифры “нуль”. Так запись числа 92
могла соответствовать и числу 3632=3600+32 и т.д.
Поэтому в последствии появился специальный
символ для обозначения пропущенного разряда: .
© 2016, Конах В.В.
8
9.
• Число 3632=3600+32 стало записыватьсятак:
• Но в конце числа этот знак не ставился, т.е.
это не был “нуль” в нынешнем понимании.
• Эта система сыграла большую роль в
развитии математики и астрономии. До сих
пор час делится на 60 минут, минута на 60
секунд, а окружность на 360 градусов.
© 2016, Конах В.В.
9
10.
Римская система• Она принципиально не намного
отличается от египетской. В ней для
обозначения чисел используются
заглавные латинские буквы:
• I – 1;
C – 100;
• V – 5;
D – 500;
• X – 10;
M – 1000.
• L – 50;
© 2016, Конах В.В.
10
11.
Римская система• Она принципиально не намного
отличается от египетской. В ней для
обозначения чисел используются
заглавные латинские буквы:
• I – 1;
C – 100;
• V – 5;
D – 500;
• X – 10;
M – 1000.
• L – 50;
© 2016, Конах В.В.
11
12.
В этой системе:32=XXXII=(X+X+X)+(I+I)=30+2
444=CDXLIV=(D–C)+(L–X)+(V–I)=400+40+4
1976=MCMLXXVI=
= M+(M–C)+(L+X+X)+(V+I)=100+900+70+6
DLXXVII=500+50+10+10+5+1+1=577
CDXXIX=500–100+10+10+10–1=429
© 2016, Конах В.В.
12
13.
Алфавитные системыБолее совершенные непозиционные
были алфавитные системы: славянская,
ионийская (греческая), финикийская и
др. В них числа от 1 до 9 обозначали
буквами алфавита. Алфавитная система
была и в древней Руси. Числа
записывали буквами и над ними ставили
специальный знак “титло”.
© 2016, Конах В.В.
13
14.
Позиционные системы счисления• Алфавит – совокупность различных цифр,
используемых для записи чисел.
• Базис – последовательность чисел, каждое из
которых задает значение цифры “по месту”
или “вес” каждого разряда.
Базисы для 10с/с: 1, 10, 102, 103,104, … , 10n, …
2 c/c: 1, 2, 22, 23, 24, …, 2n, …
© 2016, Конах В.В.
14
15.
В общем виде для p-ичной c/с базисимеет вид:
…, p-2, p-1, 1, p, p2, p3, …, pn, …
Знаменатель p называется основанием
системы.
(Дайте другие определения основания
системы счисления.)
© 2016, Конах В.В.
15
16.
Основание позиционной системы счисления— количество различных цифр,
используемых для изображения чисел в
данной системе счисления.
© 2016, Конах В.В.
16
17.
За основание системыможно принять любое
натуральное число — два,
три, четыре и т.д.
Следовательно, возможно
бесчисленное множество
позиционных систем:
двоичная, троичная,
четверичная и т.д. Запись
чисел в каждой из систем
счисления с
основанием q означает
сокращенную запись
выражения
an-1 qn-1 + an-2 qn-2 + ... + a1 q1 + a0 q0 + a-1 q-1 +
... + a-m q-m,
© 2016,
где ai — цифры системы счисления;
n и Конах
m — В.В.
17
18.
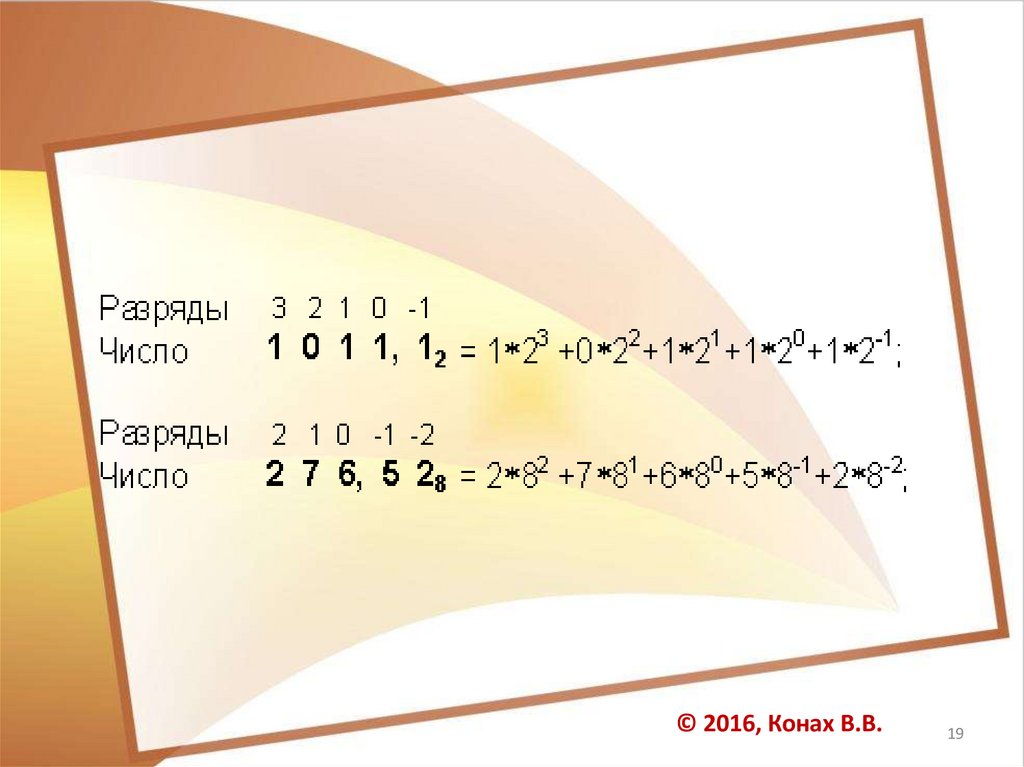
Таким образом,an-1 qn-1 + an-2 qn-2 + ... + a1 q1 + a0 q0 + a-1 q-1 + ...
+ a-m q-m — развернутая запись
числа в позиционной системе,
а
an-1 an-2 ... a1a0 a-1 ... a-m — сокращенная запись,
привычная нам.
ai — цифры системы счисления; n и m — число целых и
дробных разрядов, соответственно.
© 2016, Конах В.В.
18
19.
© 2016, Конах В.В.19
20.
• Такие системы - традиционныепозиционные системы, базис которых
образуют члены геометрической
прогрессии.
• Существуют и нетрадиционные
позиционные системы, например:
• Факториальная система с базисом:
1!, 2!, 3!, 4!, …, (n-1)!, n!, …
• Фибоначчиева система с базисом:
1, 2, 3, 5, 8, 13, 21, …
© 2016, Конах В.В.
20
21.
Какие системы счисления используютсядля общения с компьютером?
системы с основанием, являющимся целой
степенью числа 2, а именно:
двоичная (используются цифры 0, 1);
восьмеричная (используются цифры 0, 1, ..., 7);
шестнадцатеричная (для первых целых чисел от
нуля до девяти используются цифры 0, 1, ..., 9, а
для следующих чисел — от десяти до пятнадцати
— в качестве цифр используются символы A, B, C,
D, E, F).
© 2016, Конах В.В.
21
22.
Почему люди пользуются десятичнойсистемой, а компьютеры — двоичной?
Люди предпочитают десятичную
систему, вероятно, потому, что с
древних времен считали по пальцам, а
пальцев у людей по десять на руках и
ногах. Но не всегда и не везде люди
пользуются десятичной системой
счисления. В Китае, например, долгое
время пользовались пятеричной
системой счисления.
© 2016, Конах В.В.
22
23.
А компьютеры используют двоичную системупотому, что она имеет ряд преимуществ перед
другими системами:
• для ее реализации нужны технические
устройства с двумя устойчивыми состояниями
(есть ток — нет тока, намагничен — не
намагничен и т.п.), а не, например, с десятью, —
как в десятичной;
• представление информации посредством только
двух состояний надежно и помехоустойчиво;
• возможно применение аппарата булевой
алгебры для выполнения логических
преобразований информации;
• двоичная арифметика намного проще
десятичной.
© 2016, Конах В.В.
23
24.
Недостаток двоичной системы— быстрый рост числа разрядов,
необходимых для записи чисел.
Двоичная система, удобная для
компьютеров, для человека неудобна из-за
ее громоздкости и непривычной записи.
Поэтому для удобства используются
восьмеричная и шестнадцатеричная системы.
© 2016, Конах В.В.
24
25.
Числа в этих системах читаются почтитак же легко, как десятичные, требуют
соответственно в три (восьмеричная) и
в четыре (шестнадцатеричная) раза
меньше разрядов, чем в двоичной
системе (ведь числа 8 и 16 —
соответственно, третья и четвертая
степени числа 2).
© 2016, Конах В.В.
25
26.
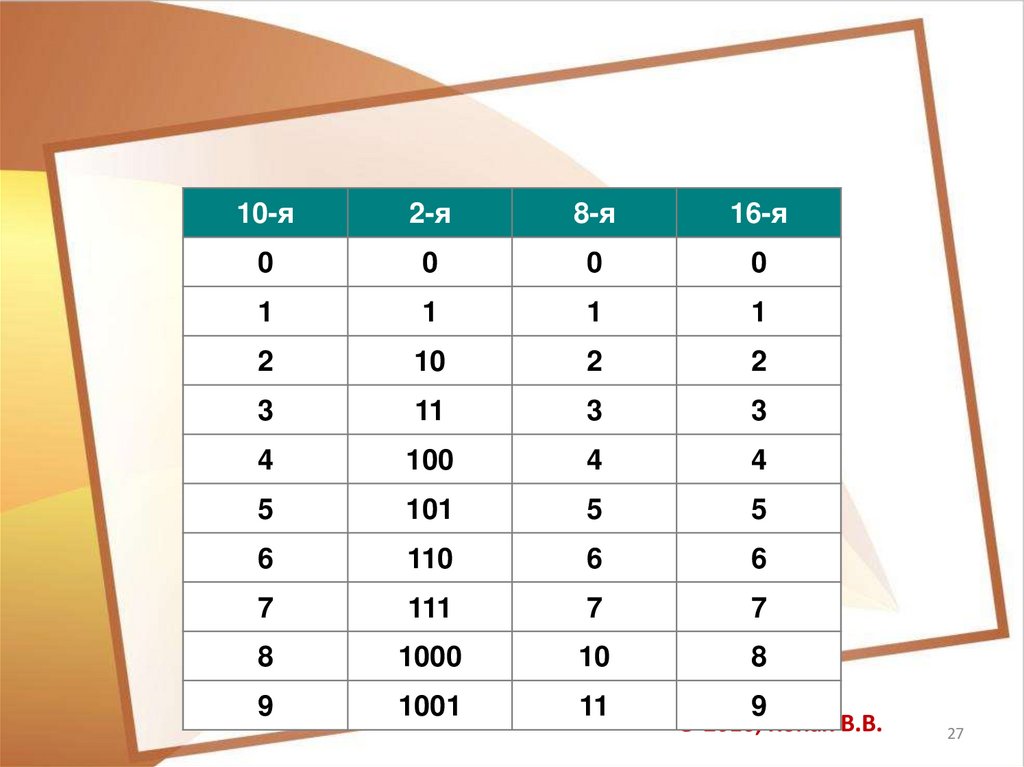
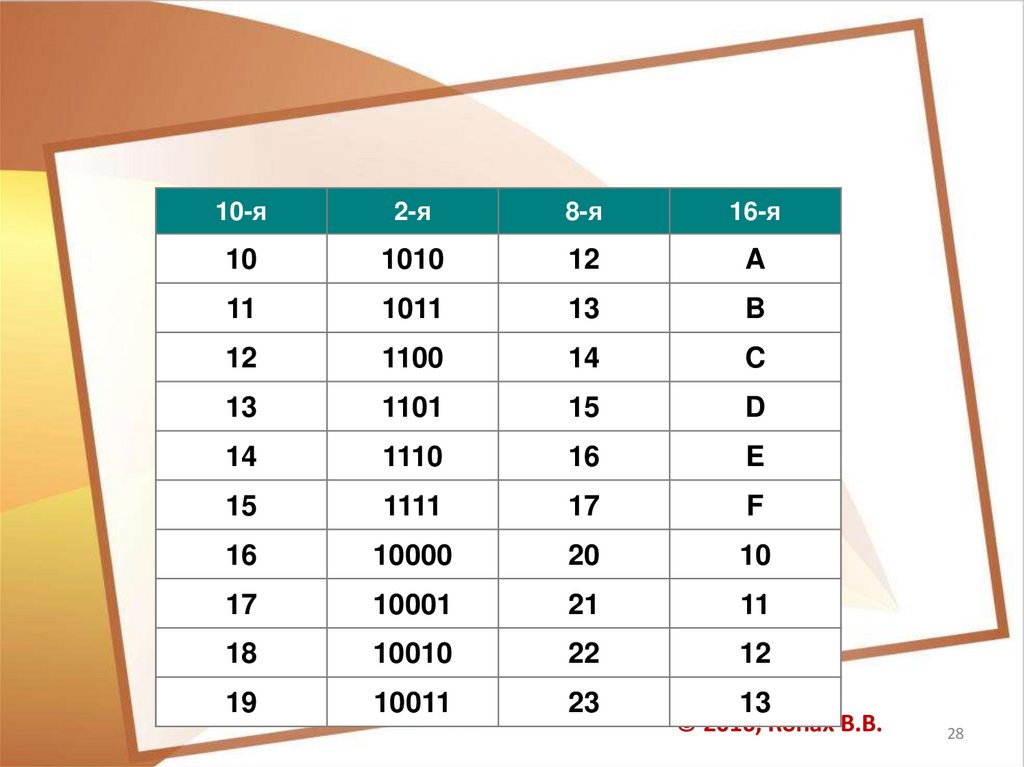
Полезно запомнить запись вэтих системах счисления
первых двух десятков целых
чисел:
© 2016, Конах В.В.
26
27.
10-я2-я
8-я
16-я
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
© 2016, Конах В.В.
27
28.
10-я2-я
8-я
16-я
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
17
10001
21
11
18
10010
22
12
19
10011
23
13
© 2016, Конах В.В.
28
29.
• Перевод восьмеричных ишестнадцатеричных чисел в двоичную
систему очень прост: достаточно
каждую цифру заменить эквивалентной
ей двоичной триадой (тройкой цифр)
или тетрадой (четверкой цифр).
© 2016, Конах В.В.
29
30.
© 2016, Конах В.В.30
31.
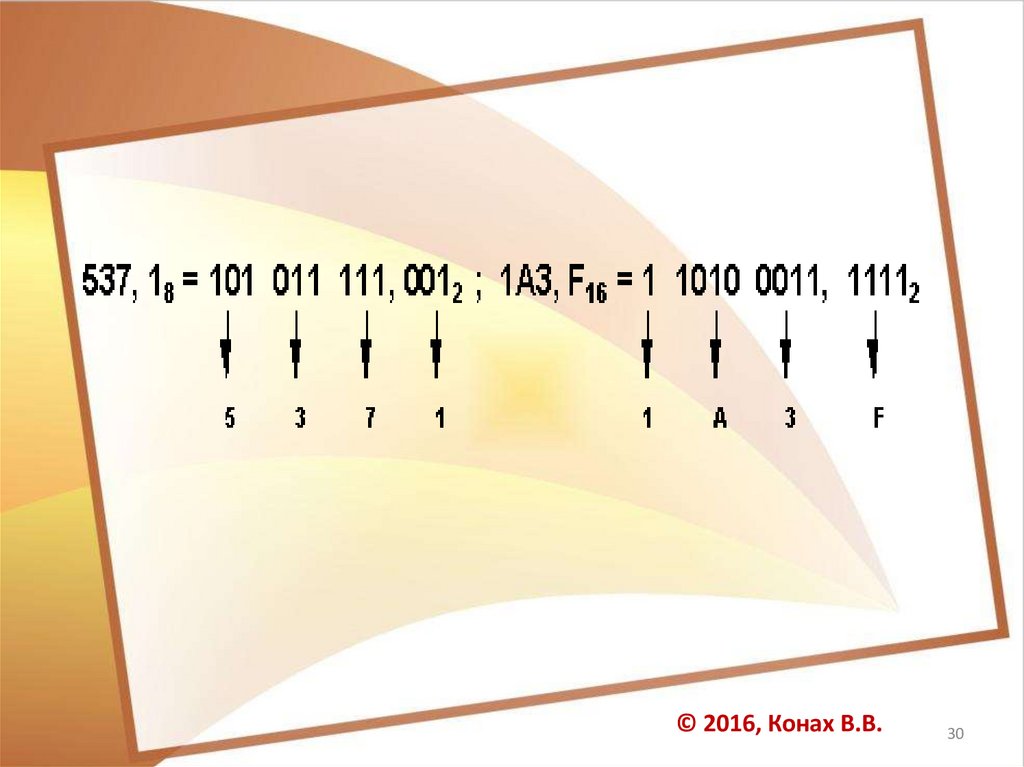
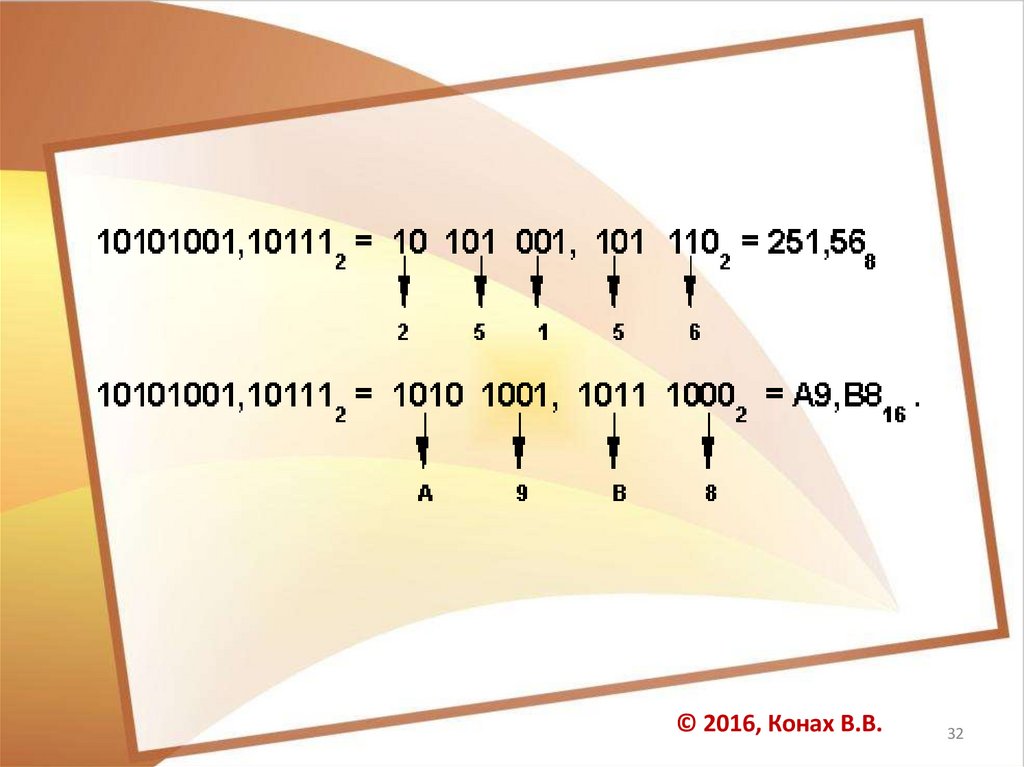
• Чтобы перевести число из двоичнойсистемы в восьмеричную или
шестнадцатеричную, его нужно разбить
влево и вправо от запятой
на триады (для восьмеричной)
или тетрады (для шестнадцатеричной) и
каждую такую группу заменить
соответствующей восьмеричной
(шестнадцатеричной) цифрой.
© 2016, Конах В.В.
31
32.
© 2016, Конах В.В.32
33.
Таблицы сложения и умножения в 2 с/с0+0=0
0*0=0
0+1=1
0*1=0
1+0=1
1*0=0
1+1=10
1*1=1
Вычислим:
10 с/с
2 с/с
5+3=8
101+11=1000
2+7=9
10+111=1001
9-5=4
1001-101=100
© 2016, Конах В.В.
33
34.
Примеры вычислений в 2 с/с111010
+ 10111
---------1010001
1.1001
- 1.0111
--------0.0010
111
х 111
--------111
111
111
--------110001
© 2016, Конах В.В.
34
35.
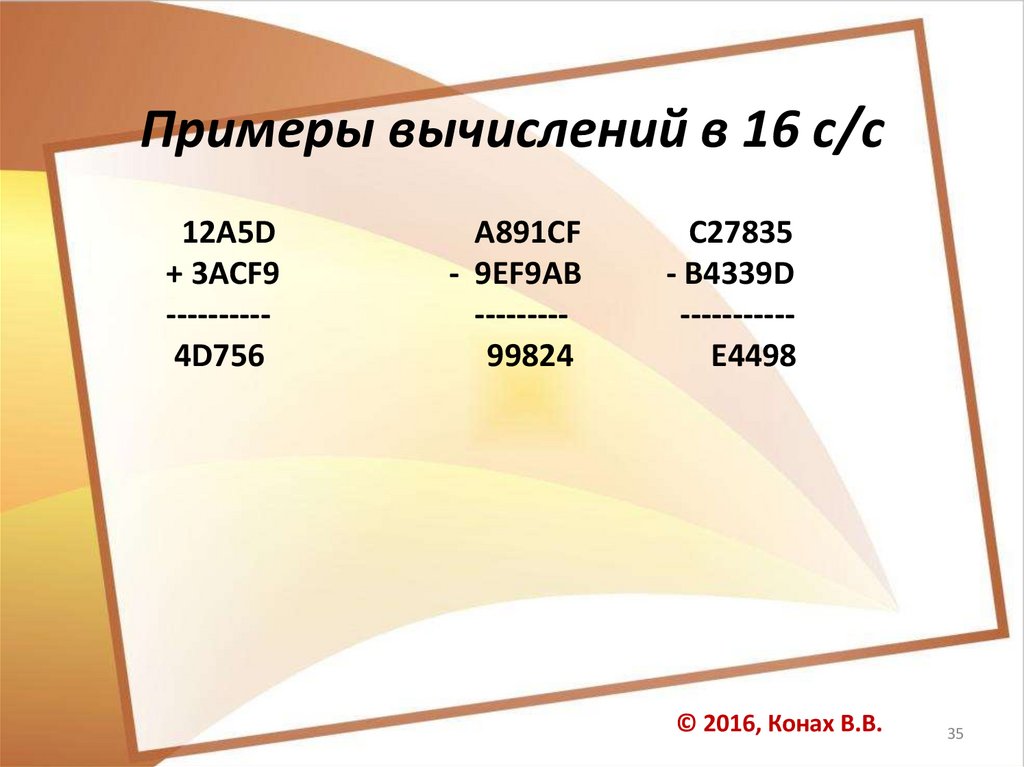
Примеры вычислений в 16 с/с12A5D
+ 3ACF9
---------4D756
A891CF
- 9EF9AB
--------99824
C27835
- B4339D
----------E4498
© 2016, Конах В.В.
35
36.
Перевод чисел из P с/с в Q с/сДля перевода целого числа N из p-ичной с/с в
систему счисления с
основанием q необходимо N разделить с остатком
("нацело") на q , записанное в той же p-ичной системе.
Затем неполное частное, полученное от такого деления,
нужно снова разделить с остатком на q , и т.д., пока
последнее полученное неполное частное не станет
равным нулю. Представлением числа N в новой
системе счисления будет последовательность остатков
деления, изображенных одной q-ичной цифрой и
записанных в порядке, обратном порядку их получения.
© 2016, Конах В.В.
36
37.
Перевод чисел из P с/с в Q с/сИли короче:
Для перевода целого числа N из p-ичной с/с
в систему счисления с
основанием q необходимо N разделить с
остатком ("нацело") на q , записанное в той же
p-ичной системе. Полученное частное снова
разделить с остатком на q , и т.д., пока это
возможно. Получаемые остатки, записанные в
обратном порядке цифрами в q-ичной с/с,
дадут запись числа N в новой системе
счисления с основанием q.
© 2016, Конах В.В.
37
38.
Перевод чисел из P с/с в Q с/сИли короче:
Для перевода целого числа N из p-ичной с/с
в систему счисления с
основанием q необходимо N разделить с
остатком ("нацело") на q , записанное в той же
p-ичной системе. Полученное частное снова
разделить с остатком на q , и т.д., пока это
возможно. Получаемые остатки, записанные в
обратном порядке цифрами в q-ичной с/с,
дадут запись числа N в новой системе
счисления с основанием q.
© 2016, Конах В.В.
38
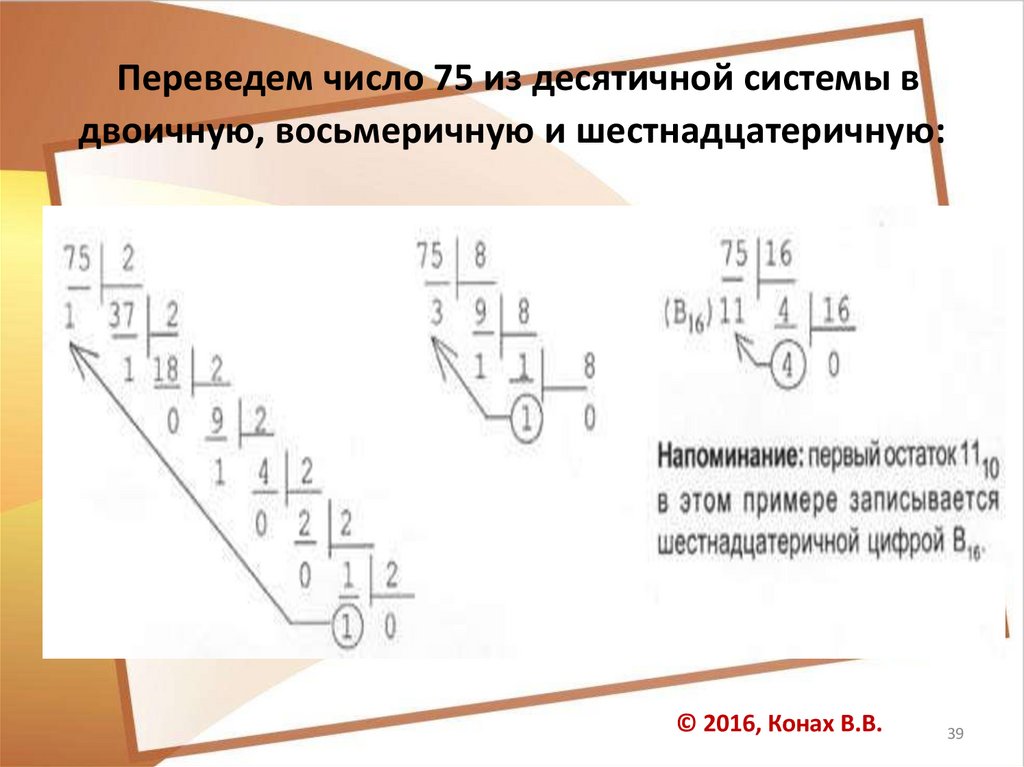
39.
Переведем число 75 из десятичной системы вдвоичную, восьмеричную и шестнадцатеричную:
© 2016, Конах В.В.
39
40.
Перевод чисел из P с/с в Q с/сДля перевода дpобной части F в с/с с
основанием q необходимо F умножить на q ,
записанное в той же десятичной системе, затем
дробную часть полученного произведения снова
умножить на q, и т. д., до тех пор, пока дpобная часть
очередного пpоизведения не станет pавной нулю,
либо не будет достигнута требуемая точность
изображения числа F в q-ичной системе.
Представлением дробной части числа F в новой
системе счисления будет последовательность целых
частей полученных произведений, записанных в
порядке их получения и изображенных одной q-ичной
цифрой.
© 2016, Конах В.В.
40
41.
Перевод чисел из P с/с в Q с/сЕсли требуемая точность перевода числа
F составляет k знаков после запятой, то
предельная абсолютная погрешность
при этом равняется q -(k+1) / 2.
© 2016, Конах В.В.
41
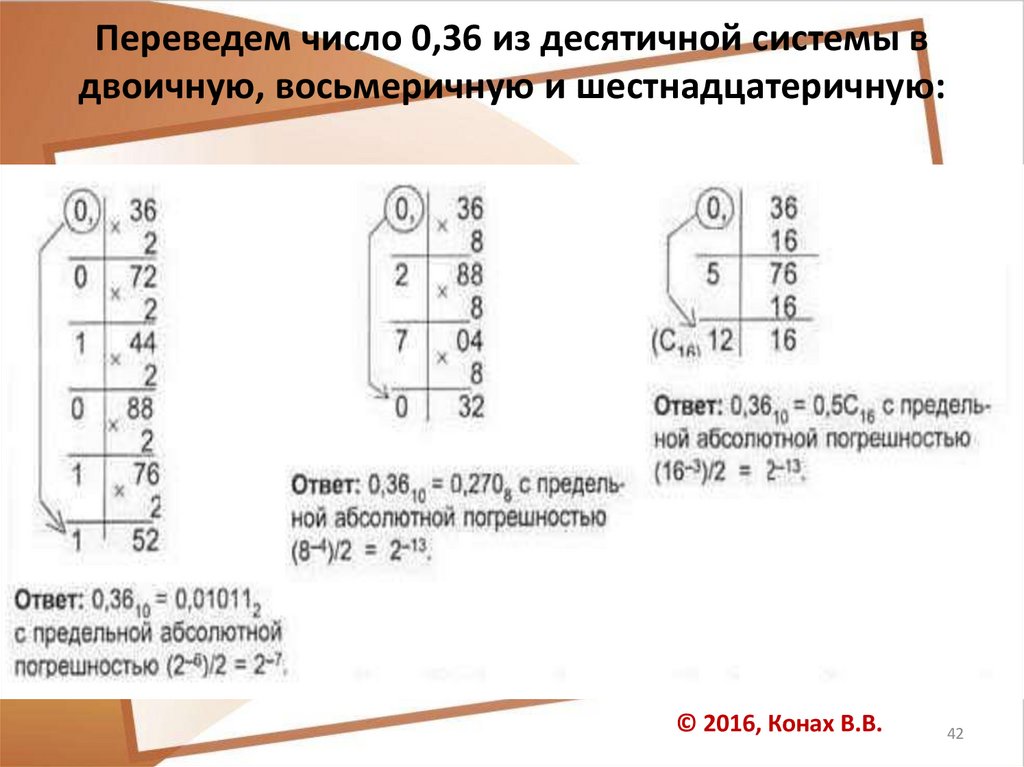
42.
Переведем число 0,36 из десятичной системы вдвоичную, восьмеричную и шестнадцатеричную:
© 2016, Конах В.В.
42
43.
Перевод чисел из P с/с в Q с/сДля чисел, имеющих как целую, так и
дробную части, перевод из десятичной
системы счисления в другую
осуществляется отдельно для целой и
дробной частей по правилам,
указанным выше.
© 2016, Конах В.В.
43
44.
Перевод чисел из Q с/с в P с/сПеревод в p-ичную систему числа x,
записанного в q-ичной cистеме счисления
в виде xq = (anan-1 ... a0 , a-1 a-2 ... a-m)q
сводится к вычислению значения
многочлена xp =
anqn +an-1qn-1+… + a0q0+ a-1q -1+a-2q-2+ …+a-mq-m
(все цифры числа и основание с/с q заменяем
их p-ичными представлениями и вычисления
выполняются в с/с с основанием p ).
© 2016, Конах В.В.
44
45.
Перевод чисел из Q с/с в P с/с© 2016, Конах В.В.
45
46.
ЗадачаВ бумагах чудака-математика была
найдена его автобиография: “Я окончил
университет 44 лет от роду. Спустя год,
100-летним молодым человеком я женился на
34-летней девушке. Разница в возрасте была
11 лет. Слустя немного лет у меня уже была
маленькая семья из 10 детей. В месяц я
получал всего 200 рублей, из которых я 1/10
часть отдавал сестре, так что мы с детьми
жили на 130 рублей в месяц.”
Чем объяснить такие странные
противоречия в цифрах?
© 2016, Конах В.В.
46
47.
Домашнее задание1. Перевести из 2с/с в 10с/с до 4-х знаков:
1001111.11001101111
111011.011011011011
1101001010.01001000011
2. Перевести из 16с/с в 10с/с до 3-х знаков:
1A7C.5A6
1BF.ACD
-4FA.3AA
© 2016, Конах В.В.
47
48.
Домашнее задание3. Перевести из 10с/с в 16с/с :
-11200.975
16389195.2175
77875.1327
32769
4. Перевести из 10с/с в 2с/с :
32.48
65.855
26.495
© 2016, Конах В.В.
48








































 informatics
informatics








