Similar presentations:
Системы счисления
1.
V. Системы счисления2.
Виды систем счисленияНепозиционная – от положения знака в изображении числа не
зависит величина, которую он обозначает.
Примером является римская система. В римской системе в качестве
цифр используется латинские буквы
I
1
V
5
X
10
L
50
C
100
D
500
M
1000
Число 32 в римской системе счисления имеет вид:
XXXII = (X+X+X)+(I+I)= 30+2
Число 444, имеющее в десятичной записи 3 одинаковые цифры, в
римской системе счисления будет записано в виде:
CDXLIV=(D-C)+(L-X)+(V-I)= 400+40+4.
Число 1974 в римской системе счисления имеет вид
MCMLXXIV= M+(M-C)+L+(X+X)+(V-I)=1000+900+50+20+4.
3.
Виды систем счисленияПозиционная – величина, обозначаемая цифрой в записи числа,
зависит от ее позиции.
Позиционную систему счисления называют традиционной,
если ее базис образует члены геометрической прогрессии, а
значения цифр есть целые неотрицательные числа. Базиспоследовательность чисел каждая из которых задает вес
соответствующего разряда.
Знаменатель P геометрической прогрессии, члены которой
образуют
базис10традиционной
счисления,
Основание
у привычной системы
десятичной
системыназывается
счисления
основанием
этой системы счисления. Традиционные системы
(десять пальцев на руках). Алфавит: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
счисления с основанием P иначе называют P-ичными.
Основание 60 придумано в Древнем Вавилоне: деление часа
В привычной нам десятичной системе значения числа образуется
на
60 минут, минуты
60 секунд,
углаумножаются
— на 360 градусов.
следующим
образом:— на
значение
цифр
на «вес»
Основание разрядов
12 распространили
англосаксы:
в году 12
соответствующих
и все полученные
значения складываются.
месяцев,
в сутках5047=5*1000+0*100+4*10+7*1.
два периода по 12 часов, в футе 12 дюймов.
Например,
Основание
5 широко
использовалось
в Китае.
Такой способ
образования
значения
числа называется
аддитивно-мультипликативным.
4.
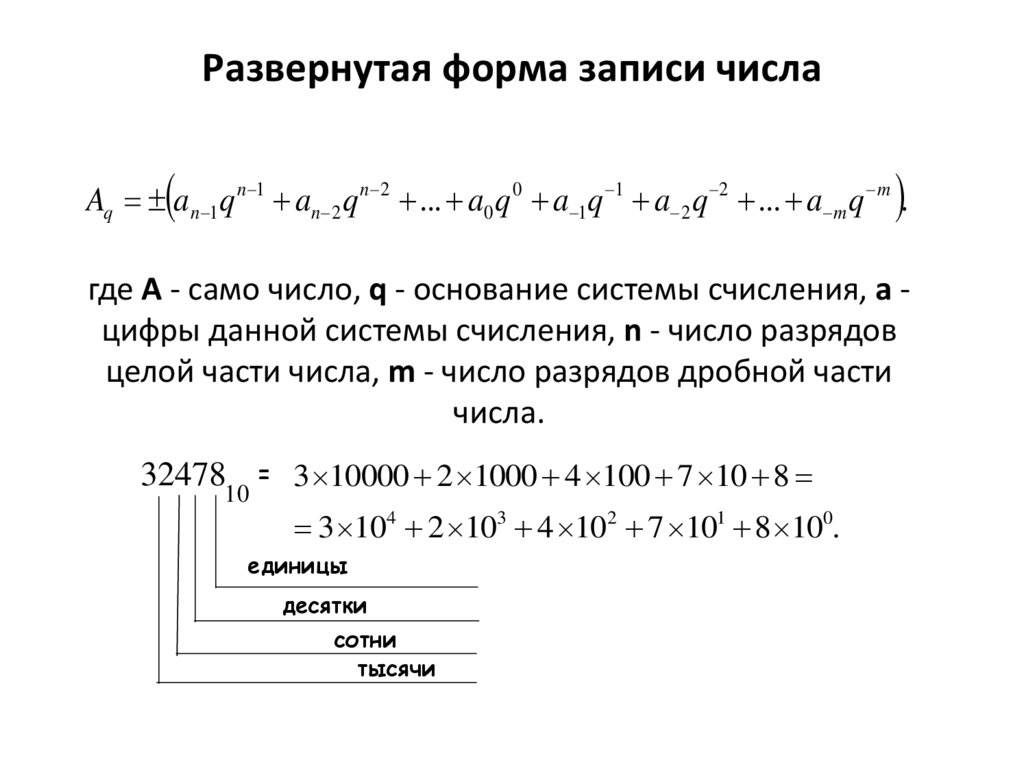
Развернутая форма записи числаAq a n 1 q n 1 an 2 q n 2 ... a0 q 0 a 1q 1 a 2 q 2 ... a m q m .
где А - само число, q - основание системы счисления, а цифры данной системы счисления, n - число разрядов
целой части числа, m - число разрядов дробной части
числа.
3247810 = 3 10000 2 1000 4 100 7 10 8
3 104 2 103 4 102 7 101 8 100.
единицы
десятки
сотни
тысячи
5.
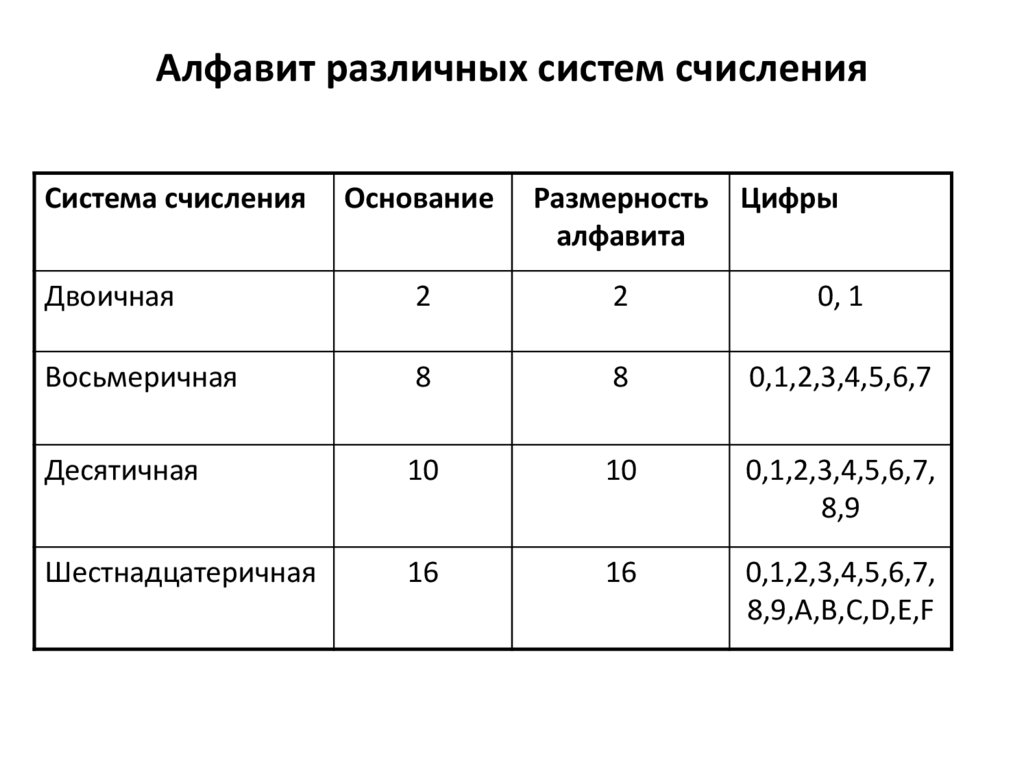
Алфавит различных систем счисленияСистема счисления
Основание
Размерность
алфавита
Цифры
Двоичная
2
2
0, 1
Восьмеричная
8
8
0,1,2,3,4,5,6,7
Десятичная
10
10
0,1,2,3,4,5,6,7,
8,9
Шестнадцатеричная
16
16
0,1,2,3,4,5,6,7,
8,9,А,В,С,D,E,F
6.
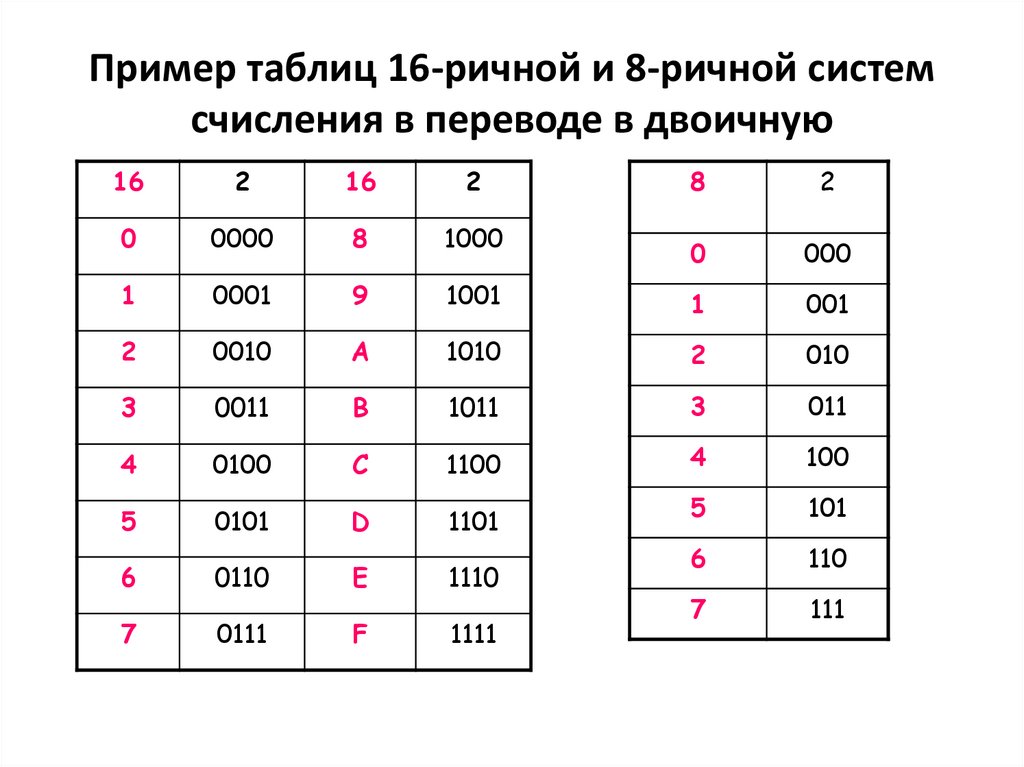
Пример таблиц 16-ричной и 8-ричной системсчисления в переводе в двоичную
16
2
16
2
8
2
0
0000
8
1000
0
000
1
0001
9
1001
1
001
2
0010
А
1010
2
010
3
0011
В
1011
3
011
4
0100
С
1100
4
100
5
0101
D
1101
5
101
6
110
7
111
6
0110
Е
1110
7
0111
F
1111
7.
Правило счета. Максимальное числоПродвижением цифры называют замену её следующей по
величине. Продвижение старшей цифры (например, цифры 9 в
десятичной системе) означает замену её на 0.
Правило счёта: для образования целого числа, следующего за
любым данным целым числом, нужно продвинуть самую правую
цифру числа; если какая-либо цифра после продвижения стала нулем,
то нужно продвинуть цифру, стоящую слева от неё.
Для записи одного и того же значения в различных системах
счисления требуется разное число позиций или разрядов:
9610(2 разряда) = 6016 (2 разряда) = 1408 (3 разряда) = 11000002 (7 разрядов)
Чем меньше основание системы, тем больше длина числа (длина
разрядной сетки). Если длина разрядной сетки задана, то это
ограничивает максимальное по абсолютному значению число, которое
можно записать.
Aq(max) = qN – 1,
где N — длина разрядной сетки (любое положительное число).
8.
Двоичная система счисленияОфициальное «рождение» двоичной системы счисления (в её алфавите
два символа: 0 и 1) связывают с именем Готфрида Вильгельма Лейбница. В
1703 г. он опубликовал статью, в которой были рассмотрены все правила
выполнения арифметических действий над двоичными числами.
Преимущества:
- для её реализации нужны технические устройства всего с
двумя устойчивыми состояниями:
есть ток // нет тока или намагничен // не намагничен;
- представление информации посредством только двух
состояний надежно и помехоустойчиво;
- возможно применение аппарата булевой алгебры для
выполнения логических преобразований информации;
- двоичная арифметика намного проще десятичной.
Недостаток:
быстрый рост числа разрядов, необходимых для записи
чисел.
232 = 429496729610 = 1000000000000000000000000000000002
9.
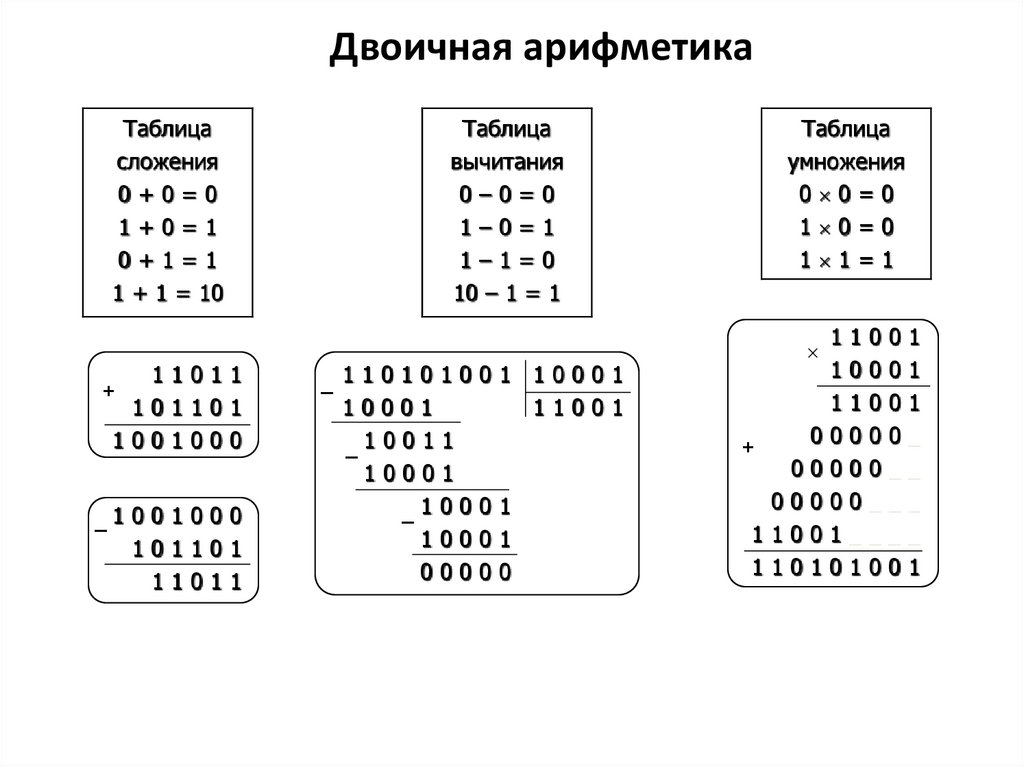
Двоичная арифметикаТаблица
сложения
0+0=0
1+0=1
0+1=1
1 + 1 = 10
11011
101101
1001000
+
1001000
–
101101
11011
Таблица
вычитания
0–0=0
1–0=1
1–1=0
10 – 1 = 1
–
1101010
10001
10011
–
10001
100
–
100
000
Таблица
умножения
0 0=0
1 0=0
1 1=1
01 10001
11001
+
01
01
00
0
00
110
110
0
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
0
0
0
_
1
0
0
0
0
0
_
_
0
0
0
0
0
_
_
_
0
1
1
1
_
_
_
_
1
10.
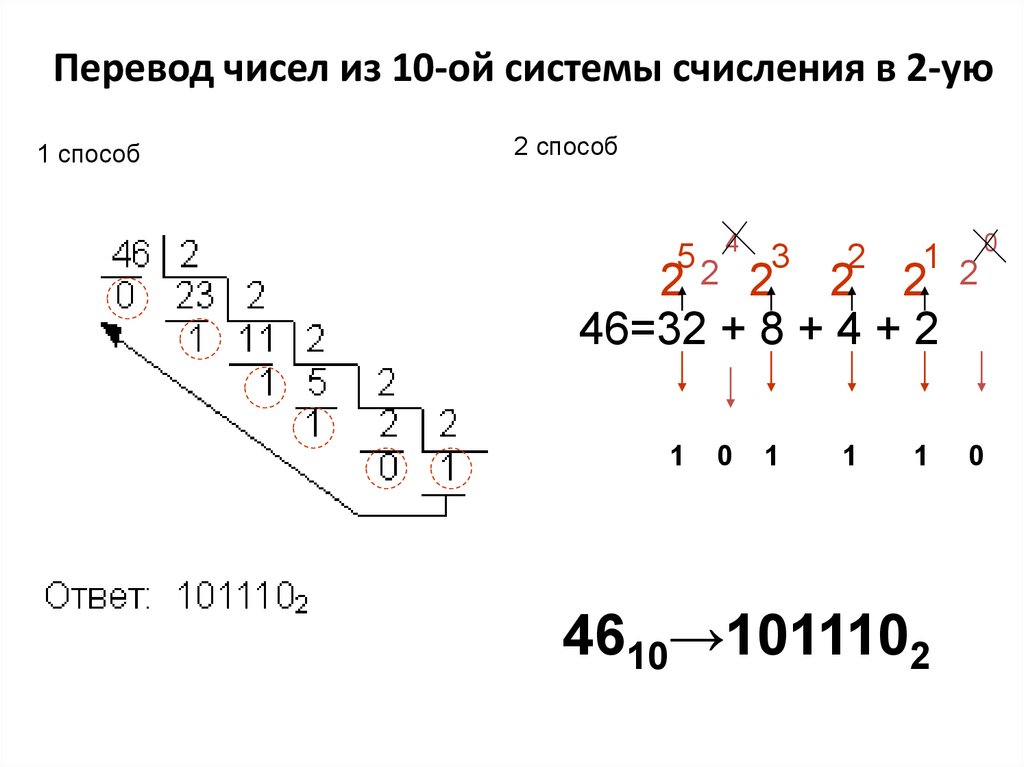
Перевод чисел из 10-ой системы счисления в 2-ую1 способ
2 способ
524 3
2
1
1
1 20
2
2 2 2
46=32 + 8 + 4 + 2
0
1
1
4610→1011102
0
11.
Перевод чисел из 10-ой системы счисления в 8-ую4610→568
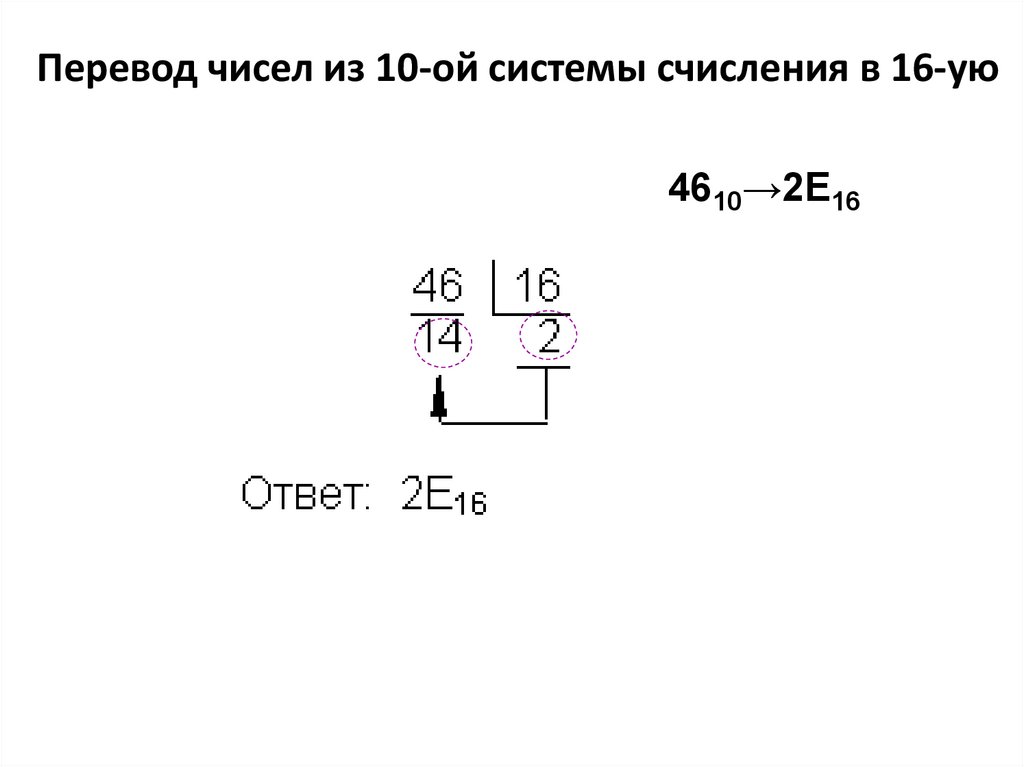
12.
Перевод чисел из 10-ой системы счисления в 16-ую4610→2E16
13.
Перевод чисел из 2-ой системы счисления в 8-уюЧтобы перевести число из двоичной системы в восьмеричную
или шестнадцатеричную, его нужно разбить влево и вправо от
запятой на триады (для восьмеричной) или тетрады (для
шестнадцатеричной)
и каждую такую группу заменить
соответствующей восьмеричной (шестнадцатеричной) цифрой.
1011102→568
14.
Перевод чисел из 2-ой системы счисления в 10-ую32
8
4
2
32+8+4+2
1011102→4610
15.
Перевод чисел из 2-ой системы счисления в 16-уюЧтобы перевести число из двоичной системы в восьмеричную
или шестнадцатеричную, его нужно разбить влево и вправо от
запятой на триады (для восьмеричной) или тетрады (для
шестнадцатеричной)
и каждую такую группу заменить
соответствующей восьмеричной (шестнадцатеричной) цифрой.
14 (E)
1011102→2E16
16.
Перевод чисел из 8-ой системы счисления в 2-ую5
6
568→1011102
17.
Перевод чисел из 8-ой системы счисления в 10-ую568→4610
18.
Перевод чисел из 8-ой системы счисления в 16-ую568→2E16
19.
Перевод чисел из 16-ой системы счисления в 2-уюПеревод восьмеричных и шестнадцатеричных чисел в двоичную
систему: каждую цифру заменить эквивалентной ей двоичной
триадой (тройкой цифр) или тетрадой (четверкой цифр).
2E16→101110 2
20.
Перевод чисел из 8-ой системы счисления в 2-уюПеревод восьмеричных и шестнадцатеричных чисел в двоичную
систему: каждую цифру заменить эквивалентной ей двоичной
триадой (тройкой цифр) или тетрадой (четверкой цифр).
568 → 1011102
21.
Перевод чисел из 16-ой системы счисления в 10-ую2E16→ 4610
22.
Перевод дробных чисел из 10-ой системы в 2-уюПеревод дробного числа из десятичной системы счисления
в двоичную осуществляется по следующему алгоритму:
1. Сначала переводится целая часть десятичной дроби в
двоичную систему счисления;
2. Затем дробная часть десятичной дроби умножается на
основание двоичной системы счисления;
3. В полученном произведении выделяется целая часть,
которая принимается в качестве значения первого после
запятой разряда числа в двоичной системе счисления;
4. Алгоритм завершается, если дробная часть полученного
произведения равна нулю или если достигнута требуемая
точность вычислений. В противном случае вычисления
продолжаются с предыдущего шага.
23.
Перевод дробных чисел из 10-ой системы в 2-ую.116 • 2 = 0.232
.232 • 2 = 0.464
.464 • 2 = 0.928
.928 • 2 = 1.856
.856 • 2 = 1.612
.612 • 2 = 1.224
Пример: Требуется перевести дробное десятичное
число 206,116 в дробное двоичное число.
Перевод целой части дает 20610=110011102 по ранее
описанным алгоритмам; дробную часть умножаем на
основание 2, занося целые части произведения в
разряды после запятой искомого дробного двоичного
числа:
.224 • 2 = 0.448
.448 • 2 = 0.456
.456 • 2 = 0.912
.912 • 2 = 1.82 и т.д.
Получим: =11001110,00011100012
24.
Перевод чисел (q) (10)Запись числа в развернутой форме и вычисление полученного
выражения в десятичной системе.
Примеры:
1101102 = 1 25 + 1 24 + 0 23 + 1 22 + 1 21 + 0 20 =
5410
2378 = 2 82 + 3 81 + 7 80 = 128 + 24 + 7 = 15910
3FA16 = 3 162 + 15 161 + 10 160 = 768 + 240 + 10 =
101810
25.
Перевод чисел (10) (q)Последовательное целочисленное деление десятичного числа
на основание системы q, пока последнее частное не станет
равным нулю.
Число в системе счисления с основанием q —
последовательность остатков деления, изображенных
одной q-ичной цифрой и записанных в порядке, обратном
порядку их получения.
Примеры:
26.
Пример смешанной системы счисленияДвоично-десятичная система счисления
100101000000100001012-10 = 9408510
Десятично-двоичная система счисления
4567810-2 = 010001010110011110002



















 informatics
informatics








