Similar presentations:
Элементы алгебры логики
1.
Саровский физико-технический институтНационального исследовательского ядерного университета МИФИ
Элементы алгебры логики
Алексеев В.В.
Саров
2016
1
2.
Понятие цифрового автомата• цифровым автоматом называется
устройство, предназначенное для
преобразования цифровой (дискретной)
информации, способное переходить под
воздействием входных сигналов из одного
состояния в другие и выдавать выходные
сигналы.
• Отличительные особенности ЦА
заключаются в том, что они имеют
дискретное множество внутренних
состояний и переход из одного в другое
осуществляется скачкообразно.
2
3.
•различают автоматы синхронного иасинхронного действия.
• Для идеализированных ЦА не
учитывается переходные процессы в
схемах и разница в фактических
величинах Т для правильного
функционирования не имеет значение.
• По степени детализации описания ЦА
различают автоматы абстрактные и
структурные. В соответствии с этим
различают абстрактную и структурную
теорию ЦА.
3
4.
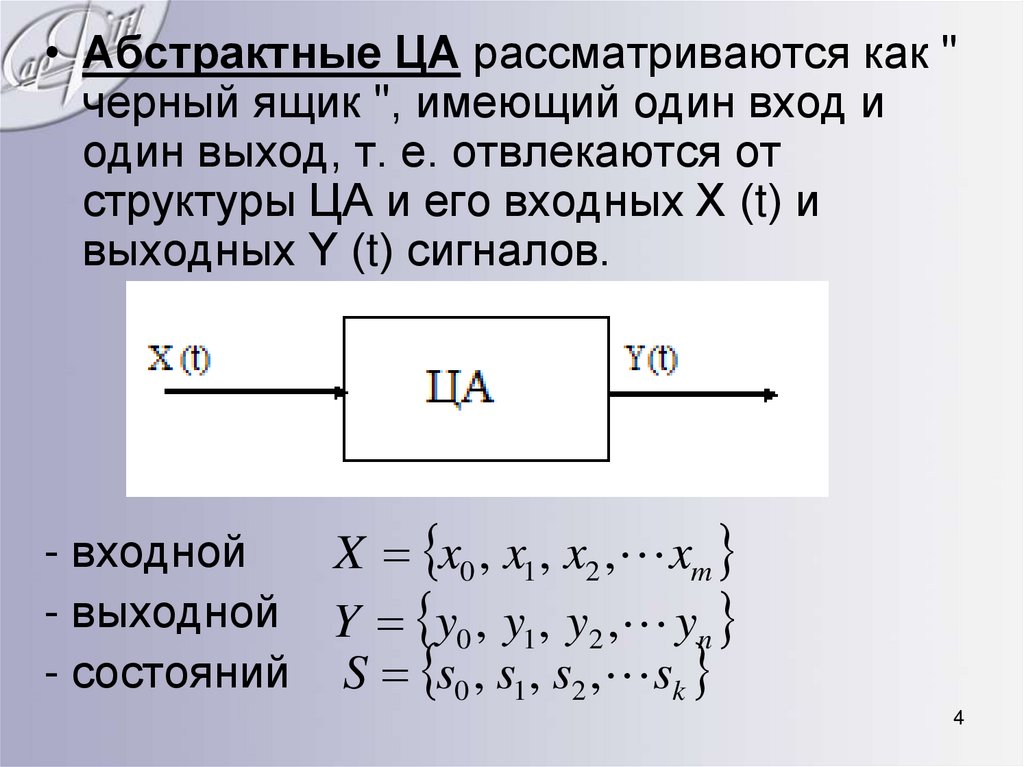
• Абстрактные ЦА рассматриваются как "черный ящик ", имеющий один вход и
один выход, т. е. отвлекаются от
структуры ЦА и его входных Х (t) и
выходных Y (t) сигналов.
- входной
X x0 , x1 , x2 , xm
- выходной Y y0 , y1 , y2 , yn
- состояний S s0 , s1 , s2 , sk
4
5.
Тогда закон функционированияабстрактного автомата может быть
задан уравнениями:
S (t 1) f [s(t ),x(t )];
Y (t ) p[x(t ),s(t )];
(1)
S (0) s0;
- где (s, x) - функция переходов
автомата ;
p (x, s) - функция выходов автомата ;
s0- начальное состояние автомата .
(Автомат Мили)
5
6.
• ЦА, выходные сигналы в которых зависяттолько от состояния автомата и не
зависят от значения входных сигналов,
называются автоматами Мура
X ( t 1) f [ s ( t ), x ( t ) ];
(2)
Y ( t ) [ s ( t ) ];
S ( 0) s0 ;
где [ s (t) ] -сдвинутая функция выхода.
6
7.
• ЦА, имеющая более одного внутреннегосостояния, называются автоматами с
памятью. Частный случай абстрактных
ЦА - автоматы с одним внутренним
состоянием. Такие тривиальные автоматы
называют автоматами без памяти или
комбинационными схемами. Закон
функционирования таких автоматов будет
определяться одним уравнением:
Y (t) = [ x(t)]
7
8.
Функции алгебры логики и ихосновные свойства.
Основные определения
1. Основное понятие АЛ - высказывание.
Высказывание - некоторое предложение,
о котором можно утверждать, что оно
истинно или ложно.
2. Логическая (Булева) переменная такая величина X, которая может
принимать только два значения:
X = { 0, 1 }.
8
9.
3. Логическая функция ( функцияалгебры логики - ФАЛ ) - функция
(x 1 , x 2 ,....x n ), принимающая значение,
равное нулю или единице на наборе
логических переменных x 1 , x 2 ,....x n .
Пусть X x1 , x2 , xn | xi Y и Y 0, 1
4. Функцией алгебры логики (ФАЛ)
называется функция, дающая
однозначное отображение X в Y, т.е.
f ( x1 , x2 , xn ) : X Y
9
10.
• 5. Если две ФАЛ f1 ( x1 x2 xn ) и f 2 ( x1 x2 xn )принимают на всех возможных наборах
значений аргументов одинаковые значения,
то функции 1 и 2 называются
равносильными (равными), т.е.:
f1 ( x1 x2 xn ) = f 2 ( x1 x2 xn )
6. Функция f ( x1 xi 1 ,xi ,xi 1 xn )
существенно зависит от аргумента , если
имеет место соотношение:
f ( x1 , xi 1 ,0, xi 1 , xn ) f ( x1 , xi 1 ,1, xi 1, xn )
10
11.
7. ФАЛ называют не полностьюопределенными или недоопределенными, если на некоторых
наборах значения ФАЛ не определены.
• Если ФАЛ не определена на m наборах
аргументов, то путем ее произвольного
доопределения можно получить 2m
различных полностью определенных
функций.
11
12.
Теорема:Число различных ФАЛ, зависящих
от
n
2n
аргументов конечно и равно 2 .
12
13.
Теорема:• Число ФАЛ, существенно зависящих от
n аргументов, определяется
следующим рекуррентным
соотношением:
An 2 C
2n
n 1
n
An 1 C
n 2
n
An 2 C A1 A0
1
n
где Аi - число ФАЛ, существенно зависящих
n!
от i аргументов, C k
n
k!( n k )!
13
14.
• Правая часть соотношения есть разностьмежду числом всех ФАЛ и суммой всех
ФАЛ, существенно зависящих от любого
числа аргументов, меньших чем n.
• Вместо рекуррентного соотношения
можно найти прямое выражение для
значений:
m
A m ( 1) C k 2
k
2 m k
k 0
14
15.
Пример:• Найти число ФАЛ, существенно
зависящих от 3-х переменных.
20
1
Имеем: A0 2 2 2.
A1 2
21
A0 4 2 2
2!
22
1
4
A 2 2 C2 A1 A 0 2
2 2 10
1!1!
A3 2
23
C 23 A 2 C13A 1 A 0 256 30 6 2 218
15
16.
Элементарные функцииалгебры логики
• n=1. Число ФАЛ равно 4:
f1 ( x) 0;
f 2 ( x) 1;
f3 ( x) x;
f 4 ( x) x.
16
17.
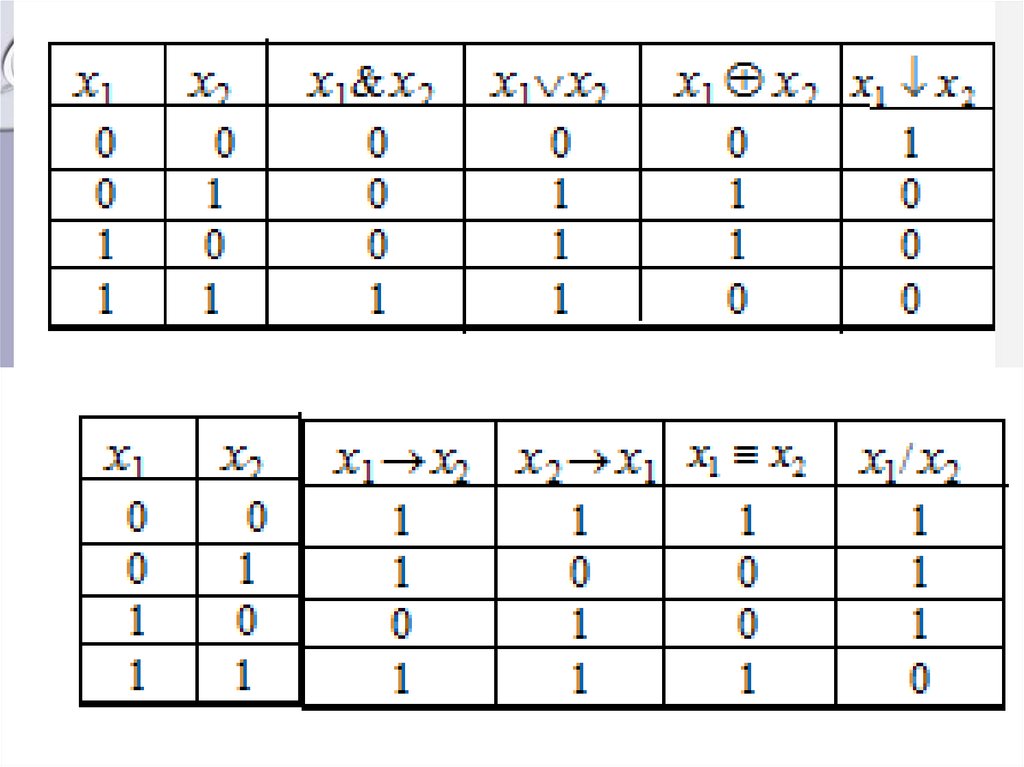
Элементарные ФАЛ 2-х переменных• n=2; Число ФАЛ равно 16.
17
18.
• имеем 10 различных функций, существеннозависящих от аргументов x1 и x2 .
18
19.
1. f ( x1 , x2 ) x1 x2 x1 & x2 x1 x2• конъюнкция (логическое умножение,
или функция И) истинна тогда и только
тогда, когда и x1 и x2 истинны.
19
20.
2. f ( x1 , x2 ) x1 x2• дизъюнкция (логическое сложение,
или функция ИЛИ) истинна тогда, и
только тогда, когда истинны или x1, или
x2, или обе переменные.
20
21.
3. f ( x1 , x2 ) x1 x2• Функция сложения по модулю 2 (или
функция разноименности, или
функция исключающее ИЛИ) истинна
тогда и только тогда когда x1 x2.
21
22.
4. f ( x1 , x2 ) x1 x2 x1 ~ x2• функция равнозначности, которая
истинна тогда и только тогда, когда обе
переменные или истинны, или ложны.
22
23.
5. f ( x1, x2 ) x1 x2• импликация х1 в х2 ложна тогда и
только тогда, когда х1 истинна, а х2
ложна
23
24.
6. f x1 x 2• функция Пирса ( Вебба ) истинна тогда
и только тогда, когда х1 и х2 ложны.
24
25.
7. f ( x1, x2 ) x1 / x2• Функция Шеффера ложна только тогда и
только тогда, когда х1и х2 истинны.
25
26.
2627.
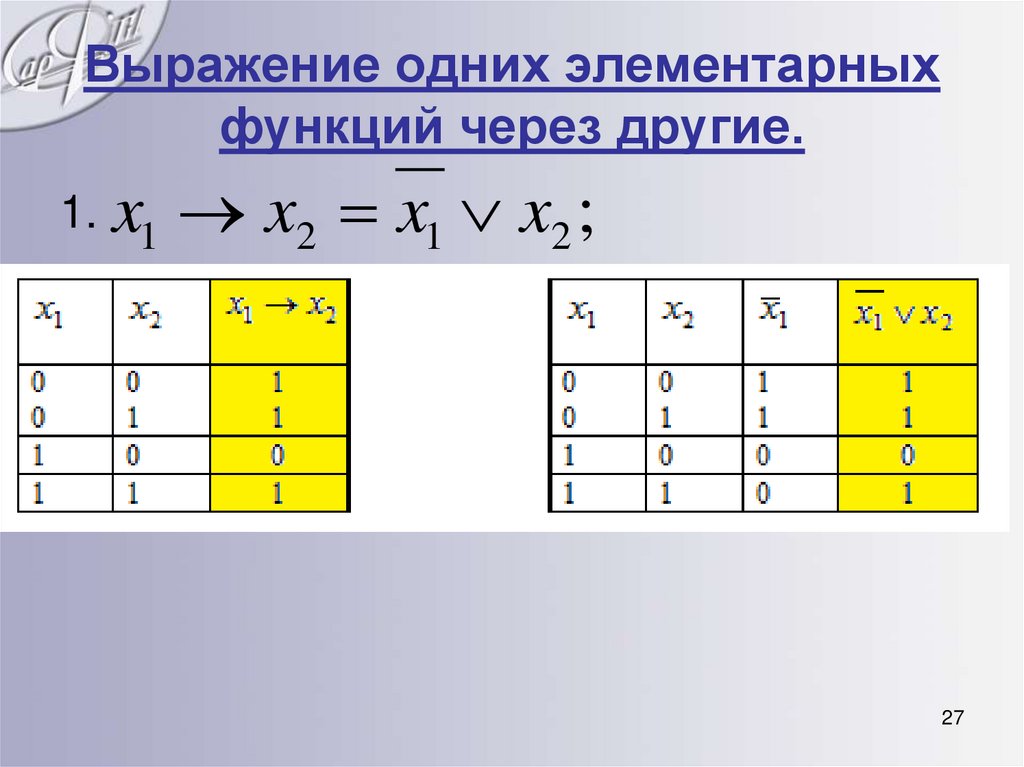
Выражение одних элементарныхфункций через другие.
1. x1 x2 x1 x2 ;
27
28.
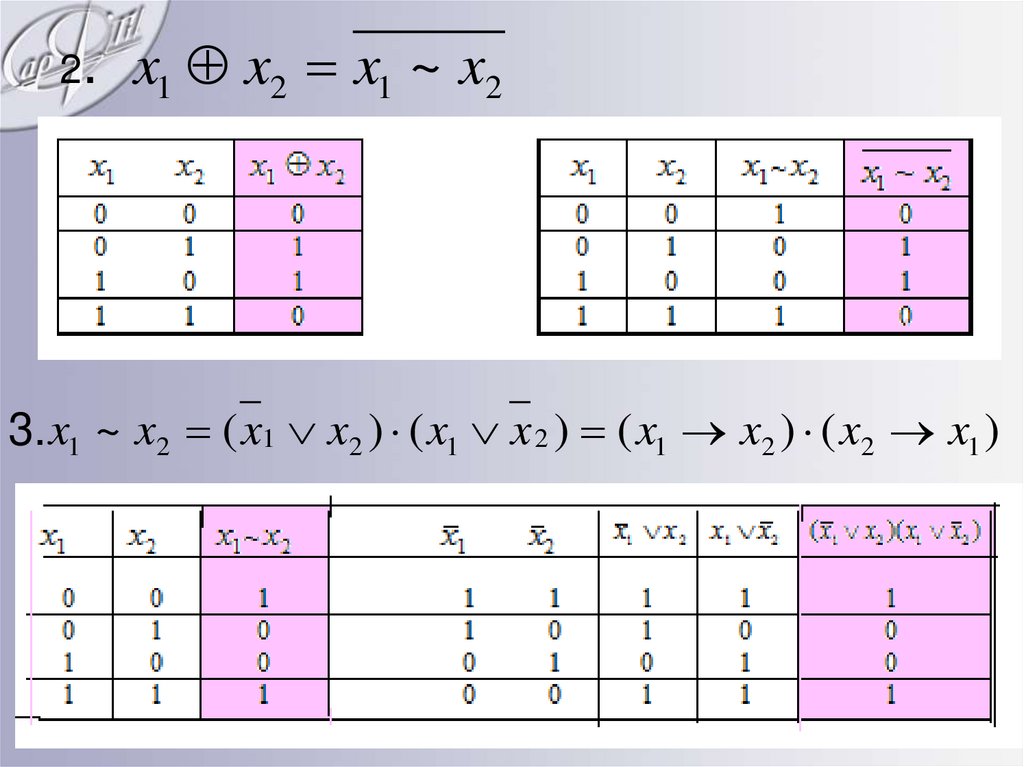
2.x1 x2 x1 ~ x2
3. x1 ~ x2 ( x1 x2 ) ( x1 x 2 ) ( x1 x2 ) ( x2 x1 )
28
29.
4. x x1 2
x1 x 2
5. x1 x2 x1 x 2
29
30.
Свойства элементарных ФАЛ.x x;
x x x;
x x x;
x x 1;
x x 0;
x 1 1;
x 0 x;
x 1 x;
x 0 0.
30
31.
Свойства конъюнкции,дизъюнкции, отрицания
1. Свойство коммутативности
(переместительный закон):
x1 x2 x2 x1
x1 x 2 x 2 x1
2. Свойство ассоциативности
(сочетательный закон):
x1 ( x2 x3 ) ( x1 x2 ) x3 ( x1 x3 ) x2
;
x1 (x 2 x 3 ) (x1 x 2 ) x 3 (x1 x 3 ) x 2
31
32.
3. Свойство дистрибутивности(распределительный закон):
• для конъюнкции относительно дизъюнкции:
x1 ( x2 x3 ) ( x1 x2 ) ( x1 x3 )
• для дизъюнкции относительно конъюнкции:
x1 x2 x3 ( x1 x2 ) ( x1 x3 )
Действительно:
32
33.
( x1 x2 ) ( x1 x3 )x1 x1 x1 x3 x2 x1 x2 x3
x1 x1 x3 x1 x2 x2 x3
x1 (1 x3 x2 ) x2 x3 x1 x2 x3
33
34.
Законы Де-Моргана:x x2 x3 xn
1. 1
x1 x2 x3 x n
x1 x2 x3 xn
2.
x1 x2 x3 xn
34
35.
Законы (правила) поглощения:1.
x1 x1 x 2 x1
2.
x1 ( x1 x 2 ) x1
x1 x1 x 2 x1 (1 x 2 ) x1 1 x1
x1 ( x1 x2 ) x1 x1 x1 x2
x1 x1 x2 x1 (1 x2 ) x1
35
36.
Из логических функцийустанавливается
• правило склеивания:
x1 x2 x1 x2 x1
• правило вычеркивания:
x1 x1 x 2 x1 x 2
36
37.
x1 x1 x2 x1 1 x1 x2x1 ( x2 x2 ) x1 x2
x1 x2 x1 x2 x1 x2
(x1 x2 x1 x2 ) ( x1 x2 x1 x2 )
x1 ( x2 x2 ) x2 ( x1 x1 )
x1 1 x2 1 x1 x2 .
37
38.
• Знание свойств, законов иправил элементарных ФАЛ
необходимо для аналитического
описания функций алгебры
логики, их преобразований.
38
39.
Свойства функции сложенияпо модулю два
x1 x2 x1 x2 ( x1 x2 ) ( x1 x2 )
( x1 x2 ) ( x1 x2 )
x1 x2 x1 x2 ( x1 x2 ) ( x1 x2 )
Функция сложения по модулю два
обладает следующими свойствами:
коммутативности (переместительный
закон)
1
2
2
1
x x x x
39
40.
ассоциативности (сочетательный закон):
x1 (x 2 x 3 ) (x1 x 2 ) x 3
дистрибутивности (распределительный
закон):
x1 ( x 2 x 3 ) x1 x 2 x1 x 3
справедливы правила:
x x 0
x x 1
x 0 x
x 1 x
40
41.
• Функции НЕ, ИЛИ, НЕ могут бытьвыражены через функцию сложения по
модулю два следующим образом:
x x 1
x1 x 2 x1 x 2 x1 x 2
x1 x 2 ( x1 x 2 ) ( x1 x 2 )
41
42.
Свойства функции импликацииx 1 x 2 x1 x 2
• Для функции импликации справедливы
следующие правила:
• x x 1
x 0 x
x x x
x 1 1
0 x 1
1→




























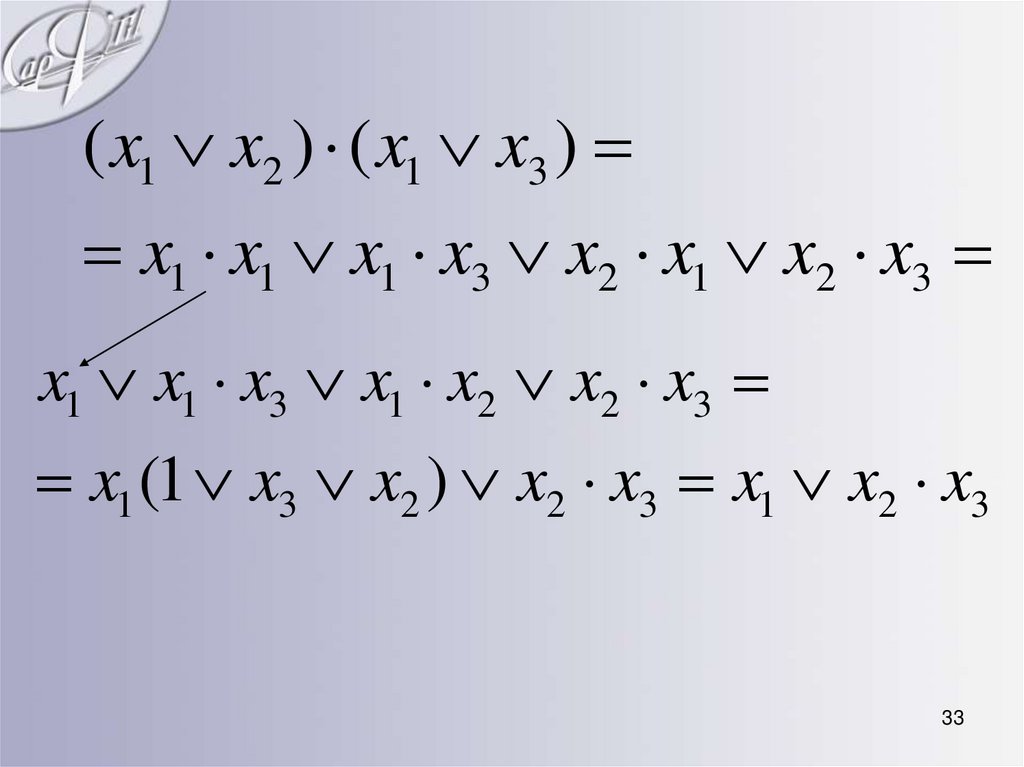



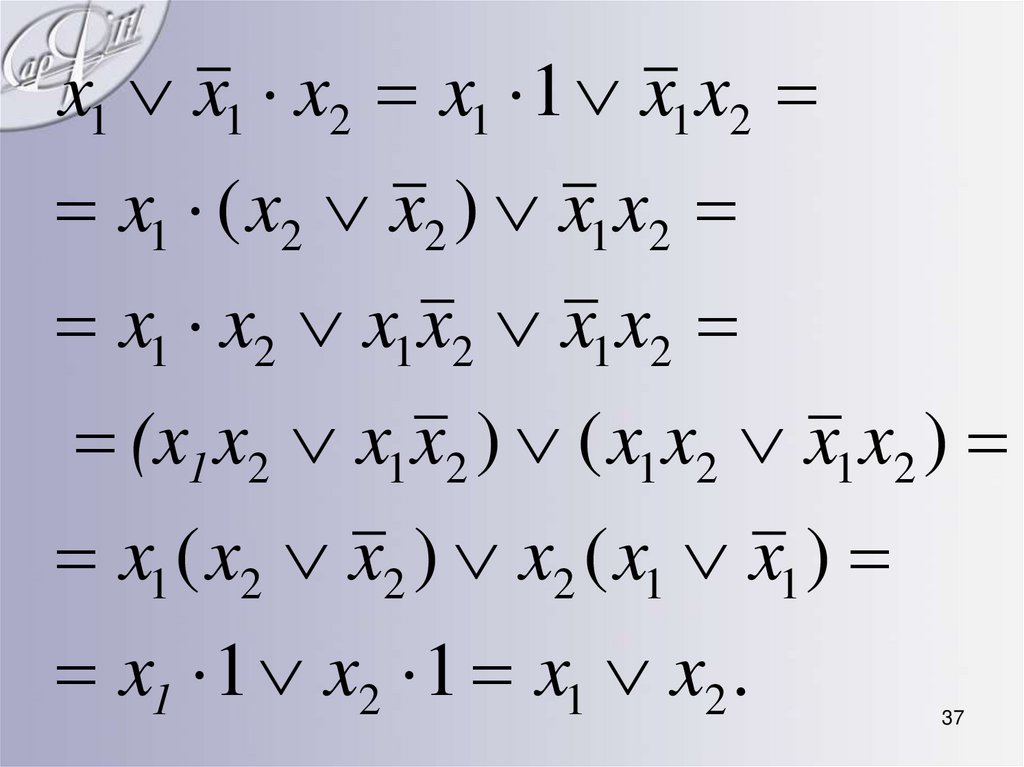






























 mathematics
mathematics








