Центр тяжести

1.

Центр тяжести
АНАЯТОВ АЛЕКСЕЙ ЕВГЕНЬЕВИЧ

2.

Центр параллельных сил
Центр параллельных сил это точка, при повороте вокруг которой всех сил системы на один
и тот же угол, линия действия равнодействующей системы параллельных сил повернется в
ту же сторону на тот же угол.

3.

Центр тяжести
Центром тяжести называется геометрическая точка, жестко связанная с телом, и
являющаяся центром параллельных сил тяжести, приложенных к отдельным
элементарным частицам этого тела
Для однородного тела положение центра тяжести тела не зависит от материала, а
определяется геометрической формой тела.

4.

Как найти центр тяжести?
Проецируя на оси и переходя к пределу, выводим формулы координат центра тяжести
однородного твердого тела объемом V

5.

Способы определения координат
центра тяжести
1. Аналитический (путем интегрирования).
2. Метод симметрии. Если тело имеет плоскость, ось или центр
симметрии, то его центр тяжести лежит соответственно в плоскости
симметрии, оси симметрии или в центре симметрии.
3. Экспериментальный. (метод подвешивания тела).
4. Разбиение. Тело или фигура разбивается на конечное число частей
(простых тел или фигур), для каждой из которых положение центра
тяжести C и площадь A известны.
5. Дополнение (Метод отрицательных площадей или объемов)

6.

Ix, Wx
Момент инерции отвечает за то, насколько трудно крутить предметы.
Пример: крутить велосипедное колесо.
Момент сопротивления отвечает за прочность предметов под нагрузкой.
Пример: мост, который должен выдерживать вес машин.

7.

Прямоугольник
Центр тяжести прямоугольника расположен в точке пересечения его диагоналей, на
расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали

8.

Квадрат
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a

9.

Треугольник равнобедренный
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии
1/3 высоты от основания и 2/3 высоты от его вершин

10.

Прямоугольный треугольник
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении
медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.

11.

Трапеция
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте,
определяемой по формуле

12.

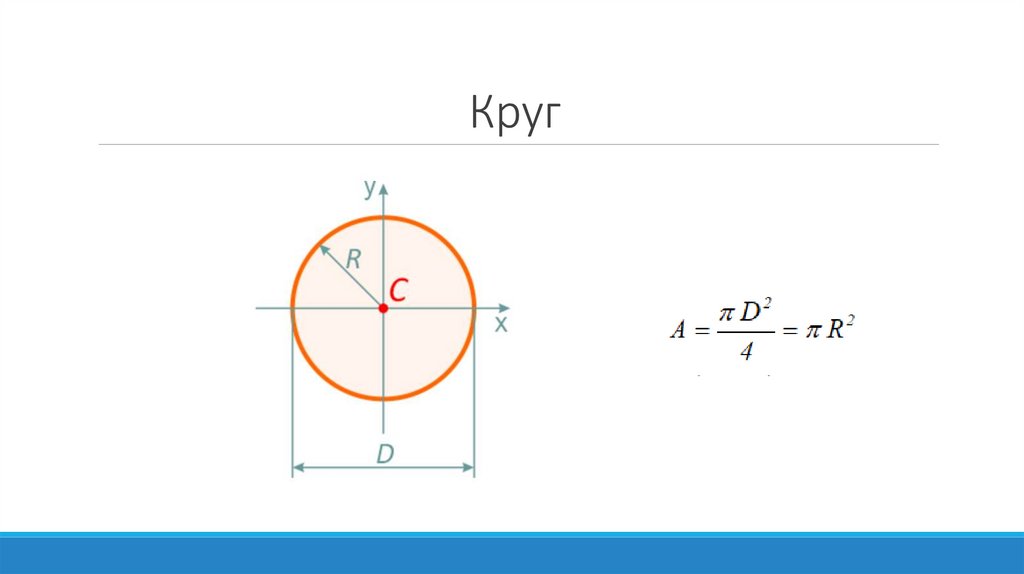
Круг

13.

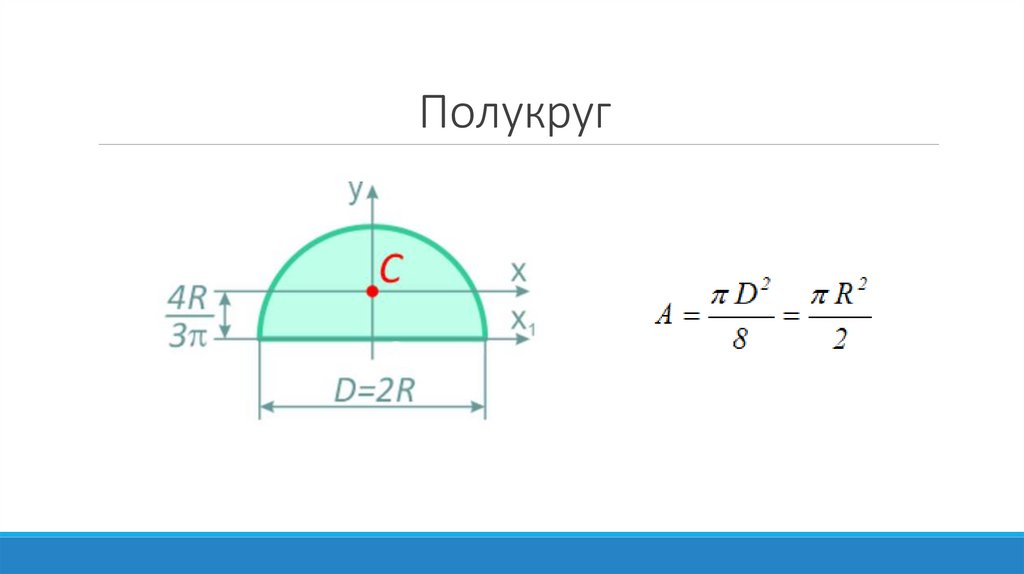
Полукруг

14.

Четверть круга

15.

Кольцо
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.

16.

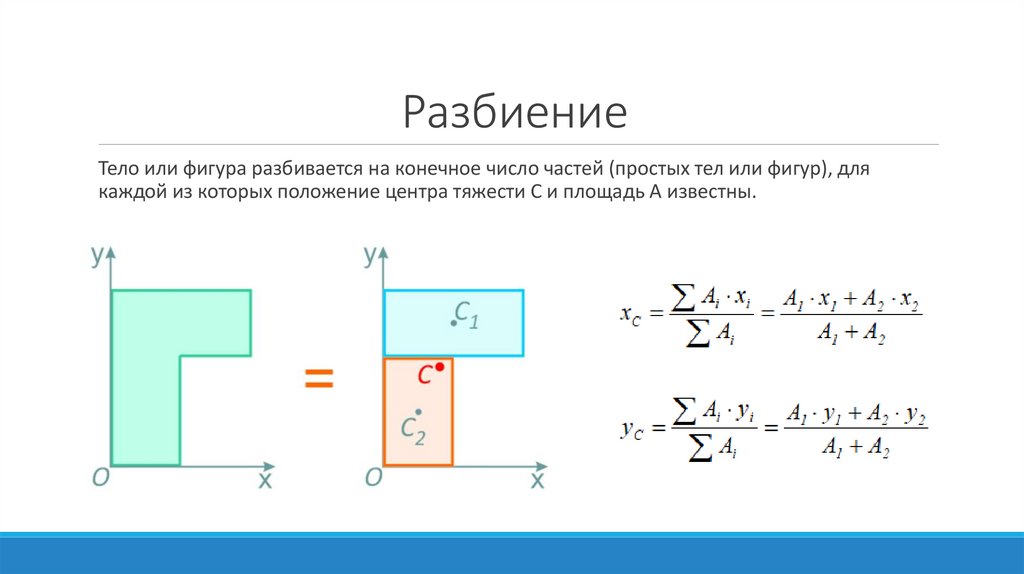
Разбиение
Тело или фигура разбивается на конечное число частей (простых тел или фигур), для
каждой из которых положение центра тяжести C и площадь A известны.

17.

Дополнение
Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим
вырезы, если центры тяжести тела без выреза и вырезанной части известны