Слайд-лекция «Дифференциальные уравнения высших порядков»

1. 6B07102 Машиностроение 6B07107 Химическая технология неорганических веществ 6B07305 Инженерные системы и сети 6B11301

Дисциплина: «Математика 2»
Слайд-лекция «Дифференциальные уравнения высших
порядков»
6B07102 МАШИНОСТРОЕНИЕ
6B07107 ХИМИЧЕСКАЯ ТЕХНОЛОГИЯ НЕОРГАНИЧЕСКИХ ВЕЩЕСТВ
6B07305 ИНЖЕНЕРНЫЕ СИСТЕМЫ И СЕТИ
6B11301 ОРГАНИЗАЦИЯ ПЕРЕВОЗОК, ДВИЖЕНИЯ И ЭКСПЛУАТАЦИЯ ТРАНСПОРТА
6B07202 МЕТАЛЛУРГИЯ
6B07205 МЕТАЛЛУРГИЯ
6B07110 ТЕХНОЛОГИЧЕСКИЕ МАШИНЫ И ОБОРУДОВАНИЕ (ПО ОТРАСЛЯМ)
6B07103 ТРАНСПОРТ, ТРАНСПОРТНАЯ ТЕХНИКА И ТЕХНОЛОГИИ
6B07302 СТРОИТЕЛЬСТВО
6B07501 СТАНДАРТИЗАЦИЯ, СЕРТИФИКАЦИЯ И МЕТРОЛОГИЯ (ПО ОТРАСЛЯМ)
.

2.

ДУ n –го порядка имеет вид:
F ( x, y, y ,... y ) 0
( n)

3.

Если такое уравнение разрешимо относительно
старшей производной, то оно имеет вид:
y
(n)
f ( x, y, y ,..., y
( n 1)
)
Решением такого уравнения будет функция у(х),
которая обращает его в тождество.

4.

Для удобства вместо одного ДУ n – го порядка
рассматривают систему из n ДУ первого
порядка.
dy
y1 ;
dx
dyn 2
dy1
y2 ; ...;
yn 1
dx
dx
Поэтому
y
(n)
dy n 1
dx

5.

Тогда можно записать:
dyn 1
f ( x, y, y1 ,... yn 1 )
dx
Это система n ДУ с n неизвестными функциями
y, y1 ,... yn 1
Система, в которой слева стоят производные от
искомых функций, а справа – функции от
независимой переменной и искомой функции,
называется системой n ДУ первого порядка
нормальной формы.

6.

Обобщим эту систему:
dy1
dx f1 ( x, y, y1 ,... yn )
dy
2 f 2 ( x, y, y1 ,... yn )
dx
...
dyn
f n ( x, y, y1 ,... yn )
dx
1

7.

Пусть для системы (1) выполняются
следующие условия:
1
Функции fi непрерывны по всем аргументам
в области D.

8.

2
Частные производные
df i
dyk
непрерывны в области D.

9.

Тогда существует одна и только одна
система решений уравнений (1):
y1 y1 ( x),
y2 y2 ( x), ... yn yn ( x)
определенная в некоторой окрестности
точки х0 и удовлетворяющая при х=х0
заданным условиям:
y y1 ( x0 ), y2 y2 ( x0 ), ... yn yn ( x0 )
0
1
0
0

10.

Теорема Коши утверждает существование частного
решения системы (1).
Геометрически это означает, что существует
единственная интегральная кривая, проходящая
через точку
0
1
0
( x0 , y ,..., yn )

11.

Уравнение
y ( n ) f ( x, y, y ,..., y ( n 1) )
правая часть которого непрерывна по всем
аргументам и дифференцируема по ним в
некоторой замкнутой области D, имеет
единственное решение, удовлетворяющее
начальным условиям при х=х0 :

12.

x x0 , y y0 , y y0 , ... y
где
( n 1)
( n 1)
x0 , y0 , y0 , ..., y0
- заданные числа.
y ( x, C1 , C2 ,..., Cn )
y
( n 1)
0

13.

Уравнение вида
F ( x, y, y , y ) 0
называется ДУ второго порядка.
где х – независимая переменная;
у– неизвестная функция;
у' и у"– ее первая и вторая производные.

14.

Будем рассматривать уравнения второго порядка,
разрешенные относительно второй производной:
y f ( x, y, y )
6
Решением ДУ второго порядка называется
функция у=φ(х), определенная на
некотором интервале (a,b), которая
при подстановке ее в уравнение
обращает его в тождество.

15.

Пусть дано ДУ (6). Если функция f(x,y,у') и ее
частные производные f'y и f'y' непрерывны
в некоторой области D пространства
переменных (х,у,у'), то для любой
внутренней точки (х0,у0,у'0) этой области
существует единственное решение
уравнения, удовлетворяющее начальным
условиям х=х0, у=у0, у‘=у'0

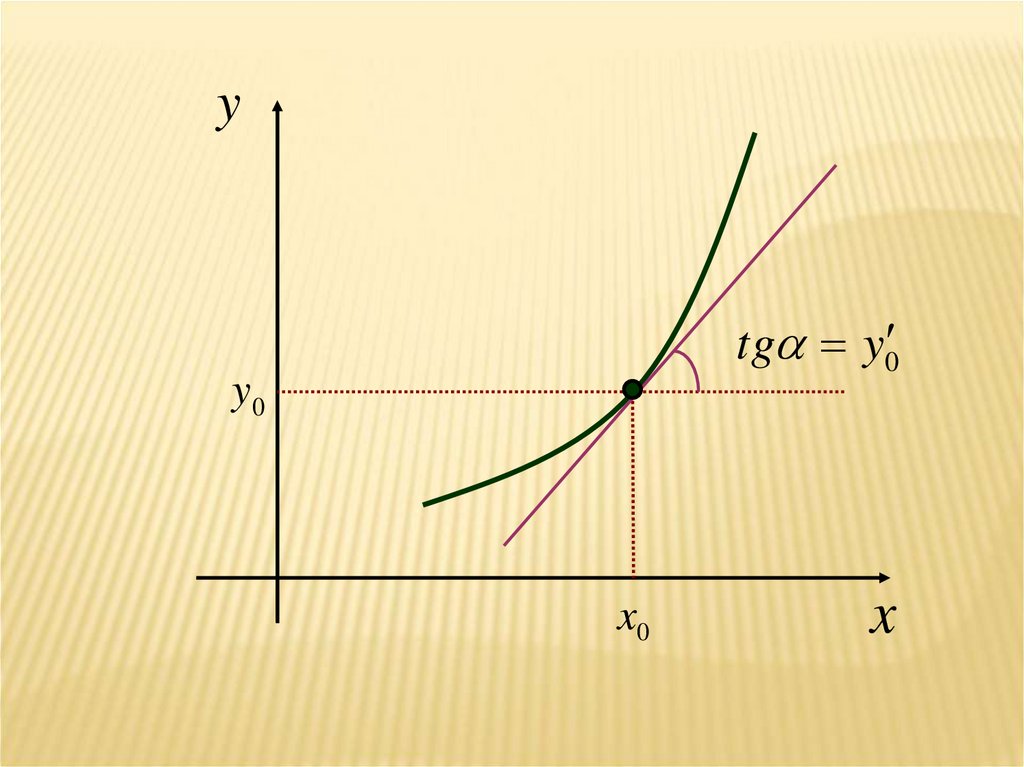
16.

Через заданную точку (х0 ,у0 ) на плоскости ХОУ
проходит единственная интегральная кривая с
заданным значением углового коэффициента
касательной у0' .

17.

y
tg y0
y0
x0
x

18.

Общим решением уравнения (6) в некоторой
области D называется функция
y ( x, C1 , C2 )
удовлетворяющая
этому
уравнению
произвольных значениях С1 и С2.
при
Частным решением уравнения (6) называется
общее решение, взятое при фиксированных
значениях этих постоянных:
y ( x, C , C )
1
0
2
0

19.

Рассмотрим уравнение
y 0
Его общее решение получается при двукратном
интегрировании:
2
d y
0
y
dy
dx
0
y
C1
2
dx
dy
C1 dy C1 dx dy C1 dx
dx

20.

y C1 x C2
Найдем частное решение уравнения при
y x 1 2 y x 1 1
Подставляем в общее решение:
C1 1
2 C1 C2
C1 1
C2 1
Частное решение будет иметь вид:
y x 1

21.

Существуют три вида уравнений второго порядка,
допускающих понижение степени.
1
Уравнения вида
y f (x )

22.

Введем новую функцию:
z ( x) y
Тогда исходное уравнение станет
уравнением первого порядка:
неполным
z f (x)
Его решение:
dz
f ( x) dz f ( x)dx z f ( x)dx C1
dx

23.

Возвращаемся к старой переменной:
y f ( x)dx C1
y f ( x)dx C1 dx
y f ( x)dx dx C1 x C2
Рассмотренный в предыдущем параграфе пример
относится к этому случаю.

24.

2
Уравнения вида y f ( x, y )

25.

Введем новую функцию:
z ( x) y
Находим общее решение этого уравнения:
z ( x, C1 )
Затем проинтегрируем его и найдем общее решение
исходного уравнения:
y ( x) ( x, C1 )dx C2

26.

Решить дифференциальное уравнение:
x y y 0

27.

В это уравнение явно не входит у. Делаем замену:
z ( x) y
x z z 0
Разделяем переменные:
dz
x z 0
dz
dz
dx
z x
dz
z
dz
x
dz
dx
z
x
ln z ln x C1

28.

z e
ln x C1
e
ln x
e C2 e
C1
ln
1
x
1
C2
x
1
z C2
x
Возвращаемся к старой переменной:
dy
1
C2
z C2
dy dx
dx
x
x
y C2 ln x C3
C2
dy x dx

29.

3
Уравнения вида y f ( y, y )

30.

Введем новую функцию:
z ( y ) y
По
правилу
функции:
дифференцирования
сложной
d
dz
dz
y z ( y ) y z
dx
dy
dy
Тогда исходное уравнение преобразуется в ДУ
первого порядка относительно функции z(y):
dz
z f ( y, z )
dy

31.

Пусть общее решение этого уравнения
z ( y, C1 )
Тогда обратной заменой получаем неполное
уравнение первого порядка относительно у(х):
dy
( y, C1 )
dx
Решаем его методом разделения переменных:
dy
( y, C1 ) x C2
Отсюда находим искомую функцию у=у(х).

32.

Решить дифференциальное уравнение:
y ( y ) 0
2

33.

В это уравнение явно не входит х. Делаем замену:
z ( y ) y
dz
y
z
dy
dz
z
dy
Первое решение этого уравнения:
z 0
y C1
dz
2
z z 0
dy

34.

dz
z dy ln z y C2
y C2
C2
y
y
z e
e e C3 e
z C3 e y C4 e y
Возвращаемся к старой переменной:
dy
C4 e y
dx
e
y
dy
dx
y
C4 e
C4 x C5
e
y
dy
e y C4 dx
(C4 x C5 )
y( x) ln( C4 x C5 )