Теория графов. Введение. История возникновения

1.

Теория графов
Лектор: доцент кафедры ПМ
Спиридонова Е.В.

2.

План лекции
1. Введение. История возникновения
2. Основные понятия и определения
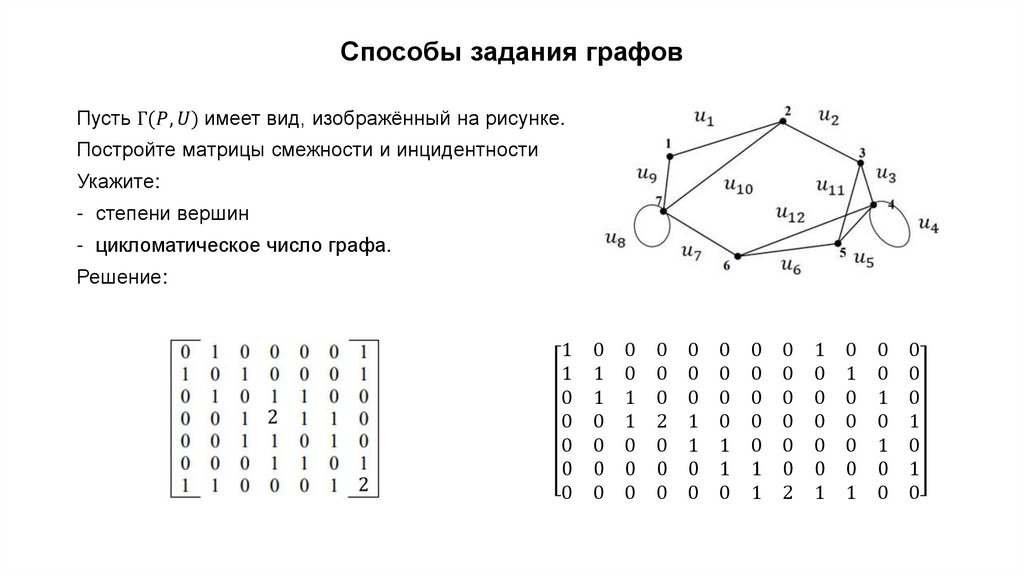
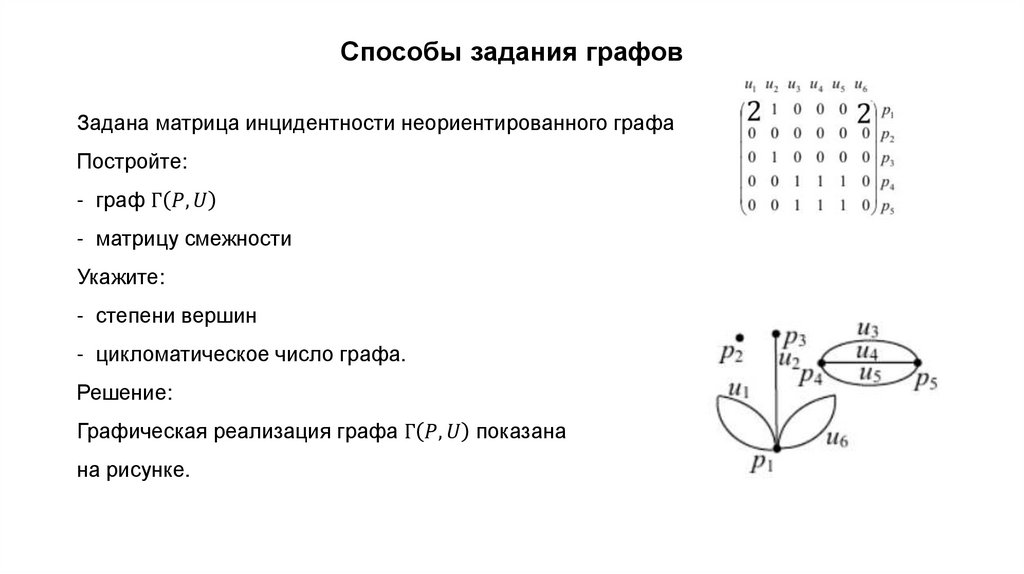
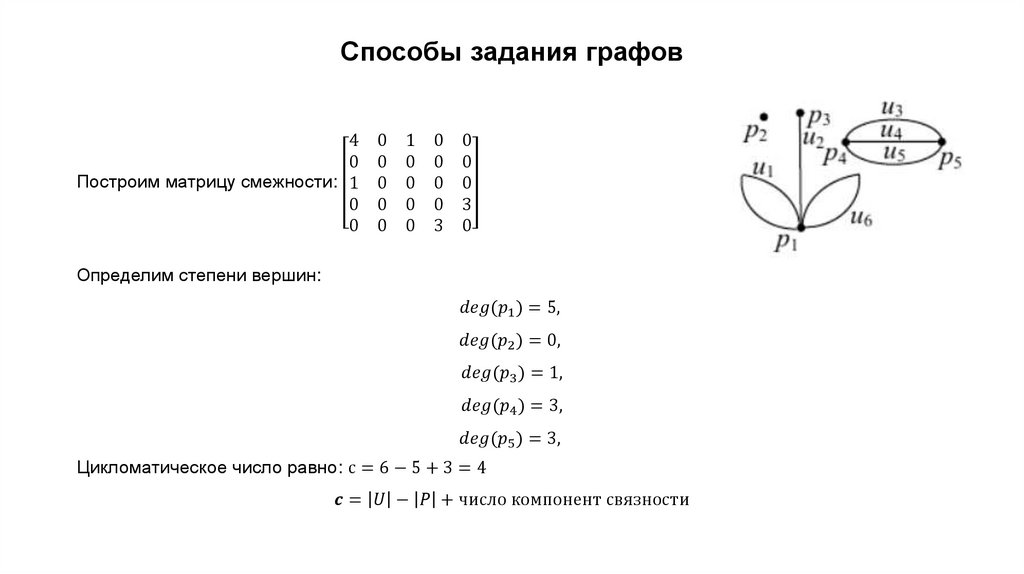
3. Способы задания графов
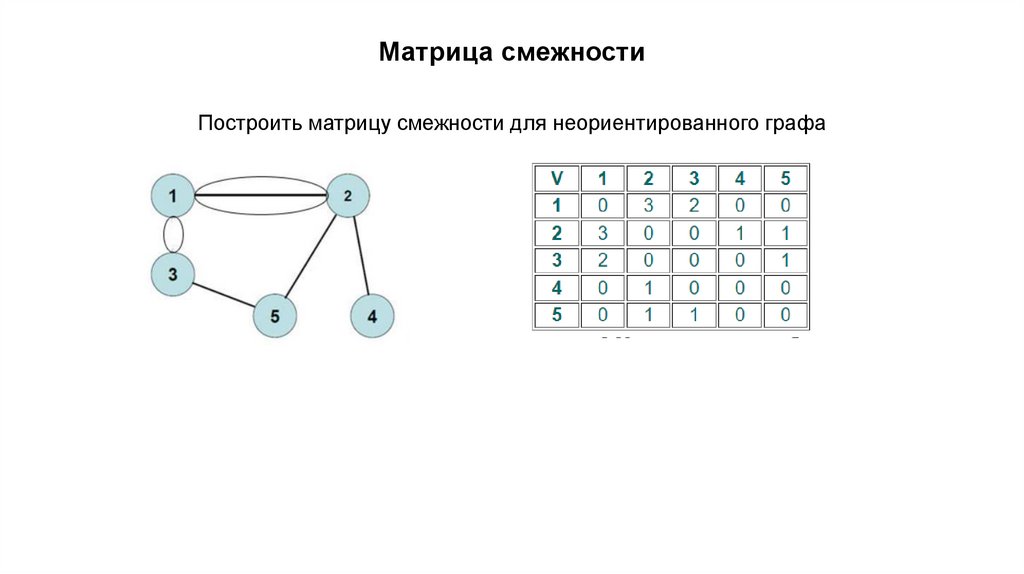
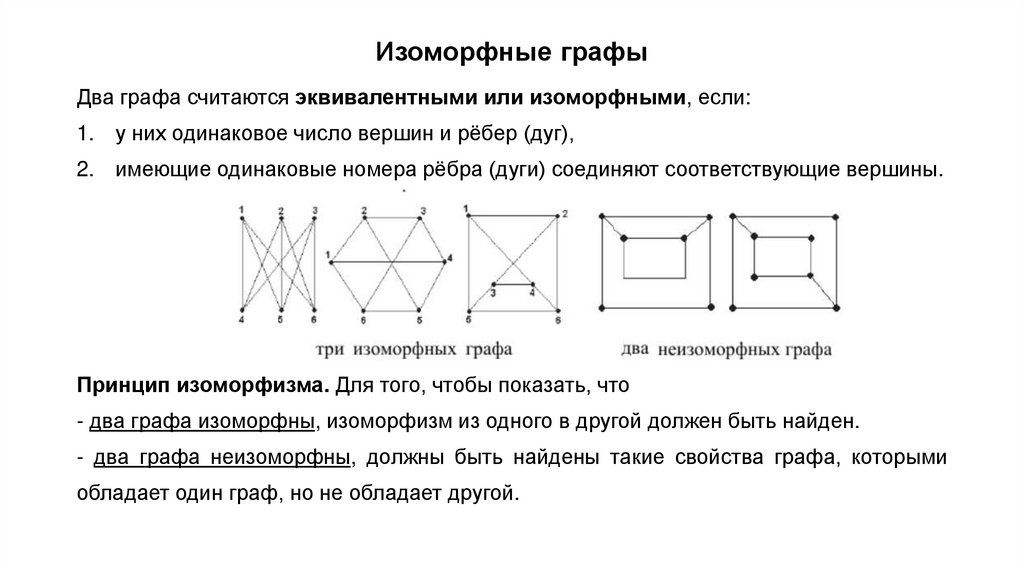
4. Изоморфные графы. Матрица смежности
5. Элементы графа
6. Число вершин нечётной степени. Лемма о рукопожатиях
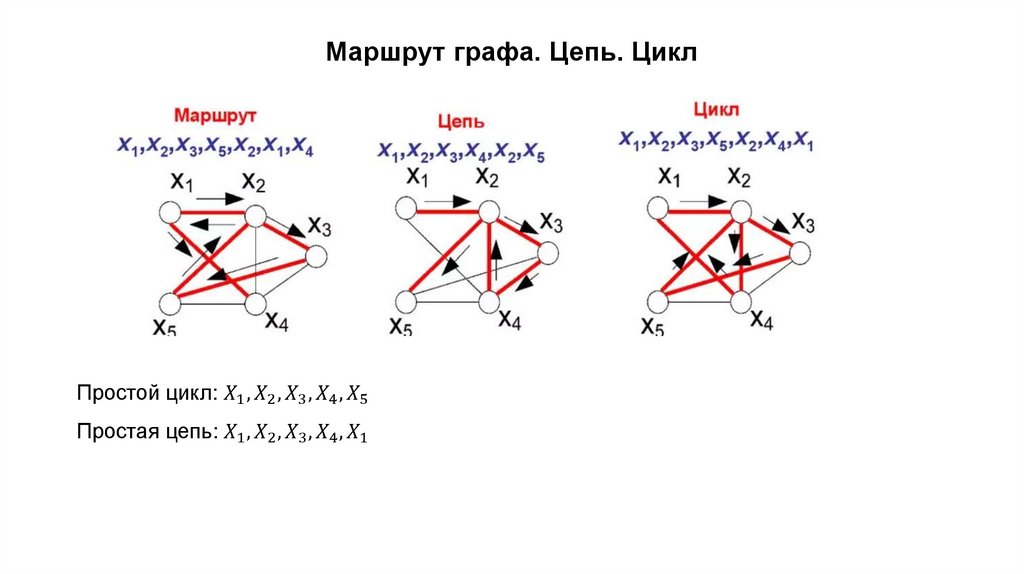
7. Маршрут графа. Цепь. Цикл
8. Путь, контур, петля
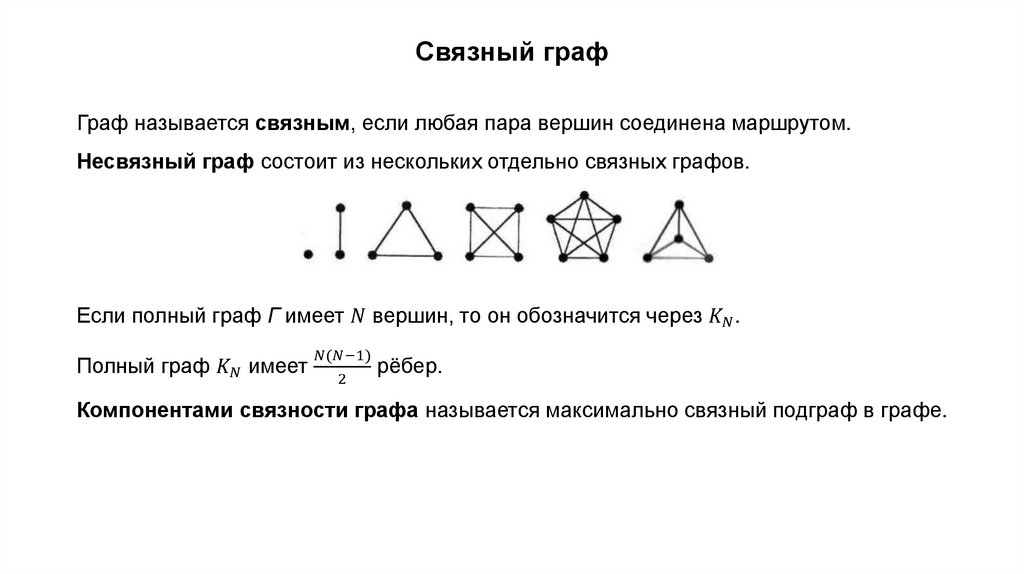
9. Связный, плоский, простой граф. Турнир
10. Плоские и планарные графы
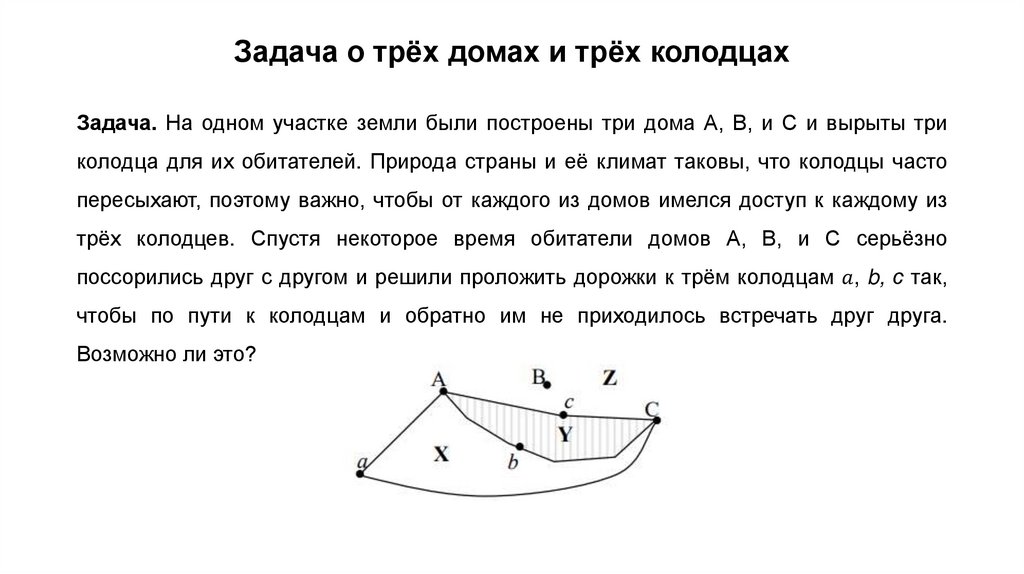
11. Задача о трех домах и трех колодцах
12. Графы Куратовского
13. Расширение и сжатие графа
14. Грань плоского графа
15. Бесконечная грань
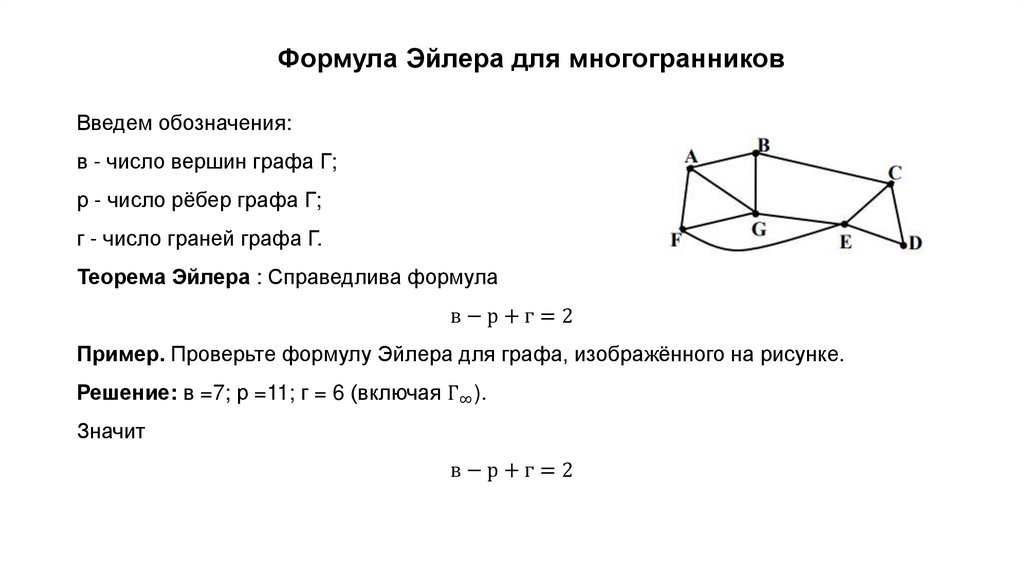
16. Формула Эйлера для многогранников

3.

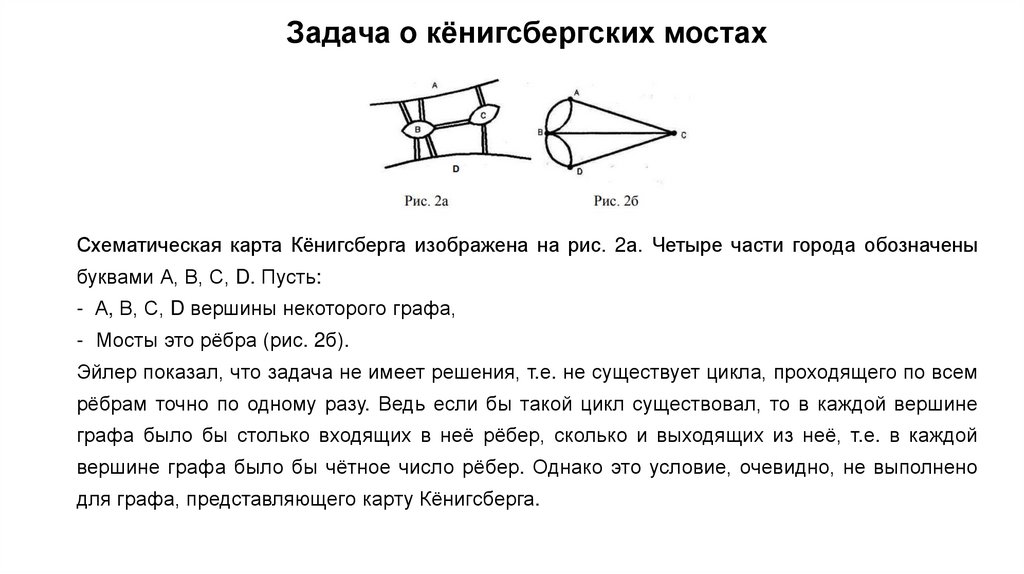
Введение
Датой рождения теории графов считают 1736 год.
В этот год была опубликована статья Леонарда Эйлера, посвящённая решению
головоломки «Задача о кёнигсбергских мостах». Долгое время методы, аналогичные
эйлеровым, использовались для исследования развлекательных задач.
В XIX веке Г. Кирхгоф и А. Кэли с помощью графов стали описывать электрические (Г.
Кирхгоф ) и химические (А. Кэли ) «цепи» и «деревья».
Существующее название за наукой закрепилось в 1936 году, после выхода монографии
венгерского математика Д. Кёнига.
Термин «граф» происходит от греческого слова «пишу». Он говорит о наглядной
графической интерпретации основных понятий этой теории и о тесной связи её с
геометрией, топологией, комбинаторикой и рядом других математических дисциплин и
интенсивно использует их методы.

4.

Введение
На языке теории графов формулируются и решаются следующие задачи:
1. Теории управления, в том числе задачи сетевого планирования и управления,
2. Анализа и проектирования организационных структур,
3. Анализа процессов функционирования динамических систем,
4. Анализа соединения в электрической цепи,
5. Схем перекрестков и дорог,
6. Множество предприятий с указанием двухсторонних связей между ними,
7. Групп людей с указанием их психологической совместимости и т. д.

5.

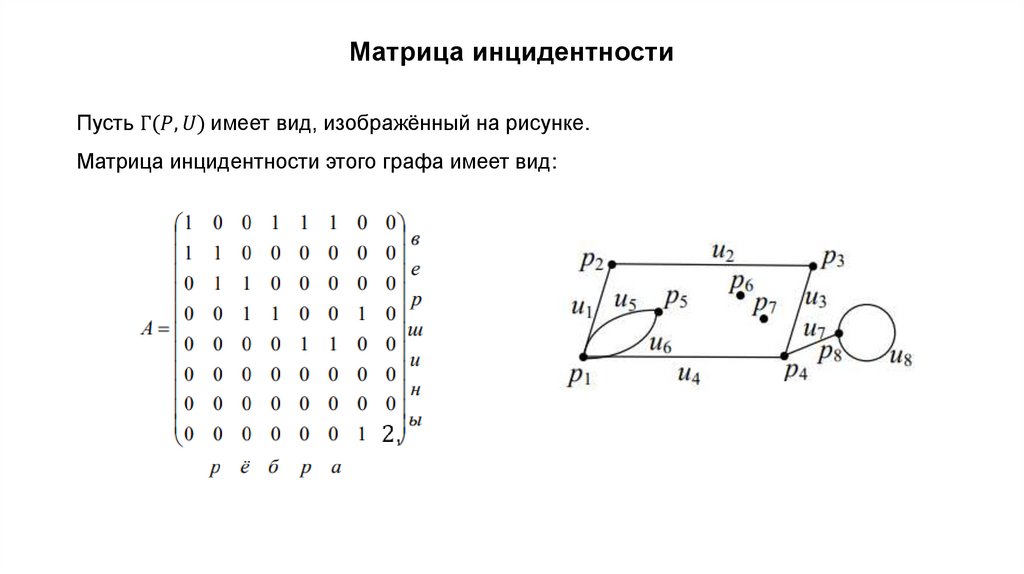
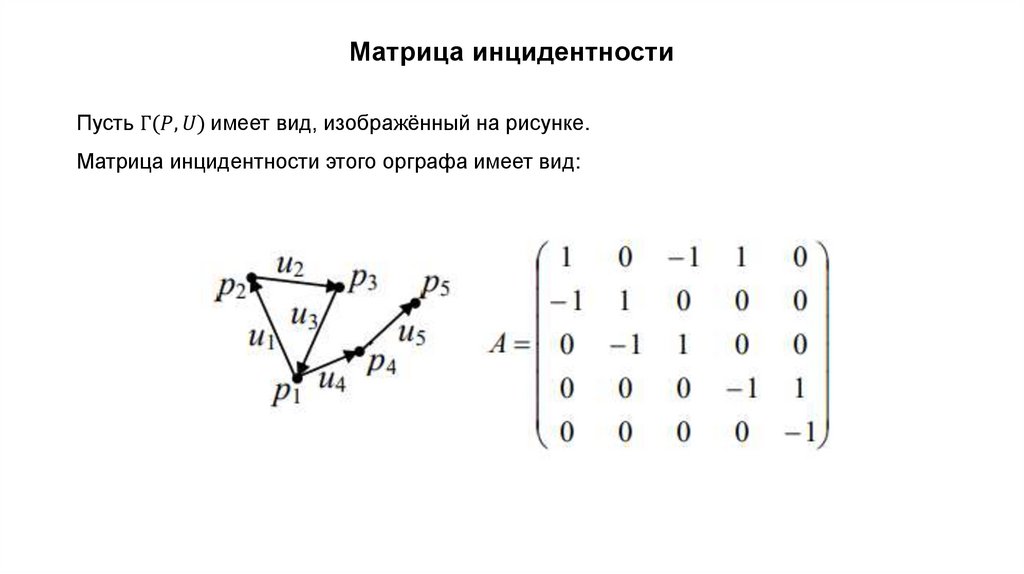
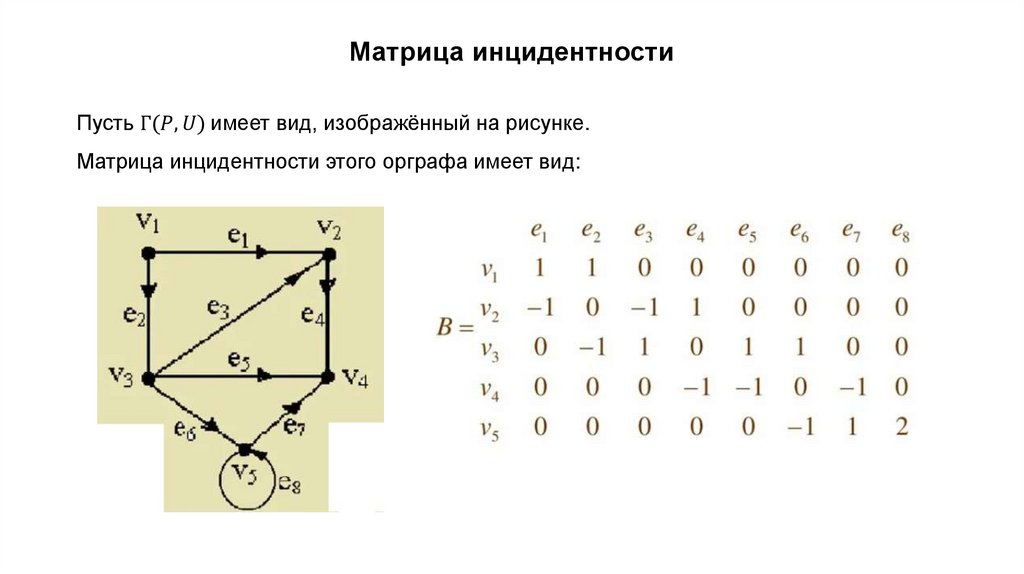
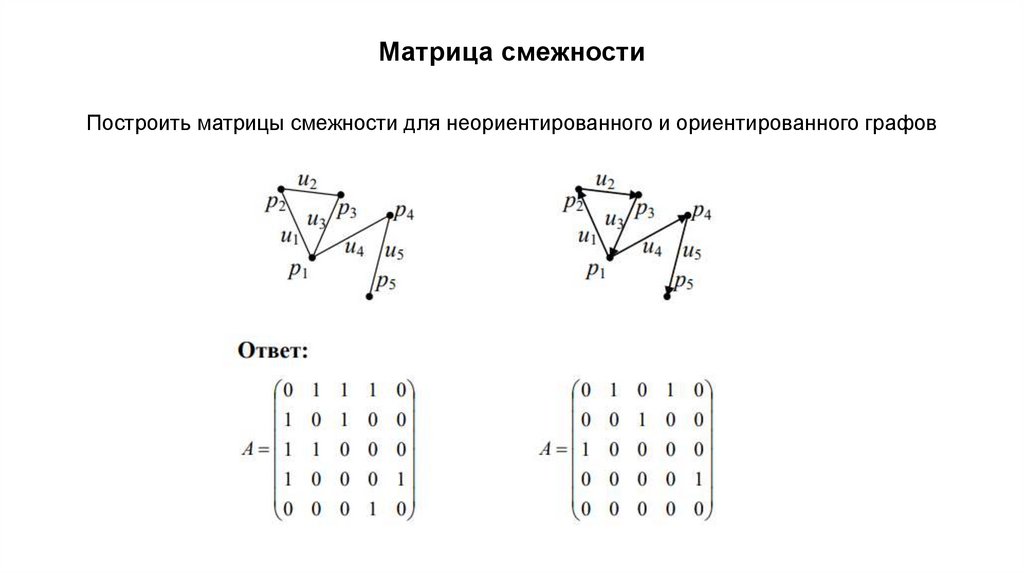
Основные понятия
Графом называется совокупность точек (объектов) и соединяющих их линий (связей).
Точки графа при этом называются его вершинами, а связывающие их линии –
рёбрами.
Пусть в графе имеется: