Прочность материалов

1.

Прочность материалов,
или почему все ломается?

2.

Конструкция - материальное образование
любого рода, предназначенное для того,
чтобы выдерживать нагрузки.

3. Живые конструкции

Биологические конструкции возникли несравненно раньше искусственных.
Изобретая жизнь, природа оказалась перед необходимостью создать для
нее какое-то вместилище. Соответствующие пленки или мембраны должны
были обладать хотя бы минимальной механической прочностью как для
того, чтобы удерживать живую материю, так и для того, чтобы
противостоять внешним воздействиям.

4.

Живые конструкции
Постепенно, по мере роста числа живых существ, обострялась
конкуренция, шансы выжить для слабых, неповоротливых и
малоподвижных существ падали. Оболочки становились прочнее,
совершенствовались способы передвижения. Появились большие
многоклеточные организмы, которые уже могли кусаться и
быстро плавать. Охотиться и быть преследуемым, есть и быть
съеденным - вот что определяло выживание.

5.

Живые конструкции
Примитивные существа наиболее раннего периода
были большей частью из мягких материалов не только
потому, что это позволяло им легче извиваться и
менять форму, но и потому, что мягкие ткани обычно
оказываются вязкими, тогда как твердые, подобные
костям, зачастую весьма хрупки.

6. Живые конструкции

Создается впечатление, что природа использует жесткие материалы
довольно неохотно, однако с ростом размеров и выходом животных
из воды на сушу эволюция, как правило, награждала их твердыми
скелетами, зубами, а иногда рогами и панцирем. Все же в отличие от
большинства современных механизмов животные никогда не
становились полностью твердыми. Обычно скелет составляет
лишь небольшую часть туловища и, как мы увидим ниже, мягкие
части туловища очень часто ограничивают приходящиеся на него
нагрузки, защищая скелет от неблагоприятных последствий
собственной хрупкости.

7.

Живые конструкции
В то время как у животных большую часть тела
составляют, как правило, гибкие, податливые
материалы, у растений это не всегда так.
Небольшие и наиболее примитивные растения
обычно бывают мягкими - ведь им не
приходится ни добывать себе пропитание
охотой, ни убегать от врага.
Зато для растения важно быть высоким, что до
некоторой степени уберегает от недругов и
позволяет получать больше света и влаги.
Деревьям особенно хорошо удается не только
тянуться вверх, но и противостоять порывам
ветра.
Превосходя другие живые конструкции по срокам
жизни
и
размерам,
деревья
порой
дотягиваются до 110 метров.

8. Технические конструкции

Поскольку
при
разрушении
инженерных конструкций
возможны человеческие
жертвы,
поведение
технических
конструкций
исследуется
с
предельной
тщательностью.

9. Технические конструкции

В
некоторых
областях
конструирования
люди
практики
веками
действовали
по
своему
собственному разумению.
Глядя на кафедральный
собор, спрашиваешь себя,
что впечатляет в большей
степени - мастерство тех,
кто его строил, или их вера в
успех. Эти сооружения не
только имеют гигантскую
высоту
и
размеры,
но
зачастую
им
удается
преодолеть
тяжесть
материала, из которого они
построены

10. Технические конструкции

Может показаться, что средневековые
каменщики знали, как строить церкви и
соборы, а потому это им так блестяще
удавалось.
Но если бы можно было спросить такого
Мастера, как все это делалось и почему
вообще сооружение не рухнуло, он, я
думаю, ответил бы нечто вроде: "На все
воля Божья".
Мы
любуемся
сохранившимися
постройками средневековых каменщиков,
но успех сопутствовал им отнюдь не
всегда.
Многим дерзким замыслам не суждено
было
осуществиться:
постройки
рушились
и
в
процессе
строительства, и вскоре после его
окончания.

11. Технические конструкции

Каменная кладка находится в более или менее
исключительном положении, и не случайно иногда
только опыт и традиционные пропорции
позволяют безопасно и целесообразно воздвигать
каменные сооружения любых размеров - от
небольших церквушек до громадных соборов.
Для иного рода конструкций это совершенно
неприемлемо и далеко не безопасно. Именно
этим определяется тот факт, что здания строят все
больших
размеров,
а,
например,
размер
кораблей, по сути дела, уже долгое время не
меняется.
Пока не существовало научного метода оценки
безопасности конструкций, вероятность беды
при
создании
новых
или
существенно
видоизмененных сооружений была весьма велика.

12. ПОЧЕМУ КОНСТРУКЦИИ ВЫДЕРЖИВАЮТ НАГРУЗКИ

Как получается, что любое неодушевленное твердое тело - из
стали, камня, дерева или пластмассы - вообще способно
оказывать сопротивление механической силе или хотя бы
выдерживать свой собственный вес. Это, в сущности, задача
о том, "почему мы не проваливаемся сквозь пол "
Роберт Гук (1635-1703)

13. ПОЧЕМУ КОНСТРУКЦИИ ВЫДЕРЖИВАЮТ НАГРУЗКИ

В тех случаях, когда материал или конструкция оказывает
сопротивление действию нагрузки, это возможно только за
счет их ответного действия на тело, создающее эту
нагрузку, с силой, равной по величине и противоположной
по направлению. Если ваши ноги давят на пол вниз, то пол
должен давить на ваши ноги вверх. Если кафедральный
собор давит вниз на свое основание, то основание должно
давить вверх на собор.
Это подразумевается в третьем законе Ньютона,
который, напомним, гласит, что действие и
противодействие
равны
по
величине
и
противоположны по направлению.

14. ПОЧЕМУ КОНСТРУКЦИИ ВЫДЕРЖИВАЮТ НАГРУЗКИ

Каждая сила должна быть уравновешена другой силой,
равной ей по величине и противоположной по
направлению, в каждой точке конструкции.
Это справедливо для любых конструкций независимо от того,
малы ли они и просты или велики и сложны. Если это
условие нарушено, то есть если где-то нарушено статическое
равновесие, то либо конструкция развалится, либо она должна
двигаться ускоренно

15.

Самолет, в котором деформация
лонжеронов крыла составляет 1,6%

16. Арка, представляющая собой конструкцию, работающую на сжатие в двух направлениях

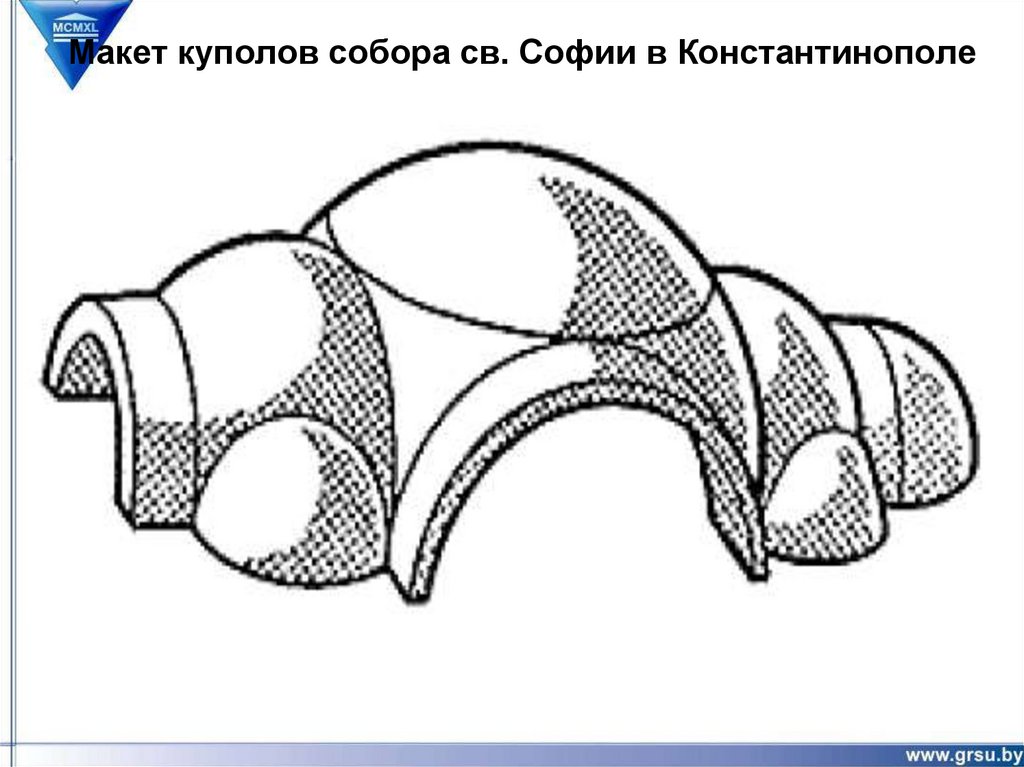
17. Макет куполов собора св. Софии в Константинополе

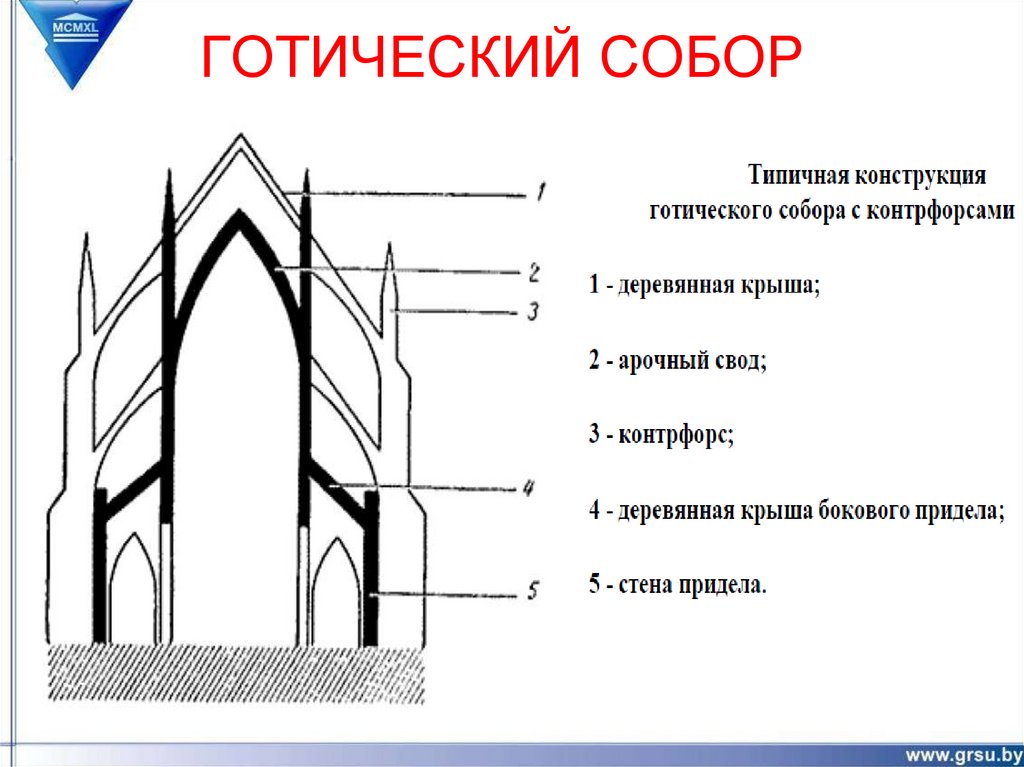
18. ГОТИЧЕСКИЙ СОБОР

19. ПОЧЕМУ КОНСТРУКЦИИ ВЫДЕРЖИВАЮТ НАГРУЗКИ

Предположим, мы подвешиваем с помощью веревки
кирпич к опоре (ветка дерева). Вес кирпича
обусловлен воздействием гравитационного поля
Земли на его массу, и сила веса всегда направлена
вниз. Кирпич не упадет, если его удерживает в
воздухе постоянно действующая сила, равная по
величине его весу и направленная вверх - в
данном случае натяжение веревки. Если веревка
слишком слаба и не может создать направленную
вверх силу, равную весу кирпича, то она неминуемо
оборвется и кирпич упадет на Землю.
Рис. 1. Направленная вниз сила веса
кирпича должна быть уравновешена
равной по величине и
противоположной по направлению
силой натяжения веревки

20. ПОЧЕМУ КОНСТРУКЦИИ ВЫДЕРЖИВАЮТ НАГРУЗКИ

Если кирпич подвешен к ветке дерева, то груз удерживается
за счет растяжения веревки, другими словами, за счет
натяжения. Во многих конструкциях, таких, как здания,
нагрузка выдерживается за счет сжатия, давления.
Уже в 1676 г. Гук ясно понимал не только то, что
сопротивление твердых тел силам веса или другим
механическим нагрузкам создается посредством сил
противодействия, но и то, что, во-первых, под механическим
воздействием всякое твердое тело меняет свою форму,
растягиваясь или сжимаясь, а во-вторых, именно это
изменение формы и позволяет твердому телу создавать
силу противодействия.

21. ПОЧЕМУ КОНСТРУКЦИИ ВЫДЕРЖИВАЮТ НАГРУЗКИ

Все материалы и конструкции,
хотя и в очень различной степени,
под действием нагрузки
испытывают смещения (рис. 2).
Рис.2. Под действием веса
обезьяны материал ветки
растянут у ее верхней
поверхности и сжат у нижней.

22.

Теория упругости - это наука о соотношениях между
силами и смещениями в материалах и конструкциях.
Величины смещений, которые встречаются на
практике,
могут
изменяться
в
огромных
пределах. Так, в растении, куске резины
смещения, как правило, велики и их легко
наблюдать, а в случаях, когда мы прикладываем
обычные нагрузки к таким твердым веществам, как
металл, бетон или кость, смещения на самом
деле иногда оказываются очень малыми.
Если
вы
взберетесь
на
колокольню
кафедрального собора, в результате добавления
вашего веса он станет ниже, пусть на весьма
малую величину. Каменная кладка на самом деле
оказывается более гибкой, чем можно было бы
предполагать. Вы можете убедиться в этом,
посмотрев
на
4
главные
колонны,
поддерживающие колокольню собора в Солсбери:
все
они
заметно
изогнуты
(рис.
3).
Рис. 3 Каменная
кладка является намного более
гибкой, чем обычно думают.

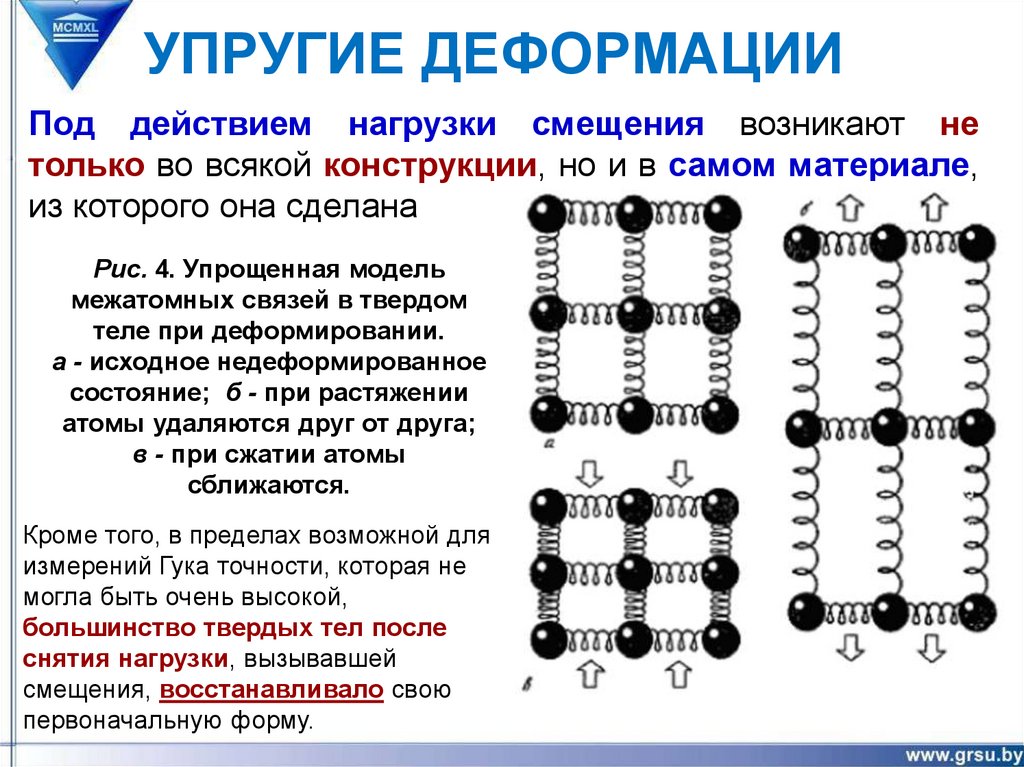
23. УПРУГИЕ ДЕФОРМАЦИИ

Под действием нагрузки смещения возникают не
только во всякой конструкции, но и в самом материале,
из которого она сделана
Puc. 4. Упрощенная модель
межатомных связей в твердом
теле при деформировании.
а - исходное недеформированное
состояние; б - при растяжении
атомы удаляются друг от друга;
в - при сжатии атомы
сближаются.
Кроме того, в пределах возможной для
измерений Гука точности, которая не
могла быть очень высокой,
большинство твердых тел после
снятия нагрузки, вызывавшей
смещения, восстанавливало свою
первоначальную форму.

24.

ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ
В то же время форма некоторых твердых и "почти твердых" тел,
таких, как замазка, пластилин, полностью не восстанавливается,
они остаются деформированными и после снятия нагрузки. Такое
поведение называется пластическим.

25.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
Напряжение
К представлению о напряжении был очень близок еще Галилей. В "Двух
новых науках" - книге, написанной им в старости, - он указывает, что
растягиваемый стержень имеет прочность, которая при постоянстве
остальных условий пропорциональна площади его поперечного
сечения. Иными словами, если стержень сечением 2 см разрывается при
нагрузке 1000 кгс, то стержень сечением 4 см разрывается при нагрузке 2000
кгс. Кажется почти невероятным, что потребовалось почти два столетия,
чтобы разделить разрушающую нагрузку на площадь поверхности в месте
разрыва, дабы получить величину, называемую сегодня разрушающим
напряжением (в упомянутом выше случае 500 кгс/см2) и относящуюся ко
всем стержням из того же материала.
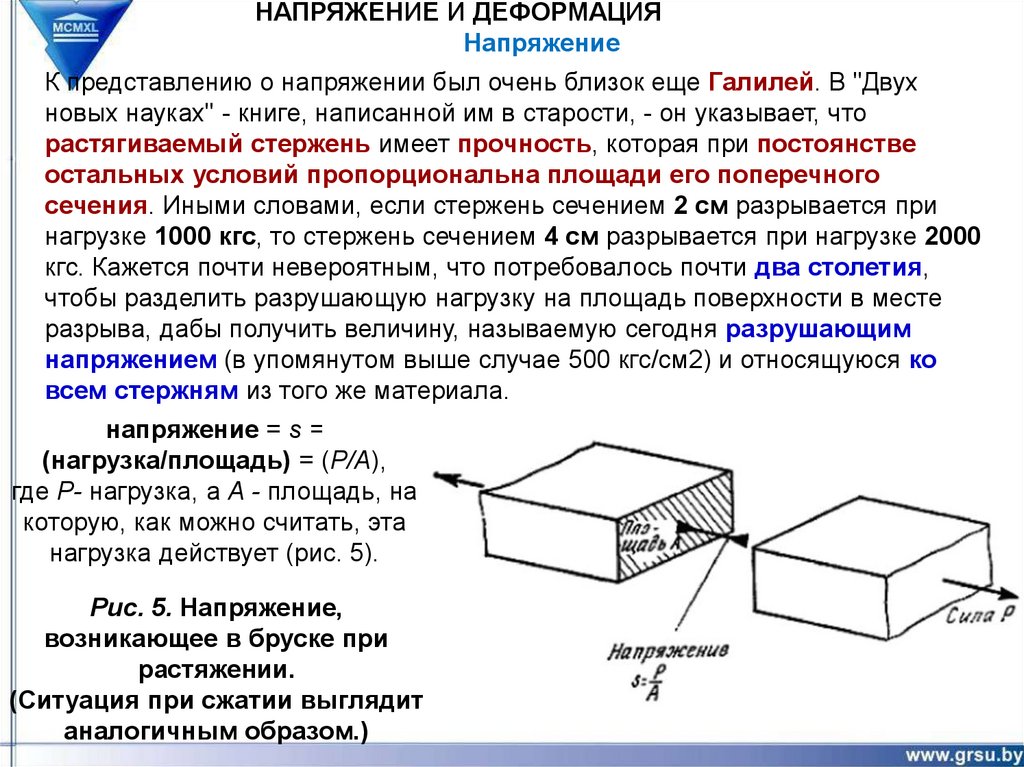
напряжение = s =
(нагрузка/площадь) = (Р/А),
где Р- нагрузка, а А - площадь, на
которую, как можно считать, эта
нагрузка действует (рис. 5).
Рис. 5. Напряжение,
возникающее в бруске при
растяжении.
(Ситуация при сжатии выглядит
аналогичным образом.)

26.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
Деформация
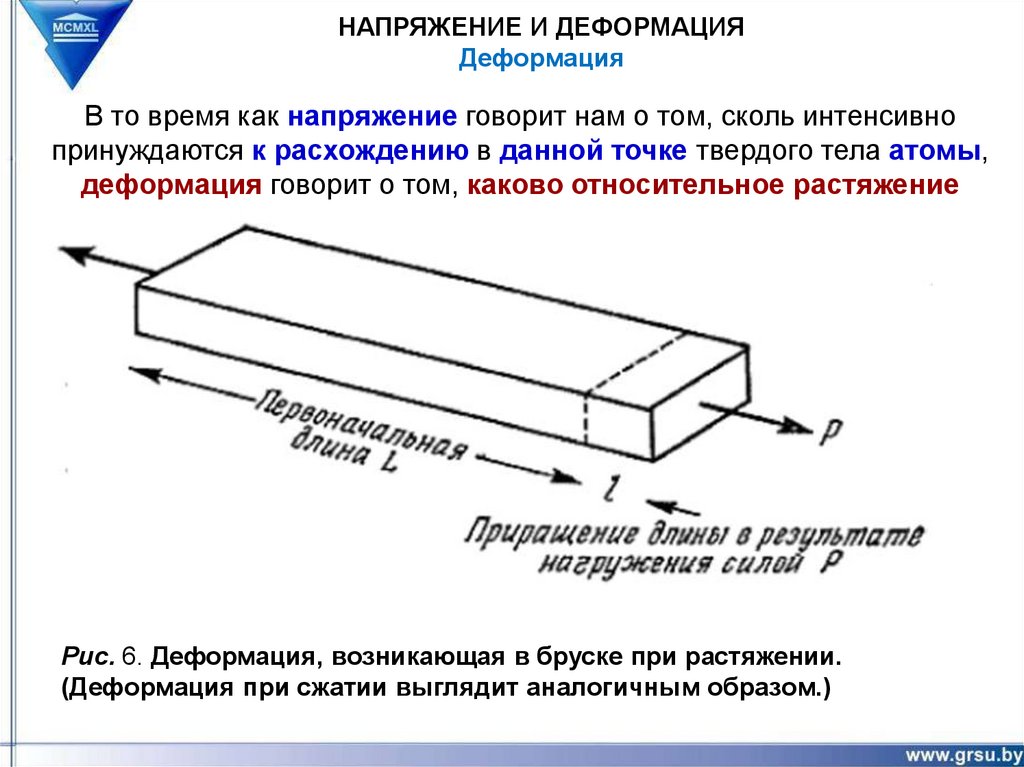
В то время как напряжение говорит нам о том, сколь интенсивно
принуждаются к расхождению в данной точке твердого тела атомы,
деформация говорит о том, каково относительное растяжение
межатомных связей
Рис. 6. Деформация, возникающая в бруске при растяжении.
(Деформация при сжатии выглядит аналогичным образом.)

27.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
Деформация
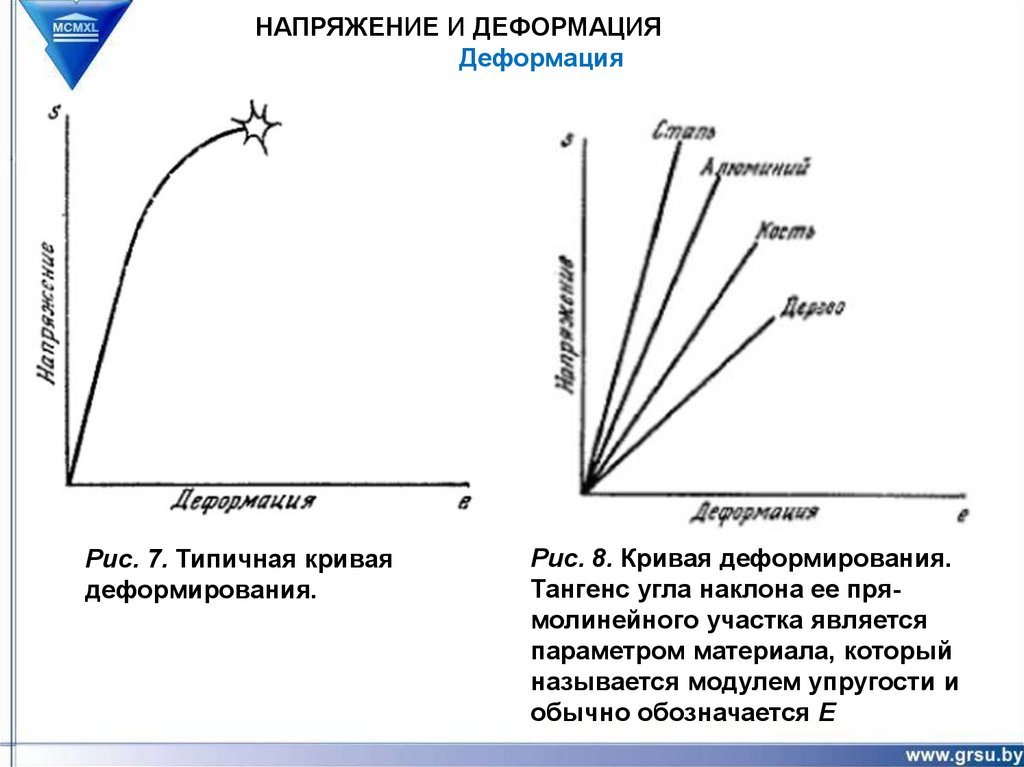
Рис. 7. Типичная кривая
деформирования.
Рис. 8. Кривая деформирования.
Тангенс угла наклона ее прямолинейного участка является
параметром материала, который
называется модулем упругости и
обычно обозначается Е

28.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ Прочность
Не следует путать прочность конструкции и прочность материала.
Прочность конструкции определяется нагрузкой (в Н или в кг),
которая приводит к разрушению конструкции. Эта величина
известна как разрушающая нагрузка, и она обычно используется
только применительно к некоторой конкретной конструкции.
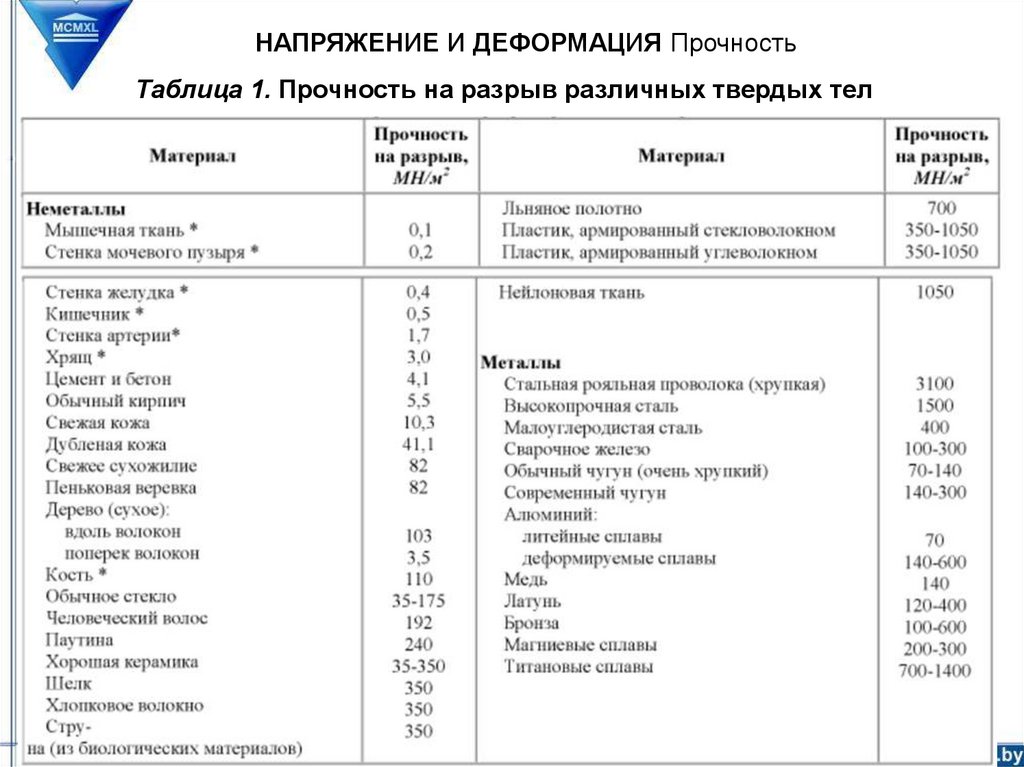
Прочность материала характеризуется напряжением (в МН/м2 или в
кгс/см2), разрушающим сам материал. Обычно величина прочности
более или менее постоянна для всех образцов данного вещества.
Мы в основном будем рассматривать прочность материалов при
растяжении, которую называют прочностью на разрыв.

29.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ Прочность
Таблица 1. Прочность на разрыв различных твердых тел

30.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ Прочность
Коэффициент запаса и коэффициент незнания
Примерно с 1850 г. инженеры вынуждены были начать
рассчитывать на прочность ответственные конструкции,
например крупные мосты. Пользуясь разработанными к
тому времени методами, они вычисляли наибольшие
возможные напряжения в конструкции и следили за тем,
чтобы они не превышали некоторой узаконенной
официальными нормами прочности материала на разрыв.
Для полной безопасности они делали наибольшее
вычисленное
действующее
напряжение
много
меньшим - в 3-4 или даже в 7-8 раз, - чем прочность
материала, найденная путем разрушения простых,
однородных его образцов, очень аккуратно нагружаемых в
лабораторной установке. Эту процедуру они называли
введением коэффициента запаса. Любая попытка
уменьшения веса и стоимости за счет снижения
коэффициента запаса грозила обернуться бедой.

31.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ Прочность
Все более частыми становились катастрофы на море. Требования к
повышению скорости и снижению веса судов породили трудности
и для кораблестроителей: у кораблей возникла тенденция
разламываться в открытом море надвое, хотя наибольшие
расчетные напряжения казались вполне умеренными и безопасными.
Так, в 1901 г. внезапно разломился пополам и затонул в Северном
море при нормальной погоде совершенно новый корабль "Кобра",
в то время один из самых быстроходных кораблей мира.

32.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ Прочность
Корабль "Скенектеди". Трещина началась у острого угла люка на палубе
и"побежала" до самого киля

33.

Концентрация напряжений, или как "запустить" трещину
Отверстия, трещины, острые углы и другие особенности поверхности,
на которые раньше не обращали внимания, повышают локальные
напряжения; такие области повышенных напряжений могут быть очень
малыми, но последствия - весьма драматическими. В окрестности
отверстия или надреза напряжения могут значительно превышать
разрушающие напряжения для данного материала даже в тех случаях,
когда общий средний уровень напряжении невысок и конструкция
кажется вполне безопасной.
Этот факт был известен кондитерам, которые делали желобки в
плитках шоколада, и тем, кто имел дело с почтовыми марками, в
которых пробивались ряды дырочек. А вот инженеры до того времени
почти не проявляли интереса к вопросам образования трещин и не
считали, что они имеют отношение к инженерному делу.

34.

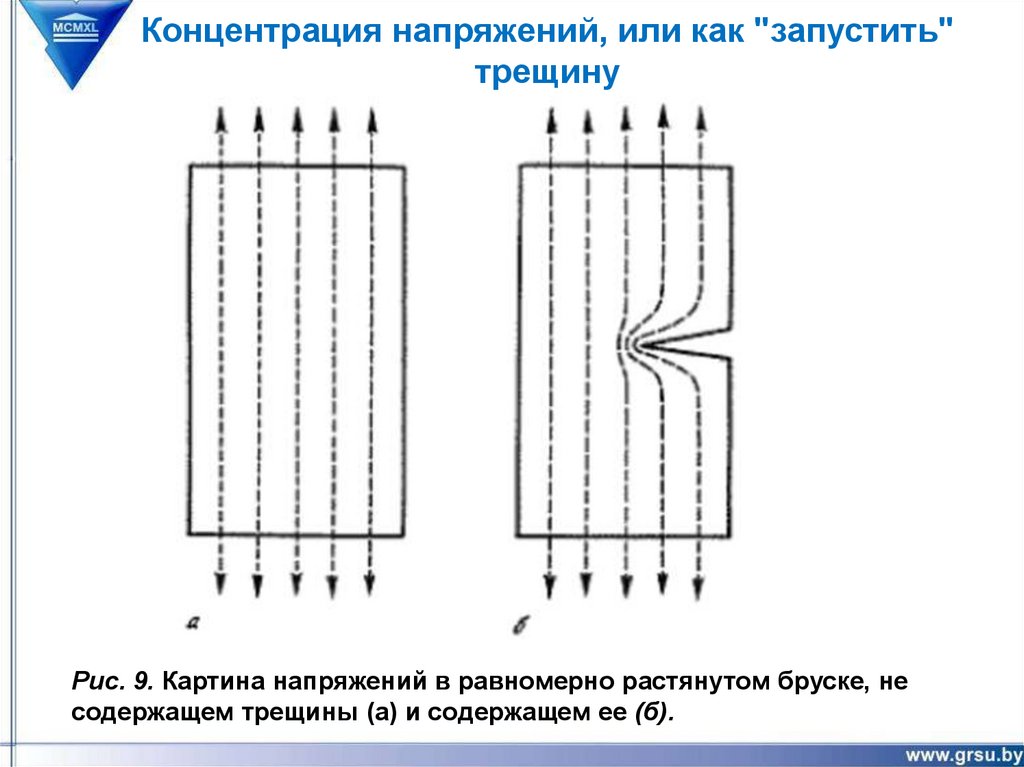
Концентрация напряжений, или как "запустить"
трещину
Рис. 9. Картина напряжений в равномерно растянутом бруске, не
содержащем трещины (а) и содержащем ее (б).

35.

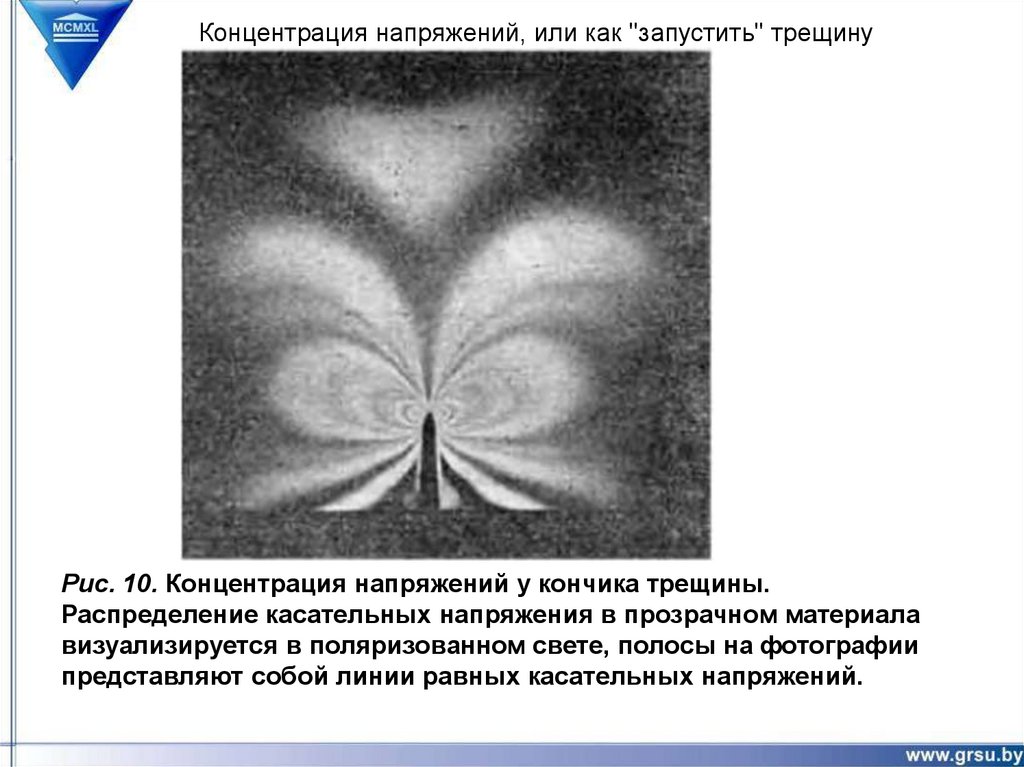
Концентрация напряжений, или как "запустить" трещину
Рис. 10. Концентрация напряжений у кончика трещины.
Распределение касательных напряжения в прозрачном материала
визуализируется в поляризованном свете, полосы на фотографии
представляют собой линии равных касательных напряжений.

36.

Чтобы ослабить материал, даже не нужно искусственно создавать
надрезы - концентраторы напряжений. Твердые тела еще до создания из
них конструкций, как правило, содержат множество всевозможных пор,
щелей и трещин. По этой причине нельзя подвергать хрупкие твердые
тела заметным растягивающим напряжениям. Их, конечно, широко
используют при возведении стен, строительстве дорог и т. и., где они
работают на сжатие. В тех случаях, когда нельзя избежать
некоторого растяжения, как, например, в оконных стеклах,
необходимо позаботиться о том, чтобы эти напряжения были
достаточно малыми, и вводить большой коэффициент запаса
прочности.

37.

Следует отметить, что не только отверстия, трещины и другие
пустоты могут быть причиной понижения прочности материала.
Вызвать концентрацию напряжений может, наоборот, и добавка
материала, если это приводит к резкому локальному увеличению
жесткости. Так, если поставить заплату из нового материала на старую
одежду или толстый лист брони на тонкий борт военного корабля, из
этого не получится ничего хорошего.
Причина здесь в следующем. Траектории напряжений могут столь же
сильно притягиваться к более жесткой области (заплате), как и
отталкиваться от области с более низкой жесткостью (отверстия).
Любой элемент конструкции, отличающийся от окружающих его
элементов своими упругими свойствами, вызывает концентрацию
напряжений и может быть опасным.

38.

Упругая энергия как причина разрушения
Чтобы разорвать материал, в нем должна возникнуть трещина. Однако,
чтобы такая трещина продвинулась на своем пути, необходимо
затратить энергию, которую надо где-то взять. Можно без труда
сломать лук, "стреляя" из него без стрелы. При этом запасенная в луке
упругая энергия не может благополучно высвободиться и перейти в
кинетическую энергию стрелы, а потому часть ее идет на образование
трещин в материале самого лука.
.
Другими словами, упругая
энергия лука его же и
ломает.
Все
упругие
вещества, находящиеся под
действием
нагрузки,
содержат
большее
или
меньшее
количество
упругой энергии, и эта
энергия
потенциально
всегда может пойти на
процесс разрушения их
самих

39.

Упругая энергия как причина разрушения
Ответ на вопрос, поломается ли на самом деле конструкция в любом
заданном месте, зависит от того, может ли упругая энергия перейти в
энергию разрушения так, чтобы образовать трещину.
Независимо от того, подвергается ли конструкция удару
или действию статической нагрузки, разрушение путем
разрыва зависит главным образом от следующего:
1) от цены в единицах энергии, которую нужно
заплатить, чтобы протолкнуть трещину;
2) от количества упругой энергии, которым
располагает конструкция, готовая заплатить указанную
цену;
3) от размеров и формы наиболее опасных
отверстий, трещин или дефектов конструкции.
Тот факт, что величины энергии, необходимые для того,
чтобы разрушить материал в любом данном
поперечном сечении, для различных твердых тел весьма
различны, легко подтвердить, ударив молотком сначала
по стеклянной, а потом по консервной банке.

40.

Энергия, или работа, разрушения
Когда твердое тело разрушается при растяжении, должна возникнуть
хотя бы одна трещина, распространение которой разделяет кусок
материала на части. Это означает, что должны образоваться по крайней
мере две новые поверхности, не существовавшие ранее, до
разрушения тела. Чтобы таким путем произвести в материале разрыв
и образовать эти новые поверхности, необходимо разорвать все
химические связи, до того сцеплявшие между собой поверхности.
Количество энергии, требуемое для
разрыва почти всех типов химических
связей, хорошо известно (по крайней
мере химикам), и оказывается, что для
большинства твердых тел, с которыми
мы имеем дело в технике, общие
количества энергии, требуемые для
разрыва всех связей по любой
единичной
плоскости
в
любом
поперечном сечении, весьма близки
между собой и не сильно отличаются от
величины 1 Дж/м2

41.

Хрупкие материалы
по возможности не используются там, где они могут подвергнуться
действию растяжений. Эти материалы являются хрупкими не
потому, что имеют низкую прочность на разрыв,- это означало бы,
что для их разрушения требуется небольшая сила, - а потому, что
для их разрушения требуется только небольшая энергия.
Технические и биологические материалы, которые используются
в условиях растяжения и в этом смысле являются относительно
безопасными, для образования новой поверхности при
разрушении требуют значительно большей энергии.
Другими
словами,
работа
разрушения для них значительно
больше, чем в случае хрупких
твердых тел. Для практически
вязкого
трещиностойкого
материала величина работы
разрушения обычно лежит в
пределах 103-106 Дж/м2.

42.

Поэтому энергия, требуемая для разрушения сварочного железа или
мягкой стали, может быть в 1000 000 раз больше энергии, требуемой
для разрушения в таком же поперечном сечении стекла или керамики,
хотя величины статической прочности на разрыв этих материалов не
сильно различаются. Поэтому таблица значений прочности на разрыв,
подобная табл. 1, в случае если ее используют для выбора какого-то
конкретного материала, может дезинформировать конструктора. По этой
же причине классическая теория упругости, основанная главным образом
на силах и напряжениях, которая старательно разрабатывалась в течение
столетий, - сама по себе не может правильно предсказывать
разрушение реальных материалов и конструкций.

43.

Таблица 2. Приближенные величины работы разрушения и прочности
при растяжении некоторых распространенных материалов

44.

Спасибо за внимание!