Similar presentations:
Отображения и соответствия. Счетные множества. Бинарные отношения
1.
Отображения и соответствия. Счетныемножества. Бинарные отношения
Основные виды соответствий и
отображений
Образ и прообраз множества
Композиция соответствий
Счетные множества
Континуальные множества
Кардинальные числа
Бинарные отношения
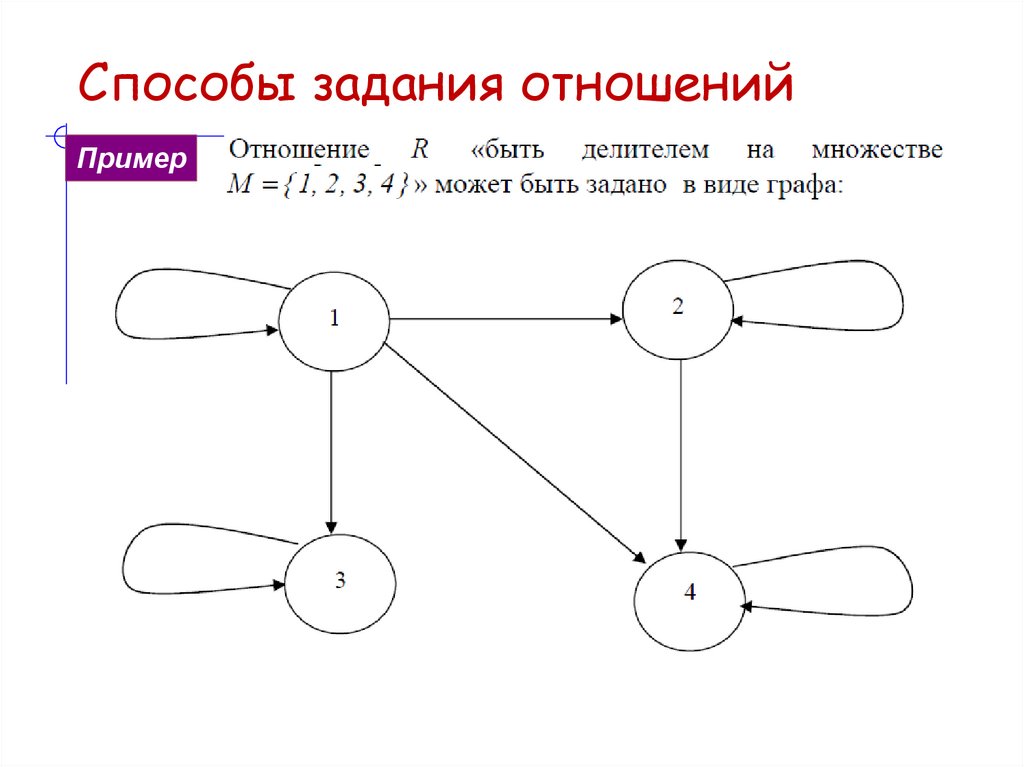
Способы задания отношений
Типы бинарных отношений
2.
Основные виды соответствий и отображений3.
Основные виды соответствий и отображенийПример инъективного
отображения
4.
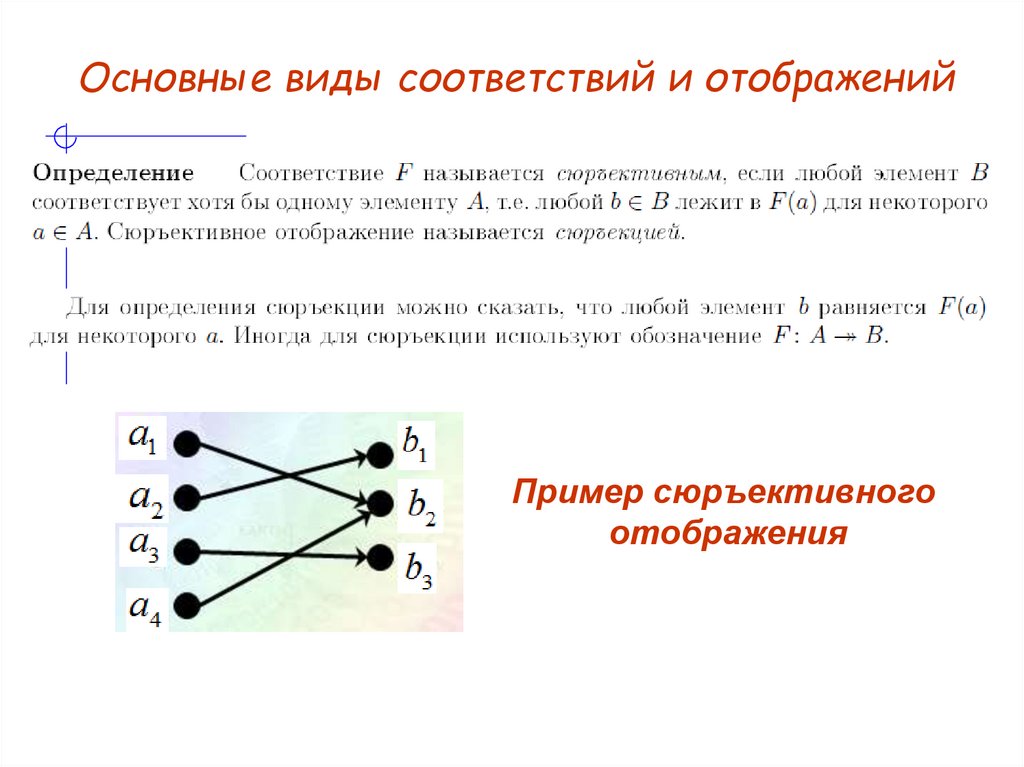
Основные виды соответствий и отображенийПример сюръективного
отображения
5.
Основные виды соответствий и отображенийПример биективного
отображения
6.
Основные виды соответствий и отображенийПример
7.
Образ и прообраз множествазначений
8.
Композиция соответствий9.
Композиция соответствий10.
Счетные множества11.
Счетные множестваПример
12.
Счетные множестваТеорема 1
Теорема 2
Теорема 3 (теорема Кантора)
13.
Континуальные множестваПример
14.
Кардинальные числа15. Бинарные отношения
В математике изучают не только связи между элементами двухмножеств, т. е. соответствия, но и связи между элементами одного
множества. Называют их отношениями.
Отношения многообразны. Между понятиями — это отношения
рода и вида, части и целого; между предложениями — отношения
следования и равносильности; между числами — «больше»,
«меньше», «равно», «больше на ...», «меньше на ...», «следует» и
др.
Определение
16. Бинарные отношения
Примерыа) Бинарными отношениями на множестве целых чисел Z являются:
б) Пусть М – множество целых, рациональных или вещественных чисел.
Бинарными отношениями на множестве целых, рациональных или
вещественных чисел М являются отношения
17. Бинарные отношения
в)Пусть М – множество сотрудников
отношениями на М являются отношения:
«быть начальником»,
«не быть начальником».
фирмы.
Бинарными
Пример
Пусть на множестве M = {2, 4, 6, 8} задано отношение «меньше».
Это означает, что для любых двух чисел из множества M можно
сказать, какое из них меньше:
2 < 4, 2 < 6, 2 < 8, 4 < 6, 4 < 8, 6 < 8.
Полученные неравенства можно записать иначе, в виде
упорядоченных пар: (2, 4), (2, 6), (2, 8), (4, 6), (4, 8), (6, 8).
























 mathematics
mathematics








