Расчёт разветвлённых электрических цепей. Правила Кирхгофа. Соединение источников тока. Конденсатор в цепи постоянного тока

1.

Расчёт разветвлённых
электрических цепей. Правила
Кирхгофа. Соединение
источников тока. Конденсатор
в цепи постоянного тока.

2.

Разветвленная электрическая цепь — это
электрическая цепь, состоящая из нескольких
замкнутых контуров, которые имеют общие участки
(в каждом контуре может быть несколько
источников).

3.

Составные части сложной разветвленной
электрической цепи:
Ветвь — участок цепи с последовательным
соединением элементов, через который протекает
один ток.
Узел — точка, где соединяются две и более ветви
цепи. На схемах узловое соединение обозначают в
виде точки.
Контур — несколько ветвей цепи, соединенных
таким образом, что образуют замкнутую фигуру.

4.

Основными методами расчета сложных
разветвленных электрических цепей
являются:
Метод эквивалентных преобразований
Расчет по уравнениям Кирхгофа
Метод контурных токов
Метод узловых напряжений (потенциалов)
Метод эквивалентного генератора

5.

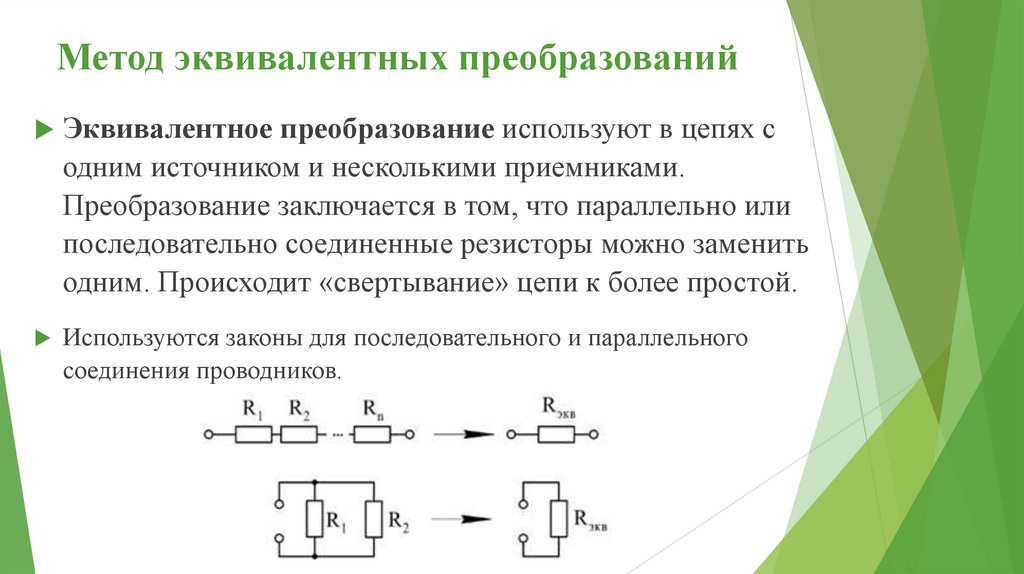
Метод эквивалентных преобразований
Эквивалентное преобразование используют в цепях с
одним источником и несколькими приемниками.
Преобразование заключается в том, что параллельно или
последовательно соединенные резисторы можно заменить
одним. Происходит «свертывание» цепи к более простой.
Используются законы для последовательного и параллельного
соединения проводников.

6.

Расчет по уравнениям Кирхгофа
Законы Кирхгофа являются основой для расчета
сложных разветвленных электрических цепей.
Первый закон Кирхгофа: алгебраическая сумма токов
в любом узле электрической цепи равна нулю.
Второй закон Кирхгофа: алгебраическая сумма
напряжений в замкнутом контуре равна нулю.

7.

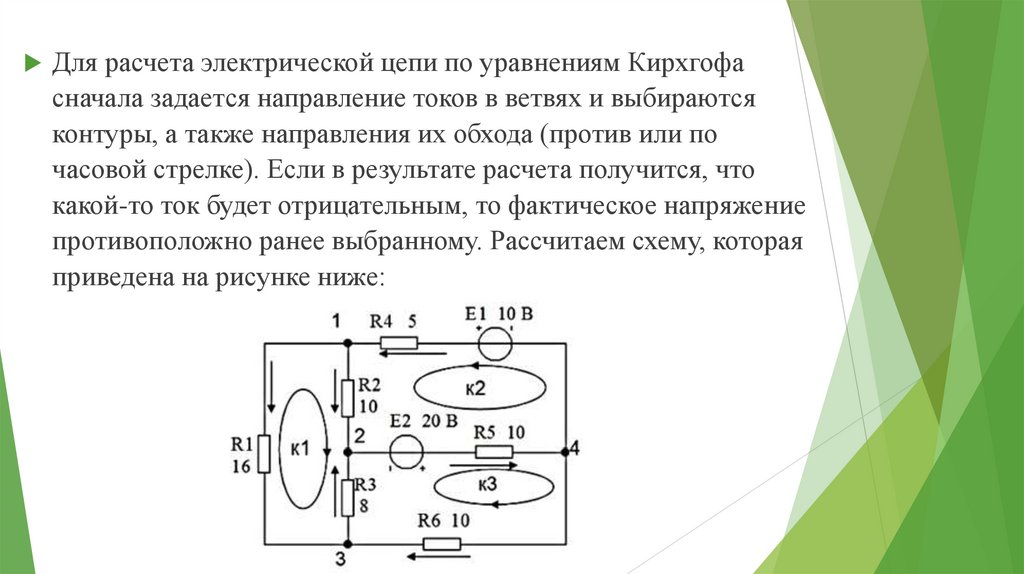
Для расчета электрической цепи по уравнениям Кирхгофа
сначала задается направление токов в ветвях и выбираются
контуры, а также направления их обхода (против или по
часовой стрелке). Если в результате расчета получится, что
какой-то ток будет отрицательным, то фактическое напряжение
противоположно ранее выбранному. Рассчитаем схему, которая
приведена на рисунке ниже:

8.

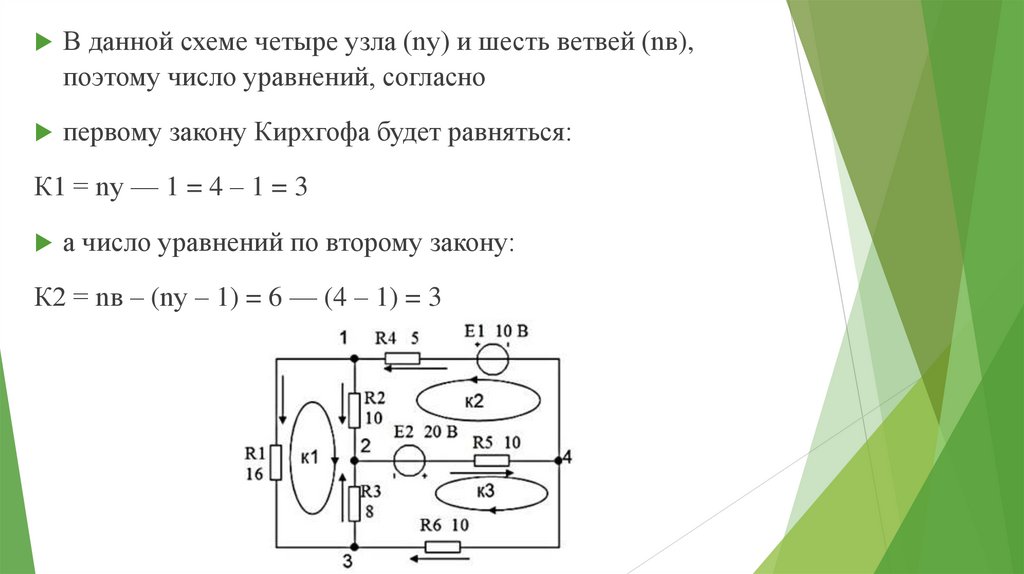
В данной схеме четыре узла (nу) и шесть ветвей (nв),
поэтому число уравнений, согласно
первому закону Кирхгофа будет равняться:
К1 = nу — 1 = 4 – 1 = 3
а число уравнений по второму закону:
К2 = nв – (nу – 1) = 6 — (4 – 1) = 3

9.

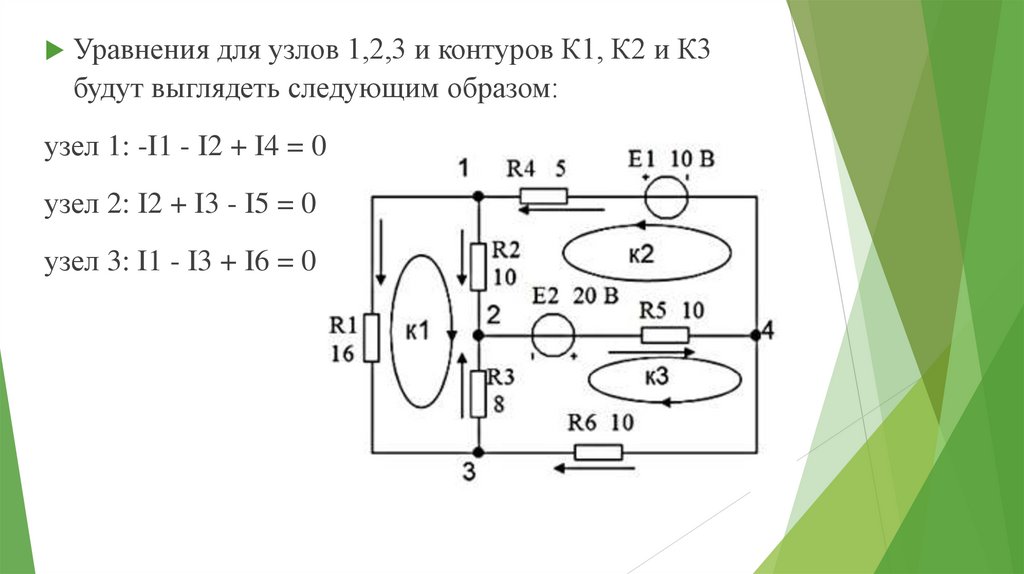
Уравнения для узлов 1,2,3 и контуров К1, К2 и К3
будут выглядеть следующим образом:
узел 1: -I1 - I2 + I4 = 0
узел 2: I2 + I3 - I5 = 0
узел 3: I1 - I3 + I6 = 0

10.

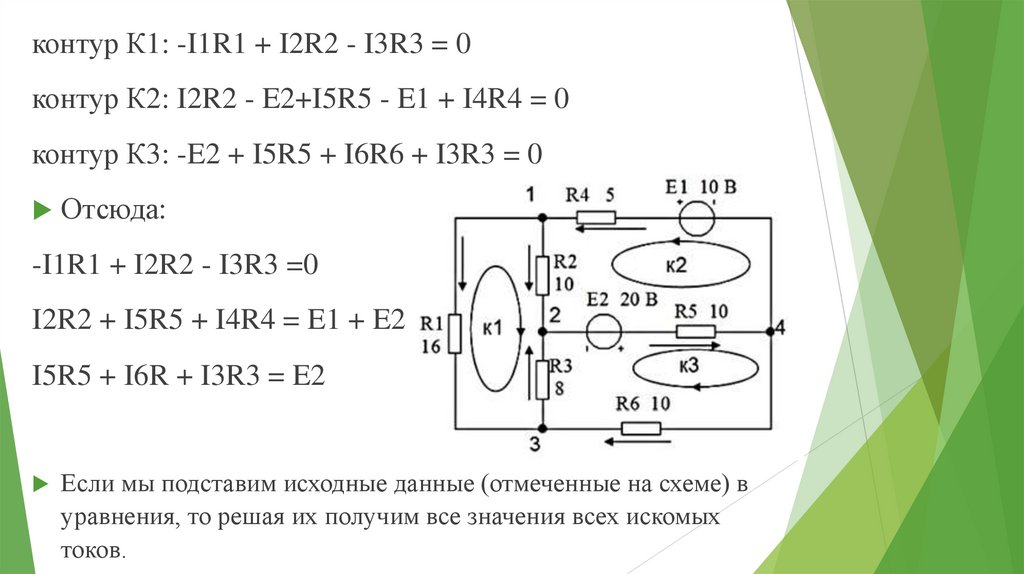
контур К1: -I1R1 + I2R2 - I3R3 = 0
контур К2: I2R2 - E2+I5R5 - E1 + I4R4 = 0
контур К3: -E2 + I5R5 + I6R6 + I3R3 = 0
Отсюда:
-I1R1 + I2R2 - I3R3 =0
I2R2 + I5R5 + I4R4 = E1 + E2
I5R5 + I6R + I3R3 = E2
Если мы подставим исходные данные (отмеченные на схеме) в
уравнения, то решая их получим все значения всех искомых
токов.

11.

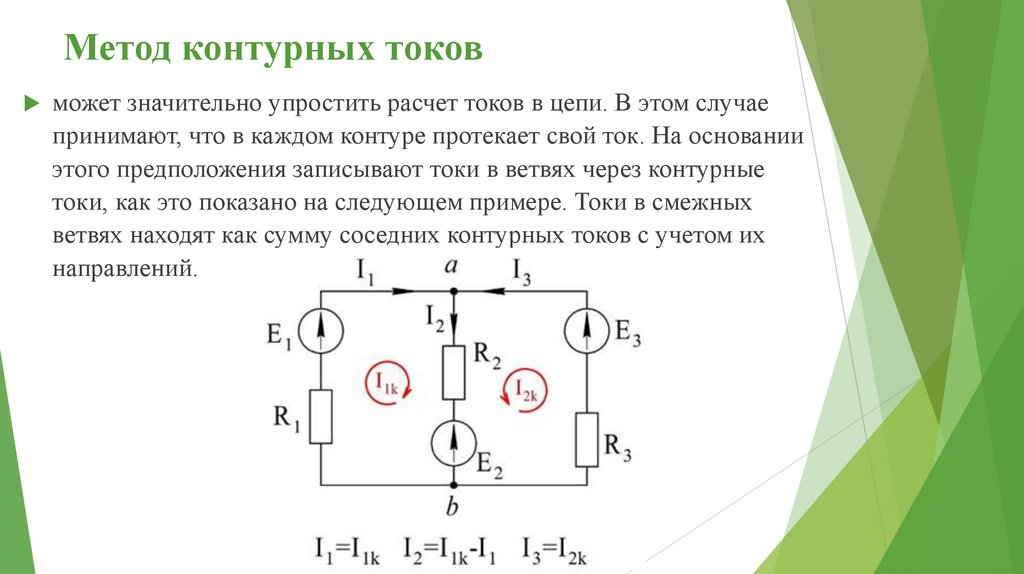
Метод контурных токов
может значительно упростить расчет токов в цепи. В этом случае
принимают, что в каждом контуре протекает свой ток. На основании
этого предположения записывают токи в ветвях через контурные
токи, как это показано на следующем примере. Токи в смежных
ветвях находят как сумму соседних контурных токов с учетом их
направлений.

12.

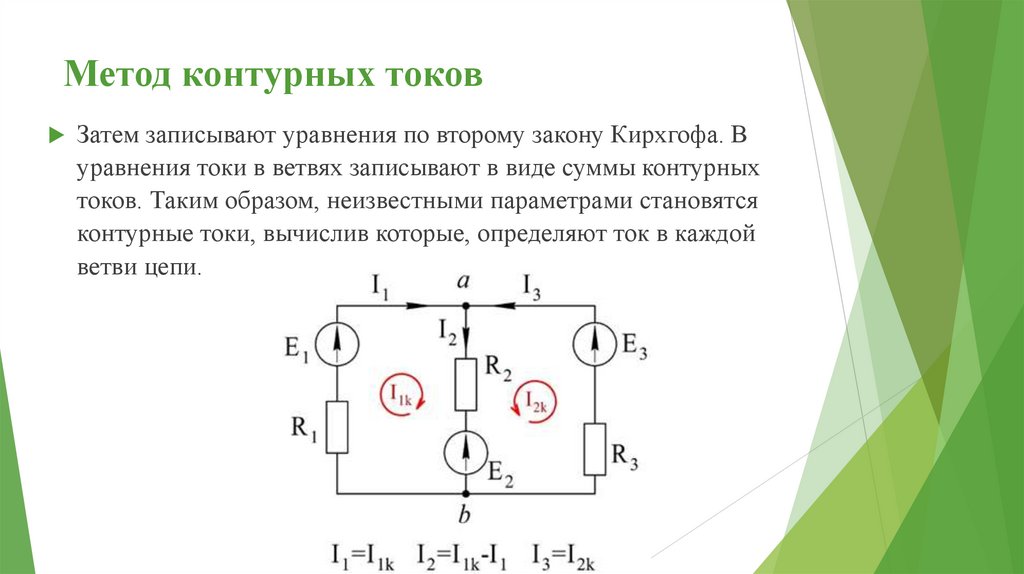
Метод контурных токов
Затем записывают уравнения по второму закону Кирхгофа. В
уравнения токи в ветвях записывают в виде суммы контурных
токов. Таким образом, неизвестными параметрами становятся
контурные токи, вычислив которые, определяют ток в каждой
ветви цепи.

13.

Метод узловых напряжений
(потенциалов)
Метод узловых напряжений используют в случае
сложных разветвленных цепей с небольшим числом
узлов. Узлы цепи нумеруют в произвольном порядке и
потенциал одного из узлов (чаще последнего)
принимают равным нулю. Составляют систему
уравнений и находят потенциалы в узлах цепи.
Находят напряжение в каждой ветви как разность
потенциалов двух смежных узлов. По напряжению
определяют токи в ветвях.

14.

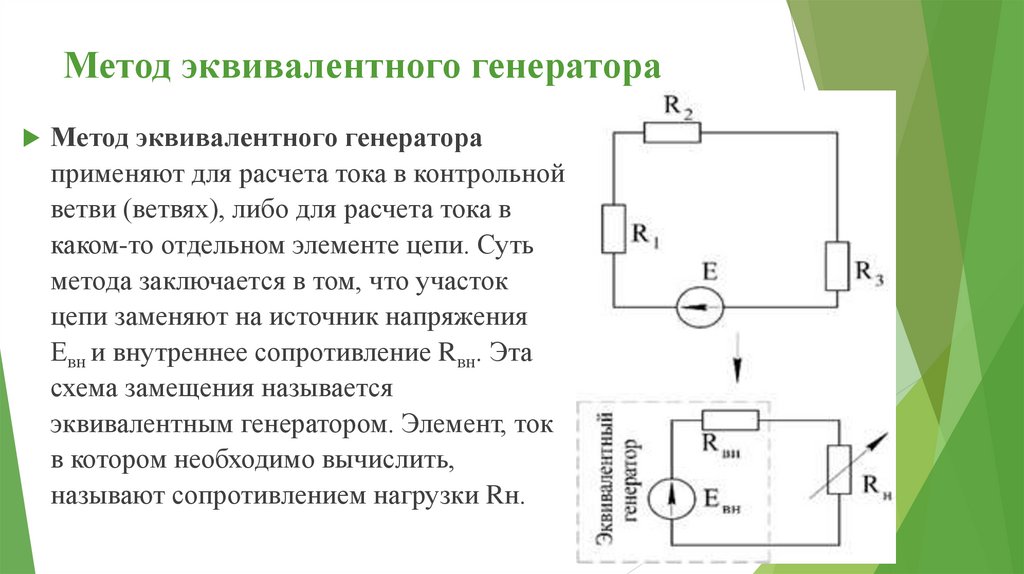
Метод эквивалентного генератора
Метод эквивалентного генератора
применяют для расчета тока в контрольной
ветви (ветвях), либо для расчета тока в
каком-то отдельном элементе цепи. Суть
метода заключается в том, что участок
цепи заменяют на источник напряжения
Евн и внутреннее сопротивление Rвн. Эта
схема замещения называется
эквивалентным генератором. Элемент, ток
в котором необходимо вычислить,
называют сопротивлением нагрузки Rн.

15.

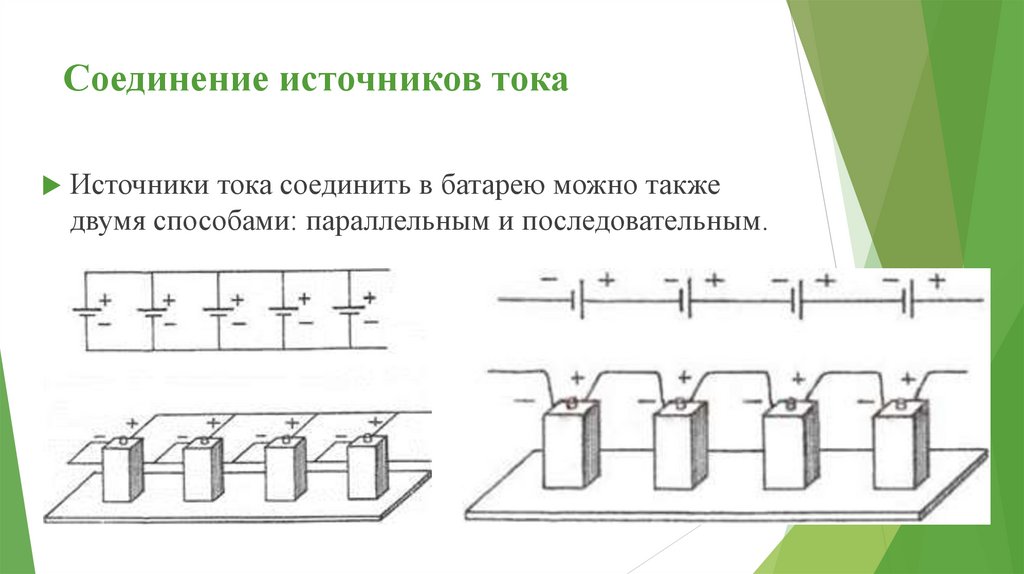
Соединение источников тока
Источники тока соединить в батарею можно также
двумя способами: параллельным и последовательным.

16.

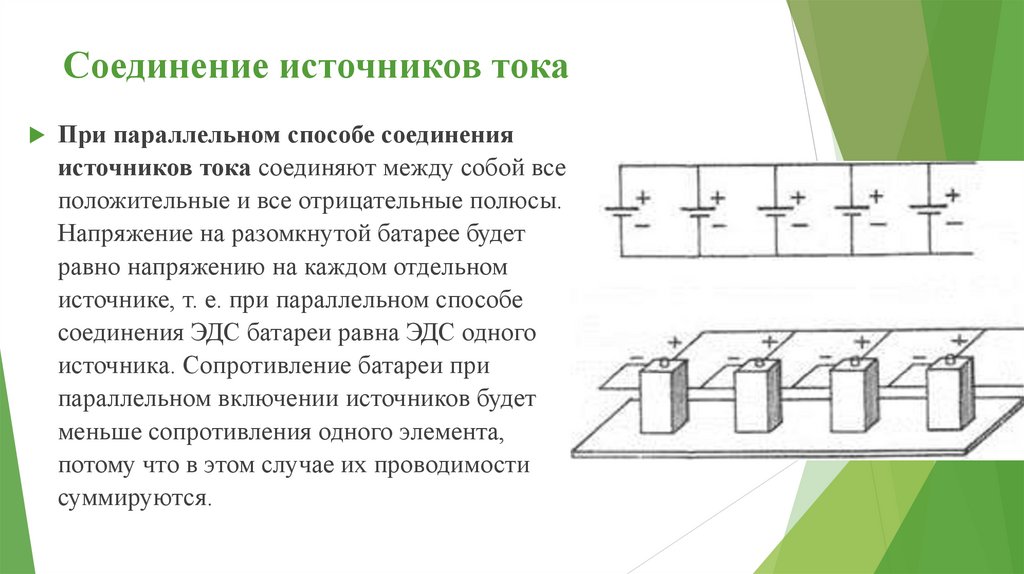
Соединение источников тока
При параллельном способе соединения
источников тока соединяют между собой все
положительные и все отрицательные полюсы.
Напряжение на разомкнутой батарее будет
равно напряжению на каждом отдельном
источнике, т. е. при параллельном способе
соединения ЭДС батареи равна ЭДС одного
источника. Сопротивление батареи при
параллельном включении источников будет
меньше сопротивления одного элемента,
потому что в этом случае их проводимости
суммируются.

17.

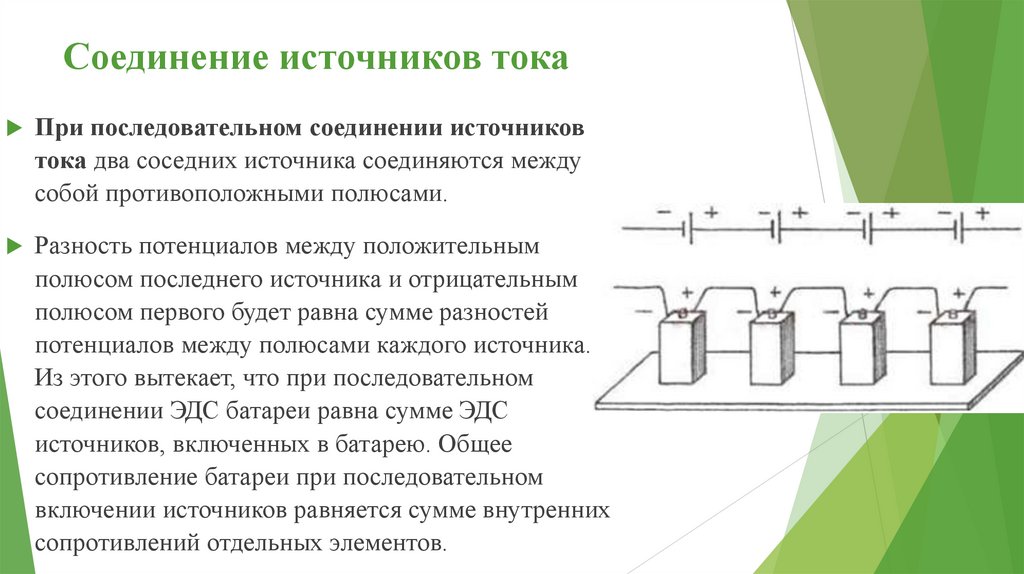
Соединение источников тока
При последовательном соединении источников
тока два соседних источника соединяются между
собой противоположными полюсами.
Разность потенциалов между положительным
полюсом последнего источника и отрицательным
полюсом первого будет равна сумме разностей
потенциалов между полюсами каждого источника.
Из этого вытекает, что при последовательном
соединении ЭДС батареи равна сумме ЭДС
источников, включенных в батарею. Общее
сопротивление батареи при последовательном
включении источников равняется сумме внутренних
сопротивлений отдельных элементов.

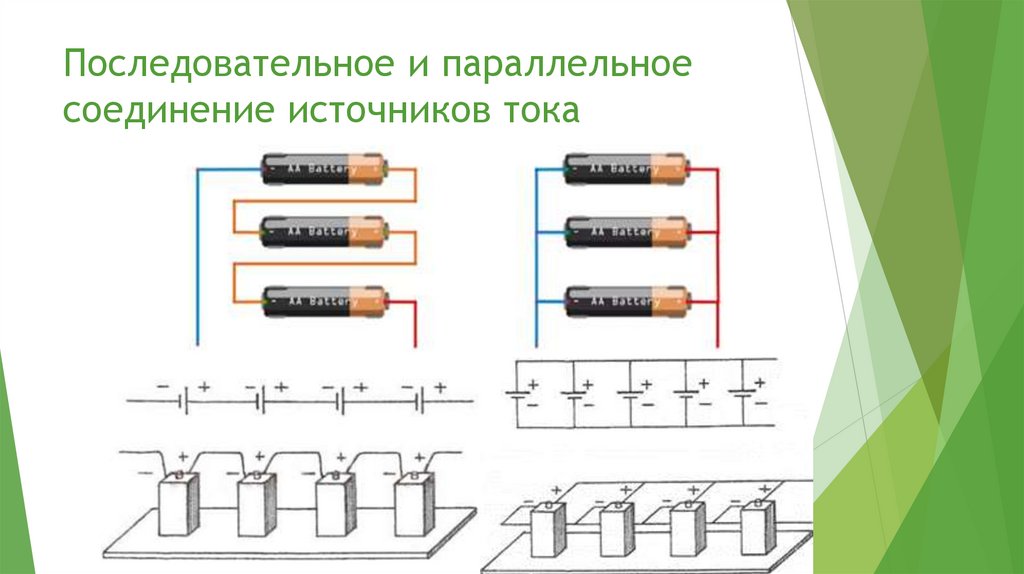
18.

Последовательное и параллельное
соединение источников тока

19.

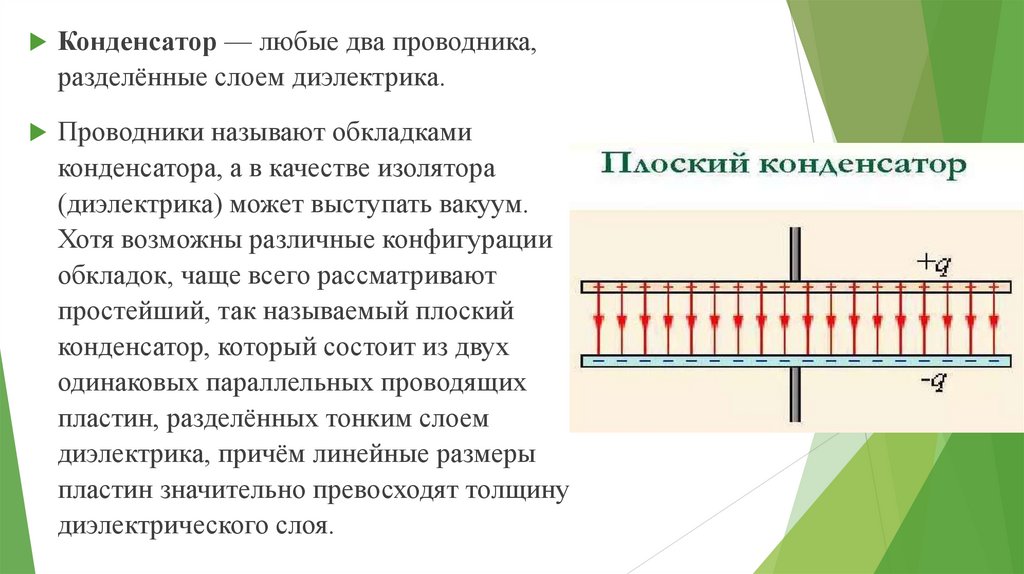
Конденсатор — любые два проводника,
разделённые слоем диэлектрика.
Проводники называют обкладками
конденсатора, а в качестве изолятора
(диэлектрика) может выступать вакуум.
Хотя возможны различные конфигурации
обкладок, чаще всего рассматривают
простейший, так называемый плоский
конденсатор, который состоит из двух
одинаковых параллельных проводящих
пластин, разделённых тонким слоем
диэлектрика, причём линейные размеры
пластин значительно превосходят толщину
диэлектрического слоя.

20.

Существуют два способа классифицировать
конденсаторы:
по виду диэлектрика: твёрдые, жидкие,
газообразные;
по форме обкладок: плоские, сферические,
цилиндрические.

21.

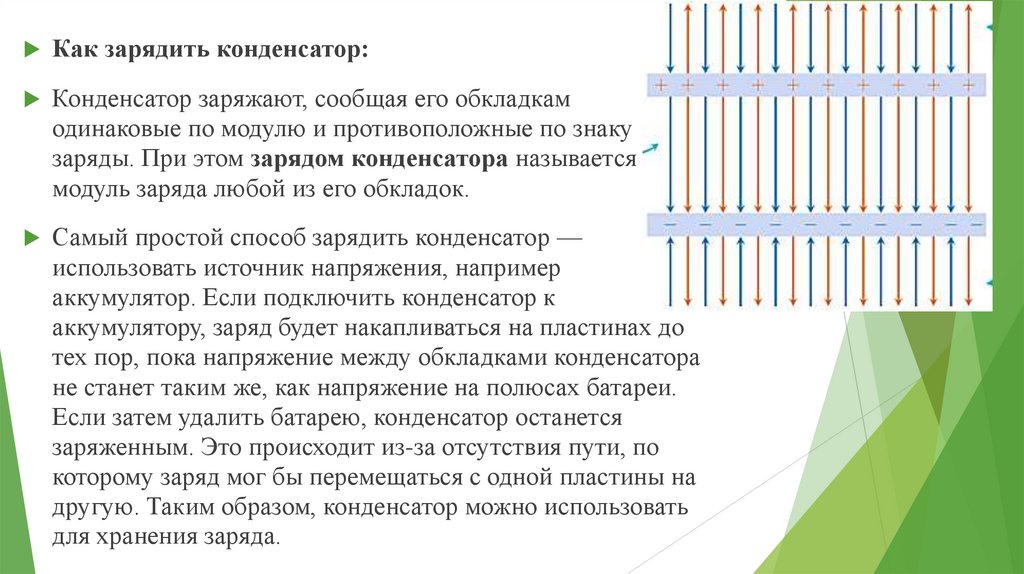
Как зарядить конденсатор:
Конденсатор заряжают, сообщая его обкладкам
одинаковые по модулю и противоположные по знаку
заряды. При этом зарядом конденсатора называется
модуль заряда любой из его обкладок.
Самый простой способ зарядить конденсатор —
использовать источник напряжения, например
аккумулятор. Если подключить конденсатор к
аккумулятору, заряд будет накапливаться на пластинах до
тех пор, пока напряжение между обкладками конденсатора
не станет таким же, как напряжение на полюсах батареи.
Если затем удалить батарею, конденсатор останется
заряженным. Это происходит из-за отсутствия пути, по
которому заряд мог бы перемещаться с одной пластины на
другую. Таким образом, конденсатор можно использовать
для хранения заряда.

22.

23.

Свойство конденсаторов накапливать электрический заряд
характеризуется электроёмкостью. Заряд конденсатора
прямо пропорционален напряжению между его обкладками.
Коэффициент пропорциональности и называется
электрической ёмкостью конденсатора.
Электрическая ёмкость конденсатора — физическая
величина, равная отношению заряда на одной из его пластин к
напряжению между пластинами:
Единица электрической ёмкости в СИ — фарад; 1 Ф = 1 Кл/1В.

24.

От чего зависит электроёмкость конденсатора:
1. Чем больше площадь пластин конденсатора, тем
больше его электроёмкость.
2. Чем больше расстояние между пластинами
конденсатора, тем меньше его электроёмкость.
3. При заполнении пространства между обкладками
конденсатора диэлектриком его электроёмкость
увеличивается.

25.

Определение энергии электрического поля
конденсатора:
Способность конденсатора накапливать
электрическую энергию обусловливает его
практическую значимость в электронных устройствах.
Энергия электрического поля конденсатора
пропорциональна квадрату заряда, накопленного на
одной из его обкладок.

26.

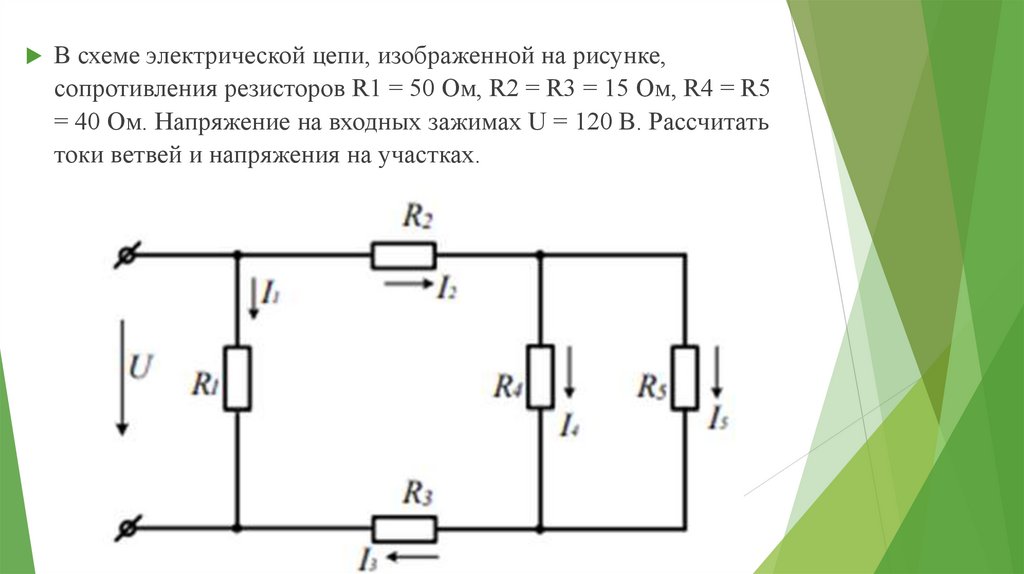
В схеме электрической цепи, изображенной на рисунке,
сопротивления резисторов R1 = 50 Ом, R2 = R3 = 15 Ом, R4 = R5
= 40 Ом. Напряжение на входных зажимах U = 120 B. Рассчитать
токи ветвей и напряжения на участках.