Решение логических задач. Часть 2

1.

Решение логических задач.
Часть 2.
Самсон
Павел
Иванович,
главный
́ ов
методист Московского центра непрерывного
математического образования
21 января 2025

2.

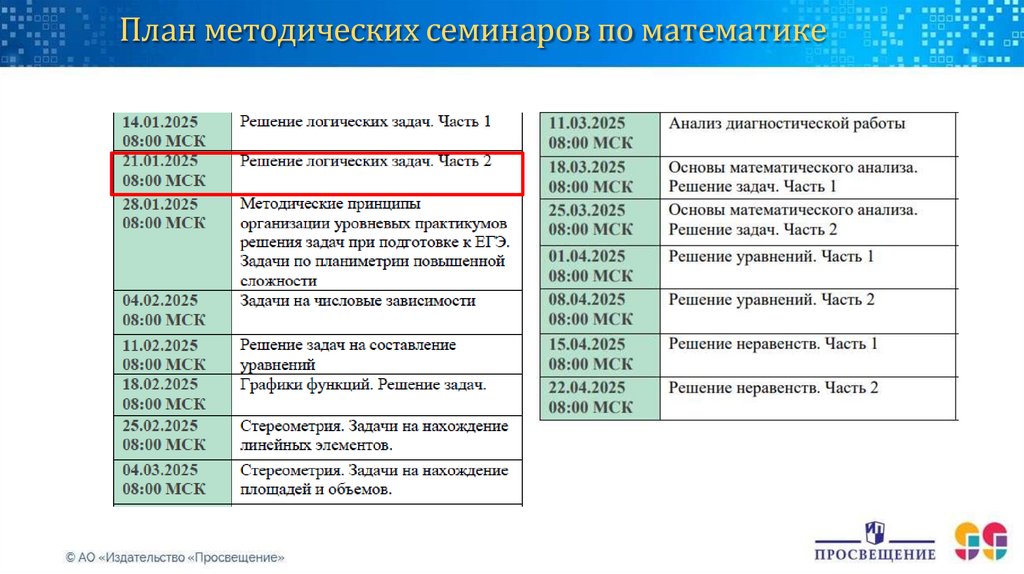
План методических семинаров по математике

3.

Достоверный источник информации
открытый банк заданий
открытые варианты
методические
рекомендации на основе
анализа ошибок
материалы для
предметных комиссий

Домашнее задание
С трёхзначным числом производят следующую операцию: вычитают из него
сумму его цифр, а затем получившуюся разность делят на 3.
а) Могло ли в результате такой операции получиться число 300?
б) Могло ли в результате такой операции получиться число 151?
в) Сколько различных чисел может получиться в результате такой операции
из чисел от 100 до 600 включительно?
Решение.
а) Сумма цифр числа 910 равна 10. Следовательно, в результате операции
из этого числа получится 910 10 300.
3
б) Пусть число равно 100a 10b c , где a , b и c — цифры и a 0 . Тогда
сумма цифр такого числа равна a b c , а в результате операции из него
100a 10b c a b c 33a 3b.
получится число
Получившееся
3
число делится на 3. Следовательно, число 151 не могло получиться.

8.

Домашнее задание
С трёхзначным числом производят следующую операцию: вычитают из него сумму его
цифр, а затем получившуюся разность делят на 3.
а) Могло ли в результате такой операции получиться число 300?
Решение.
а) Пусть число равно 100a 10b c , где a , b и c — цифры и a 0 . Тогда сумма цифр
такого числа равна a b c , а в результате операции из него получится число
100a 10b c a b c 33a 3b .
3
33a 3b 300, 11a b 100,
a 9 и b 1.
Сумма цифр числа 910 равна 10. Следовательно, в результате операции из этого числа
получится 910 10 300.
3

9.

Домашнее задание
С трёхзначным числом производят следующую операцию: вычитают из него сумму его
цифр, а затем получившуюся разность делят на 3.
б) Могло ли в результате такой операции получиться число 151?
Решение.
б) Пусть число равно 100a 10b c , где a , b и c — цифры и a 0 . Тогда сумма цифр
такого числа равна a b c , а в результате операции из него получится число
100a 10b c a b c 33a 3b. Получившееся число делится на 3.
3
Следовательно, число 151 не могло получиться.

10.

11.

Домашнее задание
Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все
возможные суммы (по 2, по 3 и т. д.) выписывают на доску в порядке неубывания. Если
какое-то число n, выписанное на доску, повторяется несколько раз, то на доске
оставляется одно такое число n, а остальные числа, равные n, стираются. Например,
если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
б) Существует ли пример таких задуманных чисел, для которых на доске будет
записан набор 1, 3, 4, 5, 6, 9, 10, 11, 12, 13, 14, 17, 18, 19, 20, 22?
Решение.
б) Задуманные числа – натуральные, значит, наименьшее число в наборе – это
наименьшее из задуманных чисел, а наибольшее число в наборе – это сумма всех
задуманных чисел. Среди чисел записанного набора должна быть сумма всех чисел,
кроме наименьшего, то есть 22 – 1 = 21. Но этого числа нет в наборе, поэтому не
существует примера таких задуманных чисел, для которого на доске будет выписан
приведенный набор.

12.

Домашнее задание
На доске написано 10 различных натуральных чисел. Среднее арифметическое шести
наименьших из них равно 6, а среднее арифметическое шести наибольших равно 12.
а) Может ли наибольшее из этих десяти чисел равняться 14?
Решение.
а) Если наибольшее число равно 14, то сумма шести наибольших
не больше 14 13 12 11 10 9 69 , а их среднее арифметическое меньше 12.
чисел

13.

Домашнее задание
На доске написано 10 различных натуральных чисел. Среднее арифметическое шести
наименьших из них равно 6, а среднее арифметическое шести наибольших равно 12.
б) Может ли среднее арифметическое всех десяти чисел равняться 8,4?
Решение.
б) Пусть сумма четырёх наименьших чисел равна A , сумма пятого и шестого по
величине чисел равна B , а сумма четырёх наибольших чисел равна C . Предположим,
что среднее арифметическое всех десяти чисел равно 8,4. Тогда получаем:
A B 36 , B C 72 , A B C 84 ,
откуда B 24 , C 48 . Это невозможно, поскольку должно выполняться неравенство
C 2B .

14.

Домашнее задание
В школах №1 и №2 учащиеся писали тест. Из каждой школы тест писали
по крайней мере 2 учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся,
писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе
средний балл за тест был целым числом. После этого один из учащихся, писавших тест,
перешёл из школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих
школах.
а) Мог ли средний балл в школе №1 вырасти в 2 раза?
Решение.
а) Пусть в школе №1 писали тест n учащихся, а средний балл равнялся A . Тогда
суммарный балл всех учащихся этой школы равнялся nA , а после перехода одного
учащегося в школу №2 суммарный балл стал равняться 2 n 1 A. Таким образом,
суммарный балл уменьшился на 2 n A , что невозможно, поскольку перешедший
учащийся набрал положительное количество баллов, а n 2.

15.

Домашнее задание
В школах №1 и №2 учащиеся писали тест. Из каждой школы тест писали
по крайней мере 2 учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся,
писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе
средний балл за тест был целым числом. После этого один из учащихся, писавших тест,
перешёл из школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих
школах.
б) Средний балл в школе №1 вырос на 10%, средний балл в школе №2 также вырос
на 10%. Мог ли первоначальный средний балл в школе №2 равняться 1?
Решение.
б) Пусть в школе №2 средний балл равнялся B , а перешедший в неё учащийся набрал
u баллов. Тогда получаем:
u nA 1,1 n 1 A 1,1 52 n B 51 n B ; 10u 11 n A 62 n B .
Если B 1, то n 2, поскольку число 62 n B должно делиться на 10,
а 11 n A не должно быть отрицательным. Получаем 9 A 60, что невозможно,
поскольку A целое.

16.

Домашнее задание

17.

Домашнее задание

English Русский Rules