Первые учения о формах и способах рассуждений возникли в странах Древнего Востока

1.

Первые учения
о формах и
способах
рассуждений
возникли
в странах
Древнего
Востока
(Китай, Индия)

2.

В основе современной
логики лежат учения,
созданные древнегреческими
мыслителями (Аристотель, Геродот)
Аристотель 384-322 до н.э
Геродот ок 490-425 до н.э

3.

АРИФМЕТИКОЛОГИЧЕСКИЕ ОСНОВЫ
РАБОТЫ КОМПЬЮТЕРА

4.

Логика – наука
Логика — это наука о формах и способах мышления. Это
учение о способах рассуждений и доказательств.
Законы мышления
отражают в сознании человека
свойства, связи и отношения
объектов окружающего мира

5.

Понятие
Высказывание
Умозаключение
— это форма мышления,
которая выделяет
существенные признаки
предмета или класса
предметов, позволяющие
отличать их от других.
— это формулировка своего
— это форма мышления, с
понимания окружающего
помощью которой из одного
мира. Высказывание является
или нескольких суждений
повествовательным
может быть получено новое
предложением, в котором чтосуждение (знание или
либо утверждается или отрицается.
вывод).
Пример :
Прямоугольник, проливной
дождь, компьютер
Истинным будет высказывание, в
котором связь понятий правильно
отражает свойства и отношения
реальных вещей 1 (true).
Ложным высказывание будет в том
случае, когда оно противоречит
реальной действительности
0 (false).
Пример:
«Буква «а» — гласная» - истинное
высказывание.
«Компьютер был изобретён в
середине 19 века» - ложное
высказывание.
Пример
Дано высказывание: «Все
углы равнобедренного
треугольника равны».
Получите высказывание
«Этот треугольник
равносторонний» путём
умозаключений.

6.

Задание
Какие из предложений являются высказываниями?
Определите их истинность.
1. Какой длины эта лента?
2. Париж — столица Англии.
3. Число 11 является простым.
4. Делайте утреннюю зарядку!
5. 4 + 5 = 10
6. Без труда не вытащишь и рыбку из пруда.
7. Некоторые медведи живут на севере.
8. Все медведи — бурые.

7.

Алгебра логики - наука
Работу компьютера описывает
алгебра логики. Ее основал
английский математик и логик
Джордж Буль, поэтому ее также
называет булевой алгеброй.
Джордж Буль
(1815 — 1864)
Алгебра логики — это наука об
общих операциях, аналогичных сложению
и умножению, которые выполняются
над высказываниями.

8.

Логические термины
Логическая переменная — это простое высказывание, содержащее
только одну мысль. Её символическое обозначение — латинская буква
(например, A, B, X, Y и т. д.)
Составное высказывание — логическая функция, которая содержит
несколько простых мыслей, соединённых между собой с помощью
логических операций. Её символическое обозначение — F(A, B,…).
На основе простых высказываний могут быть построены составные
высказывания.
Логические операции — логическое действие.
Таблица истинности — таблица, определяющая значение сложного
высказывания при всех возможных значениях простых высказываний.

9.

ЛОГИЧЕСКИЕ
ОПЕРАЦИИ

10.

Инверсия
Инверсия – логическое отрицание, при котором каждому
простому высказыванию ставится в соответствие новое
высказывание, значение которого противоположно
исходному.
Образуется
путем
добавления
противопоставления «Неверно, что …».
Обозначения: НЕ; ¬; ¯
Таблица истинности
Графическое представление

11.

Конъюнкция
Конъюнкция – логическое умножение (союз и), при
котором составное высказывание истинно тогда и только
тогда, когда истинны все входящие в него простые
высказывания.
Обозначения: ∧; &; ∙
Таблица истинности
Графическое представление

12.

Дизъюнкция
Дизъюнкция – логическое сложение (союз или), при
котором составное высказывание ложно тогда и только
тогда, когда ложны все входящие в него простые
высказывания.
Обозначения: ∨; ⎢; +
Таблица истинности
Графическое представление

13.

Импликация
Импликация – логическое следование, образуется
соединением двух высказываний в одно с помощью
оборота речи «Если…, то…», при котором составное
высказывание ложно тогда и только тогда, когда из
истинного высказывания следует ложное.
Обозначения: → ; ⇒
Таблица истинности
Графическое представление

14.

Эквивалентность
Эквивалентность (равнозначность, тождественность) –
новое высказывание, которое истинно тогда и только
тогда, когда оба исходных высказывания одновременно
истинны, либо ложны.
В естественном языке: «А тогда и только тогда, когда В».
Обозначения: ↔; ≡; ∼
Таблица истинности
Графическое представление

15.

Порядок выполнения
логических операций
При составлении логического выражения необходимо
учитывать порядок выполнения логических операций,
а именно:
1.
2.
3.
4.
5.
6.
Действия в скобках;
Инверсия (отрицание);
Конъюнкция (умножение);
Дизъюнкция (сложение);
Импликация (следствие);
Эквивалентность (тождество).

16.

Найти значения
логических выражений:
1) F = (0 ٧ 0 ) ٧ (1 ٧ 1) =0+1=1
2) F = (1 ٧ 1 ) ٧ (1 ٧ 0) =1+1=1
3) F = (0 & 0 ) & (1 & 1) = 0*1=0
4) F = ¬ 1 & (1 ٧ 1 ) ٧ (¬ 0 & 1) =0*1+1=1
5) F = (¬ 1٧ 1 ) & (1 ٧ ¬ 1 ) & (¬ 1 ٧ 0) =1*1*0=0

17.

Составить и записать истинные сложные
высказывания из простых с
использованием логических операций:
1) А является max (A,B,C)
(A>B) ∧ (A>C)
2) Любое из чисел X,Y,Z положительно
(X>0) ∨ (Y>0) ∨ (Z>0)
3) Любое из чисел X,Y,Z отрицательно
(X<0) ∨ (Y<0) ∨ (Z<0)
4) Все числа X,Y,Z равны 12
(X=12) ∧ (Y=12) ∧ (Z=12)

18.

АЛГОРИТМ
СОСТАВЛЕНИЯ ТАБЛИЦ
ИСТИННОСТИ ДЛЯ СЛОЖНЫХ
ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ

19.

20.

Шаг 1:
Определить количество строк в таблице:
Количество строк =
+1
где n – количество логических переменных в выражении
«+1» – одна строка для шапки таблицы
Количество переменных – 3 (А, В, С)
поэтому Количество строк =
+1=9

21.

Шаг 2:
Определить количество столбцов в таблице:
Количество столбцов =
=количество переменных + количество операций
Количество переменных – 3 (А, В, С)
Количество операций 5 – 2 инверсии, 2 конъюнкции, 1
дизъюнкции
поэтому Количество столбцов = 3+5=8

22.

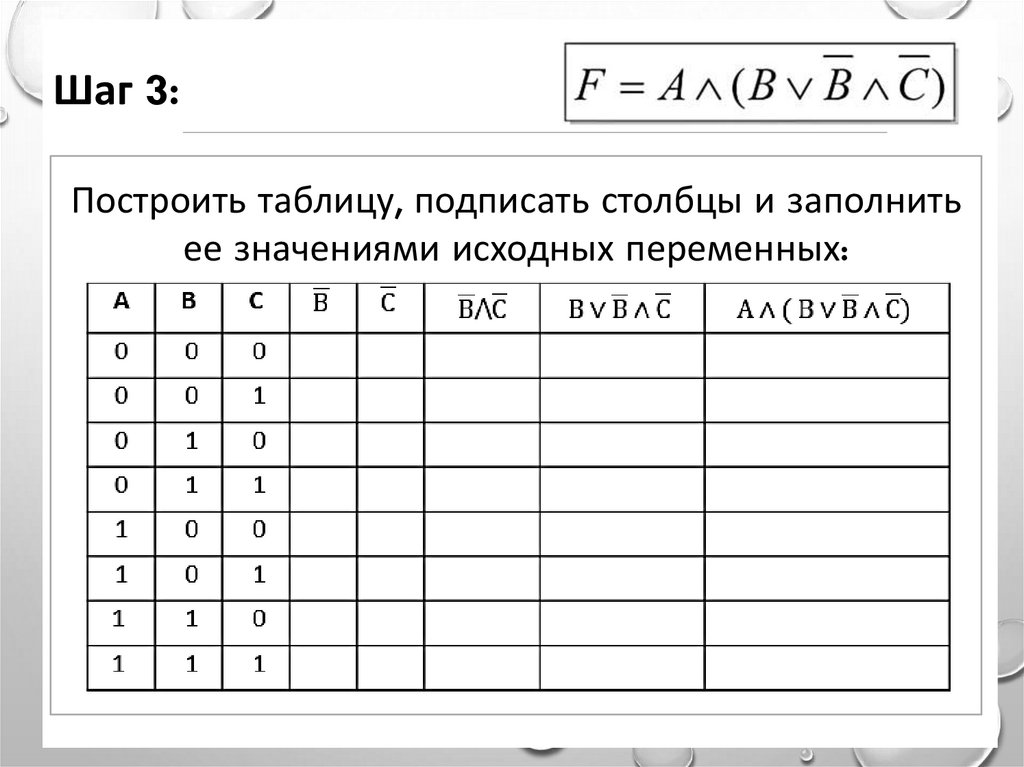
Шаг 3:
Построить таблицу, подписать столбцы и заполнить
ее значениями исходных переменных:

23.

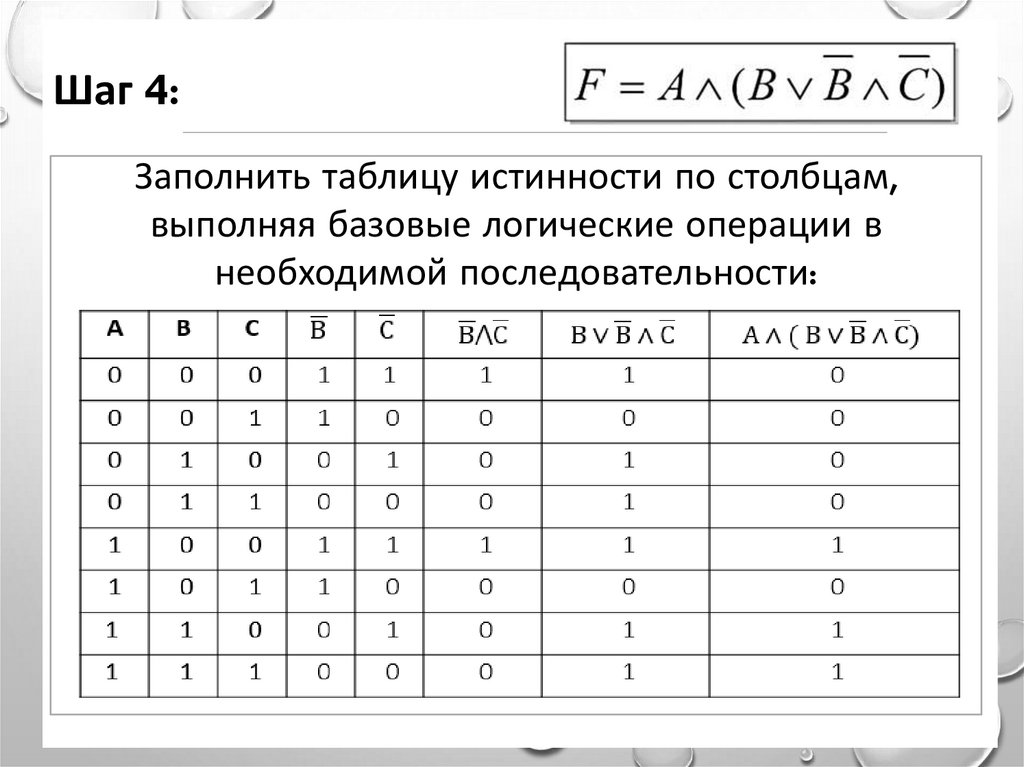
Шаг 4:
Заполнить таблицу истинности по столбцам,
выполняя базовые логические операции в
необходимой последовательности:

24.

Пример:
Запишите в виде логического выражения следующее высказывание:
«Летом Петя поедет в деревню и, если будет хорошая погода, то он пойдёт на
рыбалку».
• Проанализируем составное высказывание.
• Оно состоит из следующих простых высказываний:
«Петя поедет в деревню»,
«Будет хорошая погода»,
«Он пойдёт на рыбалку».
• Обозначим их через логические переменные:
А = Петя поедет в деревню;
В = Будет хорошая погода;
С = Он пойдёт на рыбалку.
• Запишем высказывание в виде логического выражения, учитывая порядок
действий. Если необходимо, расставим скобки:
F = A ^ (B
C).

25.

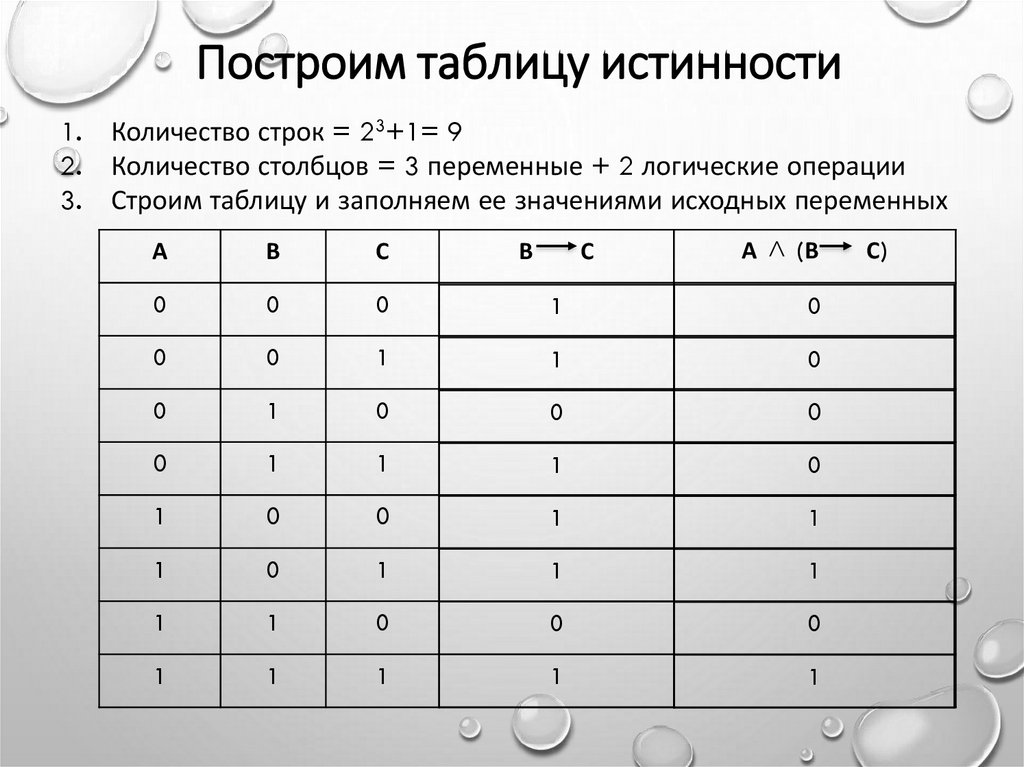
Построим таблицу истинности
1.
2.
3.
Количество строк = 23+1= 9
Количество столбцов = 3 переменные + 2 логические операции
Строим таблицу и заполняем ее значениями исходных переменных
В
С
А ∧ (В
А
В
С
0
0
0
1
0
0
0
1
1
0
0
1
0
0
0
0
1
1
1
0
1
0
0
1
1
1
0
1
1
1
1
1
0
0
0
1
1
1
1
1
С)

26.

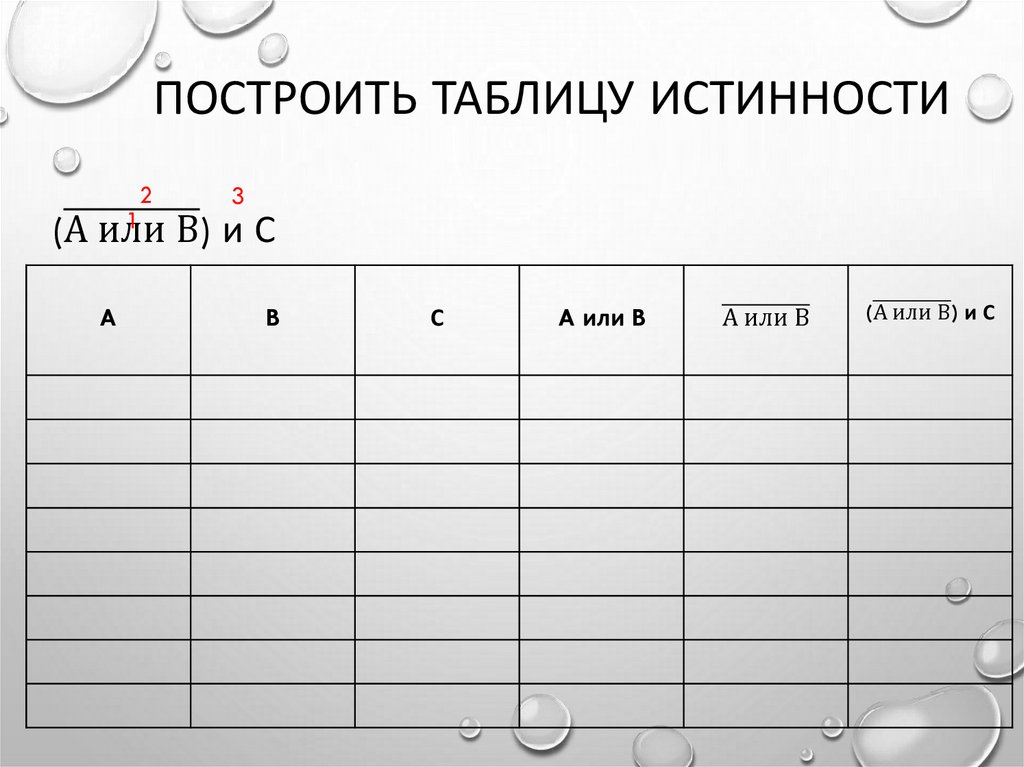
ПОСТРОИТЬ ТАБЛИЦУ ИСТИННОСТИ
2
1
3
(А или В) и С
A
B
С
A или B
А или В
(А или В) и С

27.

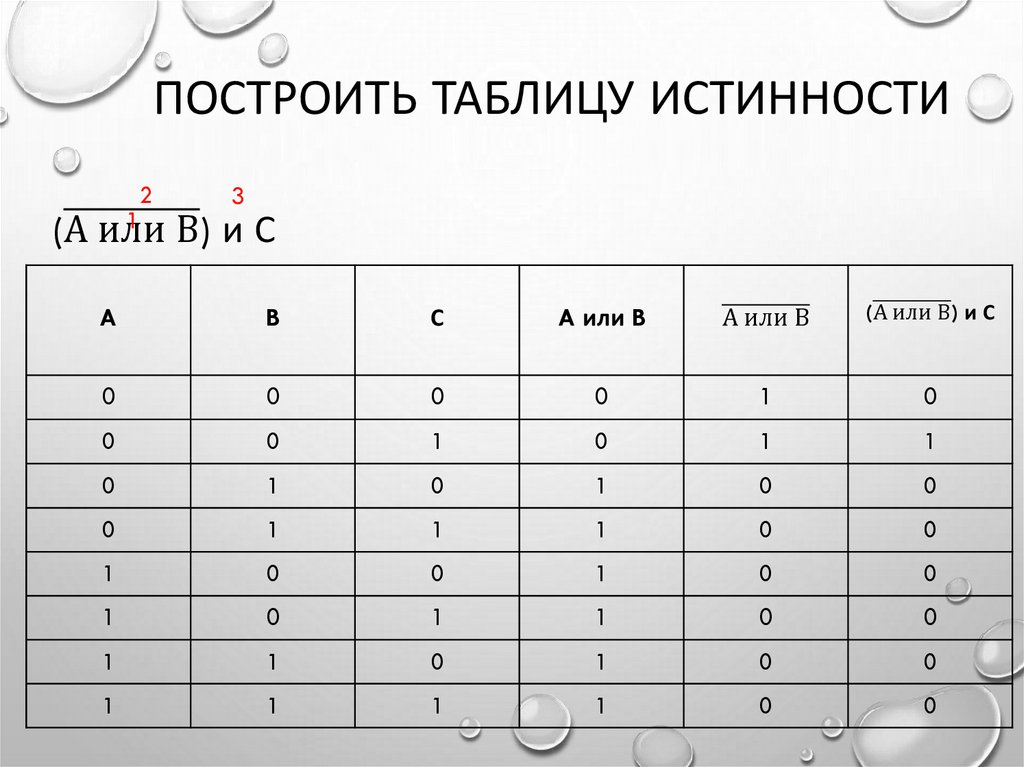
ПОСТРОИТЬ ТАБЛИЦУ ИСТИННОСТИ
2
1
3
(А или В) и С
A
B
С
A или B
А или В
(А или В) и С
0
0
0
0
1
0
0
0
1
0
1
1
0
1
0
1
0
0
0
1
1
1
0
0
1
0
0
1
0
0
1
0
1
1
0
0
1
1
0
1
0
0
1
1
1
1
0
0

28.

Благодарю за работу
на занятии!