Элементы алгебры логики. Математические основы информатики. Информатика и ИКТ

1.

ЭЛЕМЕНТЫ
АЛГЕРЫ ЛОГИКИ
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ

2.

Высказывание
Высказывание - это предложение на любом языке,
содержание которого можно однозначно определить как
истинное или ложное.
Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его
часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с
помощью логических операций.
Название логической операции
Логическая связка
Конъюнкция
«и»; «а»; «но»; «хотя»
Дизъюнкция
«или»
Инверсия
«не»; «неверно, что»

3.

Задание 1
Для какого из приведённых значений числа X ложно высказывание:
НЕ (X < 6) ИЛИ (X < 5)?
1) 7
2) 6
3) 5
4) 4
Задание 2 Для какого из приведённых чисел истинно высказывание:
НЕ (число <50) И (число чётное)?
1) 24
2) 45
3) 74
4) 99

4.

Задание 3 Для какого из приведённых наборов букв истинно высказывание:
НЕ (Первая буква согласная) И НЕ (Вторая буква гласная)?
1) Aabas
2) bcade
3) abcde
4) cabab

5.

Алгебра логики
Алгебра
логики
вычисления значений,
высказываний.
определяет
упрощения
правила
записи,
и преобразования
В алгебре логики высказывания обозначают буквами и
называют логическими переменными.
Если
высказывание
истинно,
то
значение
соответствующей ему логической переменной обозначают
единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями.

6.

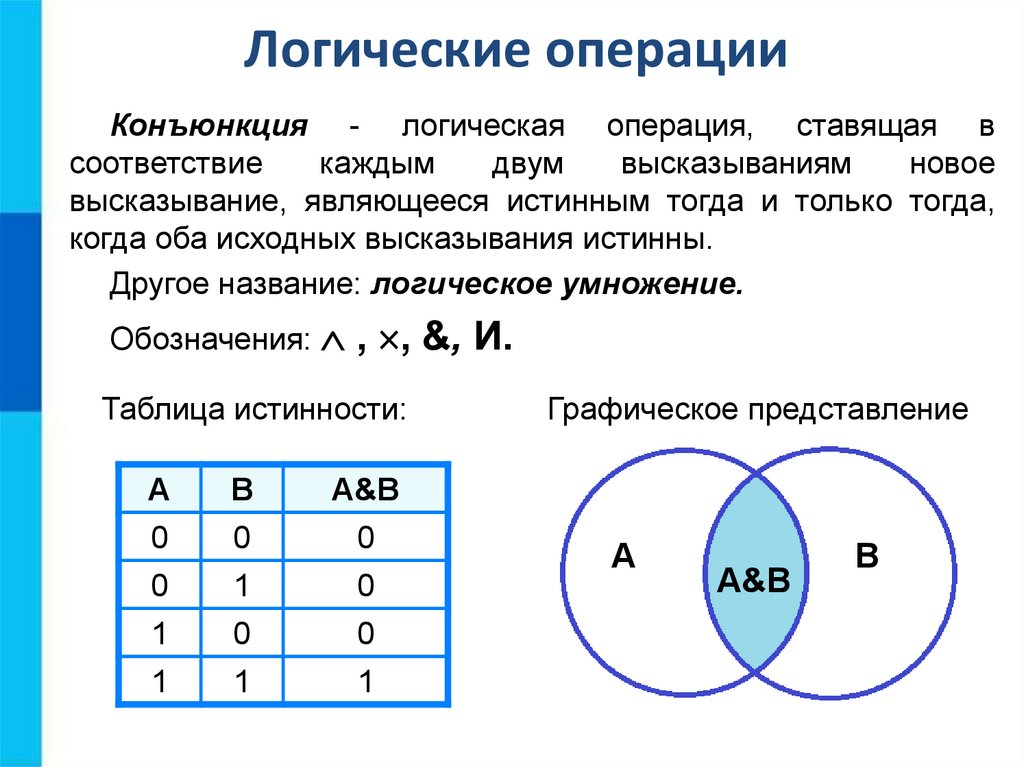
Логические операции
Конъюнкция - логическая операция, ставящая в
соответствие
каждым
двум
высказываниям
новое
высказывание, являющееся истинным тогда и только тогда,
когда оба исходных высказывания истинны.
Другое название: логическое умножение.
Обозначения: , , &, И.
Таблица истинности:
А
В
А&В
0
0
0
0
1
0
1
0
0
1
1
1
Графическое представление
A
А&В
B

7.

Логические операции
Дизъюнкция - логическая операция, которая каждым двум
высказываниям ставит в соответствие новое высказывание,
являющееся ложным тогда и только тогда, когда оба исходных
высказывания ложны.
Другое название: логическое сложение.
Обозначения: V, |,
ИЛИ, +.
Таблица истинности:
А
В
АVВ
0
0
0
0
1
1
1
0
1
1
1
1
Графическое представление
A
B
АVВ

8.

Логические операции
Инверсия - логическая операция, которая каждому
высказыванию ставит в соответствие новое высказывание,
значение которого противоположно исходному.
Другое название: логическое отрицание.
Обозначения: НЕ,
¬,¯ .
Таблица истинности:
А
Ā
0
1
1
0
Графическое представление
Ā
A
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция.

9.

10.

11.

Решение задач
Дан фрагмент таблицы истинности выражения F:
x1
x2
x3
x4
x5
x6
F
1
1
0
0
0
0
0
1
0
1
0
0
1
0
1
0
0
1
0
0
0
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)

12.

Решение задач
Логическая функция F задаётся выражением (x → y) ∧ (y → z). На рисунке
приведён фрагмент таблицы истинности функции F. Определите, какому
столбцу таблицы истинности функции F соответствует каждая из
переменных x, y, z.
Перем. 1
Перем. 2
Перем. 3
Функция
???
1
1
???
1
0
???
0
0
F
1
1
В ответе напишите буквы x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу, затем – буква, соответствующая второму столбцу, и т. д.).

13.

Решение задач
Логическая функция F задаётся выражением (x ∨ y) → (z ≡ x).
Дан
частично
заполненный
фрагмент,
содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из
переменных x, y, z.
Переменная 1 Переменная 2 Переменная 3
???
Функция
???
???
F
0
0
0
0
0
В ответе напишите буквы x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу, затем – буква, соответствующая второму столбцу, и т. д.).