Лекции по теоретической механике. Статика

1. Лекции по теоретической механике

Статика

2. Литература (библиотека БФ ПНИПУ)

Яблонский, А.А. Курс теоретической механики / А.А.
Яблонский, В.М. Никифорова. – М.: Интеграл-Пресс,
2007. – 608 с.
Тарг, С.М. Краткий курс теоретической механики /
С.М. Тарг. – М.: Высш. шк., 2009. – 416 с.
Сборник заданий для курсовых работ по
теоретической механике / под общ. ред. А.А.
Яблонского. – М.: КНОРУС, 2011. – 392 с.

3. Литература (ЭБС Лань)

Диевский, В. А. Теоретическая механика : учебник для вузов / В. А. Диевский. —
7-е изд., стер. — Санкт-Петербург : Лань, 2024. — 348 с. — ISBN 978-5-50751525-7. — Текст : электронный // Лань : электронно-библиотечная система. —
URL: https://e.lanbook.com/book/422627
Доронин, Ф. А. Теоретическая механика : учебное пособие / Ф. А. Доронин. —
Санкт-Петербург : Лань, 2022. — ISBN 978-5-8114-2585-3. — Текст :
электронный // Лань : электронно-библиотечная система. — URL:
https://e.lanbook.com/book/212570
Мещерский, И. В. Задачи по теоретической механике : учебное пособие / И. В.
Мещерский ; под редакцией В. А. Пальмова, Д. Р. Меркина. — 52-е изд., стер. —
Санкт-Петербург : Лань, 2022. — ISBN 978-5-8114-4190-7. — Текст :
электронный // Лань : электронно-библиотечная система. — URL:
https://e.lanbook.com/book/206417
Валькова, Т. А. Теоретическая механика : учебное пособие / Т. А. Валькова, А.
Е. Митяев, С. Г. Докшанин. — Красноярск : СФУ, 2020. — ISBN 978-5-7638-41558. — Текст : электронный // Лань : электронно-библиотечная система. — URL:
https://e.lanbook.com/book/181551

4. Содержание

1. Введение. Основные понятия статики. Аксиомы статики. Связи и
реакции связей.
2. Система сходящихся сил. Теорема о равновесии трех
непараллельных сил. Аналитическое определение
равнодействующей сходящихся сил. Уравнения равновесия.
3. Произвольная плоская система сил. Момент силы относительно
точки. Пара сил. Теоремы о парах. Метод Пуансо. Главный вектор и
главный момент. Уравнения равновесия. Три формы уравнений
равновесия. Теорема Вариньона.

5. Тема 1

Введение
Под названием “механика” объединяется ряд наук, изучающих механическое движение и механическое взаимодействие твердых и
деформируемых тел, а также жидких и газообразных сред.
Механика
Прикладная механика
Гидромеханика
Аэромеханика
Динамика сооружений
Механика корабля
Строительная механика
Строительные конструкции
Сопротивление материалов
Гидродинамика
Детали машин
Небесная механика
Механика грунтов
Мосты и тоннели
Теория механизмов и машин
Теоретическая механика
.
Теоретическая механика – это наука, в которой изучаются общие законы механического движения и механического взаимодействия
материальных тел.
Общность законов, пригодность для любых тел и систем, достигается абстрагированием от несущественных особенностей
рассматриваемого тела и выделением наиболее важных особенностей. Именно поэтому теоретическая механика является базовой
наукой, на основе которой изучаются другие прикладные технические дисциплины.
Механическое движение – это изменение с течением времени взаимного положения материальных точек в пространстве.
Механическое взаимодействие – это взаимодействие материальных тел, которое изменяет или стремится изменить характер их
механического движения.
Основные абстрактные образы (модели) материальных тел и систем:
Материальная точка (МТ) – это материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать.
МТ обладает массой и способностью взаимодействовать с другими телами.
Механическая система (МС) – совокупность МТ, в которой положение и движение каждой точки зависят от положения и движения других точек
этой системы.
Абсолютно твердое тело (АТТ) – это тело, в котором расстояния между любыми точками остаются неизменными.
В зависимости от условия задачи и выбора объекта изучения одно и то же физическое тело может быть принято за МТ, АТТ или МС.
Например, Земля при изучении ее движения вокруг Солнца принимается за МТ, а при изучении ее вращения вокруг собственной оси – за
АТТ. При изучении явлений, происходящих на Земле (приливы и отливы, перемещения коры и т.п.), Земля рассматривается как МС.
1

6. Тема 1

Теоретическая механика состоит из трех разделов:
Теоретическая механика
Статика
Кинематика
Динамика
Статика – это раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия
равновесия сил, приложенных к телу.
Кинематика – это раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с
силами, определяющими это движение.
Динамика – это раздел механики, в котором изучается движение материальных тел в пространстве в зависимости от действующих на них сил.
■ Основные понятия статики
Сила – мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия.
Сила определяется числовым значением (модулем), направлением и точкой приложения.
Сила изображается вектором. Прямая, по которой направлена сила, называется линией действия силы.
Р1
Р2
Система сил – совокупность нескольких сил, действующих на данное тело.
Эквивалентные системы сил – это системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом
состоянии.
Кинематическое состояние тела – это состояние покоя или движения определенного характера твердого тела.
Равнодействующая сила – это сила, эквивалентная системе сил.
Уравновешивающая сила – это сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону.
Система взаимно уравновешивающихся сил – это система сил, которая будучи приложенной к твердому телу, находящемуся в покое, не
выводит его из этого состояния.
Внешние силы – это силы, действующие на МТ данной системы со стороны МТ, не принадлежащих этой системе.
Внутренние силы – это силы взаимодействия между МТ рассматриваемой системы.
Основная задача статики – исследование условий равновесия внешних сил, приложенных к абсолютно твердому телу.
2

7. Тема 1

■
Аксиомы статики
1. Аксиома инерции
Под действием взаимно уравновешивающихся сил МТ находится в состоянии покоя или движется равномерно и прямолинейно.
2. Аксиома равновесия двух сил
Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны и если они направлены по
одной прямой в противоположные стороны.
Р1
Р1 Р 2
Р2
3. Аксиома присоединения и исключения уравновешивающихся сил
Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно
уравновешивающихся сил.
Р1
Р2
Р1
Р4
Р2
Р3
Р5
Р 4 Р5
( Р1 , Р 2 , Р 3 ) ( Р 1 , Р 2 , Р 3 , Р 4 , Р 5 )
Р3
Следствие из аксиомы присоединения и исключения уравновешивающихся сил : не изменяя кинематическое состояние АТТ, силу можно
переносить вдоль линии ее действия, сохраняя неизменными ее модуль и направление.
Р 2 Р3
Р1
Р1
Р2
Р3
Р1 Р3
Р2
( Р1 ) ( Р1 , Р 2 , Р 3 ) ( Р 2 )
2

8.

Тема1
4. Аксиома параллелограмма сил
Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма,
построенного на этих силах.
R Р1 Р 2
Р1
Р2
Р1
R
R
Р12 Р12 2 Р1 Р2 cos )
Р2
5. Аксиома равенства действия и противодействия
Всякому действию соответствует равное и противоположно направленное противодействие (III закон Ньютона).
Р12
Р 21
Р12 Р 21
6. Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердении
Равновесие сил, приложенных к деформирующемуся телу, сохраняется при его затвердении
3

9.

Тема 1
Связи и их реакции
Свободное твердое тело – это твердое тело, на перемещение которого не наложено никаких ограничений.
Связь – тело, ограничивающее свободу движения данного твердого тела.
Несвободное тело – это твердое тело, свобода движения которого ограничена связями.
Задаваемые (активные) силы выражают действие на твердое тело других тел, вызывающих или
способных вызвать изменение его кинематического состояния.
Реакция связи – это сила или система сил, выражающая механическое действие связи на тело.
Принцип освобождаемости твердых тел от связи (аксиома связи) – несвободное тело можно
рассматривать как свободное, на которое кроме задаваемых сил действуют реакции связей.
3

10.

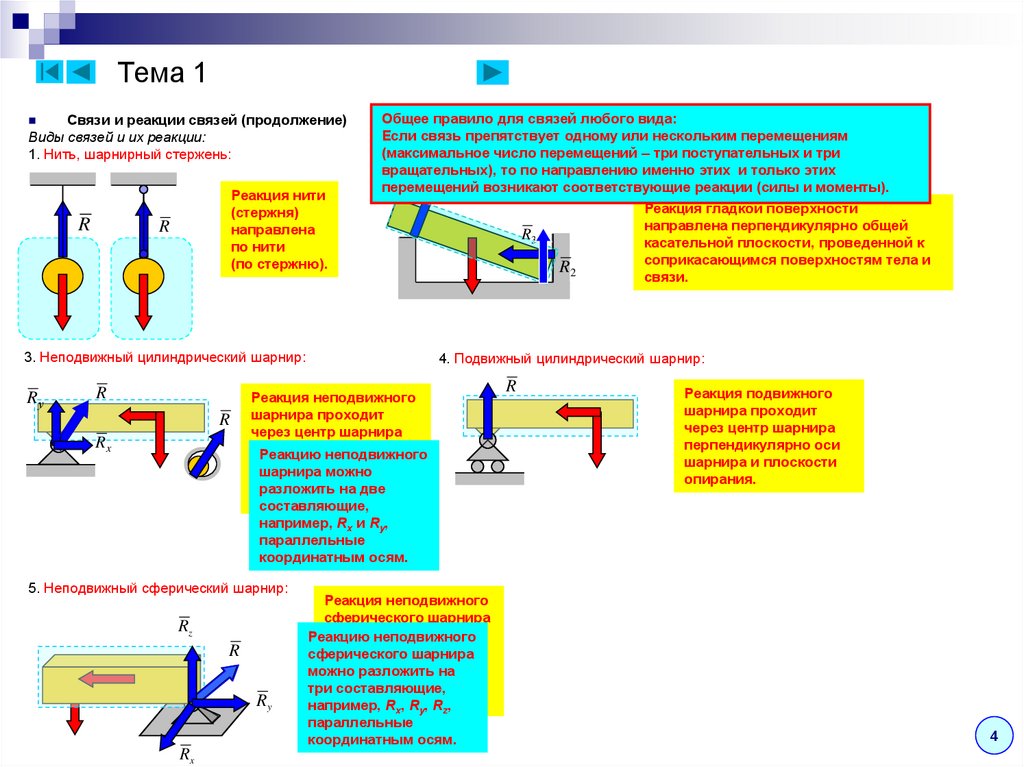
Тема 1
Связи и реакции связей (продолжение)
Виды связей и их реакции:
1. Нить, шарнирный стержень:
R
Реакция нити
(стержня)
направлена
по нити
(по стержню).
R
Общее правило для связей любого вида:
Если связь препятствует одному или нескольким перемещениям
число
перемещений – три поступательных и три
2.(максимальное
Абсолютно гладкая
поверхность:
вращательных), то по направлению именно этих и только этих
перемещений
возникают соответствующие реакции (силы и моменты).
R
3. Неподвижный цилиндрический шарнир:
Rу
R
R
Rx
1
R3
R2
Реакция гладкой поверхности
направлена перпендикулярно общей
касательной плоскости, проведенной к
соприкасающимся поверхностям тела и
связи.
4. Подвижный цилиндрический шарнир:
Реакция неподвижного
шарнира проходит
через центр шарнира
перпендикулярно
оси
Реакцию неподвижного
шарнира
и
имеет
шарнира можно
произвольное
разложить на две
направление.
составляющие,
R
Реакция подвижного
шарнира проходит
через центр шарнира
перпендикулярно оси
шарнира и плоскости
опирания.
например, Rx и Ry,
параллельные
координатным осям.
5. Неподвижный сферический шарнир:
Rz
R
Ry
Rx
Реакция неподвижного
сферического шарнира
проходит
через центр
Реакцию
неподвижного
шарнира и имеет
сферического
шарнира
произвольное
можно
разложить на
направление
в
три
составляющие,
пространстве.
например,
Rx, Ry, Rz,
параллельные
координатным осям.
4

11.

Тема 2
Р1
Р2
Система сходящихся сил – линии действия сил пересекаются в одной точке.
План исследования любой системы сил соответствует последовательному решению
трех вопросов :
1.
Как упростить систему?
2.
Каков простейший вид системы?
3.
Каковы условия равновесия системы?
R1, 2
R1, 2,3
R1, 2,3, 4
1.
Перенесем все силы по линии их действия в точку пересечения (кинематическое состояние
тела при этом не изменится – следствие из аксиомы присоединения).
Р3
Сложим первые две силы Р1 и Р2 (аксиома параллелограмма).
Количество сил уменьшилось на единицу.
R1, 2 Р1 Р 2
Сложим полученную равнодействующую R12 со следующей силой Р3.
Количество сил вновь уменьшилось на единицу.
R1, 2,3 R1, 2 Р 2
Повторим эту же операцию со следующей силой Р4.
Осталась всего одна сила, эквивалентная исходной системе сил.
R1, 2,3, 4 R1, 2,3 Р 4
Р4
Сложение сил построением параллелограммов можно заменить построением силового треугольника – выбирается одна из сил или изображается
параллельно самой себе с началом в любой произвольной точке, все другие силы изображаются параллельными самим себе с началом,
совпадающим с концом предыдущей силы.
Результатом такого сложения является вектор, направленный из начала первой силы к концу последней из сил.
2.
3.
Простейший вид системы – сила, приложенная в точке пересечения исходных сил. Таким
образом, сходящаяся система сил приводится к одной силе – равнодействующей (силе,
эквивалентной исходной системе сил), равной геометрической сумме сил системы.
R Р1 Р 2 Р3 Р 4 ... Р i
Если равнодействующая системы оказывается не равной нулю, тело под действием такой системы силы будет двигаться
в направлении равнодействующей (система сил не уравновешена). Для того, чтобы уравновесить систему достаточно
приложить силу, равную полученной равнодействующей и направленной в противоположную сторону (аксиома о двух
силах). Таким образом, условием равновесия системы сходящихся сил является обращение равнодействующей в
ноль.
R Рi 0
Это условие эквивалентно замкнутости силового треугольника определенным образом, а именно,
направление всех сил при обходе по контуру не изменяется по направлению:
5

12.

Тема 2
Р1
Теорема о равновесии трех непараллельных сил: линии действия трех непараллельных взаимно
уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке.
Р1
Р3
1.
Перенесем две силы по линии их действия в точку их пересечения (кинематическое состояние
тела при этом не изменится – следствие из аксиомы присоединения).
R12
2.
Сложим эти силы (аксиома параллелограмма). Теперь система состоит всего из двух сил. А такая
система находится в равновесии, если эти силы равны между собой и направлены по одной линии
в противоположные стороны. Таким образом, все три силы пересекаются в одной точке.
Р2
Р2
Теорема о трех силах может эффективно применяться для определения направления одной из двух реакций тел:
Реакция подвижного шарнира RB направлена вертикально (перпендикулярно
опорной плоскости). Направление (угол наклона к горизонту) реакции
неподвижного шарнира RA пока не определено.
Р
D
RA
Р
C
RB
Если тело под действием трех сил Р, RA и RB находится в равновесии,
то все три силы должны пересекаться в одной точке ( в точке С) :
A
Действительные направления и величины реакций легко определяются
построением силового треугольника и использованием подобия треугольников:
Аналитическое определение равнодействующей сходящихся сил –
Каждая из сил, геометрическая сумма которых дает равнодействующую, может быть
представлена через ее проекции на координатные оси и единичные векторы (орты):
h RB
RA
B
RA Р 2 RB2
l
z
Тогда равнодействующая выражается через проекции сил в виде:
Рi X i i Yi j Zi k
R ( X 1 X 2 ...)i (Y1 Y2 ...) j (Z1 Z 2 ...)k Rx i R y j Rz k
R y Yi ;
Rz Z i ;
Модуль
равнодействующей :
R
Направляющие
косинусы
равнодействующей:
Rx2 R y2 Rz2
Rx
;
R
Ry
cos( R , j )
.
R
R
cos( R , k ) z
R
cos( R , i )
Рi
Р i , xz
Xi
Группировка по ортам дает выражения для проекций равнодействующей:
Rx X i ;
Р i , yz
Zi
R Рi Р1 Р 2 .... X 1i Y1 j Z1k X 2i Y2 j Z 2 k ...
Отсюда
проекции
равнодействующей :
RB h
Р
l
x
k
i
Yi
j
y
Р i , xy
Уравнения равновесия сходящейся системы сил
Условие равновесия:
X i 0;
Равнодействующая
Отсюда
должна обращаться в ноль:
уравнения
Yi 0;
R 0
равновесия :
Z i 0.
6

13. Тема 3

Плоская произвольная система сил – силы лежат в одной плоскости и их линии действия не пересекаются в одной точке.
Для рассмотрения такой системы сил необходимо ввести новые понятия:
1.
Момент силы относительно точки на плоскости.
2.
Пара сил. Момент пары сил.
F
Момент силы относительно точки на плоскости – алгебраическая величина, равная
произведению модуля силы на плечо, взятая со знаком + (плюс), если вращение плоскости
под действием силы происходит против часовой стрелки,
и со знаком – (минус) в противном случае.
Плечо силы – длина перпендикуляра, опущенного из точки на линию действия силы.
h
Пара сил – совокупность двух параллельных друг другу сил, равных по величине и направленных
в противоположные стороны. Пара сил более не может быть упрощена (не может быть заменена одной
силой) и представляет собой новую силовую характеристику механического взаимодействия.
Момент пары сил на плоскости (теорема о моменте пары сил) – не зависит от выбора центра
приведения (полюса) и равен произведению модуля любой из сил пары на плечо пары, взятым со
знаком + (плюс), если вращение плоскости под действием пары сил происходит против часовой
стрелки, и со знаком – (минус) в противном случае.
Плечо пары сил – длина перпендикуляра, опущенного из любой точки на линии действия одной из
сил пары на линию действия другой силы этой пары.
В независимости момента пары от выбора полюса можно убедиться вычислением суммы моментов
от каждой из сил относительно любого центра.
M A ( F , F ) F (a b) F a Fb Fd
F F
F
b
d
a
A
F
M A ( F , F ) F h
Теоремы о парах: (Теоремы приводятся без доказательств. Подробные доказательства с графической анимацией см.
демонстрационную программу автора по теории пар “Теория пар” на сайте МИИТа. Посмотреть… )
О переносе пары сил в плоскости ее действия – Пару сил можно перенести в любое место в плоскости ее действия.
Кинематическое состояние тела не изменится.
Об эквивалентности пар сил – Пару сил можно заменить другой парой сил, если их моменты алгебраически равны. Кинематическое
состояние тела не изменится.
M ( F1 , F1 ) F1d1 , M ( F2 , F2 ) F2 d 2 ;
M A (F ) F h
A
F1d1 F2 d 2 ( F1 , F1 ) ( F2 , F2 )
О сложении пар сил на плоскости – Систему пар сил на плоскости можно заменить одной парой, момент которой равен
алгебраической сумме моментов исходных пар. Кинематическое состояние тела не изменится.
Условие равновесия системы пар сил M Mi 0
7

14. Тема 3 (продолжение – 3.2)

Приведение силы к заданному центру (метод Пуансо) – силу можно перенести параллельно самой себе в любую точку плоскости,
если добавить соответствующую пару сил, момент которой равен моменту этой силы относительно рассматриваемой точки.
Добавим к системе в точке A две силы, равные по величине между собой и величине заданной силы,
направленные по одной прямой в противоположные стороны и параллельные заданной силе:
F
M ( F , F )
F
F F F
d
Кинематическое состояние не изменилось (аксиома о присоединении).
Исходная сила и одна из добавленных сил противоположно направленная образуют пару сил.
Момент этой пары численно равен моменту исходной силы относительно центра приведения.
F
A
M ( F , F ) F d F h M A ( F )
Во многих случаях пару сил удобно изображать дуговой стрелкой.
Приведение плоской произвольной системы сил к заданному центру – выбираем произвольную точку на плоскости и каждую из сил
переносим по методу Пуансо в эту точку. Вместо исходной произвольной системы получим сходящуюся систему сил и систему пар.
F2
F1
F3
F2
F1
h1
h2
F3
h3
F1
F
A
A
R * Fi
- главный вектор,
M M A M iA
- главный момент.
Условием равновесия плоской произвольной системы сил является одновременное обращение главного вектора и главного
момента системы в ноль:
*
R Fi 0
MO
R*
2
F3
Сходящаяся система сил приводится к одной силе, приложенной в центре приведения, которая ранее
В общем
случае плоская
система
называлась равнодействующей, но теперь эта сила
не заменяет
исходнуюпроизвольная
систему сил, поскольку
сил
приводится
к
одной
силе,
называемой
после приведения возникла система пар. Система пар приводится к одной паре (теорема о сложении
главным
вектором
и к паре
с моментом, центра
равным
пар), момент которой равен алгебраической сумме
моментов
исходных
сил относительно
главному
моменту
всех
сил
системы
приведения.
относительно центра приведения:
M M A M iA 0
Уравнения равновесия (I форма) получаются в виде системы трех уравнений из условий равновесия с использованием выражений для
проекций главного вектора:
Существуют еще две формы уравнений
M iC 0; C
X i 0;
X i 0; x
Равновесия (II и III формы):
Yi 0;
M iA 0
M iB 0;
M iA 0 AB
M iB 0;
M iA 0 AB
8

15. Тема 3 (продолжение – 3.3)

Следует обратить внимание на то, что II и III формы уравнений равновесия имеют ограничения,
связанные с выбором одной из осей, например, x, и точки С относительно положения точек A и B.
Ограничения, накладываемые на выбор оси x (не перпендикулярно AB) и точки C (не лежит на AB),
гарантируют, что ни одно из уравнений не обращается в тождество, при выполнении двух других уравнений.
M iC 0; C
M iB 0;
M iA 0 AB
X i 0; x
M iB 0;
M iA 0 AB
Теорема Вариньона о моменте равнодействующей – Если система сил имеет равнодействующую, то момент этой
равнодействующей относительно любого центра равен алгебраической сумме моментов сил системы относительно того же центра.
Доказательство: Пусть система сил F1, F2, F3 … приводится к равнодействующей,
приложенной в точке O.
F3
F2
Такая система не находится в равновесии (R ≠ 0). Уравновесим эту систему силой R’, равной
равнодействующей R, направленной по линии ее действия в противоположную сторону
(аксиома о двух силах).
R
O
R
Таким образом, система исходных сил F1, F2, F3 … и уравновешивающей силы R’ находится
в равновесии и должна удовлетворять уравнениям равновесия, например:
M iA M A (R ) 0
R R
A
Поскольку сила R’, равна равнодействующей R и направлена по линии ее действия
в противоположную сторону, то MA(R’) = - MA(R). Подстановка этого равенства в уравнение
равновесия дает:
M iA M A (R) 0 или M A ( R) M iA
F1
Примеры использования теоремы о моменте равнодействующей:
1. Определение момента силы относительно точки, когда сложно вычислять плечо силы. Например:
F2
F
F1
b
a
A
Силу F разложим на составляющие F1 и F2. Тогда момент силы F относительно точки A
можно вычислить как сумму моментов каждой из сил относительно этой точки:
M A ( F ) F1b F2 a ( F cos )b ( F sin )a
2. Доказательство необходимости ограничений для II и III форм уравнений равновесия:
Если
M 0 , то система приводится к равнодействующей, при этом она проходит через
h
Если при этом
iA
точку A, т.к. ее момент относительное этой точки должен быть равен нулю (теорема Вариньона).
M iB 0
x
, то равнодействующая должна также проходить через точку B.
Тогда проекция равнодействующей на ось, перпендикулярную AB, и момент равнодействующей относительно
точки, лежащей на AB, будут тождественно равны нулю при любом значении равнодействующей.
R
A
С
B
9