Similar presentations:
Благоприятствующие элементарные события. Вероятности событий
1.
Благоприятствующиеэлементарные события.
Вероятности событий
2.
Перейдём к наиболее сложным случайным событиям.Предположим при броске кубика событие «на кубике
нечётное число» или «на кубике более трёх очков».
Для обозначения случайных событий используют
заглавные буквы A, B, C, D и так далее.
Всякое событие состоит из элементарных событий.
Пример:
Событие «на кубике нечётное число» при броске
игральной кости состоит из трёх элементарных
событий: «на кубике единица», «на кубике тройка», «на
кубике пятёрка».
Элементарные события, благодаря которым исполняется
событие А, называются событиями,
благоприятствующими событию А.
3.
В случайном опыте наступает толькоодно из элементарных событий.
Но если элементарное
событие благоприятствует двум различным
событиям А и В, то
события А и В могут произойти одновременно.
4.
ПРИМЕР:Костя, Паша и Серёжа (К, П и С) встают в ряд. Все
события в этом опыте, которые возможны,
складываются из элементарных событий, которых в этом
случае всего шесть:
КПС
КСП
ПКС
ПСК
СКП
СПК
Рассмотрим событие «Серёжа будет первым». Оно
наступает, когда случилось одно из двух элементарных
событий СКП и СПК. То есть представленные
элементарные события благоприятствуют событию
«Серёжа стоит первым».
Вместо словесного описания события можно записать
событие «Серёжа будет первым» (назовём его событием А)
перечнем благоприятствующих элементарных событий в
фигурных скобках: А={СКП;СПК}.
5.
Вероятности, как мы уже отмечали ранее,принято означать буквой P. Это от латинского слова
«probabilitas», что в переводе — «вероятность».
Вероятность события есть сумма вероятностей
элементарных событий, благоприятствующих этому
событию.
Интерпретируем это правило в формулу.
Пусть событию В содействуют элементарные
события a, b, c: В={a,b,c}.
Тогда вероятность события В есть сумма
вероятностей этих событий:
P(B)=P(а)+P(b)+P(c).
6.
Число слагаемых в правой частиравенства может быть каким угодно и
даже бесконечным.
Вероятности всех элементарных событий
неотрицательны и в сумме равны 1.
7.
Следовательно, вероятность события В также неотрицательна и не превосходит 1:
0≤P(В)≤1.
В частных случаях вероятность невозможного
события равна 0, в то время как вероятность
достоверного события равна 1.
ПРИМЕР:
В игре в домино вероятность выигрыша некоторого
игрока N равна 0,02, а вероятность ничьей равна 0,2.
Необходимо найти вероятность события С «игрок N не
проиграл».
Этому событию благоприятствуют элементарные
события «игрок N выиграл» и «игрок N сыграл вничью».
Таким образом, P(C)= 0,02+0,2 = 0,22.
8.
Задание 1Бросают одну игральную кость. Выбери
элементарные события, которые
благоприятствуют событию A — «выпало чётное
число очков»:
9.
Задание 2В случайном опыте — четыре элементарных
события a, b, c, d, вероятности которых
соответственно равны 0,03; 0,03; 0,27 и 0,22. Найди
вероятность события, которому благоприятствуют
элементарные события а, b и d.
10.
Задание 3Игральную кость бросают дважды. Сколько
элементарных событий благоприятствуют событию —
«при втором броске выпало больше очков, чем при
первом»?
11.
Задание 4Игральную кость бросают дважды. Сколько
элементарных событий благоприятствуют событию —
«произведение очков равно 12»?
12.
Задание 5В шахматной партии Антон играет с Игорем.
Вероятность выигрыша Антона равна 0,26,
вероятность ничьей составляет 0,19.
Найди вероятность того, что Игорь не
проиграет.
13.
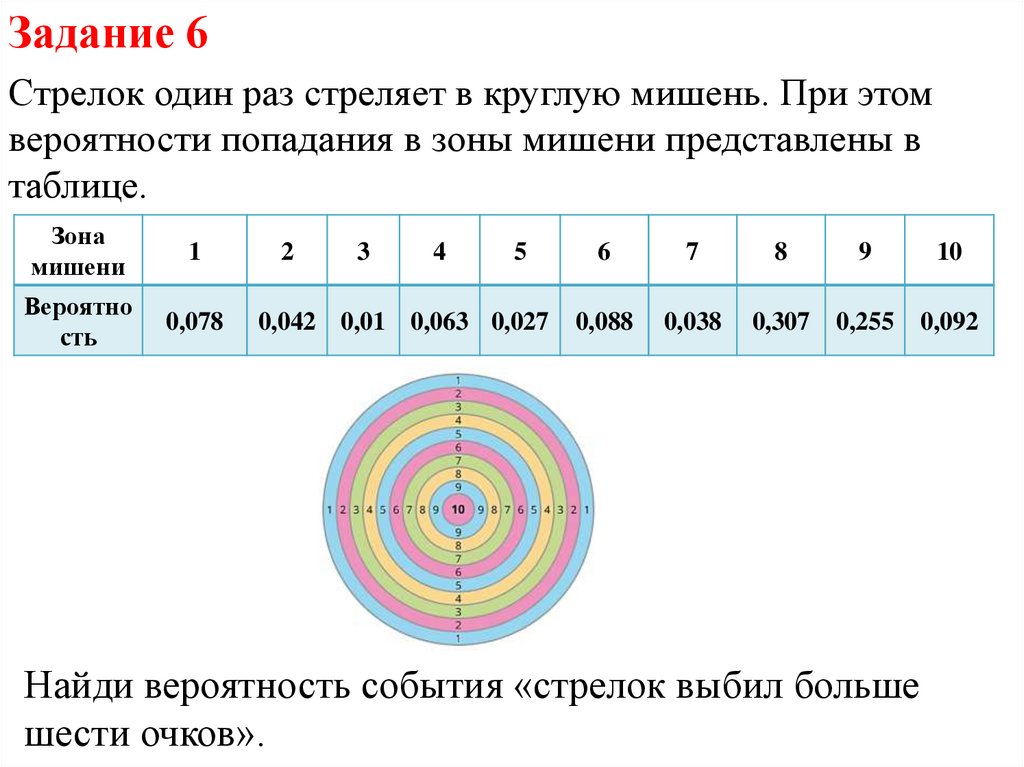
Задание 6Стрелок один раз стреляет в круглую мишень. При этом
вероятности попадания в зоны мишени представлены в
таблице.
Зона
мишени
1
Вероятно
сть
0,078
2
3
4
5
0,042 0,01 0,063 0,027
6
7
8
9
10
0,088
0,038
0,307
0,255
0,092
Найди вероятность события «стрелок выбил больше
шести очков».
14.
Задание 615.
Задание 7В классе количество учеников равно 4.
Среди них есть ученик по имени Илья.
Учитель в течение урока по очереди вызывает к
доске двух человек.
Сколько элементарных событий
благоприятствуют событию «К доске
вышел Илья»?
16.
Задание 8Пётр Петрович отправился на рыбалку и оценивает
свои перспективы следующим образом:
•один шанс из четырёх за то, что он поймает
только леща;
•один к десяти за то, что ему попадётся только карп;
•один к пятидесяти за то, что выловит и леща,
и карпа.
Найди вероятность того, что не видать рыбаку:
1) ни одного леща.
2) ни одного карпа.
3) ни леща, ни карпа.
17.
Задание 9Вероятность того, что новая ручка пишет
плохо (или не пишет), равна 0,26.
Покупатель в магазине выбирает одну такую
ручку.
Найди вероятность того, что эта ручка пишет
хорошо.
18.
Задание 10Вероятность того, что новая ручка пишет
плохо (или не пишет), равна 0,47.
Покупатель в магазине выбирает одну такую
ручку.
Найди вероятность того, что эта ручка пишет
хорошо.
19.
Задание 11Автомобиль подъезжает к перекрёстку.
Вероятность элементарного события «автомобиль
свернёт вправо» равна 0,4, вероятность
элементарного события «автомобиль свернёт
влево» равна 0,1, вероятность элементарного
события «автомобиль поедет прямо» равна 0,16.
Найди вероятность события A «автомобиль не
поедет обратно».
20.
Задание 12В некотором опыте возможно три
элементарных события a, b и c.
Вероятность того, что наступит либо b,
либо c, равна 0,66.
Найди вероятность элементарного
события a.
21.
Задание 13В некотором опыте возможно три элементарных
события a, b и c.
Вероятность того, что наступит либо событие a,
либо событие b, равна 0,38.
Вероятность того, что наступит либо событие a,
либо событие c, равна 0,77.
Найди вероятность каждого из элементарных
событий.
P(a)
?
P(b)
?
P(c)
?
22.
Домашнее заданиеЗадание № 1
Бросают одну игральную кость.
Выбери элементарные события, которые
благоприятствуют событию A — «выпало
нёчетное число очков»:
23.
Домашнее заданиеЗадание № 2
В случайном опыте — четыре элементарных
события a, b, c, d, вероятности которых
соответственно равны 0,06; 0,05; 0,01 и 0,19.
Найди вероятность события, которому
благоприятствуют элементарные события b и c.
24.
Домашнее заданиеЗадание № 3
Игральную кость бросают дважды.
Сколько элементарных событий благоприятствуют
событию — «выпали одинаковые числа»?
25.
Домашнее заданиеЗадание № 4
В шахматной партии Павел играет
с Борисом. Вероятность
выигрыша Павла равна 0,14, вероятность
ничьей составляет 0,2.
Найди вероятность того, что никто не
выиграет.
26.
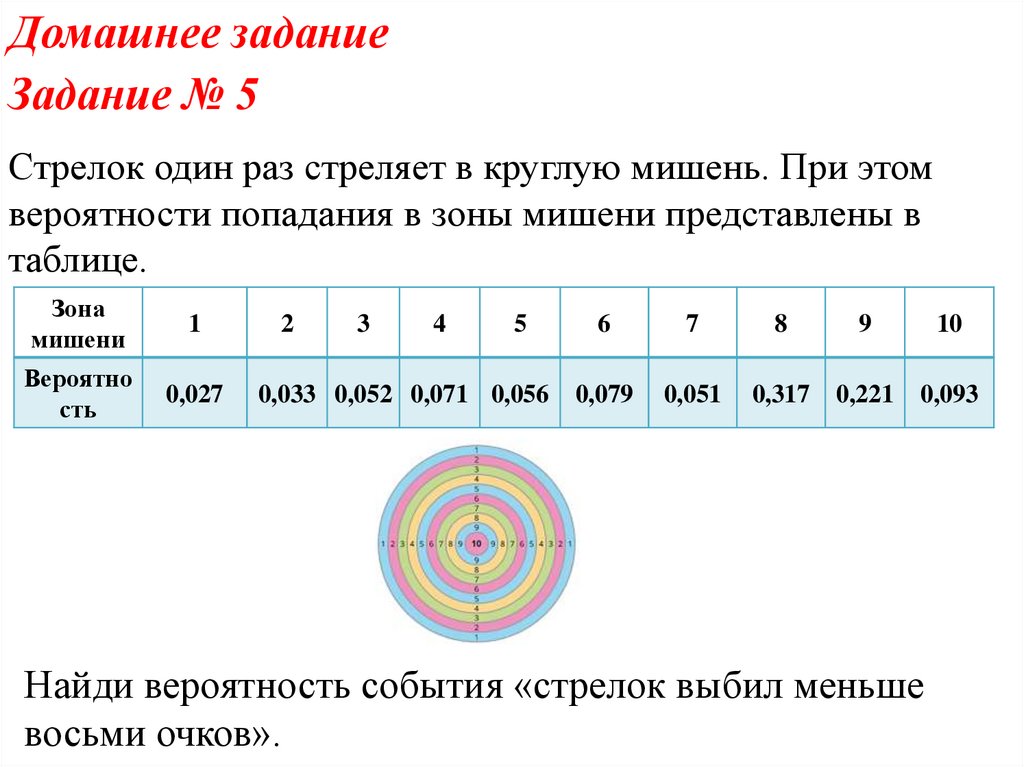
Домашнее заданиеЗадание № 5
Стрелок один раз стреляет в круглую мишень. При этом
вероятности попадания в зоны мишени представлены в
таблице.
Зона
мишени
1
Вероятно
сть
0,027
2
3
4
5
0,033 0,052 0,071 0,056
6
7
8
9
10
0,079
0,051
0,317
0,221
0,093
Найди вероятность события «стрелок выбил меньше
восьми очков».
27.
Домашнее заданиеЗадание № 5
28.
Домашнее заданиеЗадание № 6
В классе количество учеников равно 7.
Среди них есть ученик по имени Илья.
Учитель в течение урока по очереди вызывает к
доске двух человек.
Сколько элементарных событий
благоприятствуют событию «К доске
вышел Илья»?
























 mathematics
mathematics








