Similar presentations:
Свойства и графики тригонометрических функций
1. Свойства и графики тригонометрических функций
16.01.20252. Понятие функции
Если каждому значению x из некоторогомножества чисел поставлено в соответствие по
определенному правилу число y, то говорят, что
на этом множестве задана функция. При этом х
называют независимой переменной или
аргументом, а у – зависимой переменной или
функцией. Зависимость переменной у от
переменной х называют функциональной
зависимостью. Записывают y=f(x).
3. Область определения функции
Областью определения функции называютмножество всех допустимых значений
переменной x. Геометрически – это проекция
графика функции на ось Ох.
4. Множество значений функции
Множество значений функции — множествовсех значений, которые функция принимает на
области определения. Геометрически – это
проекция графика функции на ось Оy.
5. Тригонометрические функции Синус и косинус
Свойство 1. Для любого числа t справедливы равенства:sin (-t) = - sin t;
cos (-t) = cos t.
Свойство 2. Для любого числа t справедливы равенства:
sin (t + 2πk) = sin t,
cos (t + 2πk) = cos t.
Свойство 3. Для любого числа t справедливы равенства:
sin (t + π) = - sin t;
cos (t + π) = - cos t.
6. Содержание
• Свойства функции y = sin x и ее график• Свойства функции y = cos x и ее график
• Свойства функции y = tg x и ее график
• Свойства функции y = ctg x и ее график
7. Свойства функции y = sin x и ее график.
Составим таблицу значений, для построенияграфика функции y = sin x
x
y
2
6
0
-1
1
2
0
0
6
2
1
1
2
0
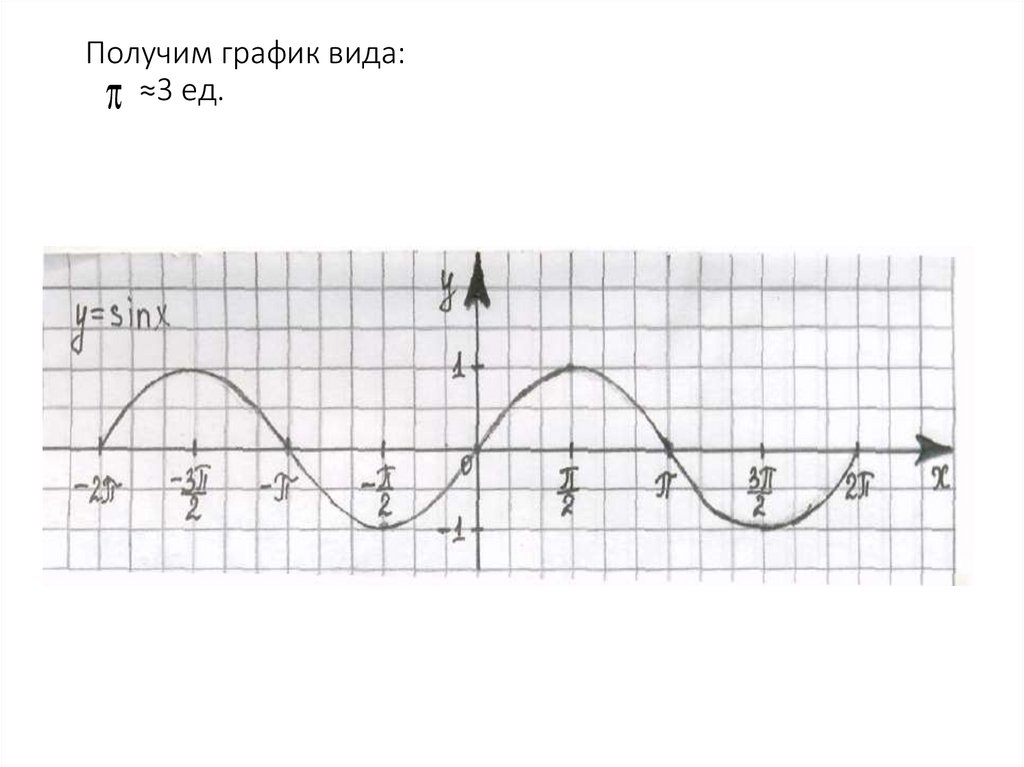
8. Получим график вида: ≈3 ед.
9. Свойства функции y = sin x
10. Тригонометрические функции Функция y = sin x Свойства функции y = sin x. Функция y = sin x Свойства функции y = sin x.
Функция y = sin xСвойства функции y = sin x.
Свойство 1. D(y) = (-∞;+∞).
Свойство 2. y = sin x – нечетная функция.
Свойство 3. Функция y = sin x убывает на отрезке [-π/2+2πk; π/2 + 2πk] и возрастает на
отрезке [π/2 + 2πk; 3π/2 + 2πk ], где k є Z.
Свойство 4. Функция ограничена и сверху и снизу (-1 ≤ sin t ≤ 1).
Свойство 5. yнаим = -1; yнаиб = 1.
Свойство 6. Функция y = sin x периодическая, ее основной период равен 2π.
Свойство 7. y = sin x – непрерывная функция.
Свойство 8. E(y) = [-1;1].
Свойство 9. Функция выпукла вверх на отрезке [0 + 2πk; π + 2πk],
выпукла вниз на отрезке [π + 2πk; 2π + 2πk], где k є Z.
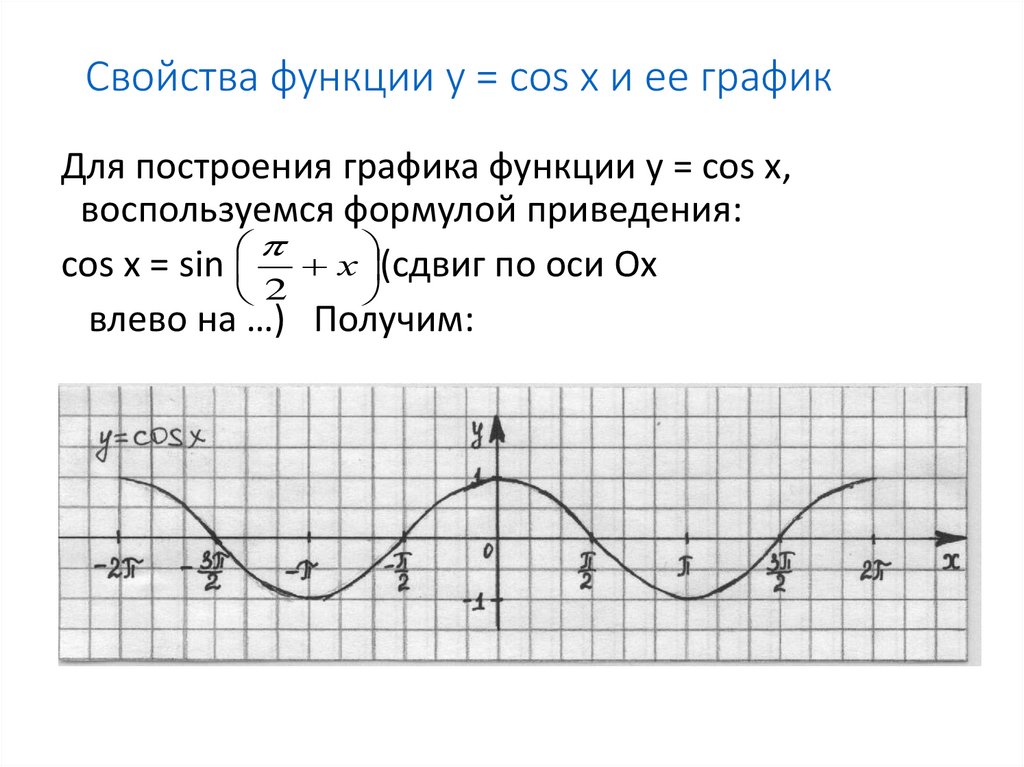
11. Свойства функции y = cos x и ее график
Для построения графика функции y = cos x,воспользуемся формулой приведения:
cos x = sin х (сдвиг по оси Ох
2
влево на …) Получим:
12. Свойства функции y = cos x
13. Тригонометрические функции Функция y = cos x Свойства функции y = cos x. Функция y = cos x Свойства функции y = cos x.
Функция y = cos xСвойства функции y = cos x.
Свойство 1. D(y) = (-∞;+∞).
Свойство 2. y = cos x – четная функция.
Свойство 3. Функция y = cos x убывает на отрезке [2πk; π + 2πk] и возрастает на
отрезке [π + 2πk; 2π + 2πk ], где k є Z.
Свойство 4. Функция ограничена и сверху и снизу (-1 ≤ cos t ≤ 1).
Свойство 5. yнаим = -1; yнаиб = 1.
Свойство 6. Функция y = cos x периодическая, ее основной период равен 2π.
Свойство 7. y = cos x – непрерывная функция.
Свойство 8. E(y) = [-1; 1].
Свойство 9. Функция выпукла вверх на отрезке [-0,5π+2πk; 0,5π+2πk],
выпукла вниз на отрезке [0,5π+2πk; 1,5π+2πk], где k є Z.
14.
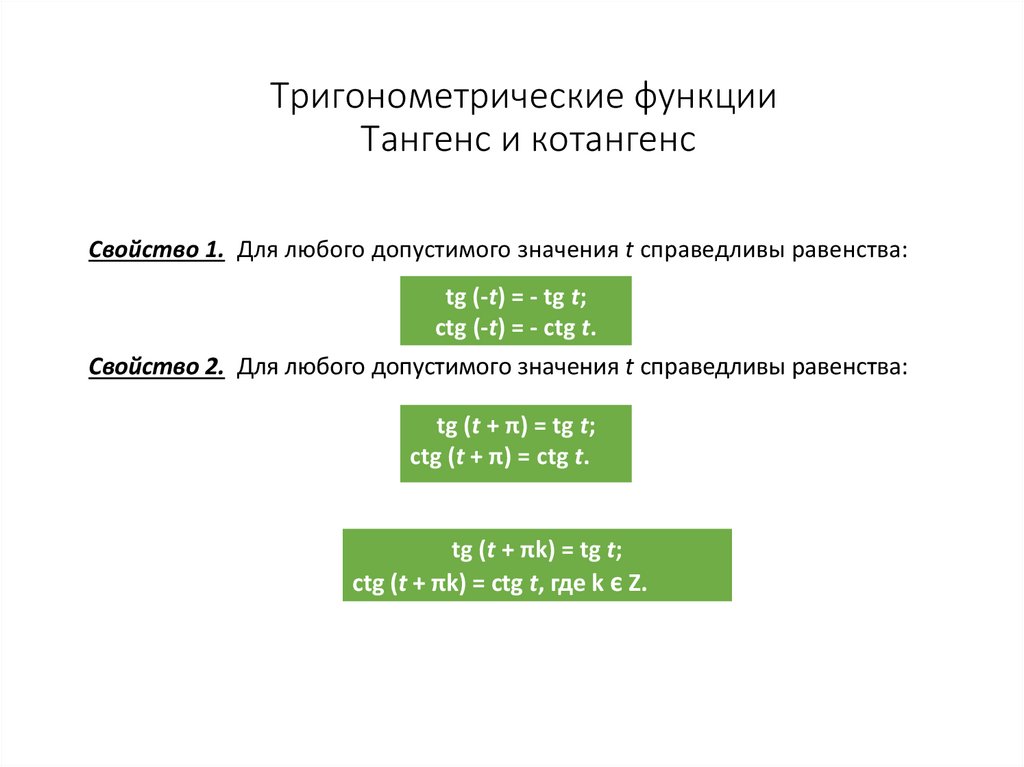
Тригонометрические функцииТангенс и котангенс
Свойство 1. Для любого допустимого значения t справедливы равенства:
tg (-t) = - tg t;
ctg (-t) = - ctg t.
Свойство 2. Для любого допустимого значения t справедливы равенства:
tg (t + π) = tg t;
ctg (t + π) = ctg t.
tg (t + πk) = tg t;
ctg (t + πk) = ctg t, где k є Z.
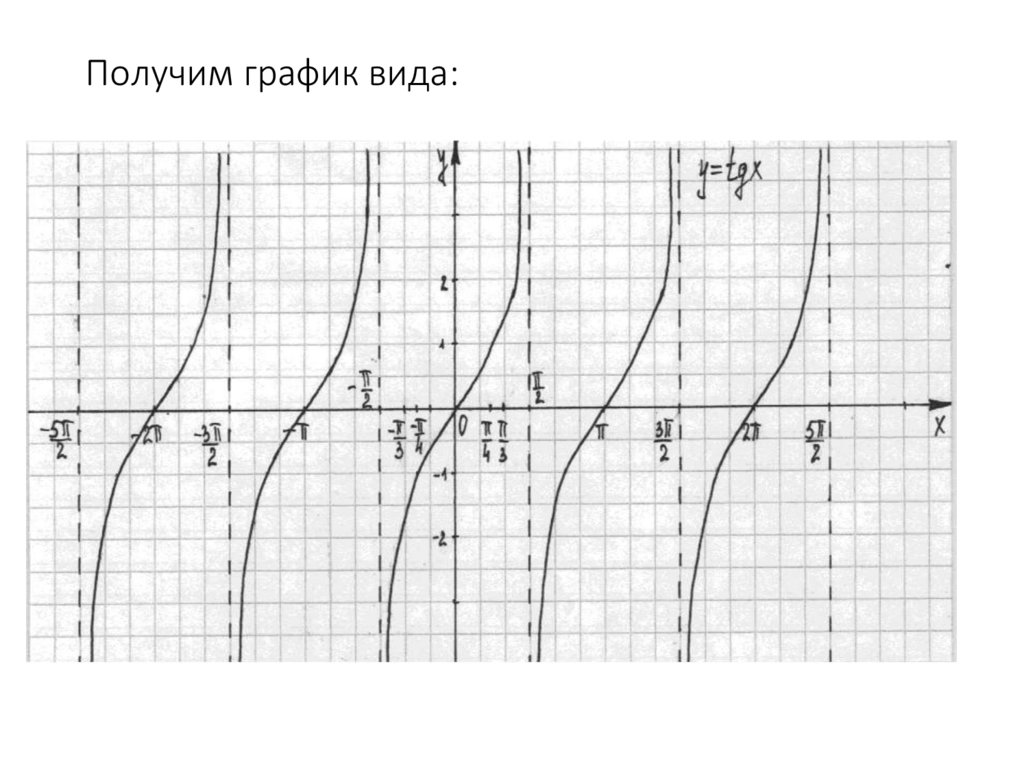
15. Свойства функции y = tg x и ее график
Составим таблицу значений, для построенияграфика функции y = tg x
16. Получим график вида:
17. Свойства функции y = tg x
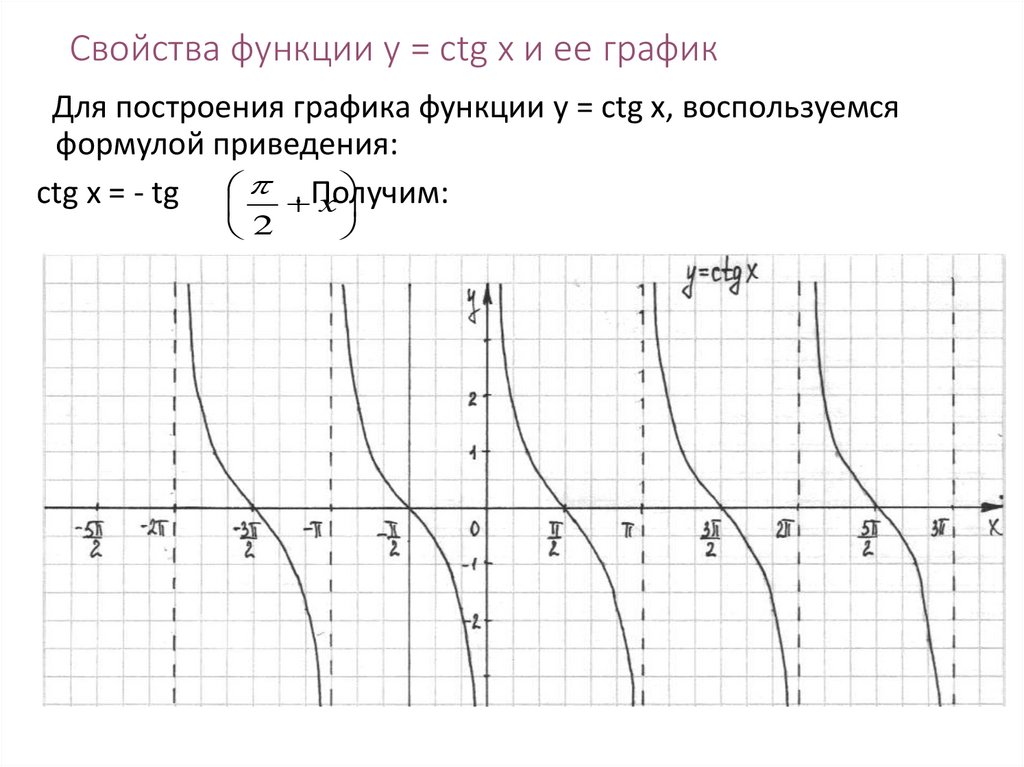
18. Свойства функции y = ctg x и ее график
Для построения графика функции y = ctg x, воспользуемсяформулой приведения:
ctg x = - tg . Получим:
х
2














 mathematics
mathematics








