Математическое моделирование. Форма и принципы представления математических моделей

1.

МАТЕМАТИЧЕСКОЕ
МОДЕЛИРОВАНИЕ
ЛЕКЦИЯ 1. ВВЕДЕНИЕ В ДИСЦИПЛИНУ
«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ»

2.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
• Моделирование - это замещение некоторого объекта
А другим объектом Б.
Замещаемый объект А называется оригиналом или
объектом моделирования, а замещающий Б - моделью.
• Цель
моделирования
получение,
обработка,
представление и использование информации об
объектах, которые взаимодействуют между собой и
внешней средой.

3.

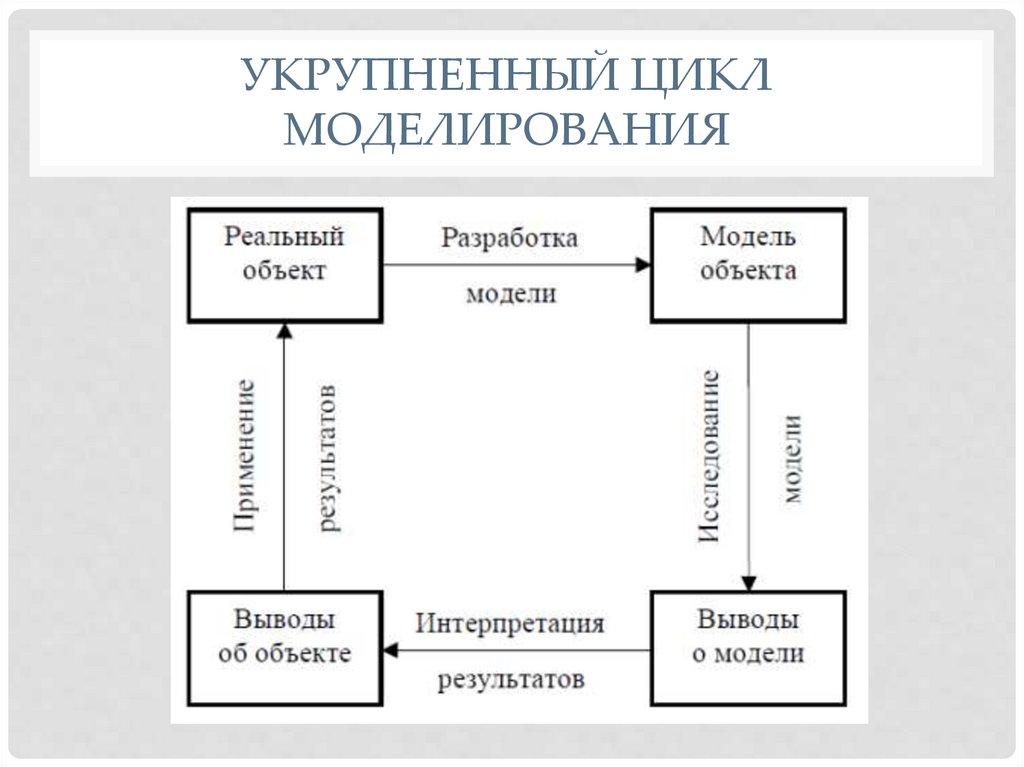
УКРУПНЕННЫЙ ЦИКЛ
МОДЕЛИРОВАНИЯ

4.

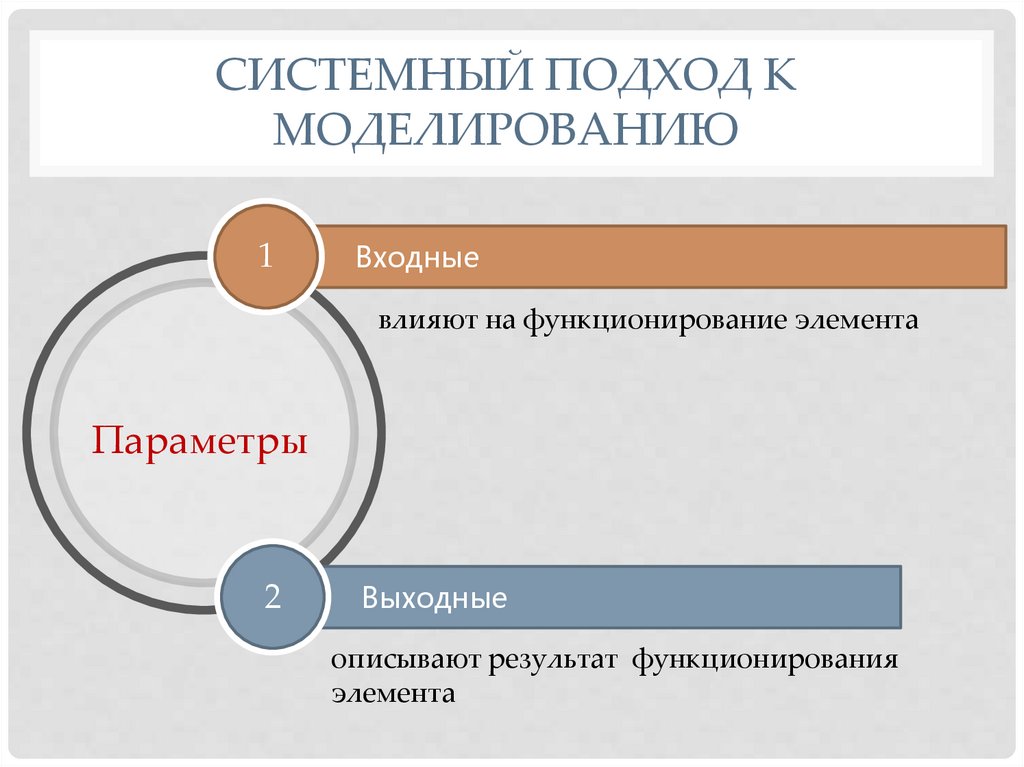
СИСТЕМНЫЙ ПОДХОД К
МОДЕЛИРОВАНИЮ
Системой называется совокупность взаимодействующих
элементов, объединенных наличием общей цели.
Подсистемой называется часть системы, имеющая
собственную (локальную) цель, согласованную с целью
системы.
Элементом называется неделимая часть системы.
Дерево целей называется схема, отражающая иерархию
целей.

5.

СИСТЕМНЫЙ ПОДХОД К
МОДЕЛИРОВАНИЮ
Сущность системного подхода к
моделированию заключается в единстве
процессов декомпозиции и
композиции.

6.

СИСТЕМНЫЙ ПОДХОД К
МОДЕЛИРОВАНИЮ
Декомпозицией называется метод, основанный на
использовании структуры системы и позволяющий
заменить решение одной большой задачи решением
нескольких более простых задач.
Подходы:
Структурный заключается в разбиении системы на
подсистемы и элементы;
Функциональный предполагает построение модели
каждого элемента на основе анализа его поведения без
использования информации о структуре.

7.

СИСТЕМНЫЙ ПОДХОД К
МОДЕЛИРОВАНИЮ
Композицией
называется
моделирование
связей
подсистем и элементов между собой и с внешней средой.
Связь
между
элементами
осуществляется
через
множество параметров, которые для одних элементов
являются входными, а для других – выходными.

8.

СИСТЕМНЫЙ ПОДХОД К
МОДЕЛИРОВАНИЮ
1
Входные
влияют на функционирование элемента
Параметры
2
Выходные
описывают результат функционирования
элемента

9.

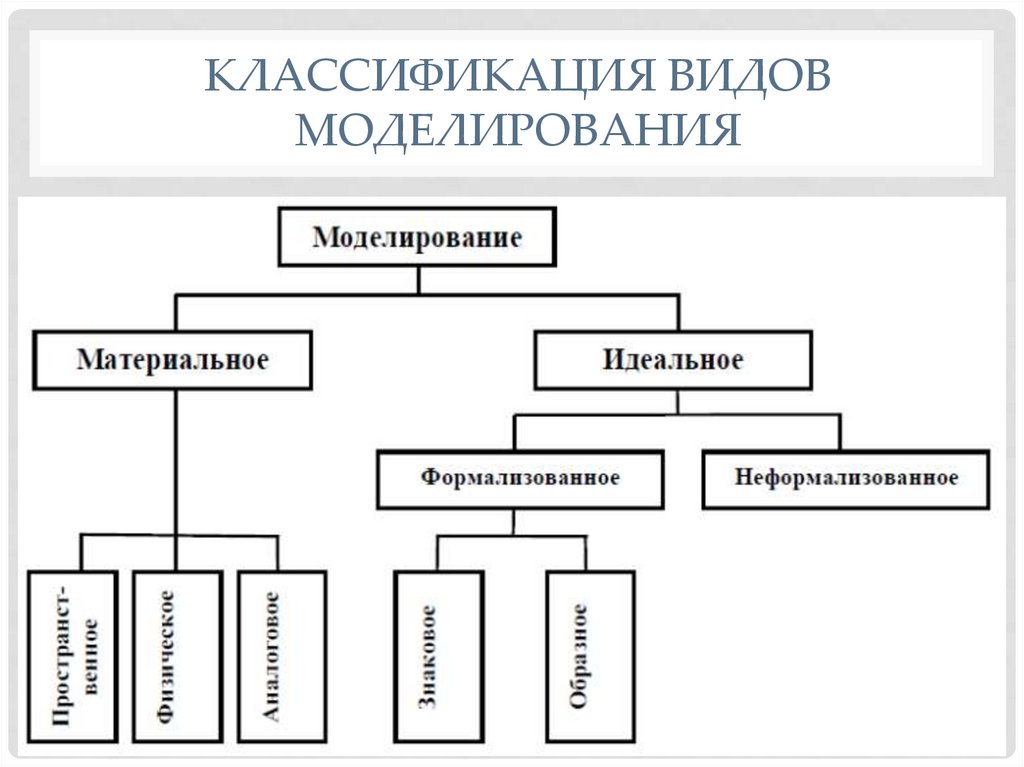
КЛАССИФИКАЦИЯ ВИДОВ
МОДЕЛИРОВАНИЯ

10.

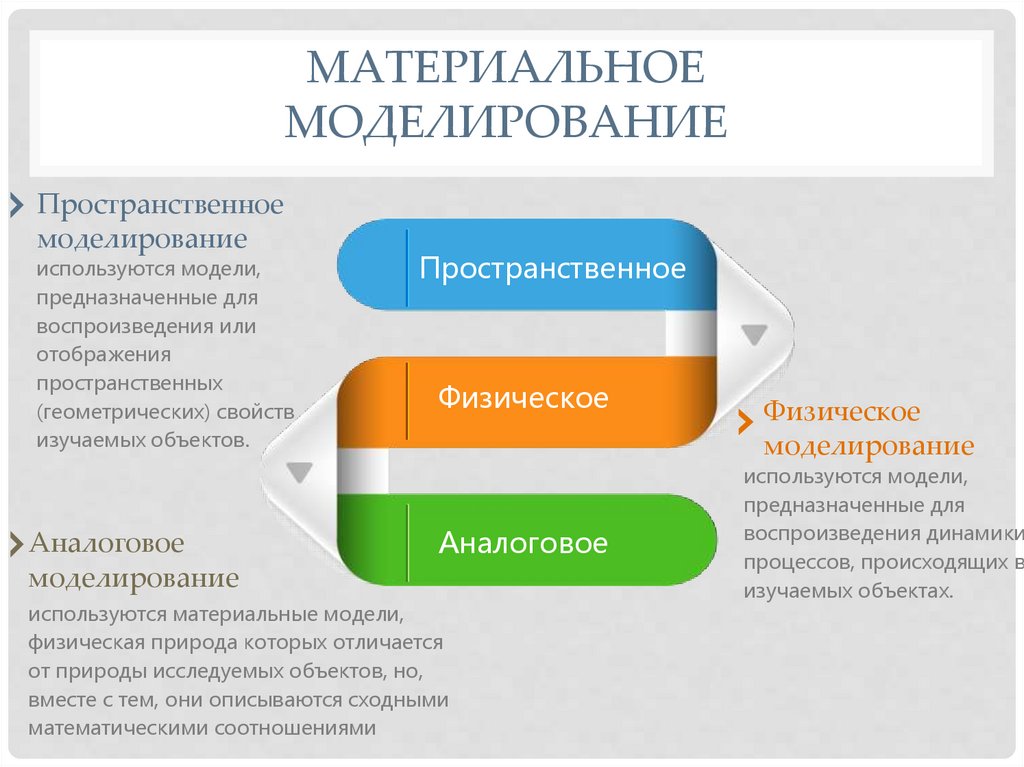
МАТЕРИАЛЬНОЕ
МОДЕЛИРОВАНИЕ
Пространственное
моделирование
используются модели,
предназначенные для
воспроизведения или
отображения
пространственных
(геометрических) свойств
изучаемых объектов.
Аналоговое
моделирование
Пространственное
Физическое
Аналоговое
используются материальные модели,
физическая природа которых отличается
от природы исследуемых объектов, но,
вместе с тем, они описываются сходными
математическими соотношениями
Физическое
моделирование
используются модели,
предназначенные для
воспроизведения динамики
процессов, происходящих в
изучаемых объектах.

11.

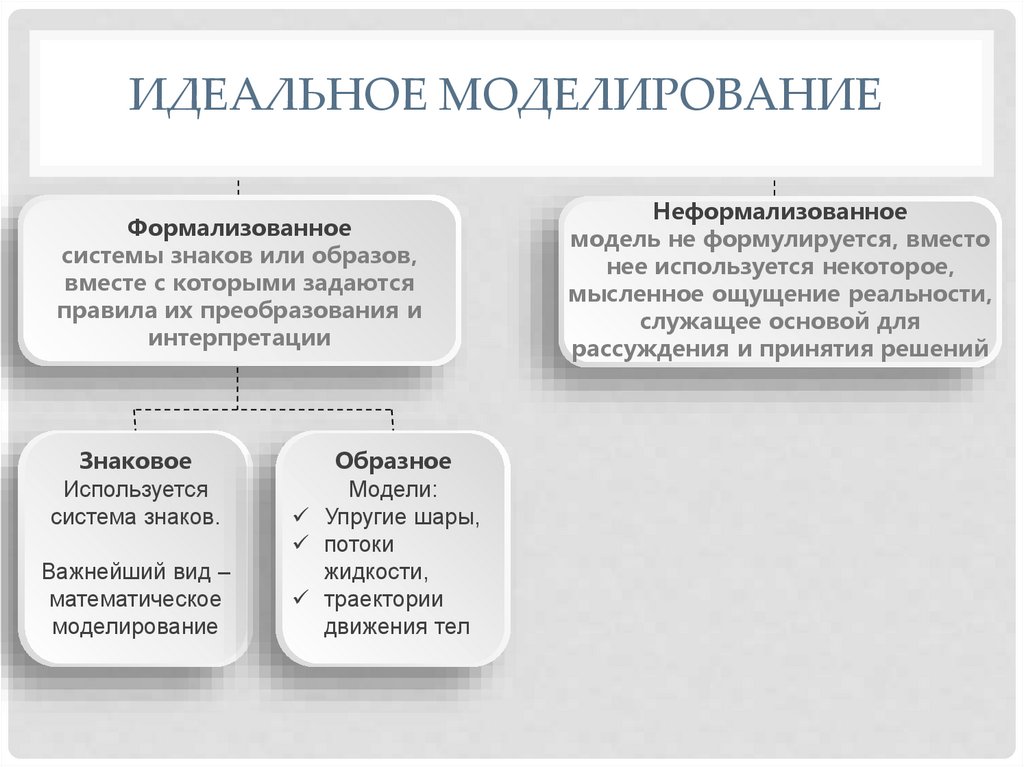
ИДЕАЛЬНОЕ МОДЕЛИРОВАНИЕ
Формализованное
системы знаков или образов,
вместе с которыми задаются
правила их преобразования и
интерпретации
Знаковое
Используется
система знаков.
Важнейший вид –
математическое
моделирование
Образное
Модели:
Упругие шары,
потоки
жидкости,
траектории
движения тел
Неформализованное
модель не формулируется, вместо
нее используется некоторое,
мысленное ощущение реальности,
служащее основой для
рассуждения и принятия решений

12.

КЛАССИФИКАЦИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Математические модели представляют собой
описание объектов в виде математических символов,
формул, выражений.
1. По способу построения модели:
Аналитические – строятся на основе информации, содержащейся в известных
законах природы.
Статистические – строятся на основании обработки экспериментальных
данных.
Комбинированные – сочетают достоинства аналитических и статистических
моделей.

13.

КЛАССИФИКАЦИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
2. Одномерные и многомерные. Различают по количеству входных
переменных, входящих в модель.
3. Линейные и нелинейные. Для линейных моделей справедлив принцип
суперпозиции, согласно которому реакция объекта на суммарное воздействие
равна сумме реакций объекта на элементарные воздействия:
4. Статические и динамические. В динамических моделях переменные
зависят от времени, в статических – нет.
5. Стационарные и нестационарные. Стационарные модели описывают
процессы, инвариантные относительно времени начала процесса.
Нестационарные модели описывают процессы, течение которых зависит от
времени их начала.

14.

КЛАССИФИКАЦИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
6. Модели с параметрами, сосредоточенными или распределенными в
пространстве. В моделях с распределенными параметрами переменные
зависят от пространственных координат, в моделях с сосредоточенными
параметрами – не зависят.
7. Модели, дискретные и непрерывные (во времени). В дискретных моделях
время принимает фиксированные значения, в непрерывных – любые значения.
8. Детерминированные и стохастические (вероятностные) модели.
Детерминированные модели являются воспроизводимыми: при одинаковых
условиях модель всегда дает один и тот же результат.
В стохастических моделях некоторые параметры являются случайными
величинами, и результаты моделирования при каждой реализации
отличаются друг от друга.

15.

СВОЙСТВА МАТЕМАТИЧЕСКИХ
МОДЕЛЕЙ И ТРЕБОВАНИЯ К НИМ
1. Целенаправленность. Должны фигурировать параметры, описывающие
цель объекта, а так же параметры, с помощью управления которыми
можно добиться достижения цели.
2. Точность. Определяется величинами погрешности, с которыми
рассчитываются выходные параметры.
3. Непротиворечивость. Характеризует отсутствие абсурдных ответов и
выводов при использовании модели.
4. Реалистичность. Оценивается путем также расчета типовых примеров,
для которых заранее известен результат (точный или ориентировочный).
5. Устойчивость. Называется слабая чувствительность к погрешностям ее
параметров.

16.

СВОЙСТВА МАТЕМАТИЧЕСКИХ
МОДЕЛЕЙ И ТРЕБОВАНИЯ К НИМ
6. Удобство использования. Является одним из основных свойств
математических моделей, что обусловлено самим методом
моделирования.
7. Универсальность. Обеспечивает описание с помощью нее как можно
более широкий класс объектов.
8. Адаптивность и возможность изменения. Модели, обладающие этими
свойствами можно корректировать при изменении окружающих условий
и совершенствовать для улучшения ее свойств.

17.

СВОЙСТВА МАТЕМАТИЧЕСКИХ
МОДЕЛЕЙ И ТРЕБОВАНИЯ К НИМ
9. Экономичность, простота, физический смысл.
экономичность модели - минимизация затрат на ее разработку и
реализацию.
физический смысл - изучение модели с целью избежания возможных
ошибок.
принцип простоты - из нескольких моделей с одинаковыми другими
свойствами нужно выбрать наиболее простую.
9. Адекватность математической модели является ее интегральным
свойствам, объединяющим другие наиболее важные свойства.

18.

МАТЕМАТИЧЕСКОЕ
МОДЕЛИРОВАНИЕ
ЛЕКЦИЯ 2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
И ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ

19.

ПРЕДМЕТ МАТЕМАТИЧЕСКОГО
МОДЕЛИРОВАНИЯ
Математическая модель – это приближенное описание какоголибо класса явлений или объектов реального мира на языке
математики
Цель – исследовать объекты и предсказать результаты будущих
наблюдений

20.

особенности
механических
систем и
процессов
01
факторы,
характеризуются,
измеримые величины
как
02
основа – уравнения, описывающие
фундаментальные законы природы
03
трудность при разработке – описание
недостоверно
известных
характеристик объекта
04
современные требования к моделям
приводят к необходимости учета
множества факторов

21.

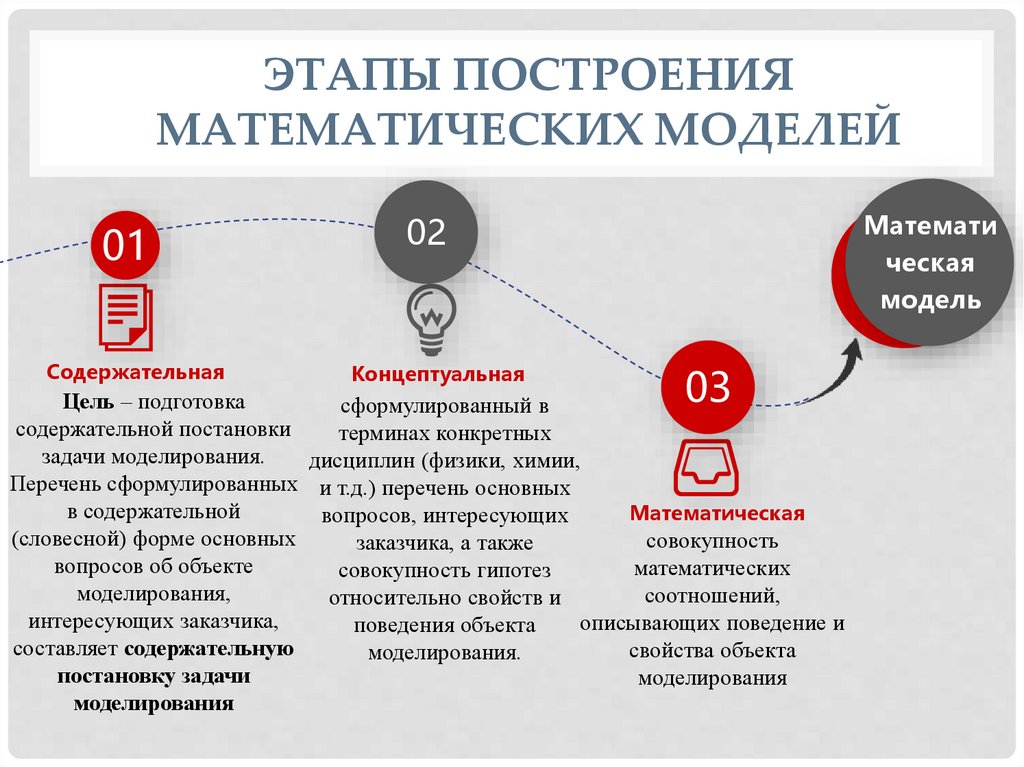
ЭТАПЫ ПОСТРОЕНИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
01
02
Содержательная
Концептуальная
Математи
ческая
модель
03
Цель – подготовка
сформулированный в
содержательной постановки
терминах конкретных
задачи моделирования.
дисциплин (физики, химии,
Перечень сформулированных и т.д.) перечень основных
в содержательной
Математическая
вопросов, интересующих
(словесной) форме основных
совокупность
заказчика, а также
вопросов об объекте
математических
совокупность гипотез
моделирования,
соотношений,
относительно свойств и
интересующих заказчика,
описывающих поведение и
поведения объекта
составляет содержательную
свойства объекта
моделирования.
постановку задачи
моделирования
моделирования

22.

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
ОБЪЕКТА
Виды взаимосвязей параметров объекта
1) вектор-функций
2) неявные функции
3) обыкновенные дифференциальные
уравнения
4) дифференциальные уравнения с
частными производными

23.

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
ОБЪЕКТА
Виды взаимосвязей параметров объекта
5) интегро-дифференциальные уравнения
6) оптимизационная задача
7) вычислительный алгоритм
8) вероятностное (стохастическое) описание
Под математическим описанием понимается полная совокупность данных,
функций и методов вычисления, позволяющая получать результат!

24.

ПРОСТЕЙШАЯ КЛАССИФИКАЦИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
01
02
03
04
05
линейные или нелинейные
стационарные или нестационарные
непрерывные или дискретные
детерминированные или стохастические
четкие или нечеткие

25.

АЛГОРИТМ НАУЧНЫХ ИССЛЕДОВАНИЙ С
ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО
МОДЕЛИРОВАНИЯ
Феноменологическое (физическое)
описание оригинала
изучение оригинала
формулировка
выводов
исследования
анализ результатов
ВЭ, сравнение с
результатами
изучения оригинала
проведение ВЭ в
целях
исследования,
обработка его
результатов
1
2
10
9
8
7
3
математическое
описание оригинала
4
разработка
алгоритмического и
ПО для реализации
мат. описания с
помощью ЭВМ
5
проведение
контрольного
вычислительного
эксперимента (ВЭ)
6
оценка адекватности
результатов
контрольного ВЭ
реальному случаю
планирование ВЭ в целях
исследования

26.

ПОНЯТИЕ ВЫЧИСЛИТЕЛЬНОГО
ЭКСПЕРИМЕНТА
Вычислительный эксперимент (ВЭ) – это эксперимент
над математической моделью объекта на ЭВМ, который
состоит в том, что по одним параметрам модели
вычисляются другие её параметры и на этой основе
делаются выводы о свойствах явления, описываемого
математической моделью.
Под адекватностью математической модели будет
пониматься
степень
соответствия
результатов,
полученных
по
разработанной
модели,
данным
эксперимента или тестовой задачи.

27.

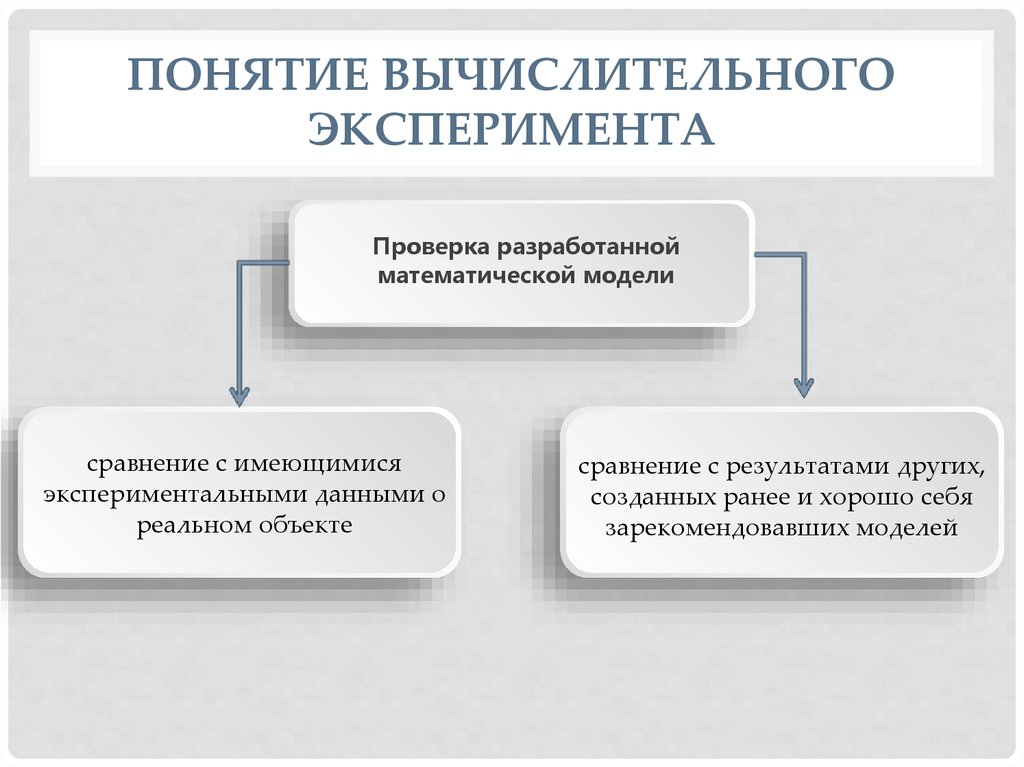
ПОНЯТИЕ ВЫЧИСЛИТЕЛЬНОГО
ЭКСПЕРИМЕНТА
Проверка разработанной
математической модели
сравнение с имеющимися
экспериментальными данными о
реальном объекте
сравнение с результатами других,
созданных ранее и хорошо себя
зарекомендовавших моделей

28.

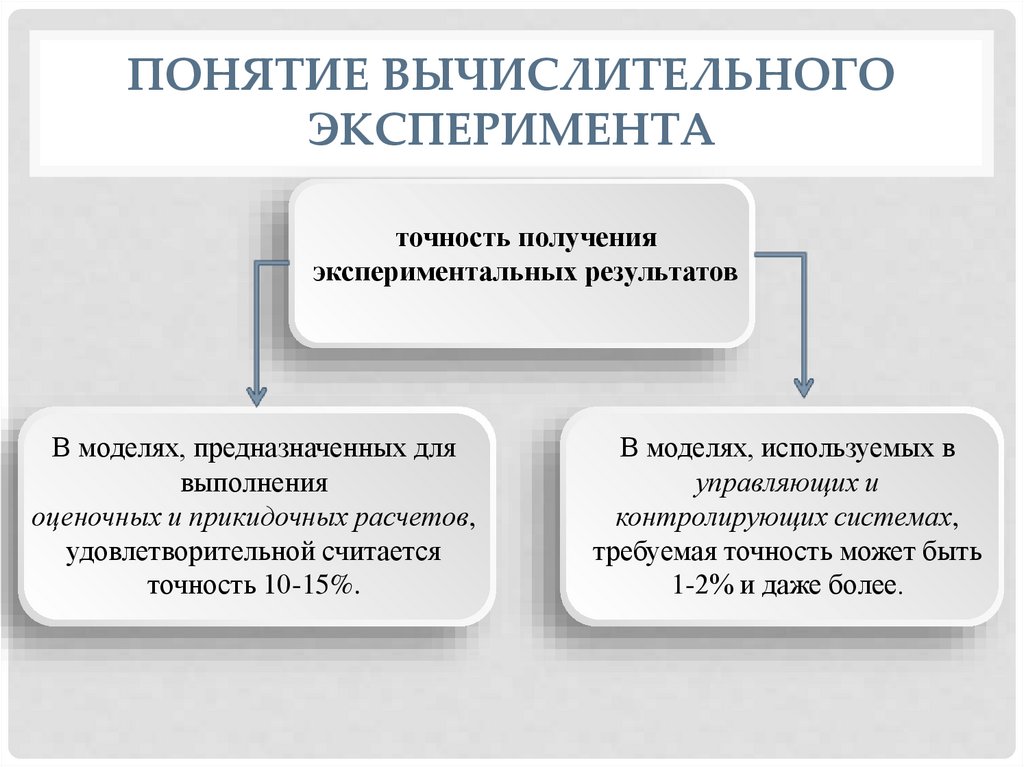
ПОНЯТИЕ ВЫЧИСЛИТЕЛЬНОГО
ЭКСПЕРИМЕНТА
точность получения
экспериментальных результатов
В моделях, предназначенных для
выполнения
оценочных и прикидочных расчетов,
удовлетворительной считается
точность 10-15%.
В моделях, используемых в
управляющих и
контролирующих системах,
требуемая точность может быть
1-2% и даже более.

29.

МАТЕМАТИЧЕСКОЕ
МОДЕЛИРОВАНИЕ
ЛЕКЦИЯ 3. РЕШЕНИЕ ОДНОКРИТЕРИАЛЬНЫХ
ЗАДАЧ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ

30.

ПРОЦЕСС ПРИНЯТИЯ РЕШЕНИЯ МОЖНО ПРЕДСТАВИТЬ КАК
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ СЛЕДУЮЩИХ
ДЕЙСТВИЙ
01
02
03
04
Анализ ситуации и формализация исходной проблемы
На этом этапе необходимо четко сформулировать
проблему, понять и сформулировать цели, которые
хочется достичь в виде решения проблемы.
Построение математической модели
перевод формальной модели, построенной на
предыдущем этапе, на язык математических
отношений
Анализ математической модели и получение
математического решения проблемы
анализируется построенная математическая модель,
проверяется адекватность модели и находится
решение математической задачи, вытекающей из этой
модели
Анализ математического решения проблемы и
формирование управленческого решения
выполняется анализ чувствительности, и затем на
основе этого математического решения
формируется управленческое решение

31.

ПОСЛЕ ВЫПОЛНЕНИЯ ЭТИХ ЭТАПОВ
СЛЕДУЕТ ЭТАП РЕАЛИЗАЦИИ ПРИНЯТОГО
РЕШЕНИЯ
сформулировать проблему
1
сформулировать цели
2
указать, что считать решением проблемы
3
выявить и описать возможности
достижения целей
4
выявить и описать факторы, от которых
может зависеть решение проблемы
5
выявить и описать ограничения, препятствующие достижению
целей
6
описать возможные альтернативные способы решения проблемы
7

32.

ПРИМЕР 1
Предприятие выпускает четыре вида продукции и использует три
типа основного оборудования: токарное, фрезерное и шлифовальное.
Затраты времени на изготовление единицы продукции для каждого из
типов оборудования приведены в таблице. В ней же указаны общий фонд
рабочего времени каждого из типов оборудования, а также прибыль от
реализации одного изделия данного вида.

33.

ПРИМЕР 1
Необходимо:
a) Определить такой объем выпуска каждого из изделий, при котором
общая прибыль от их реализации является максимальной.
b) Что произойдет с общей прибылью, если прибыль от продажи
продукции вида 4 вырастет втрое?
c) Как изменится общая прибыль, если предприятию будет необходимо
выпускать не меньше 1 единиц продукции 3?
d) Если увеличить время использования фрезерных станков на 80
станко-часов, то можно ли будет уменьшить время использования
других станков?

34.

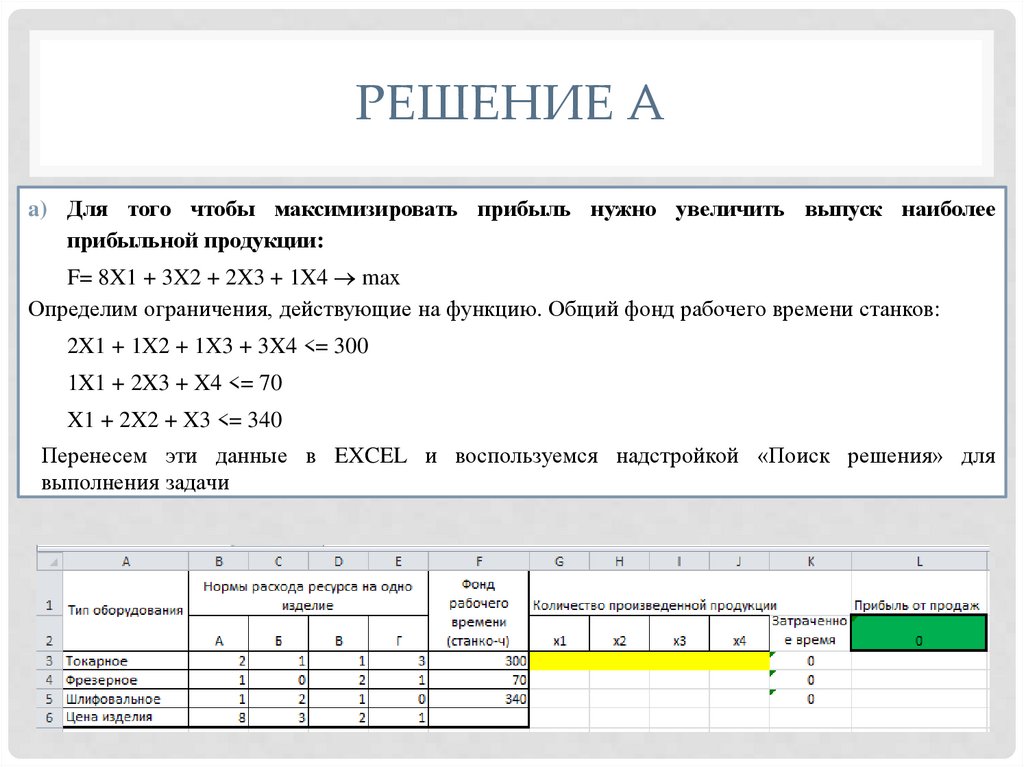
РЕШЕНИЕ А
a) Для того чтобы максимизировать прибыль нужно увеличить выпуск наиболее
прибыльной продукции:
F= 8X1 + 3X2 + 2X3 + 1X4 max
Определим ограничения, действующие на функцию. Общий фонд рабочего времени станков:
2X1 + 1X2 + 1X3 + 3X4 <= 300
1X1 + 2X3 + X4 <= 70
X1 + 2X2 + X3 <= 340
Перенесем эти данные в EXCEL и воспользуемся надстройкой «Поиск решения» для
выполнения задачи

35.

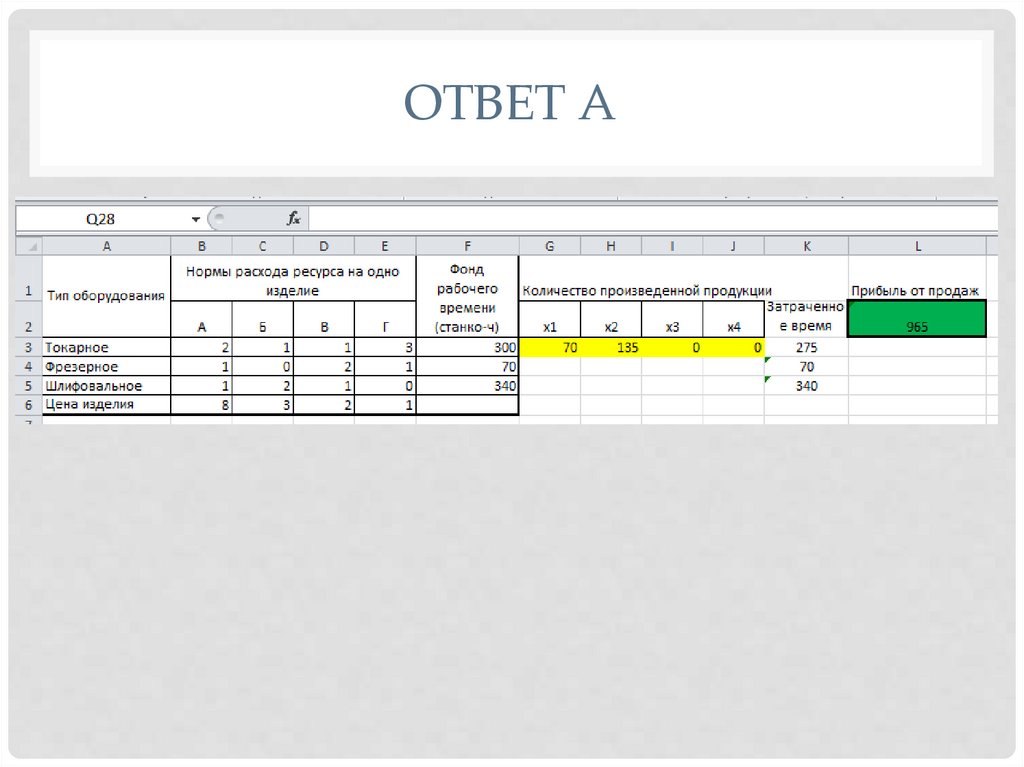
ОТВЕТ А

36.

РЕШЕНИЕ B
b) Что произойдет с общей прибылью, если прибыль от продажи продукции вида 4
вырастет втрое?
• Для решения этой задачи увеличим стоимость реализации 4 продукции до 3.
Тем не менее результат остался прежним.

37.

РЕШЕНИЕ C
c) Как изменится общая прибыль, если предприятию будет необходимо выпускать не
меньше 1 единиц продукции 3.
Для выполнения этого запроса внесем еще одно ограничение
В результате внесенных изменений прибыльность предприятия снизилась

38.

РЕШЕНИЕ D
d) Если увеличить время использования фрезерных станков на 80 станко-часов, то можно
ли будет уменьшить время использования других станков?
Увеличивая время использования фрезерных станков добились ощутимого
прироста прибыли предприятия и снижение использования шлифовальных
станков, загрузка токарных станков несущественно увеличилась.

39.

ОТВЕТ
Таким образом, можно сделать вывод о том, что в результате
проведенных исследований прибыльность предприятия можно
увеличить, максимизируя выпуск продукции 1 и 2 типа, а также
увеличив время использования фрезерных станков.

40.

МАТЕМАТИЧЕСКОЕ
МОДЕЛИРОВАНИЕ
ЛЕКЦИЯ 4. ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ. ПРИМЕРЫ ЗАДАЧ

41.

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.
ПОСТАНОВКА ЗАДАЧИ
Линейное программирование (ЛП 1951 г) - это направление
математического программирования, изучающее методы решения
экстремальных
задач,
которые
характеризуются
линейной
зависимостью между переменными и линейным критерием.
Джордж Данциг
Тьяллинг Купманс

42.

ФОРМУЛИРОВКА ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ (ЗЛП)
ЗАДАЧА О
ДИЕТЕ
составляется
наиболее
экономный рацион питания,
удовлетворяющий
определенным
медицинским требованиям.
В качестве переменных x1,
x2,…,
xn
выступают
количества
продуктов
питания, используемых в
рационе
ЗАДАЧА О СОСТАВЛЕНИИ
ПЛАНА ПРОИЗВОДСТВА
Класси
ческие
пример
ы
составляется
наиболее
выгодный
план
производства
продукции,
удовлетворяющий
определенным
ограничениям. В качестве
переменных x1, x2,…, xn
выступают
количества
продукции,
выпускаемых
предприятием

43.

РАССМОТРЕНИЕ ПРИМЕРА ЗАДАЧИ О
СОСТАВЛЕНИИ ПЛАНА ПРОИЗВОДСТВА
Пусть
некоторая
производственная
единица
(предприятие, цех, отдел и т.д.) может производить n
видов товаров G1, G2,…, Gn, используя при этом m видов
сырьевых ресурсов R1, R2,…,Rm, запасы которых
ограничены величинами b1, b2,…,bm.
Tехнологией производства товара Gj назовем набор чисел
aij, показывающий, какое количество i-го ресурса
необходимо для производства единицы товара Gj.

44.

РАССМОТРЕНИЕ ПРИМЕРА ЗАДАЧИ О
СОСТАВЛЕНИИ ПЛАНА ПРОИЗВОДСТВА
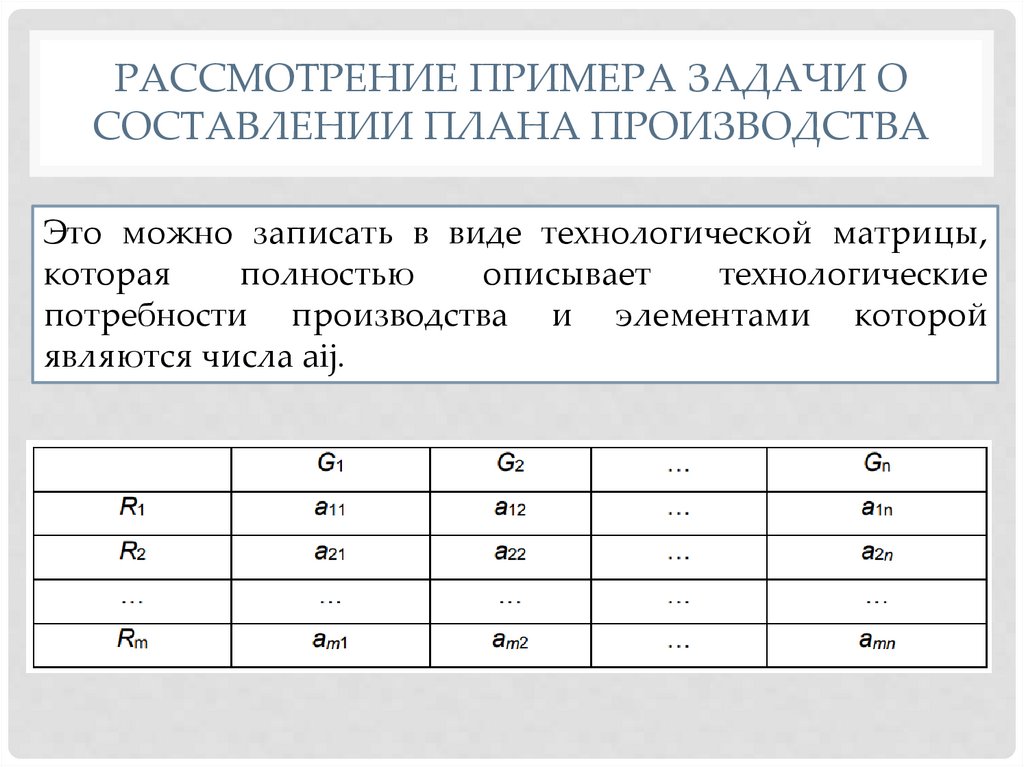
Это можно записать в виде технологической матрицы,
которая
полностью
описывает
технологические
потребности производства и элементами которой
являются числа aij.

45.

РАССМОТРЕНИЕ ПРИМЕРА ЗАДАЧИ О
СОСТАВЛЕНИИ ПЛАНА ПРОИЗВОДСТВА
Предположим также, что известны цены реализации
единицы каждого товара с1, с2, …, сn.
Обозначим через x1, x2,…, xn планируемое
производство единиц товаров G1, G2,…, Gn. В силу
имеющейся технологической матрицы для этого
потребуется:

46.

РАССМОТРЕНИЕ ПРИМЕРА ЗАДАЧИ О
СОСТАВЛЕНИИ ПЛАНА ПРОИЗВОДСТВА
С учетом ограничений на запасы ресурсов, а также
очевидных условий неотрицательности переменных x1,
x2,…, xn получим следующую систему линейных
неравенств:

47.

РАССМОТРЕНИЕ ПРИМЕРА ЗАДАЧИ О
СОСТАВЛЕНИИ ПЛАНА ПРОИЗВОДСТВА
Естественно
предположить,
что
целью
производственной
единицы
является
получение
максимальной выручки за произведенную продукцию,
т.е. максимизация функции:

48.

РАССМОТРЕНИЕ ПРИМЕРА ЗАДАЧИ О
СОСТАВЛЕНИИ ПЛАНА ПРОИЗВОДСТВА
Таким образом, с учетом естественного требования
неотрицательности переменных получаем линейную
оптимизационную
задачу,
которая
может
быть
представлена в следующей формальной записи:

49.

ФОРМЫ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
1) Общей задачей ЛП называется задача, которая
состоит в определении максимального (минимального)
значения функции

50.

ФОРМЫ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Решить задачу линейного программирования - это
значит, найти все ее оптимальные планы или доказать
их отсутствие.

51.

ФОРМЫ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
2) Особенностью стандартной задачи ЛП является то,
что ее ограничения представлены в виде линейных
неравенств, а также условий неотрицательности на
переменные, присутствующие в задаче:

52.

ФОРМЫ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
3) Ограничения основной задачи ЛП представляют
собой линейные ограничения-равенства, а также условия
неотрицательности на переменные:
Между различными формами задач линейного
программирования существует тесная взаимосвязь, в
смысле возможности перехода от одной формы записи к
другой.

53.

ПЕРЕХОД ОТ СТАНДАРТНОЙ ЗАДАЧИ К
ОСНОВНОЙ

54.

ВОЗМОЖНЫЕ СЛУЧАИ ДОПУСТИМОГО
МНОЖЕСТВА РЕШЕНИЙ ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
01
Допустимое множество
решений пусто
02
Допустимое множество выпуклый ограниченный
многогранник
03
Допустимое множество выпуклое неограниченное
многогранное множество

55.

ВОЗМОЖНЫЕ СЛУЧАИ ОПТИМАЛЬНЫХ РЕШЕНИЙ
(ПЛАНОВ) ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
01
Задача не имеет
оптимальных решений
02
Задача имеет единственное
решение (единственный
оптимальный план)
03
Задача имеет бесконечное
множество оптимальных
решений

56.

ПРАВИЛО ПРИВЕДЕНИЯ ЗЛП К
КАНОНИЧЕСКОМУ ВИДУ:
1) Если в исходной задаче некоторое ограничение
(например, первое) было неравенством, то оно
преобразуется в равенство, введением в левую часть
некоторой неотрицательной переменной, при чем в
неравенства
«≤»
вводится
дополнительная
неотрицательная переменная со знаком «+»; в случаи
неравенства «≥» - со знаком «-»
В каждое из неравенств вводится своя “уравнивающая” переменная,
после чего система ограничений становится системой уравнений.

57.

ПРАВИЛО ПРИВЕДЕНИЯ ЗЛП К
КАНОНИЧЕСКОМУ ВИДУ:
2) Если в исходной задаче некоторая переменная не
подчинена условию неотрицательности, то ее заменяют (в
целевой функции и во всех ограничениях) разностью
неотрицательных переменных
3) Если в ограничениях правая часть отрицательна, то
следует умножить это ограничение на (-1)

58.

ПРАВИЛО ПРИВЕДЕНИЯ ЗЛП К
КАНОНИЧЕСКОМУ ВИДУ:
4) Наконец, если исходная задача была задачей на
минимум, то введением новой целевой функции F1 = -F
преобразуем задачу на минимум функции F в задачу на
максимум функции F1.
Таким образом, всякую задачу линейного
программирования можно сформулировать в
канонической форме.

59.

ПРАВИЛО ПРИВЕДЕНИЯ ЗЛП К
СТАНДАРТНОЙ ФОРМЕ
Преобразование задачи на минимум в задачу на
обеспечение не отрицательности производится так же,
как и раньше. Всякое равенство в системе ограничений
равносильно
системе
взаимопротивоположных
неравенств:
Таким образом, всякую задачу линейного
программирования можно сформулировать в
стандартной форме.

60.

ПРИМЕР

61.

РЕШЕНИЕ

62.

РЕШЕНИЕ

63.

МАТЕМАТИЧЕСКОЕ
МОДЕЛИРОВАНИЕ
Л Е К Ц И Я 5 . О Б Щ И Й В И Д И О С Н О В Н А Я З А Д АЧ А
Л И Н Е Й Н О Г О П Р О Г РА М М И Р О В А Н И Я . С И М П Л Е К С – М Е Т О Д

64.

СУТЬ СИМПЛЕКСНОГО МЕТОДА
необходимо
максимизировать
(минимизировать)
некий
критерий (валовой доход от реализации продукции, совокупные
операционные расходы на производство товаров и т.д.) при наложенных
линейных ограничениях.
симплекс-метод
–
это
усовершенствованный
графический
метод
решения
задач
линейного
программирования в многомерном пространстве

65.

АЛГОРИТМ СИМПЛЕКС-МЕТОДА
Шаг 1
Привести
систему
ограничений к
базисной форме
01
03
Шаг 2
02
найти опорное
решение,
служащее
«точкой отсчета»
Шаг 3
последовательно перебирать вершины симплекса. Если в
данной точке значение критерия больше (меньше)
предыдущего, то процесс продолжается. Когда значение
критерия уже нельзя улучшить, значит, решение найдено

66.

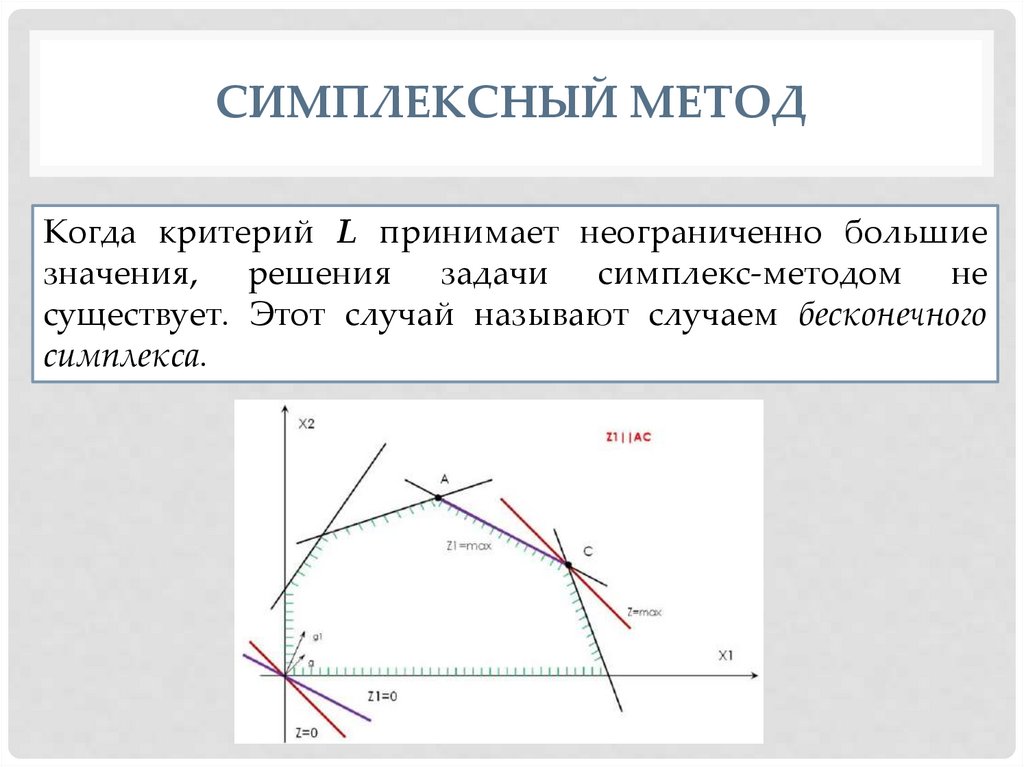
СИМПЛЕКСНЫЙ МЕТОД
Когда критерий L принимает неограниченно большие
значения, решения задачи симплекс-методом не
существует. Этот случай называют случаем бесконечного
симплекса.

67.

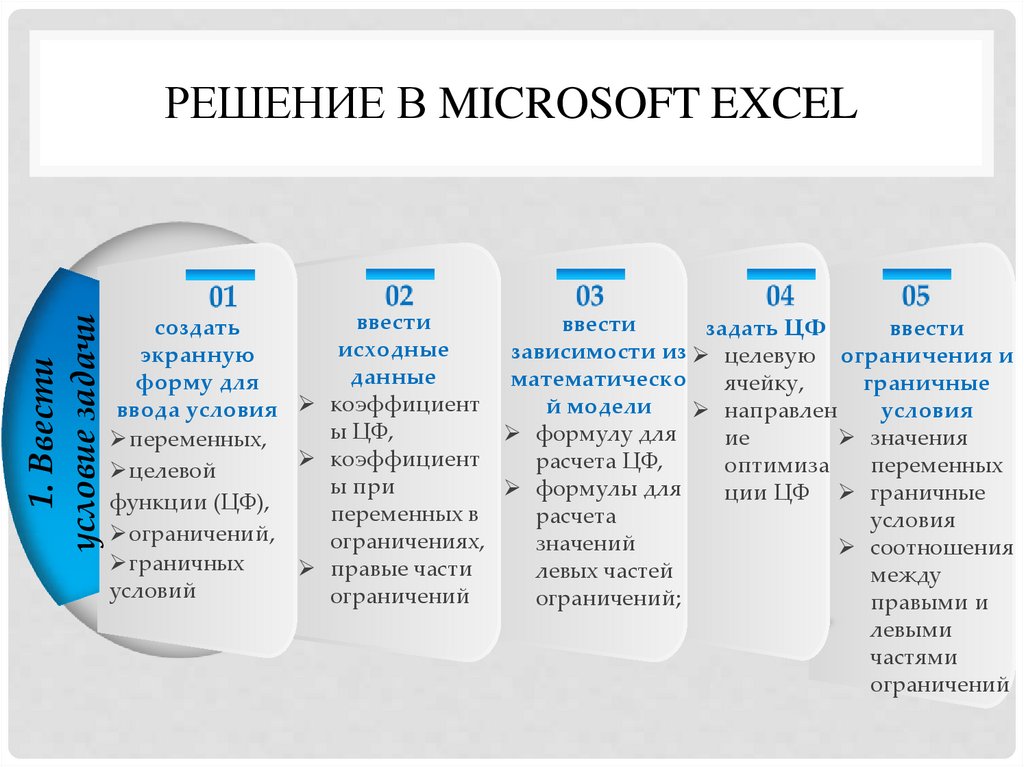
1. Ввести
условие задачи
РЕШЕНИЕ В MICROSOFT EXCEL
ввести
ввести
создать
задать ЦФ
ввести
исходные
зависимости из целевую ограничения и
экранную
данные
математическо
форму для
ячейку,
граничные
й модели
ввода условия коэффициент
направлен
условия
ы ЦФ,
формулу для
ие
значения
переменных,
коэффициент
расчета ЦФ,
оптимиза
переменных
целевой
ы при
формулы для
ции ЦФ граничные
функции (ЦФ),
переменных в
расчета
условия
ограничений,
ограничениях,
значений
соотношения
граничных
правые части
левых частей
между
условий
ограничений
ограничений;
правыми и
левыми
частями
ограничений

68.

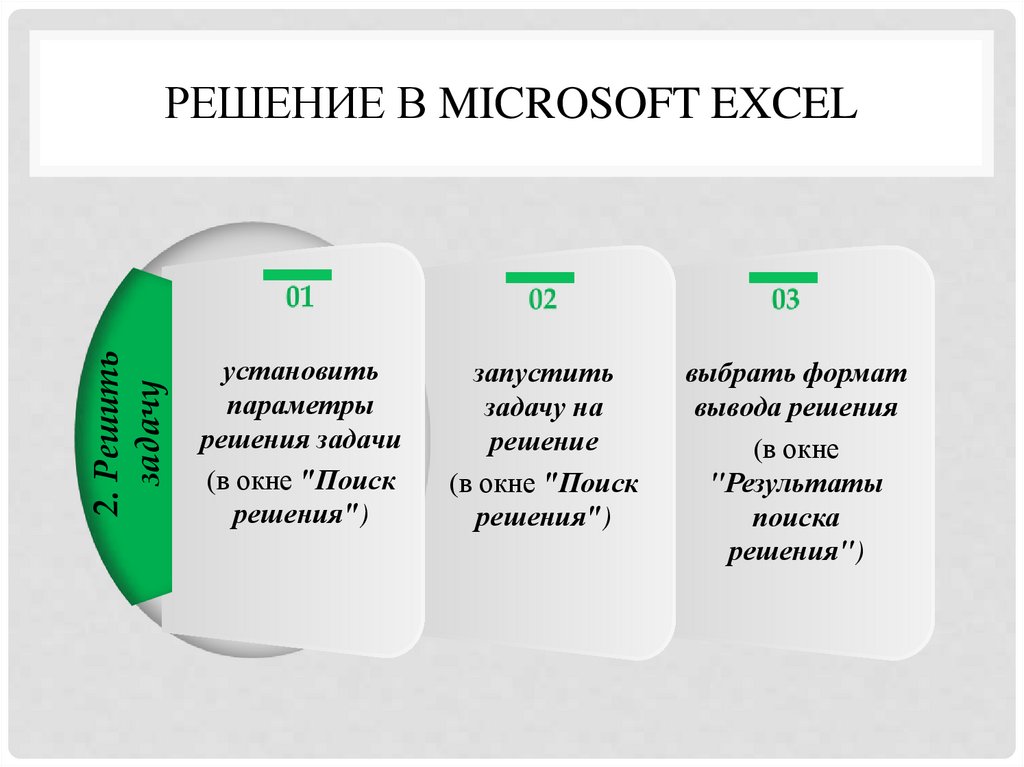
2. Решить
задачу
РЕШЕНИЕ В MICROSOFT EXCEL
установить
параметры
решения задачи
(в окне "Поиск
решения")
запустить
задачу на
решение
(в окне "Поиск
решения")
выбрать формат
вывода решения
(в окне
"Результаты
поиска
решения")

69.

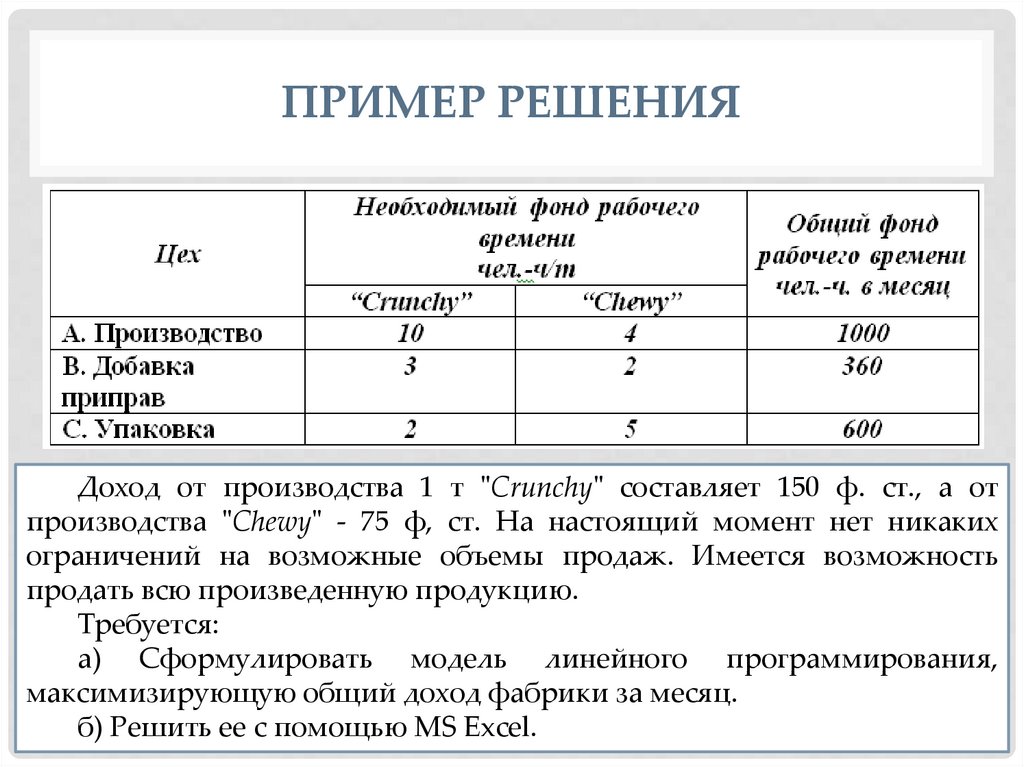
ПРИМЕР РЕШЕНИЯ
Фабрика выпускает два вида каш для завтрака "Crunchy" и "Chewy". Используемые для производства
обоих продуктов ингредиенты в основном одинаковы и,
как правило, не являются дефицитными. Основным
ограничением, накладываемым на объем выпуска,
является наличие фонда рабочего времени в каждом из
трех цехов фабрики.
Управляющему
производством
необходимо
разработать план производства на месяц. В приведенной
ниже таблице указаны общий фонд рабочего времени и
число человеко-часов, требуемое для производства 1 т
продукта.

70.

ПРИМЕР РЕШЕНИЯ
Доход от производства 1 т "Crunchy" составляет 150 ф. ст., а от
производства "Chewy" - 75 ф, ст. На настоящий момент нет никаких
ограничений на возможные объемы продаж. Имеется возможность
продать всю произведенную продукцию.
Требуется:
а) Сформулировать модель линейного программирования,
максимизирующую общий доход фабрики за месяц.
б) Решить ее c помощью MS Excel.

71.

ФОРМАЛЬНАЯ ПОСТАНОВКА
Пусть х1 – каши фирмы "Crunchy"
х2 – каши фирмы "Chewy"
150 x1 75 x 2 max
10 x1 4 x 2 1000
3 x 2 x 360
1
2
2 x1 5 x 2 600
x 0
1
x2 0

72.

РЕШЕНИЕ В EXCEL
СОЗДАНИЕ ЭКРАННОЙ ФОРМЫ И ВВОД ИСХОДНЫХ ДАННЫХ
Экранная форма

73.

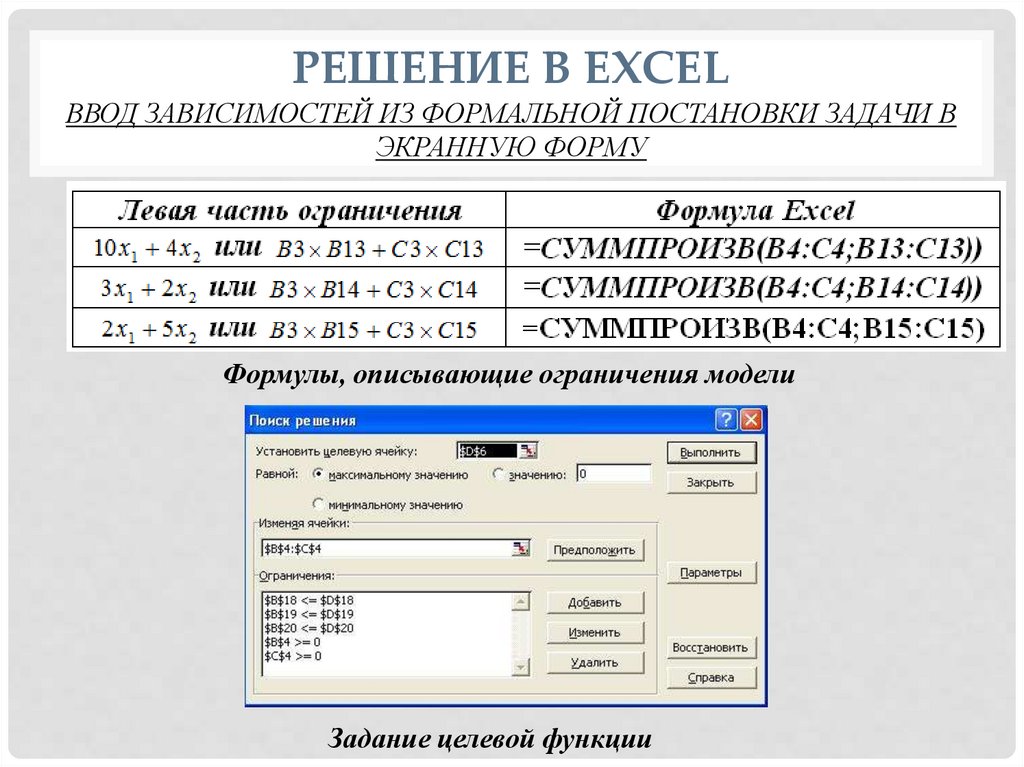
РЕШЕНИЕ В EXCEL
ВВОД ЗАВИСИМОСТЕЙ ИЗ ФОРМАЛЬНОЙ ПОСТАНОВКИ ЗАДАЧИ В
ЭКРАННУЮ ФОРМУ
Формулы, описывающие ограничения модели
Задание целевой функции

74.

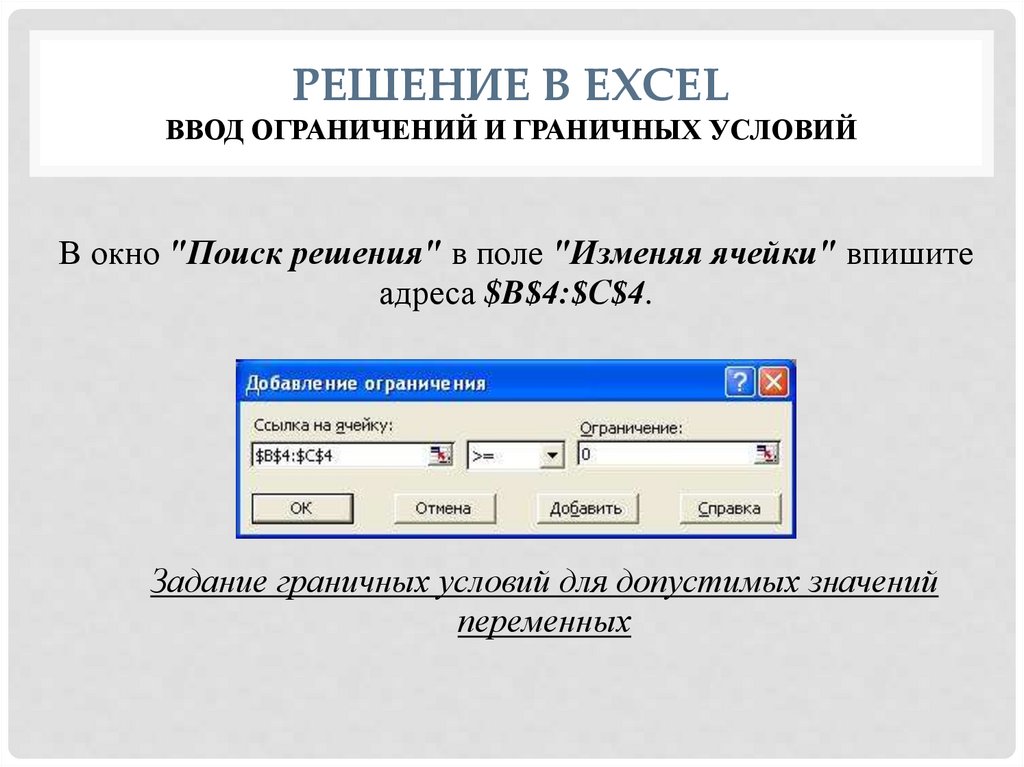
РЕШЕНИЕ В EXCEL
ВВОД ОГРАНИЧЕНИЙ И ГРАНИЧНЫХ УСЛОВИЙ
В окно "Поиск решения" в поле "Изменяя ячейки" впишите
адреса $B$4:$С$4.
Задание граничных условий для допустимых значений
переменных

75.

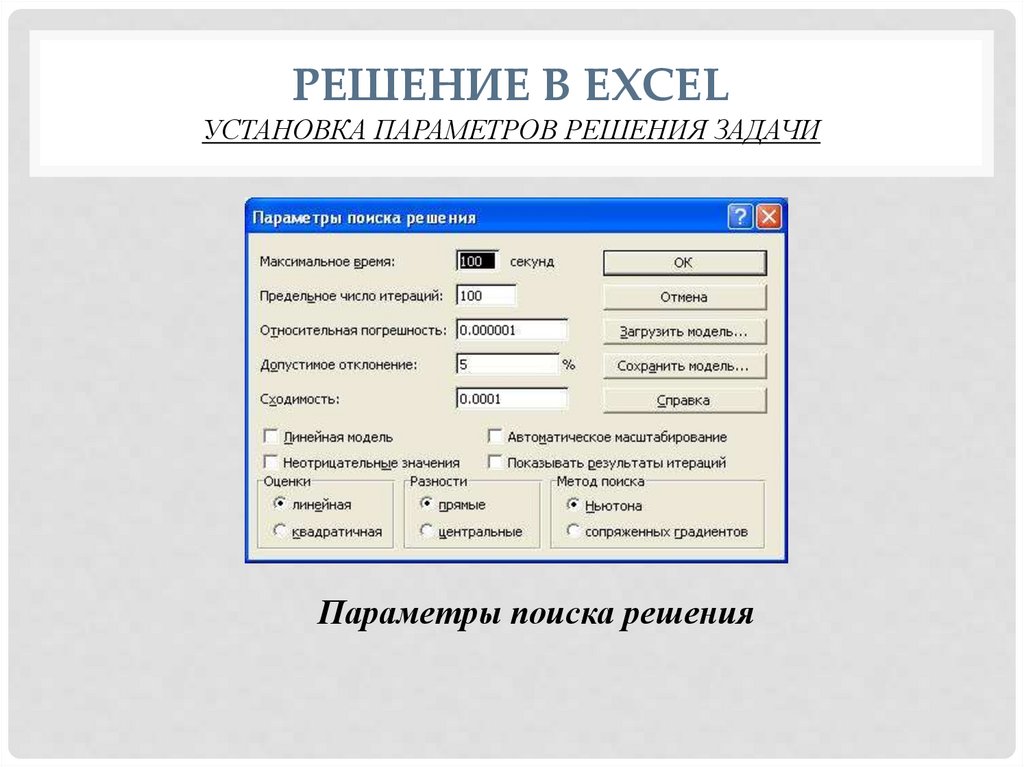
РЕШЕНИЕ В EXCEL
УСТАНОВКА ПАРАМЕТРОВ РЕШЕНИЯ ЗАДАЧИ
Параметры поиска решения

76.

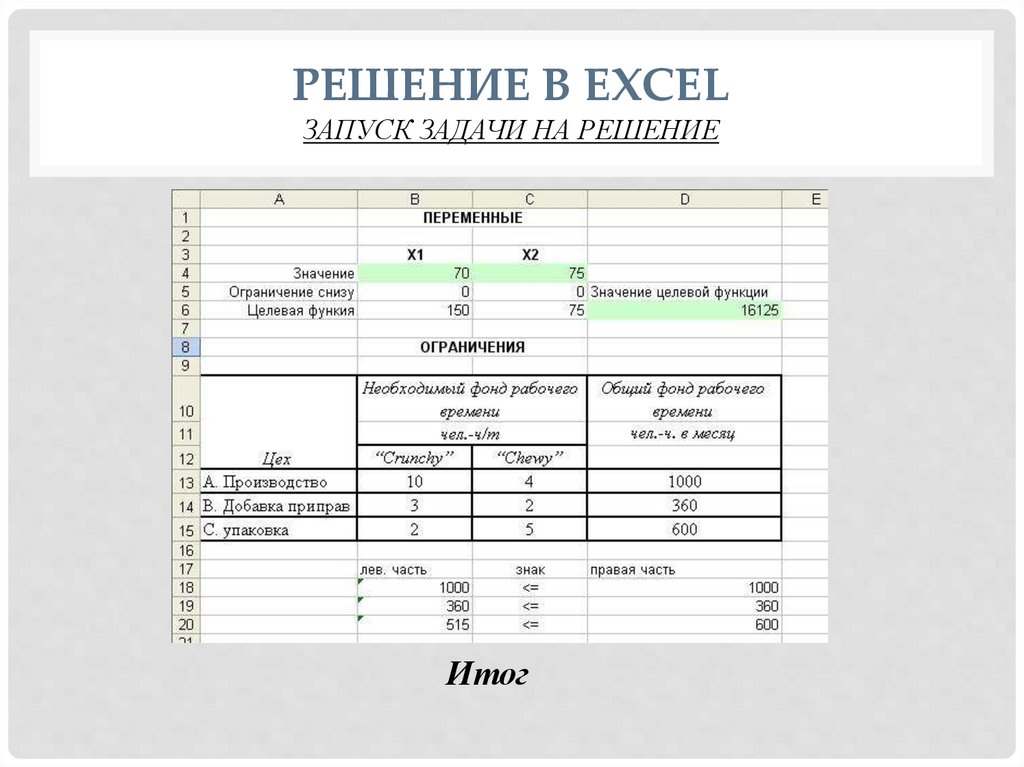
РЕШЕНИЕ В EXCEL
ЗАПУСК ЗАДАЧИ НА РЕШЕНИЕ
Итог

77.

ПОПРОБОВАТЬ САМОСТОЯТЕЛЬНО
2) Для производства двух видов продукции (А и В) используется
три типа технологического оборудования. Каждый продукт проходит
обработку на оборудовании каждого типа. Трудоемкость обработки 1
кг продукта А (в часах) на I оборудовании - 1, на II - 3, на III - 2.
Трудоемкость обработки 1 кг продукта В (в часах) на I оборудовании 5 , на II - 2, на III - 4. На изготовление всей продукции администрация
предприятия может предоставить I оборудование не более чем на 10
ч, II оборудование - не более чем на 12 ч, III оборудование - не более
чем на 10 ч.
Прибыль от реализации 1 кг готового продукта А составляет 2
тыс. р., а продукта В - 3 тыс. р.
Составить план производства продукции А и В, обеспечивающий
максимальную прибыль от их реализации.

78.

ПОПРОБОВАТЬ САМОСТОЯТЕЛЬНО
3) Для сохранения здоровья и работоспособности человек должен
потреблять в сутки определенное количество белков, жиров, углеводов, воды
и витаминов. Предположим (для простоты решения задачи), что дневной
рацион человека составляется из трех продуктов: П1, П2, ГІЗ. Стоимость этих
продуктов задана на рисунке 23. Запасы ингредиентов в различных продуктах
различны (рис. 23). Следует таким образом определить дневной рацион,
чтобы его стоимость была наименьшей, но при этом в нем содержалось
необходимое количество питательных веществ.