Приклади опрацювання результатів прямих вимірювань з багаторазовими спостереженнями. Оцінювання непевності за методом типу А

1. OPB Тема 3/7 Практична: Приклади Опрацювання результатів прямих вимірювань з багаторазовими спостереженнями. Оцінювання

непевності за методом типу А.
Виявлення та усунення впливу аномальних
спостережень (промахів)

2. Зміст

1. Приклад 1. Опрацювання для відомого
стандартного відхилення спостережень
2. Приклад 2. Опрацювання для невідомого
стандартного відхилення спостережень
3. Приклад 3. Опрацювання результатів.
Виявлення аномальних спостережень.
2
M. DOROZHOVET S

3. Приклад 1. Опрацювання для відомого стандартного відхилення спостережень

Для зменшення впливу випадкових впливів здійснено
серію з n=25 вимірювань струму І і отримано такі
результати спостережень (в мА):
4,956 4,995
4,973 5,090 5,024 4,893 4,931 5,053 5,027 4,988
5,033 5,067 5,055 5,113 4,932 4,911 4,949 5,194
4,999 4,901 5,010 5,144 5,188 5,099 5,060.
Попередні дослідження показали, що впливом
систематичних ефектів можна знехтувати,
результати спостережень практично не
корельовані, розподілені за нормальним законом, а
також відомо стандартне відхилення спостережень
рівне σ=0.080мА.
Оцінити результат вимірювання, стандартну та
розширену непевності (при р=0.95).
3
M. DOROZHOVET S

4. Приклад 1. Опрацювання для відомого стандартного відхилення спостережень

Процедура опрацювання:
1. Обчислюємо середнє значення величини як
найкращої її оцінки
2. За відомого стандартного відхилення
спостережень обчислюємо стандарну непевність
величини
3. Для заданого рівня довіри (довірчої ймовірності)
обчислюємо розширену непевність величини коефіцієнт розширення беремо з таблиці
нормального розподілу
4. Записуємо результат вимірювання у спрощеній
формі (з розширеною непевністю).
4
M. DOROZHOVET S

5. Приклад 1. Опрацювання для відомого стандартного відхилення спостережень

Розв’язання. (4,956 4,9954,9735,0905,0244,893
4,9315,0535,0274,9885,0335,0675,0555,113
4,9324,911 4,9495,1944,9994,9015,0105,144
5,1885,0995,060.)
1. Обчислюємо середнє значення струму
1 n
I I i 5.0234 мА
n i 1
5
M. DOROZHOVET S

6. Приклад 1. Опрацювання для відомого стандартного відхилення спостережень

2. Обчислюємо стандартну непевність : вона у корінь
квадратний менша від заданого (відомого)
стандартного відхилення сростережень
u A I
n
0.080 мА
0.0160 мА
25
6
M. DOROZHOVET S

7. Приклад 1. Опрацювання для відомого стандартного відхилення спостережень

3. Обчислюємо розширену непевність.
Для заданого рівня довіри р=0.95 і нормального
розроділу коефіцієнт розширення (охоплення)
становить k0.95=1.96, тому розширена непевність
U 0.95 I k0.95 u A I 1.96 0.0160 мА 0.03136 мА
7
M. DOROZHOVET S

8. Приклад 1. Опрацювання для відомого стандартного відхилення спостережень

4. Представлення результату.
4.1. Заокруглюємо розширену непевність:
0.03136 мА≈0.031 мА
(до двох значущих цифр).
4.2. Заокруглюємо результат (середнє значення):
5.0234 мА ≈5.023 мА (до тисячних часток мА як і
заокруглена непевність).
4.3. Результат вимірювання (скорочено):
І=(5.023 ± 0.031) мА, р=0.95, n=25, розп. нормальний.
8
M. DOROZHOVET S

9. Приклад 2. Опрацювання для невідомого стандартного відхилення спостережень

Для зменшення впливу випадкових впливів здійснено
серію з n=25 вимірювань струму І і отримано такі
результати спостережень (в мА) (ці самі
спостереження):
4,956 4,995 4,973 5,090 5,024
4,893 4,931 5,053 5,027 4,988 5,033 5,067 5,055
5,113 4,932 4,911 4,949 5,194 4,999 4,901 5,010
5,144 5,188 5,099 5,060.
Попередні дослідження показали, що впливом
систематичних ефектів можна знехтувати,
результати спостережень практично не
корельовані, розподілені за нормальним законом, а
стандартне відхилення спостережень невідоме.
Оцінити результат вимірювання, стандартну та
розширену непевності (при р=0.95).
9
M. DOROZHOVET S

10. Приклад 2. Опрацювання для невідомого стандартного відхилення спостережень

Процедура опрацювання:
1. Обчислюємо середнє значення величини
2. За невідомого стандартного відхилення
спостережень обчислюємо його зміщену s та
незміщену S оцінки стандартного відхилення
3. Обчислюємо приблизне значення стандарної
непевності величини
4. Уточнюємо стандартну непевність величини
5.
6.
Для заданого рівня довіри (довірчої ймовірності)
обчислюємо розширену непевність величини –
використовуємо коефіцієнт розширення з таблиці
розподілу Студента (Student)
Записуємо результат вимірювання у спрощеній
формі (з розширеною непевністю).
10
M. DOROZHOVET S

11. Приклад 2. Опрацювання для невідомого стандартного відхилення спостережень

Розв’язання.
(4,956
4,9954,9735,0905,0244,8934,9315,053
5,0274,9885,0335,0675,0555,113 4,9324,911
4,9495,1944,9994,9015,0105,1445,1885,099
5,060.)
1. Обчислюємо середнє значення струму –
воно таке саме як у попередньому прикладі
1 n
I I i 5.0234 мА
n i 1
11
M. DOROZHOVET S

12. Приклад 2. Опрацювання для невідомого стандартного відхилення спостережень

2. Оскільки стандартне відхилення спостережень
невідоме, то обчислюємо його зміщену s та
незміщену S оцінки
2
1 25
n
25
s
I
I
0
.
08269
мА
;
S
s
0
.
08269
0.08444 мА
i
25 i 1
n 1
24
12
M. DOROZHOVET S

13. Приклад 2. Опрацювання для невідомого стандартного відхилення спостережень

Розв’язання.
3. Обчислюємо приблизне значення
стандартної непевності (тут також вона у
корінь квадратний менша від оцінки
стандартного відхилення)
u A I
S
0,08444 мА
0.01688 мА
n
25
4. Точне значення стандартної непевності
uA (I )
s
0.08269
S
n 1 0.08444 25 1
0.01764 мА
0.01764 мА
25 3
n 3
25 3
n n 3
25
Різниця наближеним та точним значенням не є
істотною.
13
M. DOROZHOVET S

14. Приклад 2. Опрацювання для невідомого стандартного відхилення спостережень

5. Обчислюємо розширену непевність.
Розширену непевність знайдемо як добуток
коефіцієнта розширення , взятого із табл. квантилів
розподілу Стьюдента (оскільки стандартне
відхилення результатів спостережень було
невідомим і оцінювалося з отриманої вибірки), на
обчислену стандартну непевність .
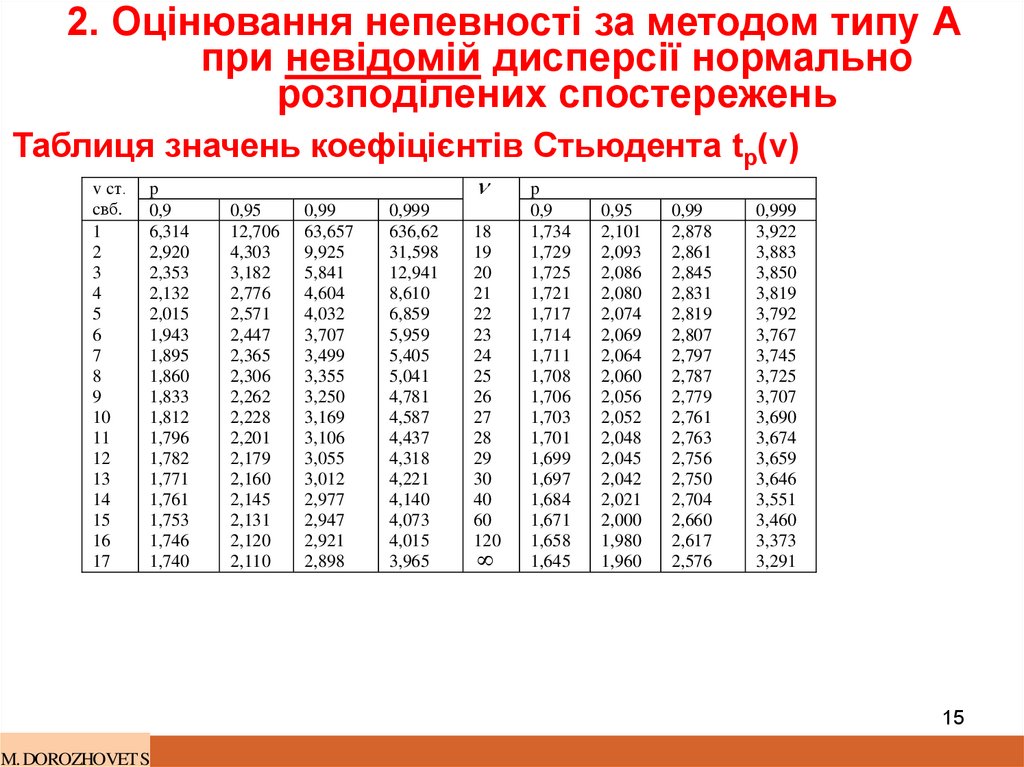
Для кількості ступенів свободи v=n-1=25-1=24 та рівня
довіри р=0.95 з табл. маємо
k0.95=t0.95(24) =2.064.
Отже, розширена непевність вимірювання струму
U 0.95 ( I ) t0.95 (24) u A ( I ) 2.064 0.016888 0.03486 мА
14
M. DOROZHOVET S

15. 2. Оцінювання непевності за методом типу А при невідомій дисперсії нормально розподілених спостережень

Таблиця значень коефіцієнтів Стьюдента tp(v)
v cт.
cвб.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
p
0,9
6,314
2,920
2,353
2,132
2,015
1,943
1,895
1,860
1,833
1,812
1,796
1,782
1,771
1,761
1,753
1,746
1,740
0,95
12,706
4,303
3,182
2,776
2,571
2,447
2,365
2,306
2,262
2,228
2,201
2,179
2,160
2,145
2,131
2,120
2,110
0,99
63,657
9,925
5,841
4,604
4,032
3,707
3,499
3,355
3,250
3,169
3,106
3,055
3,012
2,977
2,947
2,921
2,898
0,999
636,62
31,598
12,941
8,610
6,859
5,959
5,405
5,041
4,781
4,587
4,437
4,318
4,221
4,140
4,073
4,015
3,965
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
p
0,9
1,734
1,729
1,725
1,721
1,717
1,714
1,711
1,708
1,706
1,703
1,701
1,699
1,697
1,684
1,671
1,658
1,645
0,95
2,101
2,093
2,086
2,080
2,074
2,069
2,064
2,060
2,056
2,052
2,048
2,045
2,042
2,021
2,000
1,980
1,960
0,99
2,878
2,861
2,845
2,831
2,819
2,807
2,797
2,787
2,779
2,761
2,763
2,756
2,750
2,704
2,660
2,617
2,576
0,999
3,922
3,883
3,850
3,819
3,792
3,767
3,745
3,725
3,707
3,690
3,674
3,659
3,646
3,551
3,460
3,373
3,291
15
M. DOROZHOVET S

16. Приклад 2. Опрацювання для невідомого стандартного відхилення спостережень

6. Представлення результату.
6.1. Заокруглюємо розширену непевність:
0.03486 мА≈ 0.035 мА
(до двох значущих цифр).
6.2. Заокруглюємо результат (середнє значення):
5.0234 мА ≈ 5.023 мА (до тисячних часток мА як і
заокруглена непевність).
6.3. Результат вимірювання (скорочено):
І=(5.023 ± 0.035) мА, р=0.95, v=24, розп. Стьюдента.
16
M. DOROZHOVET S

17. Приклад 2. Опрацювання для невідомого стандартного відхилення спостережень

6. Представлення результату.
6.4. Більш повна форма результату вимірювання:
І=(5.023 ± 0.035) мА, р=0.95, v=24, розп. Стьюдента
знайдено як середнє значення із не корельованих,
розподілених за нормальним законом результатів
спостережень, при оціненій стандартній непевності
типу А 0.01688 мА , розширену непевність 0.03486
мА знайдено для рівня довіри р=0.95 , коефіцієнт
розширення 2.064 взято з таблиці Стьюдента при
кількості ступенів свободи 24.
Систематичними впливами на результат вимірювання
знехтувано.
17
M. DOROZHOVET S

18. Приклад 3. Опрацювання результатів. Виявлення аномальних спостережень

Для зменшення впливу випадкових впливів здійснено
серію з n=10 вимірювань напруги U і отримано такі
результати спостережень (у B): 11.982
11.973
11.981
11.962
11.955
12.002
11.995
12.022
12.113
12.032.
Попередні дослідження показали, що впливом
систематичних ефектів можна знехтувати,
результати спостережень практично не
корельовані, розподілені за нормальним законом.
Стандартне відхилення спостережень відоме
σ=0.050 В.
Перевірити на аномальність результатів з рівнем
істотності α =0.05 і зробити відповідний висновок
Оцінити стандартну та розширену непевності (при
р=0,90) і записати результат вимірювання.
18
M. DOROZHOVET S

19. Приклад 3. Опрацювання результатів. Виявлення аномальних спостережень

Процедура опрацювання: для відомого стандартного
відхилення спостережень
1. Обчислюємо середнє значення величини
2. Для виявлення аномальних результатів сортуємо
спостереження (так званий варіаційний ряд) і
визначаємо найменше (після сортування 1-ше) та
найбільше (після сортування останнє) значення
спостережнь.
3. Обчислюємо зведені до заданого стандартного
відхилення σ спостережень відхилення
найменшого (vσ1) та найбільшого (vσ2) спостережень
від середнього значення
4. Для заданої кількості cпостережень n та рівня
істотності α з таблиці для відомого σ знаходимо
допустиме значення vσdop.
19
M. DOROZHOVET S

20. Приклад 3. Опрацювання результатів. Виявлення аномальних спостережень

Процедура опрацювання: для відомого
стандартного відхилення спостережень
5. Порівнюємо обчислені вище значення (vσ1, vσ2) із
допустимим vσdop і робимо висновок:
про наявність серед отриманих результатів
аномальних спостережень (промахів)
якщо більше відхилення перевищує допустиме
значення, або
відсутність серед отриманих результатів аномальних
спостережень (промахів),
якщо більше відхилення не перевищує допустиме
значення.
20
M. DOROZHOVET S

21. Приклад 3. Опрацювання результатів. Виявлення аномальних спостережень

6. У разі виявленого аномального спостереження його
відкидають, тоді кількість спостережень
зменшується на 1 (нове значення n-1) і
опрацювання повтрюють з початку (п1).
7. Процедуру ровторюють аж до встановлення факту
відсутності аномальних спостережень:
Для заданого рівня довіри (довірчої ймовірності)
обчислюємо розширену непевність величини –
використовуємо коефіцієнт розширення з
нормального розподілу
8. Записуємо результат вимірювання у спрощеній
формі (з розширеною непевністю).
21
M. DOROZHOVET S

22. Приклад 3. Опрацювання результатів. Виявлення аномальних спостережень.

Розв’язання. Для відомого стандартного відхилення
спостережень
Вхідні дані: (11.982
11.973
11.981
11.962
11.955
12.002
11.995
12.022
12.118
12.032)
1. Обчислюємо середнє значення напруги результат
вимірювання
1 n
1 10
U U i U i 12.0022 B
n i 1
10 i 1
22
M. DOROZHOVET S

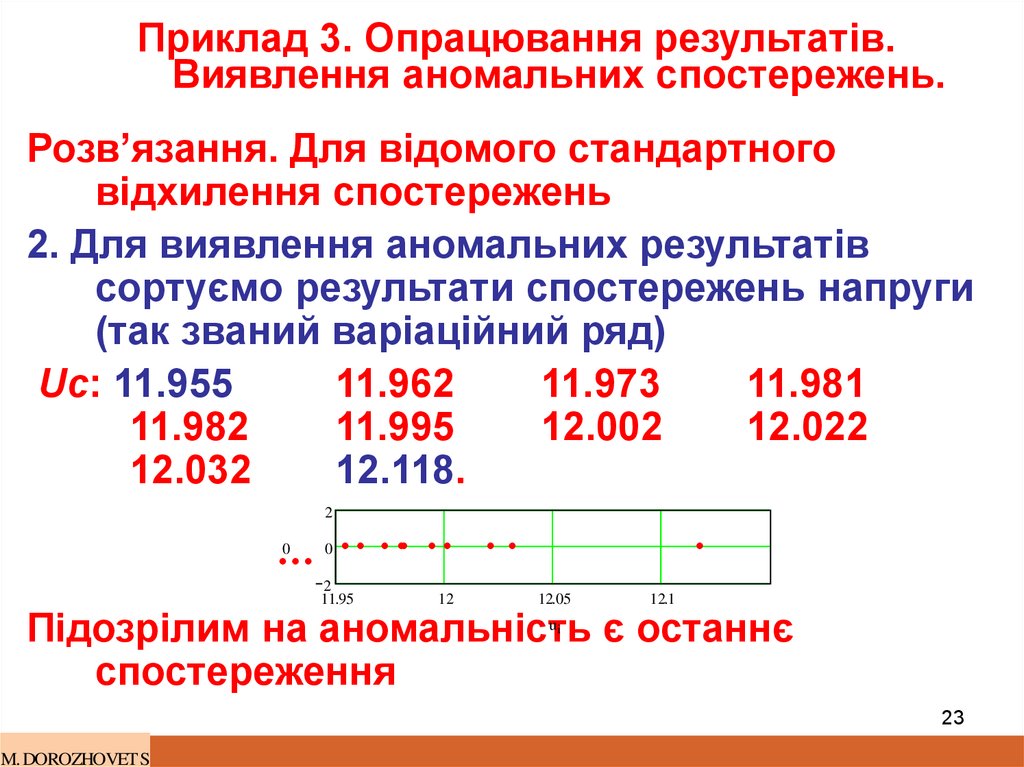
23. Приклад 3. Опрацювання результатів. Виявлення аномальних спостережень.

Розв’язання. Для відомого стандартного
відхилення спостережень
2. Для виявлення аномальних результатів
сортуємо результати спостережень напруги
(так званий варіаційний ряд)
Uс: 11.955
11.962
11.973
11.981
11.982
11.995
12.002
12.022
12.032
12.118. u xs
2
0
0
2
11.95
12
12.05
12.1
Підозрілим на аномальність є останнє
спостереження
ui
23
M. DOROZHOVET S

24. Приклад 3. Виявлення аномальних спостережень. Опрацювання результатів

3. Оскільки стандартне відхилення спостережень
відоме , то обчислюємо зведене (до стандартного
відхилення σ=0.05 B) відхилення від середнього
значення (12.0022 B) найбільшого (12.118 B) зі
спостережень (воно відхиляється від середнього
найбільше)
v ,max
U c10 U
12.118B 12.0022 B
0.05B
2.316
24
M. DOROZHOVET S

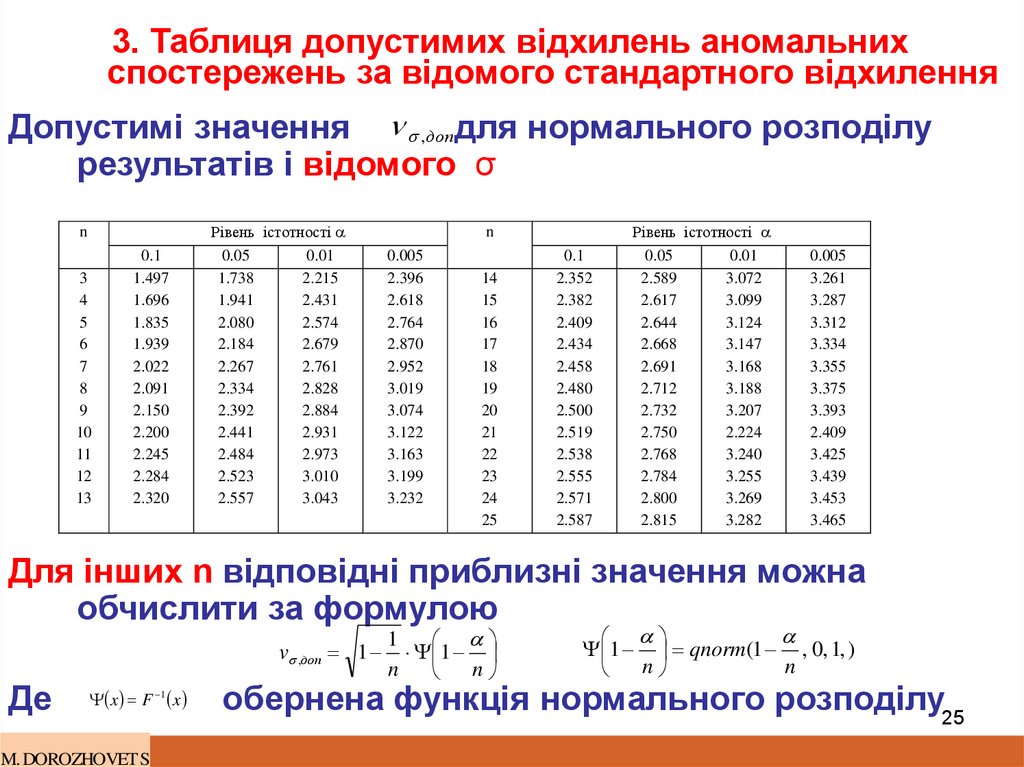
25. 3. Таблиця допустимих відхилень аномальних спостережень за відомого стандартного відхилення

Допустимі значення ,допдля нормального розподілу
результатів і відомого σ
n
3
4
5
6
7
8
9
10
11
12
13
0.1
1.497
1.696
1.835
1.939
2.022
2.091
2.150
2.200
2.245
2.284
2.320
Рівень істотності
0.05
0.01
1.738
2.215
1.941
2.431
2.080
2.574
2.184
2.679
2.267
2.761
2.334
2.828
2.392
2.884
2.441
2.931
2.484
2.973
2.523
3.010
2.557
3.043
n
0.005
2.396
2.618
2.764
2.870
2.952
3.019
3.074
3.122
3.163
3.199
3.232
14
15
16
17
18
19
20
21
22
23
24
25
0.1
2.352
2.382
2.409
2.434
2.458
2.480
2.500
2.519
2.538
2.555
2.571
2.587
Рівень істотності
0.05
0.01
2.589
3.072
2.617
3.099
2.644
3.124
2.668
3.147
2.691
3.168
2.712
3.188
2.732
3.207
2.750
2.224
2.768
3.240
2.784
3.255
2.800
3.269
2.815
3.282
0.005
3.261
3.287
3.312
3.334
3.355
3.375
3.393
2.409
3.425
3.439
3.453
3.465
Для інших n відповідні приблизні значення можна
обчислити за формулою
v ,доп 1
Де
x F 1 x
M. DOROZHOVET S
1
1
n
n
1 qnorm(1 , 0, 1, )
n
n
обернена функція нормального розподілу25

26. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень.

4. Для n=10 cпостережень та рівня істотності α
=0.05 з табл. для відомого σ знаходимо
допустиме значення vσ,dop=2.441.
5. Порівнюючи обчислене вище значення
(2.3165) із допустимим (2.441), робимо
висновок, що найбільше спостереження
(12.118) за цим критерієм не можна вважати
аномальним на рівні істотності 0.05.
26
M. DOROZHOVET S

27. Приклад 3. Опрацювання результатів. Виявлення аномальних спостережень.

6. Обчислюємо значення стандартної непевності
напруги
u A U
n
0.05 B
0.01581 B
10
7. Обчислюємо розширену непевність.
Розширену непевність знайдемо як добуток
коефіцієнта розширення , взятого із табл. квантилів
нормального розподілу (оскільки стандартне
відхилення результатів спостережень було
відомим), на обчислену стандартну непевність .
Для рівня довіри р=0.90 маємо k0.90=1.65.
Отже, розширена непевність вимірювання напруги
U 0.90 (U ) k90 u A (U ) 1.65 0.01581 0.0261 B
27
M. DOROZHOVET S

28. Приклад 3. Опрацювання результатів. Виявлення аномальних спостережень.

8. Представлення результату.
8.1. Заокруглюємо розширену непевність:
0.0261 B≈0.026 B
(до двох значущих цифр).
8.2. Заокруглюємо результат (середнє значення):
12.0022 B ≈12.002 B (до тисячних часток B як і
заокруглена непевність).
8.3. Результат вимірювання (скорочено):
U=(12.002 ± 0.026) B, р=0.90, n=10, норм. розп.
28
M. DOROZHOVET S

29. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень.

Стандартне відхилення спостережень невідоме
Для зменшення впливу випадкових впливів здійснено
серію з n=10 вимірювань напруги U і отримано такі
результати спостережень (у B): 11.982
11.973
11.981
11.962
11.955
12.002
11.995
12.022
12.113
12.032.
Попередні дослідження показали, що впливом
систематичних ефектів можна знехтувати,
результати спостережень практично не
корельовані, розподілені за нормальним законом.
Стандартне відхилення спостережень невідоме.
Перевірити на аномальність результатів з рівнем
істотності α =0.05.
Оцінити результат вимірювання, стандартну та
розширену непевності (при р=0,90).
29
M. DOROZHOVET S

30. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень

Процедура опрацювання: для невідомого стандартного
відхилення сростережень
1. Обчислюємо середнє значення величини
2. Обчислюємо оцінку стандартного відхилення
спостережень
3. Для виявлення аномальних результатів сортуємо
спостереження (так званий варіаційний ряд) і
визначаємо найменше (після сортування 1-ше) та
найбільше (після сортування останнє) значення
спостережнь.
4. Обчислюємо зведені до оцінки стандартного
відхилення s спостережень відхилення
найменшого (vs1) та найбільшого (vs2) спостережень
від середнього значення
30
M. DOROZHOVET S

31. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень

Процедура опрацювання: для невідомого стандартного
відхилення сростережень
5. Для заданої кількості cпостережень n та рівня
істотності α з таблиці для невідомого σ знаходимо
допустиме значення vs?dop.
6. Порівнюємо обчислені вище значення (vs1, vss2,
звичайно беруть більше) із допустимим vs?dop і
робимо висновок:
про наявність серед отриманих результатів
аномальних спостережень (промахів)
якщо більше відхилення перевищує допустиме
значення, або
відсутність серед отриманих результатів аномальних
спостережень (промахів),
якщо більше відхилення не перевищує допустиме
значення.
31
M. DOROZHOVET S

32. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень

Процедура опрацювання: для невідомого стандартного
відхилення сростережень
7. У разі виявленого аномального спостереження його
відкидають, тоді кількість спостережень
зиеншується на 1 (нове значення n-1) і
опрацювання повтрюють з початку (п1).
8. Процедуру ровторюють аж до встановлення факту
відсутності аномальних спостережень.
9. Для заданого рівня довіри (довірчої ймовірності)
обчислюємо розширену непевність величини –
використовуємо коефіцієнт розширення з таблиці
розподілу Студента (Student)
10. Записуємо результат вимірювання у спрощеній
формі (з розширеною непевністю).
32
M. DOROZHOVET S

33. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень.

Розв’язання. Для невідомого стандартного
відхилення спостережень
Вхідні дані: (11.982 11.973
11.981
11.962
11.955
12.002
11.995
12.022
12.118
12.032)
1. Обчислюємо середнє значення напруги
результат вимірювання
1 n
1 10
U U i U i 12.0022 B
n i 1
10 i 1
33
M. DOROZHOVET S

34. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень.

Розв’язання. Для невідомого стандартного відхилення
спостережень
2. Для виявлення аномальних результатів сортуємо
результати спостережень напруги (так званий
варіаційний ряд)
Uс: 11.955 11.962
11.973
11.981
11.982
11.995
12.002 u xs 12.022
12.032
12.118.
2
0
0
2
11.95
12
12.05
12.1
u
Підозрілим на аномальність є останнє
спостереження
i
34
M. DOROZHOVET S

35. Приклад 4. Виявлення аномальних спостережень. Опрацювання результатів

Розв’язання. Для невідомого стандартного відхилення
спостережень
3. Оскільки стандартне відхилення спостережень
невідоме, то обчислюємо його зміщену s оцінку
2
1 10
s
U
U
0.04505 B
i
10 i 1
4. Обчислюємо зведену (до оцінки стандартного
відхилення s=0.04505 B) відхилення від середнього
значення найбільшого зі спостережень (воно
відхиляється від середнього найбільше)
vS
U c10 U
s
12.118B 12.0022 B
0.04505B
2.5705
35
M. DOROZHOVET S

36. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень.

Для невідомого стандартного відхилення
спостережень
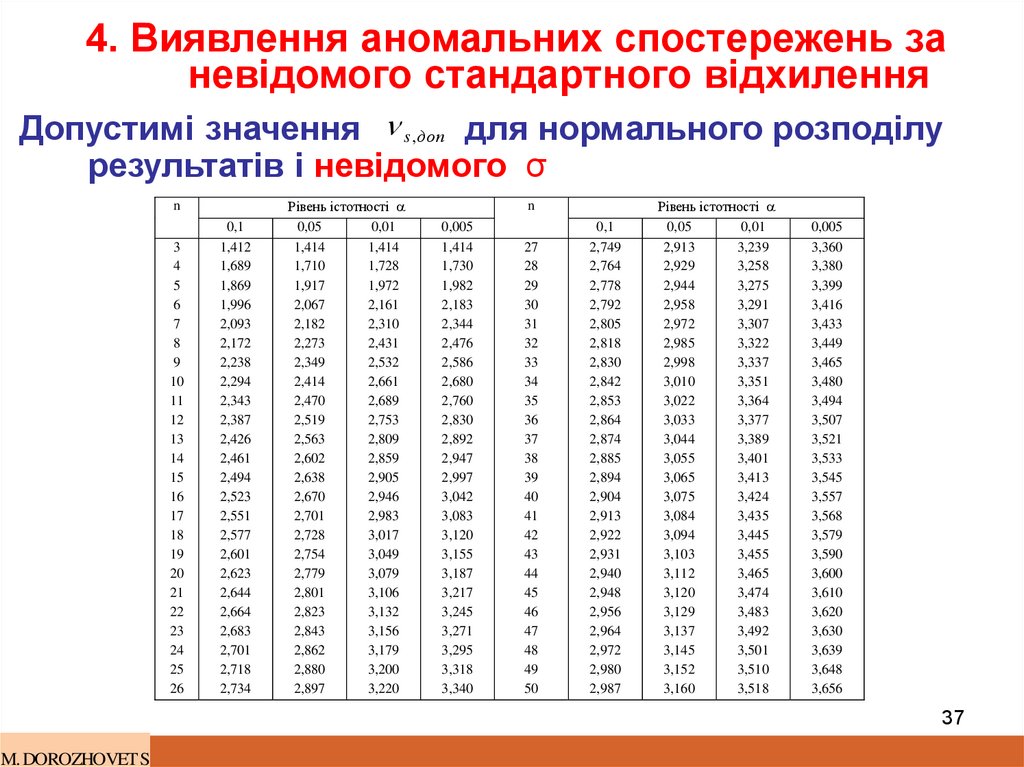
5. Для n=10 cпостережень та рівня істотності α =0.05 з
табл. для невідомого σ знаходимо допустиме
значення vS,dop=2.414.
6. Порівнюючи обчислене вище значення (2.5705) із
допустимим (2.414), робимо висновок, що
найбільше спостереження (12.118) за цим критерієм
слід вважати аномальним на рівні істотності 0.05.
Слід зазначити, що на рівні істотності 0.1
(ймовірність 10%) це спостереження також слід
вважати аномальним, натомість при (рівні
істотності 0.01 (ймовірність 1%) це спостереження
не можна вважати аномальним.
36
M. DOROZHOVET S

37. 4. Виявлення аномальних спостережень за невідомого стандартного відхилення

Допустимі значення s,доп для нормального розподілу
результатів і невідомого σ
n
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
0,1
1,412
1,689
1,869
1,996
2,093
2,172
2,238
2,294
2,343
2,387
2,426
2,461
2,494
2,523
2,551
2,577
2,601
2,623
2,644
2,664
2,683
2,701
2,718
2,734
Рівень істотності
0,05
0,01
1,414
1,414
1,710
1,728
1,917
1,972
2,067
2,161
2,182
2,310
2,273
2,431
2,349
2,532
2,414
2,661
2,470
2,689
2,519
2,753
2,563
2,809
2,602
2,859
2,638
2,905
2,670
2,946
2,701
2,983
2,728
3,017
2,754
3,049
2,779
3,079
2,801
3,106
2,823
3,132
2,843
3,156
2,862
3,179
2,880
3,200
2,897
3,220
n
0,005
1,414
1,730
1,982
2,183
2,344
2,476
2,586
2,680
2,760
2,830
2,892
2,947
2,997
3,042
3,083
3,120
3,155
3,187
3,217
3,245
3,271
3,295
3,318
3,340
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
0,1
2,749
2,764
2,778
2,792
2,805
2,818
2,830
2,842
2,853
2,864
2,874
2,885
2,894
2,904
2,913
2,922
2,931
2,940
2,948
2,956
2,964
2,972
2,980
2,987
Рівень істотності
0,05
0,01
2,913
3,239
2,929
3,258
2,944
3,275
2,958
3,291
2,972
3,307
2,985
3,322
2,998
3,337
3,010
3,351
3,022
3,364
3,033
3,377
3,044
3,389
3,055
3,401
3,065
3,413
3,075
3,424
3,084
3,435
3,094
3,445
3,103
3,455
3,112
3,465
3,120
3,474
3,129
3,483
3,137
3,492
3,145
3,501
3,152
3,510
3,160
3,518
0,005
3,360
3,380
3,399
3,416
3,433
3,449
3,465
3,480
3,494
3,507
3,521
3,533
3,545
3,557
3,568
3,579
3,590
3,600
3,610
3,620
3,630
3,639
3,648
3,656
37
M. DOROZHOVET S

38. Приклад 3. Опрацювання результатів. Виявлення аномальних спостережень

Невідоме стандартне відхилення спостережень
7. Оскільки найбільше спостереження (12.118)
за цим критерієм на рівні істотності 0.05
слід вважати аномальним, то його
відкидаємо для 10-1=9 спостережень
обчислюємо нове середнє значення
1 9
U Uci 11.98933 B
9 i 1
38
M. DOROZHOVET S

39. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень.

Невідоме стандартне відхилення спостережень
8. Обчислюємо нові значення зміщеної s’ та незміщеної
S’ оцінок стандартного відхилення спостережень
2
2
1 9
1 9
s
Uci U 0.02448 B; S
Uci U 0.02597 B
9 i 1
9 1 i 1
9. Обчислюємо зведені (до оцінки стандартного
відхилення s’=0.02448 В) відхилення від середнього
значення найменшого (11.955) та найбільшого
(12.032) спостережень: (11.955 11.962
11.973
11.981
11.982
11.995
12.002
12.022
12.032)
vS ,1
U c1 U
s
11.955B 11.98933 B
0.02448B
1.402 vs ,9
U c9 U
s
12.032 B 11.98933 B
0.02448B
1.743
39
M. DOROZHOVET S

40. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень.

Невідоме стандартне відхилення спостережень
10. Для n1=9 cпосрережень та рівня істотності α =0.05 з
табл. для невідомого σ знаходимо допустиме
значення vs,dop=2.349.
Порівнюючи обчислені вище значення (1.402 i 1.743) із
допустимим (2.349), робимо висновок, що за цим
критерієм серед результатів, що залишилися,
аномальні (промахи) на рівні істотності 0.05
відсутні.
11. Обчислюємо приблизне значення стандартної
непевності напруги
S
0.02597 B
u A U
n1
9
0.008657 B
Точне значення стандартної непевності напруги
u A (U )
s
S
n1 1 0.02597 B 9 1
0.009996 B
9 3
n1 3
n1 n1 3
9
Різниця є істотною – різниця понад 13%.
M. DOROZHOVET S
40

41. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень.

Невідоме стандартне відхилення спостережень
12. Обчислюємо розширену непевність.
Розширену непевність знайдемо як добуток
коефіцієнта розширення , взятого із табл. квантилів
розподілу Стьюдента (оскільки стандартне
відхилення результатів спостережень було
невідомим і оцінювалося з отриманої вибірки), на
обчислену стандартну непевність .
Для кількості ступенів свободи v=n1-1=9-1=8 та рівня
довіри р=0.90 з табл. маємо k0.90=t0.90(8) =1.860.
Отже, розширена непевність вимірювання напруги
U 0.90 (U ) t90 (8) u A (U ) 1.860 0.008657 0.01610 B
41
M. DOROZHOVET S

42. Приклад 4. Опрацювання результатів. Виявлення аномальних спостережень.

Невідоме стандартне відхилення спостережень
13. Представлення результату.
13.1. Заокруглюємо розширену непевність:
0.01610 B≈0.016 B
(до двох значущих цифр).
13.2. Заокруглюємо результат (середнє значення):
11.98933 B ≈11.989 B (до тисячних часток B як і
заокруглена непевність).
13.3. Результат вимірювання (скорочено):
U=(11.989 ± 0.016) B, р=0.90, v=8, розп. Стьюдента.
42
M. DOROZHOVET S

43. Приклад 5. Опрацювання для невідомого стандартного відхилення спостережень

Продовження прикладу 2 для невідомого стандартного
відхилення спостережень
1. Середнє значення струму (1) обчислено у прикладі 2:
1 n
I I i 5.0234 мА
n i 1
2. Зміщену s та незміщену S оцінки стандартного
відхилення спостережень також обчислено у
прикладі25 2:
2
1
n
25
s
I
I
0.08269 мА; S s
0.08269
0.08444 мА
i
25 i 1
n 1
24
3. Обчислюємо зведені (до зміщеної] оцінки
стандартного відхилення s=0.08269 мА) відхилення
від середнього значення (5.0234) найменшого
(4.983) та найбільшого (5.194) спостережень
vS ,1
I c1 I
S
4.983 мА 5.0234 мА
0.08269 мА
1.576 vS , 25
I c 25 I
s
5.194 мА 5.0234 мА
0.08269 мА
2.062
43
M. DOROZHOVET S

44. Приклад 3. Опрацювання для невідомого стандартного відхилення спостережень

Продовження прикладу 2 для невідомого стандартного
відхилення спостережень
4. Для n=25 cпосрережень та рівня істотності α =0.05 з
табл. для невідомого σ знаходимо допустиме
значення vs,dop=2.880.
Порівнюючи обчислені вище значення (1.576, 2.062) із
допустимим (2.880), робимо висновок, що за цим
критерієм серед отриманих результатів аномальні
(промахи) ймовірно відсутні.
5. Оскільки не виявлено аномальних спостережень, то
оцінка стандартної та розширеної непевностейб а
таккож представлення результату залишаєтьсябез
змін як у прикладі 2.
44
M. DOROZHOVET S