Моделирование, виды моделей. Событие и вероятность. Лекция 1

1.

МОДЕЛИРОВАНИЕ, ВИДЫ МОДЕЛЕЙ.
СОБЫТИЕ И ВЕРОЯТНОСТЬ
Лекция 1.
Автор Зеливянская Ольга Евгеньевна

2.

Моделирование, виды моделей

3.

Материальные системы
Материальные
системы
Хорошо
организованные
Плохо
организованные

4.

Хорошо организованные системы
состоят из ограниченного количества элементов, между которыми
существуют строго определенные и однозначные зависимости.
К этим системам можно отнести простейшие химические и
физические процессы, механизмы, приборы и т.п.
Их свойства и состояния могут быть количественно описаны
с помощью законов физики и химии.

5.

Плохо организованные системы
Относятся сложные природные объекты и явления, на состояние и
свойства которых влияет множество факторов различной природы.
Типичными плохо организованными системами являются живые
организмы и их сообщества, а также большинство объектов,
изучаемых науками о Земле.
При изучении них систем в их структуре удается установить лишь
отдельные закономерности, то есть тенденции, не поддающиеся
строгому количественному выражению.

6.

Изучение плохо организованных систем
Основным методом изучения плохо организованных систем
является моделирование, когда непосредственный объект
изучения заменяется его упрощенным аналогом – моделью.

7.

Модель –
это объект, который обладает некоторыми свойствами другого
объекта (оригинала) и используется вместо него.

8.

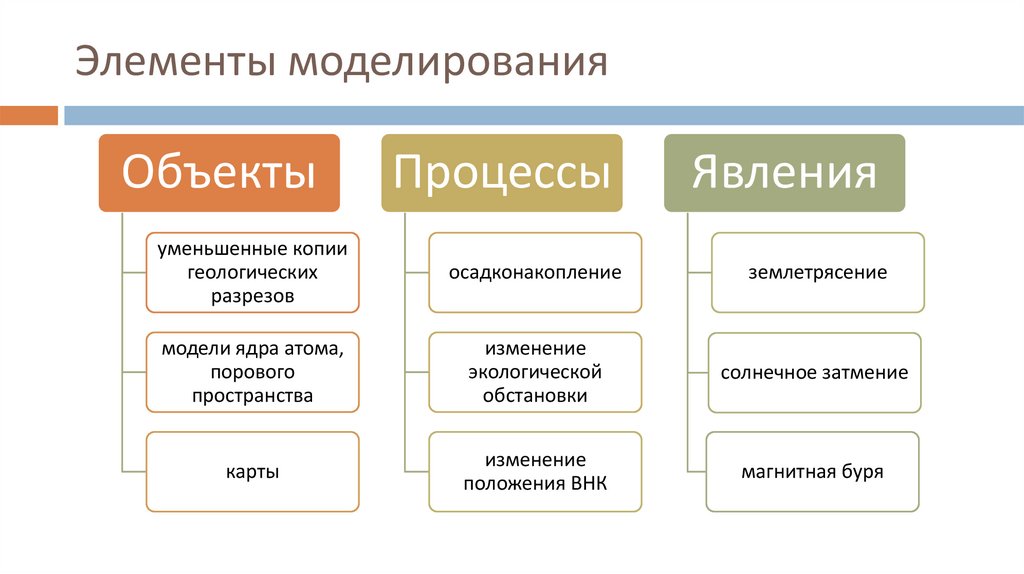
Элементы моделирования
Объекты
Процессы
Явления
уменьшенные копии
геологических
разрезов
осадконакопление
землетрясение
модели ядра атома,
порового
пространства
изменение
экологической
обстановки
солнечное затмение
карты
изменение
положения ВНК
магнитная буря

9.

Цели моделирования
исследование
оригинала
анализ
(«что будет, если …»)
синтез
(«как сделать, чтобы …»)
оптимизация
(«как сделать лучше»)
• изучение сущности объекта или явления
• научиться прогнозировать последствия различных
воздействиях на оригинал
• научиться управлять оригиналом, оказывая на него
воздействия
• выбор наилучшего решения в заданных условиях

10.

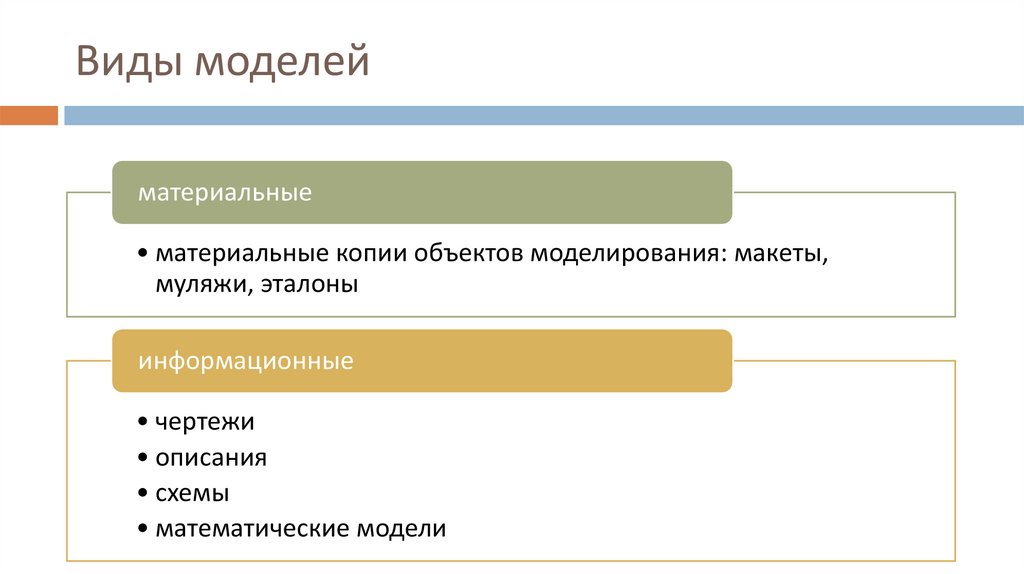
Виды моделей
материальные
• материальные копии объектов моделирования: макеты,
муляжи, эталоны
информационные
• чертежи
• описания
• схемы
• математические модели

11.

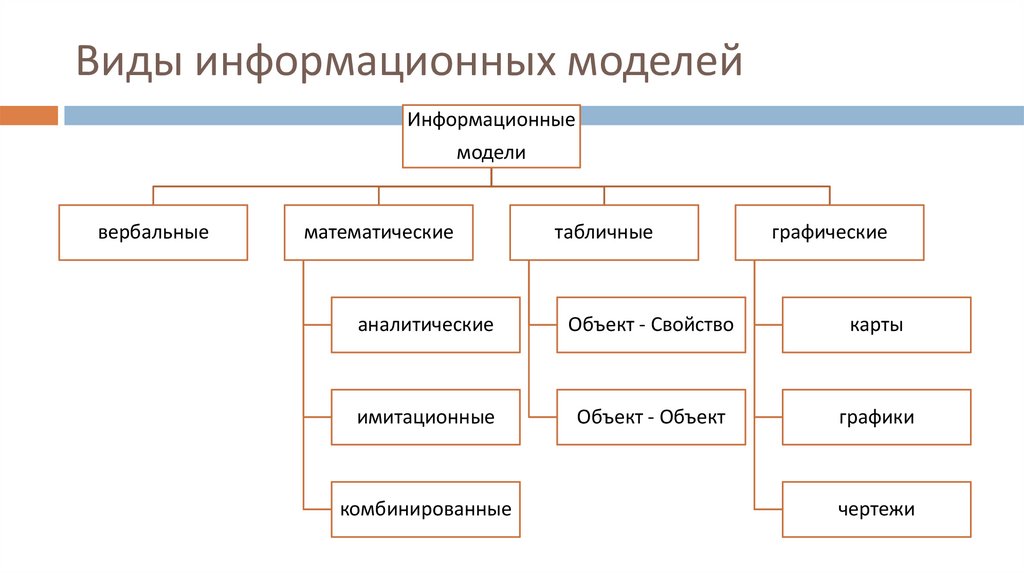
Виды информационных моделей
Информационные
модели
вербальные
математические
табличные
графические
аналитические
Объект - Свойство
карты
имитационные
Объект - Объект
графики
комбинированные
чертежи

12.

Модели по фактору времени
по фактору
времени
статические
динамические

13.

Модели по характеру связей
По характеру
связей
детерминированные
вероятностные
(стохастические)
Детерминированные - связи
между входными и выходными
величинами жестко заданы;
при одинаковых входных
данных каждый раз получаются
одинаковые результаты
Вероятностные
(стохастические) учитывают
случайность событий в
реальном мире; при
одинаковых входных данных
каждый раз получаются
немного разные результаты

14.

Этапы создания матмодели
качественные
(концептуальные)
Модели
количественные
(математические)

15.

Качественная модель
Первый этап создания модели –
выявление компонент и движущих факторов.
В геофизике это поле, источники поля и параметры среды.
Сам факт отбора этих объектов свидетельствует об их априорно
известной связи.
Исследователю эта связь часто известна только качественно
(больше - меньше, слабее - сильнее).
Качественные модели строят лишь для наименее
изученных явлений.

16.

Количественная модель
Создаются для сравнительно хорошо изученных явлений.
Компоненты формализованы - в виде чисел.
Объекты модели заменены математическими понятиями
функциями, аргументами, константами.
Количественная модель также называется математической.

17.

Математическое моделирование
в геофизике –
анализ математической модели,
включающий изучение постановки задачи, выбор класса моделей,
решение прямых задач для данных моделей.

18.

Прямая задача в геофизике расчет аномального физического поля по известным параметрам
возмущающего объекта.
Параметры объекта: расположение объекта и физические
свойства.
Прямая задача магниторазведки
для однородного шара
Исходные параметры: глубина залегания центра
шара h, радиус шара R, намагниченность J.
Вычисляются вертикальная и горизонтальная
составляющие магнитного поля Za и На

19.

Прямая задача решается однозначно – то есть имеет только одно
решение.
Прямую задачу решают на стадии проектирования работ.
Исходя из полученной ожидаемой аномалии выбирают
соответствующие аппаратуру и методику наблюдений.

20.

Математическая модель геофизического поля
В модели поля выбор измеряемых характеристик и источников
поля полностью определен методом геофизической разведки,
результаты которого интерпретируют.
Неизвестный объект модели поля – распределение параметров
среды.

21.

Обратная задача геофизики
расчет параметров и условий залегания аномалиеобразующего
объекта по измеренной геофизической аномалии.
Обратную задачу решают на этапе интерпретации
Обычно имеет несколько возможных вариантов решения, так как
одному распределению поля может отвечать множество разрезов.

22.

Событие и вероятность

23.

События
Наблюдаемые
события
Достоверные
Невозможные
Случайные

24.

Комплекс условий
Каждый эксперимент, состоящий из серии любых геофизических
измерений, сопровождается соблюдением определенного
комплекса условий.
Комплекс условий, включающий аппаратуру и методику
измерений, должен оставаться неизменным
на протяжении всего эксперимента.

25.

Случайное событие событие которое при соблюдении комплекса условий может как
произойти, так и не произойти.

26.

События в геофизике:
появление конкретного значения физического параметра или
физического поля
появление аномалии какого-либо поля
факт соответствия определенных значений поля конкретному
типу горных пород
и другие

27.

Случайные события в геофизике
Полученные отдельные значения при измерениях целесообразно
рассматривать именно как случайные события в виду случайности
расположения геологических объектов, обусловливающих
появление конкретных значений поля, случайности расположения
точек наблюдений по площади исследований и наложения помех,
вызванных разнообразными причинами, случайности отбора
образцов.

28.

Достоверное и невозможное событие
Достоверное событие – это событие, которое при том же
комплексе условий эксперимента обязательно происходит
Невозможное событие – то, которое заведомо не может
произойти при этом комплексе условий.
Факт измерения значения полного вектора магнитного поля в диапазоне от 0,33 до 0,66 Э
является достоверным событием, а, наоборот, измерение значения поля свыше 0,66 Э (или
ниже 0,33 Э) будет невозможным событием, поскольку такой величины полного вектора
магнитного поля на Земле не существует.

29.

Несовместные события
Два события называются несовместными,
если появление одного из них исключает появление другого при
одном и том же эксперименте
Наличие и отсутствие аномалии какого-либо физического поля в одной и той
же точке наблюдения – несовместные события.

30.

Суммой событий
называется событие, состоящее в появлении хотя бы одного из
несовместных событий.
Допустим, диапазон измеренных значений поля разбит на n градаций. Событие, состоящее в
появлении значения поля из первых двух градаций будет суммой двух событий, первое из
которых – появление значений из первой градации, второе – появление значений из второй
градации. Соответствующее утверждение можно высказать о сумме трех, четырех, ..., n
событий.

31.

Произведением событий
называется событие, состоящее в совместном появлении всех
несовместных событий.

32.

Пример суммы и произведения событий
Событие А - значения магнитного поля Z от 0 до 100 нТл соответствуют
гранитам
Событие В – значения поля Z от 50 до 200 нТл соответствуют
измененным породам
Событие А В – значения поля Z от 50 до 100 нТл, соответствующие
измененным разновидностям гранитов
Событие А+В – значения поля Z от 0 до 200 нТл, соответствующие или
значениям поля Z гранитов, или значениям поля Z измененных пород,
или значения полям Z измененных разновидностей гранитов.
События А и В являются совместными.

33.

Полная группа событий
События A1, А2,…, Ап образуют полную группу событии, если они
попарно несовместны, а в сумме образуют достоверное событие,
т. е. какое-либо из них обязательно происходит, причем только
одно.
Пример полной группы событий - n градаций, на которые разбит весь диапазон измеренных
значений поля.

34.

Противоположные события
два несовместных события, образующих полную группу, например
наличие и отсутствие аномалии какого-либо поля являются
противоположными событиями.
Противоположными событиями будут значения поля из первой градации и значения поля из
всех остальных градаций, на которые разбит диапазон значений поля.

35.

Вероятность события Р(А) количественная мера степени объективной возможности того или иного
события А.
Р(А)=m/n
m – число благоприятствующих событию А исходов
n – число всех равновозможных исходов экспериментов
Это классическое определение вероятности.
Оно сводит понятие вероятности к понятию равновозможных событий и исходит из соображений
симметрии (примеры с с бросанием монеты или игральной кости).
Однако задачи, связанные с симметрией эксперимента, на практике встречаются весьма редко,
например, вероятность распада атома за конечный отрезок времени на основании симметрии
определить нельзя.

36.

Статистическое определение вероятности вероятность события это относительная частота его появления при
многократном воспроизведении комплекса условий эксперимента.
При большом числе опытов частота события А стремится к вероятности Р(А) в ее классическом
определении.
Следовательно, при статистическом определении вероятность события находится лишь при
достаточно многочисленных опытах, что является недостатком этой статистической вероятности.

37.

Условная вероятность Р(А/В) вероятность события А, вычисленная при условии, что произошло
событие В.
Допустим, событие А состоит в наличии гранитов на некоторой площади исследований и
вероятность их встречи равна Р(А). После проведения геофизических измерений
(эксперимента), фиксирующих аномальными значениями поля распространение гранитов, в
чем состоит событие В, вероятность встречи гранитов Р(А) переоценивается и становится
равной Р(А/В).

38.

Независимые события
Два события называются независимыми,
если появление одного из них не изменяет вероятности появления
другого, т. е. для независимых событий Р(А/В)=Р(А),
а для зависимых Р(А/В) Р(А).

39.

Формула полной вероятности
Позволяет определить вероятность события А, происходящего
вместе с одним из событий Н1, Н2,.., Нn, образующих полную группу.
События Н1, Н2,.., Нn часто называют гипотезами.
п
Р( А) P( H i ) P( A / H i )
i 1

40.

Формула Бейеса (теорема гипотез, формула
обратных вероятностей)
п
Р( H i / А) P( H i ) P( A / H i ) / P( H i ) P( A / H i )
i 1
На основе формулы Бейеса решается задача о нахождении
вероятности Р(Нi/ А) гипотезы Нi при условиях, что в результате
проведенного эксперимента произошло событие А, а гипотезы Н1,
Н2,.., Нп образуют полную группу, причем их вероятности до опыта
известны и равны соответственно Р(Н1), Р(Н2), ..., Р(Hn).

41.

Применения формулы Бейеса
переоцениваются вероятности гипотез Р(Hi), называемые
априорными, т. е. известными (или заданными) до опыта. После
проведенного эксперимента, в результате которого появилось
событие А, вероятностей Р(Hi) изменяются. Новые вероятности
Р(Hi/A) называют апостериорными,
т. е. полученными после эксперимента.
решаются задачи выделения сигналов на фоне помех, обработки
данных комплекса геофизических полей, определения
параметров источников аномалий при количественной
интерпретации и др.