Критерий согласия Пирсона

1.

§ 14. Критерий согласия Пирсона
Для ответа на вопрос, противоречат ли опытные данные гипотезе о
том, что случайная величина X распределена по тому или иному закону,
часто используется критерий согласия 2 Пирсона. Рассмотрим этот
критерий подробнее.
Дискретная случайная величина. Рассмотрим применение критерия
Пирсона в случае дискретной случайной величины X с возможными
значениями x1 , x2 , ..., xi , ..., xr . Пусть произведено n независимых опытов,
в каждом из которых случайная величина X приняла определенное
значение, и на основе этих опытов составлен статистический ряд
распределения случайной величины X (табл. 32).
Таблица 32
x1
x2
…
xi
…
xr
p1*
p2*
…
p i*
…
pr*

2.

ni *
– относительная частота события X xi , ni* – число
n
значений в i-м разряде – число опытов, в которых произошло событие
X xi , i 1, 2, ..., r .
Выдвинем гипотезу H, что случайная величина X имеет
гипотетический ряд распределения (табл. 33).
где pi *
Таблица 33
x1
x2
…
xi
…
xr
p1
p2
…
pi
…
pr
а отклонения относительных частот
объясняются случайными причинами.
pi * wi * от вероятностей pi

3.

Для проверки правдоподобности гипотезы выберем в качестве меры
расхождения
R
статистического
(полученного
на
основе
экспериментальных данных) распределения с гипотетическим
распределением сумму квадратов отклонений pi * pi статистических
вероятностей pi* от гипотетических вероятностей pi, взятых с
некоторыми весами ci:
r
R ci p i * p i .
2
i 1
Коэффициенты ci введены для учета того, что отклонения,
относящиеся к разным значениям pi, нельзя считать равноправными по
значимости: одно и то же по абсолютной величине отклонение pi * pi
может быть малозначительным, если вероятность pi велика, и очень
заметным, если вероятность pi мала. Поэтому вполне естественно
положить веса ci обратно пропорциональными вероятностям pi.

4.

Пирсон доказал, что если положить
n
ci ,
pi
то при большом числе опытов n закон распределения величины R
практически не зависит от закона распределения случайной величины X
и мало зависит от числа проведенных опытов n, а зависит только от
числа значений r случайной величины X и при увеличении числа опытов
n приближается к распределению 2 . В этом случае меру расхождения R
обозначают символом 2 и пишут
2
r
r
r
n
p
*
p
n
p
*
p
np
*
np
n * npi .
i
i
i
i
i
2
i
i
pi
npi
npi
npi
i 1
i 1
i 1
i 1
r
2
2
2
2
Распределение 2 (рассмотрено в главе 1, § 33) зависит от параметра k –
числа степеней свободы. Это число равно числу разрядов r значений
случайной величины X за вычетом числа независимых условий (связей),
наложенных на частоты pi * . Такими условиями могут быть:

5.

r
1)
pi * 1 – требование, чтобы сумма относительных частот
i 1
равна единице (это условие накладывается всегда).
r
2) xi pi * M X – требование, чтобы статистическое среднее
i 1
совпадало с гипотетическим средним,
r
3)
2
x
m
*
i x pi * D( X ) – требование, чтобы статистическая
i 1
дисперсия совпадала с гипотетической дисперсией, и т.д.
Таким образом, максимальное значение k равно
k r 1.
Пользуясь таблицами распределения 2 можно для каждого значения 2
и числа степеней свободы k найти вероятность p того, что величина,
распределенная по закону 2 , превзойдет это значение. Входными
данными в этой таблице являются значение вероятности p и число
степеней свободы k. Числа в этой таблице являются соответствующими
значениями 2 .

6.

Если вероятность p – это означает, что опытные данные
противоречат гипотезе H, состоящей в том, что случайная величина X
имеет представленный выше гипотетический ряд распределения (табл.
33) и гипотезу H необходимо отбросить.
Если вероятность p – это означает, что можно считать
расхождения между статистическим рядом распределения (табл. 32) и
гипотетическим рядом распределения (табл. 33) несущественными и
можно считать выдвинутую гипотезу H правдоподобной, или, по
крайней мере, не противоречащей опытным данным.
Непрерывная случайная величина. В этом случае непрерывную
случайную величину X заменяют дискретной случайной величиной с
возможными значениями ~
x1 , ~
x2 , ..., ~
xi , ..., ~
xr , где ~
xi – середина i-го разряда
(интервала), а pi* – относительная частота попадания случайной
величины X в i-й разряд, и составляют соответствующий статистический
ряд (табл. 34).

7.

Таблица 34
~
x1
~
x2
…
~
xi
…
~
xr
p1*
p2*
…
pi*
…
pr*
Дальнейшие вычисления проводят по процедуре, рассмотренной в
случае дискретной случайной величины.
Пример. Результаты 500 наблюдений над случайной величиной X,
представлены в табл. 35. Пользуясь критерием Пирсона проверить
гипотезу, что случайная величина X распределена по нормальному
закону при условии, что
1) сумма относительных частот равна единице,
2) статистическое среднее равно гипотетическому среднему,
3) статистическая дисперсия равна гипотетической дисперсии.
Уровень значимости 0,1 .

8.

Таблица 35
Разряды 4 3 3 2 2 1 1 0 0 1
n i*
6
25
72
133
120
1 2
2 3
3 4
88
46
10
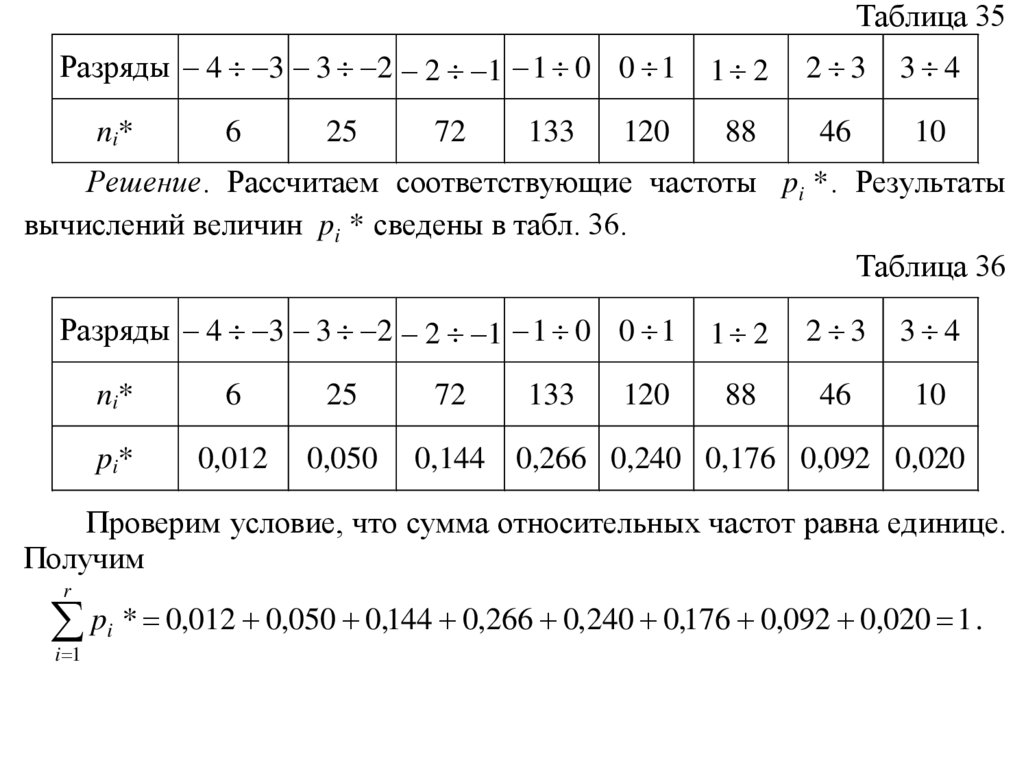
Решение. Рассчитаем соответствующие частоты pi * . Результаты
вычислений величин pi * сведены в табл. 36.
Таблица 36
Разряды 4 3 3 2 2 1 1 0 0 1
133
120
1 2
2 3
3 4
88
46
10
n i*
6
25
72
p i*
0,012
0,050
0,144 0,266 0,240 0,176 0,092 0,020
Проверим условие, что сумма относительных частот равна единице.
Получим
r
pi * 0,012 0,050 0,144 0,266 0,240 0,176 0,092 0,020 1 .
i 1

9.

Для расчета статистического среднего M * X и статистической
дисперсии D * X найдем середину i-го разряда ~x i и припишем этому
значению относительную частоту pi * . Результаты вычислений сведем в
табл. 37.
Таблица 37.
~
xi
3,5
2,5
1,5
p i*
0,012
0,050
0,144 0,266 0,240 0,176 0,092 0,020
0,5
0,5
1,5
2,5
3,5
По данным этой таблице находим:
M * X 3,5 * 0,012 2,5 * 0,05 1,5 * 0,144 0,5 * 0,266
0,5 * 0,240 1,5 * 0,176 2,5 * 0,092 3,5 * 0,020 0,168 ,
2
2
2
M * X 2 3,5 * 0,012 2,5 * 0,05 1,5 * 0,144
2
2
2
2
0,5 * 0,266 0,5 * 0,240 1,5 * 0,176 2,5 * 0,092
3,5 * 0,020 2,126 ,
D * X M * X 2 M * X 2,098 ,
X D X * X D * X 2,098 1,448 .
2

10.

Составим таблицу вероятностей попадания случайной величины X,
распределенной по нормальному закону с параметрами a 0,168 и
1,448 , в соответствующие разряды. Для этого рассчитаем
соответствующие вероятности. Получим
3 0,168
4 0,168
p( 4 3)
0,0126 ,
1,448
1,448
2 0,168
3 0,168
p( 3 2)
0,0522 ,
1,448
1,448
1 0,168
2 0,168
p( 2 1)
0,1422 ,
1,448
1,448
0 0,168
1 0,168
p( 1 0)
0,2433 ,
1,448
1,448
1 0,168
0 0,168
p(0 1)
0,2668 ,
1,448
1,448
2 0,168
1 0,168
p(1 2)
0,1789 ,
1,448
1,448

11.

3 0,168
2 0,168
p(2 3)
0,0770 ,
1,448
1,448
4 0,168
3 0,168
p(3 4)
0,0212 .
1,448
1,448
Результаты вычислений заносим в таблицу 38
Таблица 38.
Разряды 4 3 3 2 2 1 1 0 0 1
pi
1 2
2 3
3 4
0,0126 0,0522 0,1422 0,2433 0,2668 0,1789 0,0770 0,0212
Таблица 36.
Разряды 4 3 3 2 2 1 1 0 0 1
133
120
1 2
2 3
3 4
88
46
10
n i*
6
25
72
p i*
0,012
0,050
0,144 0,266 0,240 0,176 0,092 0,020
При помощи таблиц 36 и 38 вычислим величину 2 :
8
2
i 1
ni * npi 2 3,99 .
npi

12.

Находим число степеней свободы k. В соответствии с изложенным выше,
оно равно разрядов r 8 за вычетом числа 3 наложенных связей:
r
r
r
i 1
i 1
i 1
pi * 1 , xi pi * M X и xi mx * pi * D( X ) . Таким образом,
2
имеем k 8 3 5 . По таблице значений 2 при k 5 и 2 3,99
находим:
Поскольку
расхождения
между
p 0,55 .
p ,
статистическим рядом распределения и гипотетическим рядом
распределения можно считать несущественными и можно считать
выдвинутую гипотезу о нормальности распределения случайной
величины X правдоподобной.