Элементы математической статистики. Глава 2

1.

Глава 2 Элементы математической статистики
§ 1. Генеральная и выборочная совокупности
Генеральной совокупностью называют множество объектов
(элементов) одинаковой природы, которое необходимо проверить на
некоторый количественный или качественный признак.
Выборкой
(выборочной
совокупностью)
называют
часть
(подмножество) объектов генеральной совокупности.
Объемом совокупности называют число объектов совокупности, его
обозначают символом N в случае генеральной совокупности, n – в случае
выборки.
Пример. Генеральной совокупностью является партия из 100000
деталей. Качественным признаком может служить стандартность
деталей, количественным – контролируемый размер деталей. Если для
изучения отобрано 200 деталей, то N 100000 , n 200 .
Если объекты генеральной совокупности различны между собой, то
число различных выборок объема n, извлекаемых из N объектов равно
числу сочетаний из N по n:
N!
.
C Nn
n! N n !

2.

Пример. Генеральная совокупность содержит N 5 объектов A, B, C,
D, E. Тогда существуют десять различных выборок объема n 2 : AB, AC,
AD, AE, BC, BD, BE, CD, CE, DE. Согласно формуле имеем
5! 1 2 3 4 5
C52
10 .
2!3! 1 2 1 2 3
По данным выборки определяют интересующий признак генеральной
совокупности. Если выборка хорошо воспроизводит генеральную
совокупность, то ее называют репрезентативной (представительной).
Выборка будет репрезентативной, если:
1) объем выборки достаточно велик,
2) каждый объект выборки случайно отобран из генеральной совокупности,
3) все объекты генеральной совокупности имеют одинаковую вероятность
попасть в выборку.
Пример. На предприятии работает 20000 сотрудников, средняя заработная
плата сотрудников предприятия равна 15000 рублей в месяц. После опроса
200 сотрудников предприятия получена средняя заработная плата 14900
рублей в месяц. Эти результаты достаточно близки, мы имеем
репрезентативную выборку из 200 объектов, хорошо характеризующую
генеральную совокупность из 20000 объектов по количественному признаку
«средняя заработная плата».

3.

Повторной выборкой называют выборку, при которой извлеченный
из генеральной совокупности объект перед извлечением следующего
объекта возвращается в генеральную совокупность.
Бесповторной выборкой называют выборку, при которой
извлеченный из генеральной совокупности объект перед извлечением
следующего объекта не возвращается в генеральную совокупность.
§ 2. Вариационный ряд и его характеристики
Пусть из генеральной совокупности извлечена выборка объема n,
причем значения x1 , x2 ,.., xi ,... количественного признака X наблюдались
соответственно n1 , n2 ,.., ni ,... раз, n ni .
Вариантами называют наблюдаемые значения xi признака X,
частотами называют соответствующие числа наблюдений ni,
относительными частотами (частостями) называют величины
wi ni n .
Вариационным рядом называют последовательность вариант,
записанную в возрастающем порядке.

4.

Статистическим распределением выборки называют перечень
вариант и соответствующих им частот или относительных частот.
Пример. Задано распределение частот выборки объема n=20:
xi
2
6
9
ni
3
11
6
Написать распределение относительных частот.
3
11
6
Решение.
Имеем
w1
0,15, w2
0,55, w3
0,30 .
20
20
20
Следовательно, искомое распределение имеет вид:
xi
2
6
9
wi
0,15 0,55 0,30
Статистическое распределение выборки задают также в виде
последовательности интервалов и соответствующих им частот. В этом
случае интервальными разностями называют разности x2 x1 , x3 x2 , ...
(они могут быть не равны между собой), частота интервала равна
сумме частот, попавших в данный интервал.

5.

Пример. В таблице приведено интервальное распределение 20
кошек по весу.
Вес кошки 3,0–3,5 3,5–4,0 4,0–4,5 4,5–5,0 5,0–5,5 5,5–6,0
Частота
1
3
7
6
2
1
Размахом вариационного ряда называют разность между
наибольшим и наименьшим значением признака
R xmax xmin .
Модой Mo называют величину признака, которая чаще всего
встречается в вариационном ряде. Если несколько соседних значений
ряда имеют наибольшую частоту, то модой является их среднее
арифметическое. Если все значения вариант встречаются одинаково
часто, то ряд моды не имеет.
Медианой Me называют значение признака, находящегося в
середине вариационного ряда. Если объем выборки n нечетное число, т.е.
n 2l 1, то Me xl . Если объем выборки n четное число, т.е. n 2l , то
Me xl xl 1 2 .

6.

Пример. Найти размах, моду и медиану для вариационного ряда 1,
1, 2, 3, 3, 3, 4, 5, 6, 7.
Решение. Размах вариационного ряда R xmax xmin 7 1 6 .
Наиболее часто (три раза) встречается число 3. Следовательно
M0 3.
Объем выборки n 10 – четное число. Следовательно,
Me x5 x6 2 3 3 2 3 .
§ 3. Теоретическая и эмпирическая функция распределения
Теоретической функцией распределения F(x) называют функцию
распределения генеральной совокупности, определяющую вероятность
события, что количественный признак X будет меньше x, т.е.
F x P X x .
Пусть распределение частот количественного признака X в выборке
объема n известно, nx – число наблюдений, при которых наблюдалось
значение признака X меньшее x. Тогда относительная частота события
X x равна n x n .

7.

Эмпирической функцией распределения
(функцией
F * x
распределения
выборки)
называют
функцию,
определяющую
относительную частоту события X x , т.е.
n
n
F * x x i .
n xi x n
Функция F * x обладает всеми свойствами функции F x :
1) значения функции F * x принадлежат отрезку 0;1 ;
2) F * x – неубывающая функция;
3) если x1 – наименьшая варианта, то F * x 0 при x x1 ; если xk –
наибольшая варианта, то F * x 1 при x x k .
При большом объеме выборки F * x и F x мало отличаются друг
от друга и F * x можно использовать для оценки F x .

8.

Пример. Построить эмпирическую функцию распределения по
распределению выборки:
xi
2
6
10
ni
24
36
60
Решение. Объем выборки n 24 36 60 120 .
Наименьшая варианта x 2 . Следовательно, при x 2 F * x 0 .
Значение X 6 наблюдалось 24 раза. Следовательно, при 2 x 6
F * x 24 120 0,2 .
Значение X 10 наблюдалось 60 раз. Следовательно, при 6 x 10
F * x 60 120 0,5 .
Наибольшая варианта x 10 . Следовательно, при x 10 F * x 1 .
Искомая
эмпирическая
функция F*(x)
распределения имеет вид
1,0
0 при x 2
0,2 при 2 x 6
0,5
F * x
0,5 при 6 x 10
0,2
1 при x 10.
2 6 10 X

9.

§ 4. Полигон и гистограмма частот
Полигоном частот называют ломаную линию, отрезки которой
соединяют точки x1 , n1 , x 2 , n2 , ..., x k , nk .
Полигоном относительных частот называют ломаную линию,
отрезки которой соединяют точки x1 , w1 , x2 , w2 , ..., xk , wk .
Гистограммой частот называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых служат интервалы длиною h,
а высоты равны n i h , ni – сумма частот вариант, попавших в i-й
интервал. Площадь i-го прямоугольника равна ni h h ni , площадь
гистограммы частот равна объему выборки n.
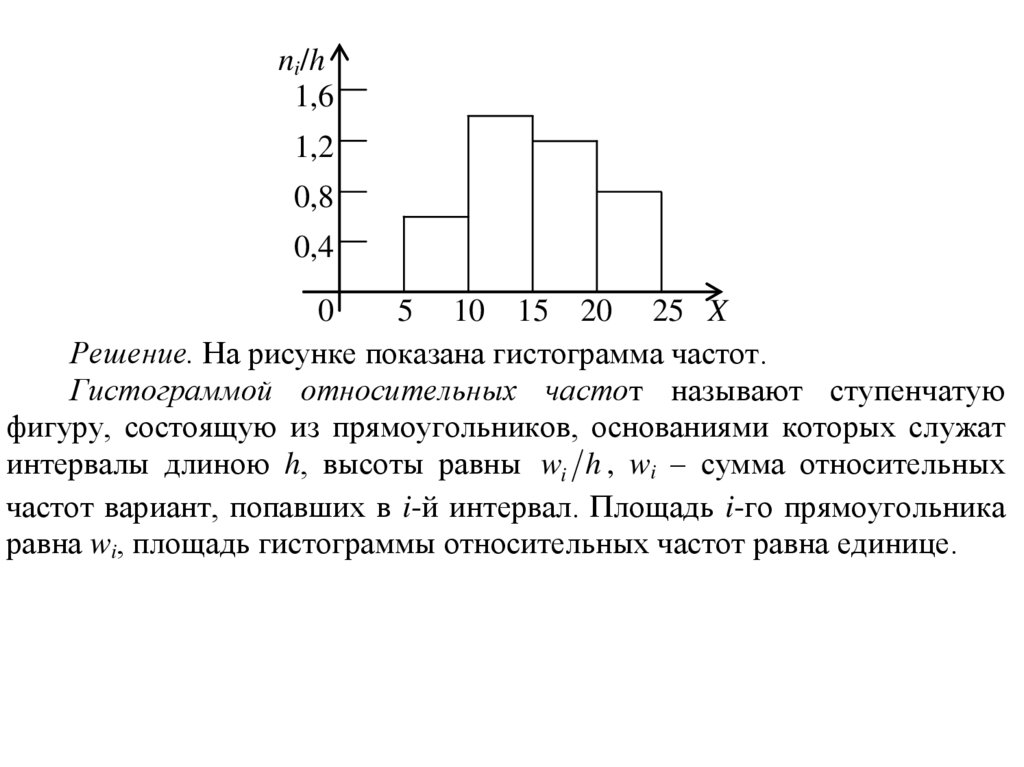
Пример. Построить гистограмму частот распределения объема
n 20 , приведенного в таблице.
Частичный интервал
Сумма частот
Плотность частоты
длиной h=5
частичного интервала
ni/h
ni
5–10
3
0,6
10–15
7
1,4
15–20
6
1,2
20–25
4
0,8

10.

ni/h
1,6
1,2
0,8
0,4
0
5 10 15 20 25 X
Решение. На рисунке показана гистограмма частот.
Гистограммой относительных частот называют ступенчатую
фигуру, состоящую из прямоугольников, основаниями которых служат
интервалы длиною h, высоты равны wi h , wi – сумма относительных
частот вариант, попавших в i-й интервал. Площадь i-го прямоугольника
равна wi, площадь гистограммы относительных частот равна единице.

11.

§ 5. Основные характеристики генеральной и выборочной
совокупности
Пусть значения x1 , x2 , ..., xi ,..., xk количественного признака X в
генеральной совокупности объема N имеют соответственно частоты
k
N1 , N 2 , ..., N i ,..., N k , N i N .
i 1
Генеральным средним xг называют среднее арифметическое
значений признака X в генеральной совокупности
x1 N1 x2 N 2 ... xi N i ... xk N k 1 k
xг
xi N i .
N
N i 1
Значение признака X генеральной совокупности можно рассматривать
как дискретную случайную величину, которая может принимать
различные
значения xi с
вероятностями
Тогда
pi N i N .
математическое ожидание случайной величины X равно
k
1 k
M X x i p i xi N i x г .
N i 1
i 1

12.

Генеральной дисперсией Dг называют среднее арифметическое
квадратов отклонений значений признака X в генеральной совокупности
от генерального среднего xг
k
N i xi xг
Dг i 1
2
N
k
i 1
2
N i xi2 2 xi xг xг2
N
k
i 1
k
N i xi2
N
N i xi
2 xг i 1
N
k
Ni
2
N x 2x x x x
xг
i 1
2
2
г
2
г
2
2
г
Генеральным средним квадратическим отклонением г называют
квадратный корень из генеральной дисперсии Dг: г Dг .
Пусть значения x1 , x2 , ..., xi ,..., xl признака X выборки объема n
l
имеют соответственно частоты n1 , n2 , ..., ni ,..., nl , ni n .
i 1
Выборочным средним xв называют среднее арифметическое
значений признака X в выборочной совокупности
x1n1 x2 n2 ... xi ni ... xl nl 1 l
xв
xi ni .
n
n i 1

13.

Выборочной дисперсией Dв называют среднее арифметическое
квадратов отклонений значений признака X в выборочной совокупности
от выборочного среднего xв
l
N i xi x в
Dв i 1
2
N
l
i 1
N x
2
2 2
N i x i 2 xi x в x в
N
l
i 1
2
i i
N
l
N i xi
2 xв i 1
N
l
Ni
2
N x 2x x x x
xв
i 1
2
2
в
2
в
2
2
в
Выборочным средним квадратическим отклонением в называют
квадратный корень из выборочной дисперсии
в Dв .