Математический аппарат, применяемый в автоматизированных системах лабораторных экспериментов

1.

2.

Математический аппарат, применямый в
автоматизированных системах лабораторных
экспериментов
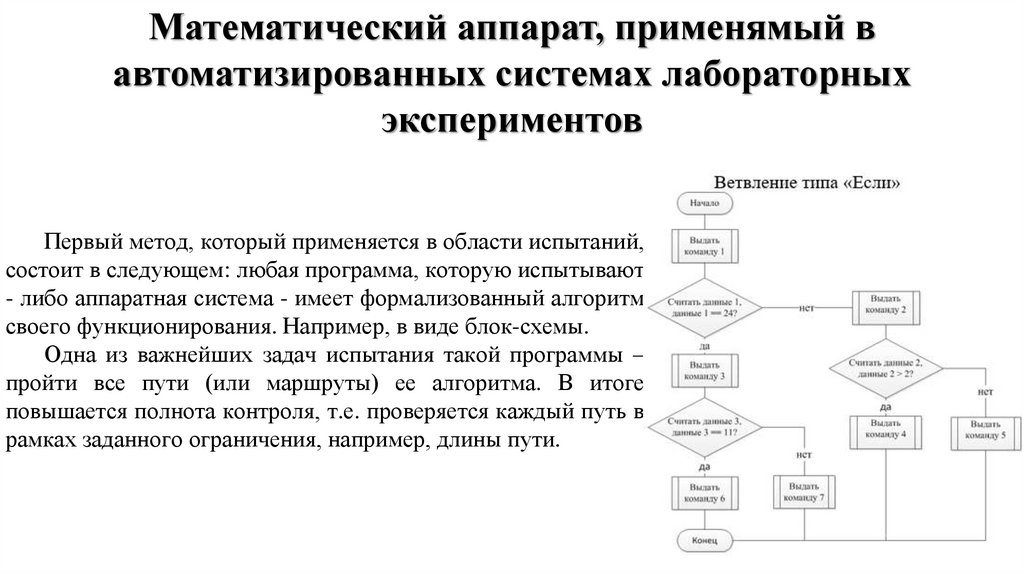
Первый метод, который применяется в области испытаний,
состоит в следующем: любая программа, которую испытывают
- либо аппаратная система - имеет формализованный алгоритм
своего функционирования. Например, в виде блок-схемы.
Одна из важнейших задач испытания такой программы –
пройти все пути (или маршруты) ее алгоритма. В итоге
повышается полнота контроля, т.е. проверяется каждый путь в
рамках заданного ограничения, например, длины пути.

3.

Математический аппарат, применямый в
автоматизированных системах лабораторных
экспериментов
При вычислении всех путей в ручном режиме нельзя исключать человеческий фактор. Если
упустить какой-либо путь, возможны сбои системы при ее штатной эксплуатации. Поэтому данную
проблему необходимо решать путем автоматизации процесса вычисления путей.

4.

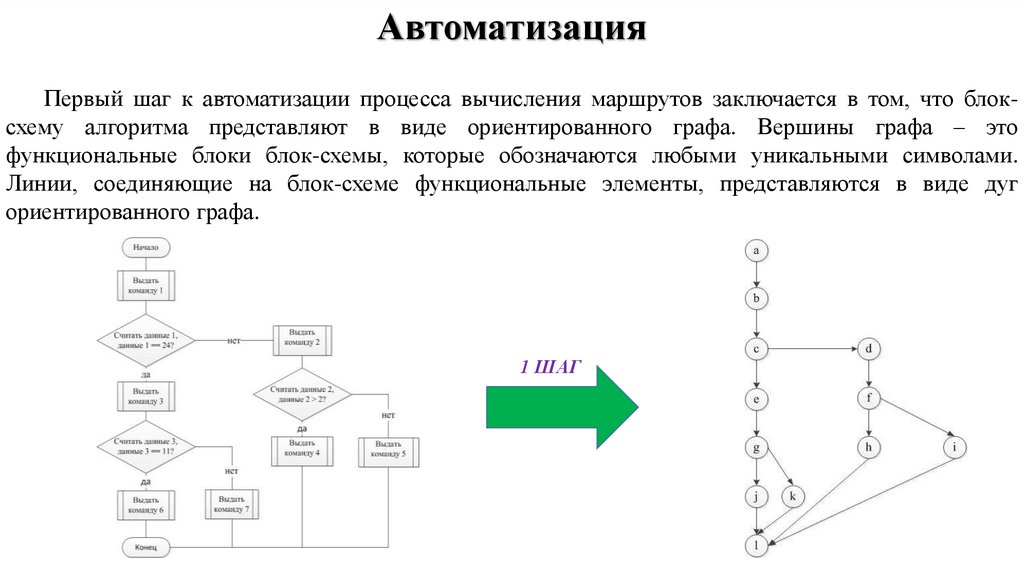
Автоматизация
Первый шаг к автоматизации процесса вычисления маршрутов заключается в том, что блоксхему алгоритма представляют в виде ориентированного графа. Вершины графа – это
функциональные блоки блок-схемы, которые обозначаются любыми уникальными символами.
Линии, соединяющие на блок-схеме функциональные элементы, представляются в виде дуг
ориентированного графа.
1 ШАГ

5.

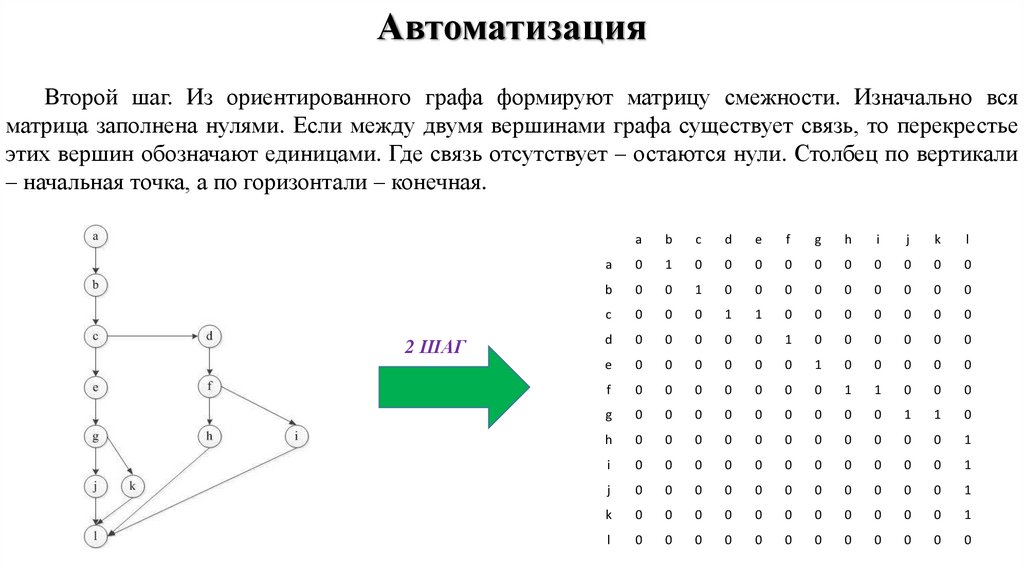
Автоматизация
Второй шаг. Из ориентированного графа формируют матрицу смежности. Изначально вся
матрица заполнена нулями. Если между двумя вершинами графа существует связь, то перекрестье
этих вершин обозначают единицами. Где связь отсутствует – остаются нули. Столбец по вертикали
– начальная точка, а по горизонтали – конечная.
2 ШАГ
a
b
c
d
e
f
g
h
i
j
k
l
a
0
1
0
0
0
0
0
0
0
0
0
0
b
0
0
1
0
0
0
0
0
0
0
0
0
c
0
0
0
1
1
0
0
0
0
0
0
0
d
0
0
0
0
0
1
0
0
0
0
0
0
e
0
0
0
0
0
0
1
0
0
0
0
0
f
0
0
0
0
0
0
0
1
1
0
0
0
g
0
0
0
0
0
0
0
0
0
1
1
0
h
0
0
0
0
0
0
0
0
0
0
0
1
i
0
0
0
0
0
0
0
0
0
0
0
1
j
0
0
0
0
0
0
0
0
0
0
0
1
k
0
0
0
0
0
0
0
0
0
0
0
1
l
0
0
0
0
0
0
0
0
0
0
0
0

6.

Автоматизация
Третий шаг. В созданной матрице смежности производят замену символа «1» на ранее принятый
уникальный символ. Например, существует маршрут из «а» в «b», следовательно единицу заменяют
на символ «b». Таким образом, единицу заменяют на символ конечной вершины в существующей
связи. В итоге получают матрицу смежности с уникальными символами.
a
b
c
d
e
f
g
h
i
j
k
l
a
0
b
0
0
0
0
0
0
0
0
0
0
0
b
0
0
c
0
0
0
0
0
0
0
0
0
0
0
c
0
0
0
d
e
0
0
0
0
0
0
0
0
0
0
d
0
0
0
0
0
f
0
0
0
0
0
0
0
0
0
0
e
0
0
0
0
0
0
g
0
0
0
0
0
1
1
0
0
0
f
0
0
0
0
0
0
0
h
i
0
0
0
0
0
0
1
1
0
g
0
0
0
0
0
0
0
0
0
j
k
0
0
0
0
0
0
0
1
h
0
0
0
0
0
0
0
0
0
0
0
l
0
0
0
0
0
0
0
1
i
0
0
0
0
0
0
0
0
0
0
0
l
0
0
0
0
0
0
0
0
1
j
0
0
0
0
0
0
0
0
0
0
0
l
0
0
0
0
0
0
0
0
0
1
k
0
0
0
0
0
0
0
0
0
0
0
l
0
0
0
0
0
0
0
0
0
0
l
0
0
0
0
0
0
0
0
0
0
0
0
a
b
c
d
e
f
g
h
i
j
k
l
a
0
1
0
0
0
0
0
0
0
0
0
0
b
0
0
1
0
0
0
0
0
0
0
0
c
0
0
0
1
1
0
0
0
0
0
d
0
0
0
0
0
1
0
0
0
e
0
0
0
0
0
0
1
0
f
0
0
0
0
0
0
0
g
0
0
0
0
0
0
h
0
0
0
0
0
i
0
0
0
0
j
0
0
0
k
0
0
l
0
0
3 ШАГ

7.

Автоматизация
Четвертый шаг. Рассчитать все пути определенной длины, которые присутствуют в графе. Для этого
возводят матрицу в степень длины искомых путей. В данном примере длина искомых путей равна 2, т.е.
матрица возведена в квадрат.
Маршрут из «a» в «c», проложен через вершину «b». Символ «+» означает, что существует 2 и более
путей длинной 2. Например, из вершины «f» в вершину «l» можно добраться двумя путями, через вершину
«h» или «i».
a
b
c
d
e
f
g
h
i
j
k
l
a
0
0
b
0
0
0
0
0
0
0
0
0
0
b
0
0
0
c
c
0
0
0
0
0
0
0
0
0
c
0
0
0
0
0
d
e
0
0
0
0
0
0
0
0
d
0
0
0
0
0
0
0
f
f
0
0
0
0
0
0
0
e
0
0
0
0
0
0
0
0
0
g
g
0
h
i
0
0
0
f
0
0
0
0
0
0
0
0
0
0
0
h+i
0
0
0
j
k
0
g
0
0
0
0
0
0
0
0
0
0
0
j+k
0
0
0
0
0
0
l
h
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
l
i
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
l
j
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
l
k
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
l
0
0
0
0
0
0
0
0
0
0
0
0
a
b
c
d
e
f
g
h
i
j
k
l
a
0
b
0
0
0
0
0
0
0
0
0
0
b
0
0
c
0
0
0
0
0
0
0
0
c
0
0
0
d
e
0
0
0
0
0
d
0
0
0
0
0
f
0
0
0
e
0
0
0
0
0
0
g
0
f
0
0
0
0
0
0
0
g
0
0
0
0
0
0
h
0
0
0
0
0
i
0
0
0
0
j
0
0
0
k
0
0
l
0
0
4 ШАГ
P2 =

8.

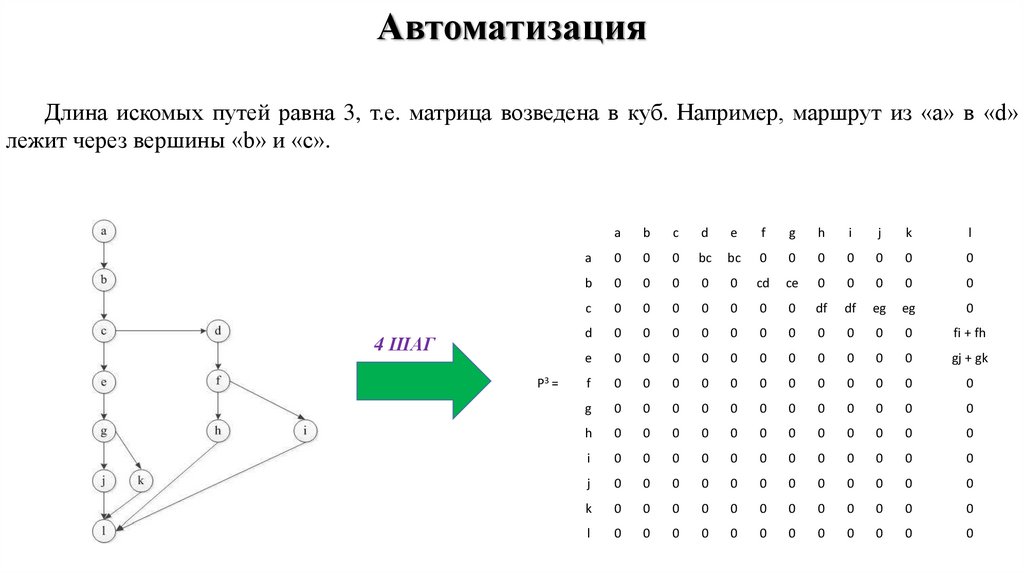
Автоматизация
Длина искомых путей равна 3, т.е. матрица возведена в куб. Например, маршрут из «a» в «d»
лежит через вершины «b» и «c».
4 ШАГ
P3 =
a
b
c
d
e
f
g
h
i
j
k
l
a
0
0
0
bc
bc
0
0
0
0
0
0
0
b
0
0
0
0
0
cd
ce
0
0
0
0
0
c
0
0
0
0
0
0
0
df
df
eg
eg
0
d
0
0
0
0
0
0
0
0
0
0
0
fi + fh
e
0
0
0
0
0
0
0
0
0
0
0
gj + gk
f
0
0
0
0
0
0
0
0
0
0
0
0
g
0
0
0
0
0
0
0
0
0
0
0
0
h
0
0
0
0
0
0
0
0
0
0
0
0
i
0
0
0
0
0
0
0
0
0
0
0
0
j
0
0
0
0
0
0
0
0
0
0
0
0
k
0
0
0
0
0
0
0
0
0
0
0
0
l
0
0
0
0
0
0
0
0
0
0
0
0

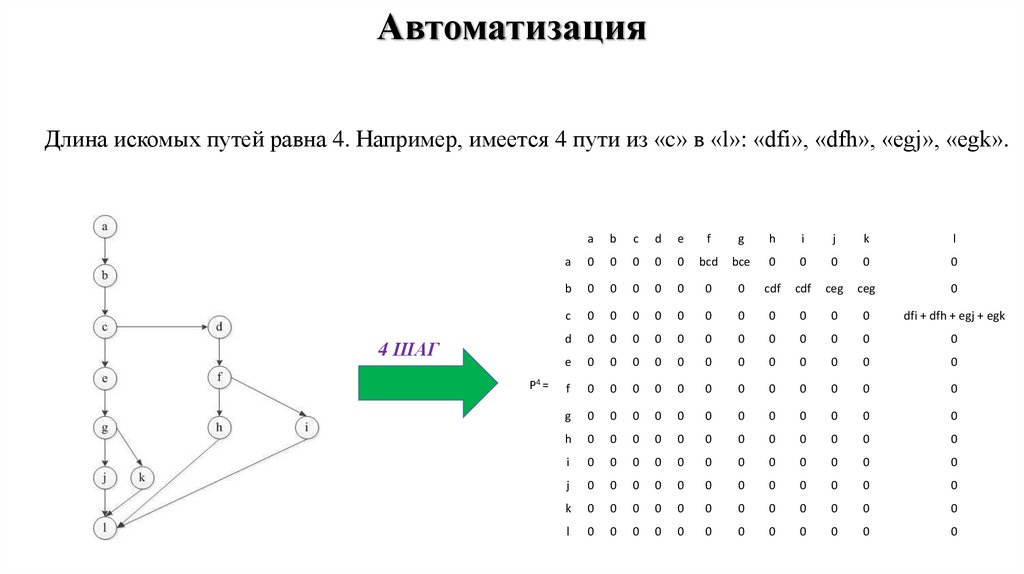
9.

Автоматизация
Длина искомых путей равна 4. Например, имеется 4 пути из «c» в «l»: «dfi», «dfh», «egj», «egk».
4 ШАГ
P4 =
a
b
c
d
e
f
g
h
i
j
k
l
a
0
0
0
0
0
bcd
bce
0
0
0
0
0
b
0
0
0
0
0
0
0
cdf
cdf
ceg
ceg
0
c
0
0
0
0
0
0
0
0
0
0
0
dfi + dfh + egj + egk
d
0
0
0
0
0
0
0
0
0
0
0
0
e
0
0
0
0
0
0
0
0
0
0
0
0
f
0
0
0
0
0
0
0
0
0
0
0
0
g
0
0
0
0
0
0
0
0
0
0
0
0
h
0
0
0
0
0
0
0
0
0
0
0
0
i
0
0
0
0
0
0
0
0
0
0
0
0
j
0
0
0
0
0
0
0
0
0
0
0
0
k
0
0
0
0
0
0
0
0
0
0
0
0
l
0
0
0
0
0
0
0
0
0
0
0
0

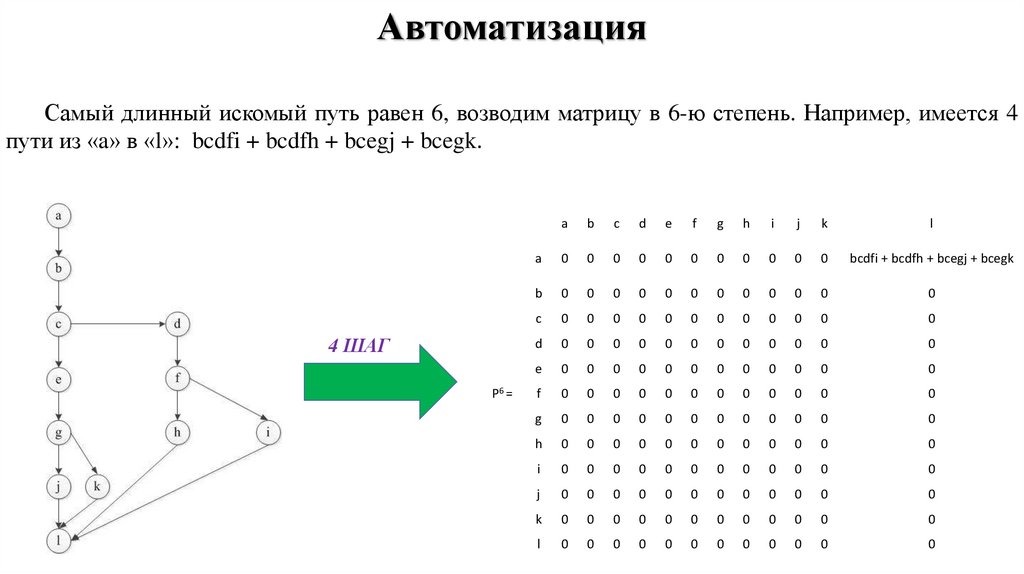
10.

Автоматизация
Самый длинный искомый путь равен 6, возводим матрицу в 6-ю степень. Например, имеется 4
пути из «a» в «l»: bcdfi + bcdfh + bcegj + bcegk.
4 ШАГ
P6 =
a
b
c
d
e
f
g
h
i
j
k
l
a
0
0
0
0
0
0
0
0
0
0
0
bcdfi + bcdfh + bcegj + bcegk
b
0
0
0
0
0
0
0
0
0
0
0
0
c
0
0
0
0
0
0
0
0
0
0
0
0
d
0
0
0
0
0
0
0
0
0
0
0
0
e
0
0
0
0
0
0
0
0
0
0
0
0
f
0
0
0
0
0
0
0
0
0
0
0
0
g
0
0
0
0
0
0
0
0
0
0
0
0
h
0
0
0
0
0
0
0
0
0
0
0
0
i
0
0
0
0
0
0
0
0
0
0
0
0
j
0
0
0
0
0
0
0
0
0
0
0
0
k
0
0
0
0
0
0
0
0
0
0
0
0
l
0
0
0
0
0
0
0
0
0
0
0
0

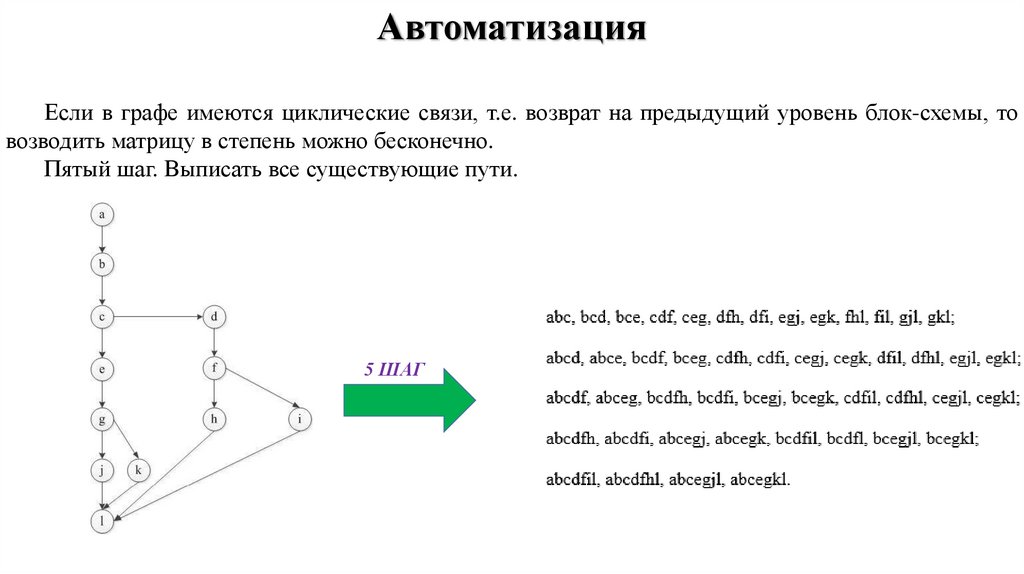
11.

Автоматизация
Если в графе имеются циклические связи, т.е. возврат на предыдущий уровень блок-схемы, то
возводить матрицу в степень можно бесконечно.
Пятый шаг. Выписать все существующие пути.
5 ШАГ

12.

Автоматизация
Шаг шестой. Созданный математический аппарат реализуют в
виде программы ЭВМ. Изображена программа
в среде
операторского уровня National Instruments TestStand. Реализован
алгоритм, блок-схема которого приведена ранее. Каждая строка
программы соответствует функциональному блоку блок-схемы.
В каждой вершине-команде имеются технологические данные,
которые содержат уникальную вершину, соответствующую стоке
программы, которая активирует очередную уникальную вершину.
Данные об идентификаторе уникальной вершины, активированной
каждым конкретным шагом, записываются в протокол испытаний.
Таким образом, по окончанию испытаний сформированный
протокол содержит все пройденные в ходе испытаний пути.
Данные из протокола сравниваются с ранее рассчитанным
перечнем путей, имеющихся в ориентированном графе,
составленном на основе блок-схемы алгоритма. Несовпадение
данных свидетельствует о том, что полнота контроля проведенных
испытаний может быть увеличена.
6 ШАГ

13.

Анализ частотных составляющих
Для анализа частотных составляющих сигнала применяют функцию преобразование Фурье, которая
преобразует данные об амплитуде и частоте сигнала в спектральный вид.
Приведен пример быстрого преобразования Фурье. На графике Ch02 наблюдаем исходный сигнал в виде
амплитудно-частотного представления. На графике Ch0 наблюдаем сигнал с Ch02 в спектральном
представлении. Из кодового описания видно, что получают исходный сигнал в виде массива дробных
значений амплитуды. Далее этот массив подают на вход функции FFT (Fast Fourier transform), результат
которой передают на вход Complex To Re/Im. Функция FFT To Spectrum принимает на вход результат функции
FFT в виде комплексного числа, далее функция Complex To Re/Im разделяет комплексное число на
действительную и мнимую часть и передает их в функцию FFT To Spectrum, которая вычисляет
окончательный результат.

14.

Математический аппарат
Палитра Mathematics содержит стандартные функции по работе с
числами. Также на палитре есть группа Elementary, которая содержит
тригонометрические, гиперболические, экспоненциальные функции,
функции дискретной математики и т.д. Очень много функций по
математической обработке сигналов.

15.

Математический аппарат
Палитра Signal Processing, как и подпалитра Filters, в основе имеют
математический аппарат. Например, функция «фильтра Чебышева».