Геометрические векторы

1.

1. Геометрические векторы:
основные понятия, линейные операции над
векторами и их свойства.
Вектор — это направленный прямолинейный отрезок, т. е. отрезок,
имеющий определенную длину и определенное направление. Если А Сумму двух векторов можно построить по правилу параллелограмма и
начало вектора, а В его конец, то вектор обозначается символом АВ или а. треугольника.
Вектор ВА называется противоположным вектору АВ.
Под разностью векторов а и б понимается вектор с = а б такой, что
Вектор, длина которого равна единице, называется единичным вектором и в+с=а
обозначается через е.
Произведением вектора а на число- вектор Ха, который имеет длину |Х|
Векторы а и б называются коллинеарными, если они лежат на одной
|а|,
прямой
коллинеарен вектору а, имеет направление вектора а, если Х > 0 и
или на параллельных прямых.
противоположное направление, если Х <0.
Два вектора а и б называются равными (а = b), если они коллинеарные,
Свойства умножения:
одинаково направлены и имеют одинаковые длины.
1) если в = Ха, то в||а.
Компланарные векторы - векторы лежат в одной плоскости, среди трех
2) а =|а|*а0 , каждый вектор равен произведению его модуля на орт.
векторов хотя бы один нулевой или два коллинеарные.
Общие свойства линейной комбинации:
Линейные операции над векторами - операции сложения и вычитания и
1) а+в=в+а 3) Х1*(Х2*а)=Х1Х2а 5) Х*(а+в)=Ха+Хв
умножение векторы на число.
2) (а+в)+с=а+(в+с) 4) (Х1+Х2)*а=Х1а+Х2а
Пусть а и б два произвольных вектора. Возьмем произвольную точку О и
построим вектор ОА = а. От точки А отложим вектор АВ = 6. Вектор ОВ,
соединяющий начало первого вектора с концом второго, называется суммой
векторов а и б.

2.

2. Линейная зависимость и независимость векторов.
Базис, разложение
вектора по базису.
Линейно зависимые векторы – векторы, векторного пространства R, если
одновременно существуют такие числа , не равные нулю. То есть:
1a1
2a2 … 0.
Линейно независимые, если не нашлось таких чисел.
Если один из векторов выражается линейно через остальные, то все эти
векторы в совокупности линейно зависимы.
Если среди векторов а, имеется нулевой вектор, то эти векторы линейно
зависимы. Если часть векторов а1, а2, …, является линейно зависимыми, то и
все эти векторы – линейно зависимые.
Базисом пространства - систему векторов в которой все остальные векторы
пространства можно представить в виде линейной комбинации векторов,
входящих в базис.
Базис, как правило, проверяют на плоскости или в пространстве, а для этого
нужно найти определитель матрицы второго, третьего порядка составленный
из координат векторов.
Определитель не нулю, следовательно векторы a1, a2 является базисом на
плоскости.
Разложение вектора по базису — это способ выразить данный вектор через
линейную комбинацию базисных векторов.
Например, если вектор b={8;1}, а базисные векторы p ={1;2} и q ={3;1}, то
разложение вектора по базису можно найти из векторного уравнения:
xp +yq =b
Любой вектор из пространства R может быть представлен в виде линейной
комбинации векторов базиса R. Коэффициенты линейной комбинации координатами вектора в данном базисе, а определяются единственным
образом.

3.

3.Проекция вектора, свойства проекций.

4.

4. Разложение вектора по координатным осям

5.

5. Действия над векторами, заданными проекциями. Координаты точки, координаты вектора

6.

6. Скалярное произведение векторов и его свойства.
Выражение
скалярного произведения через координаты.

7.

8.

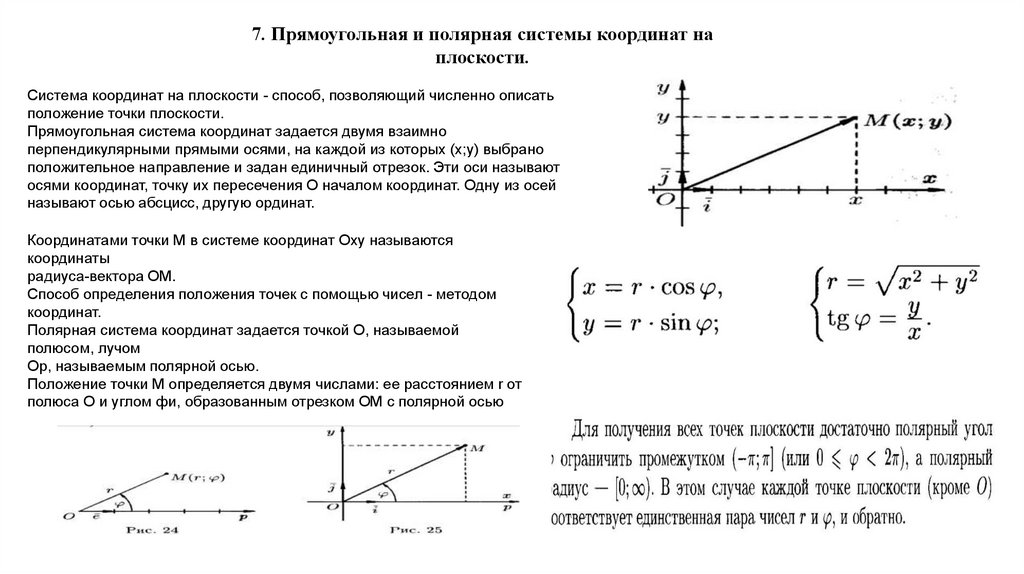
7. Прямоугольная и полярная системы координат на
плоскости.
Система координат на плоскости - способ, позволяющий численно описать
положение точки плоскости.
Прямоугольная система координат задается двумя взаимно
перпендикулярными прямыми осями, на каждой из которых (x;y) выбрано
положительное направление и задан единичный отрезок. Эти оси называют
осями координат, точку их пересечения О началом координат. Одну из осей
называют осью абсцисс, другую ординат.
Координатами точки М в системе координат Оху называются
координаты
радиуса-вектора ОМ.
Способ определения положения точек с помощью чисел - методом
координат.
Полярная система координат задается точкой О, называемой
полюсом, лучом
Ор, называемым полярной осью.
Положение точки М определяется двумя числами: ее расстоянием r от
полюса О и углом фи, образованным отрезком ОМ с полярной осью

9.

8 Основные приложения метода координат на
плоскости: расстояние
между двумя точками, деление отрезка в данном
отношении.

10.

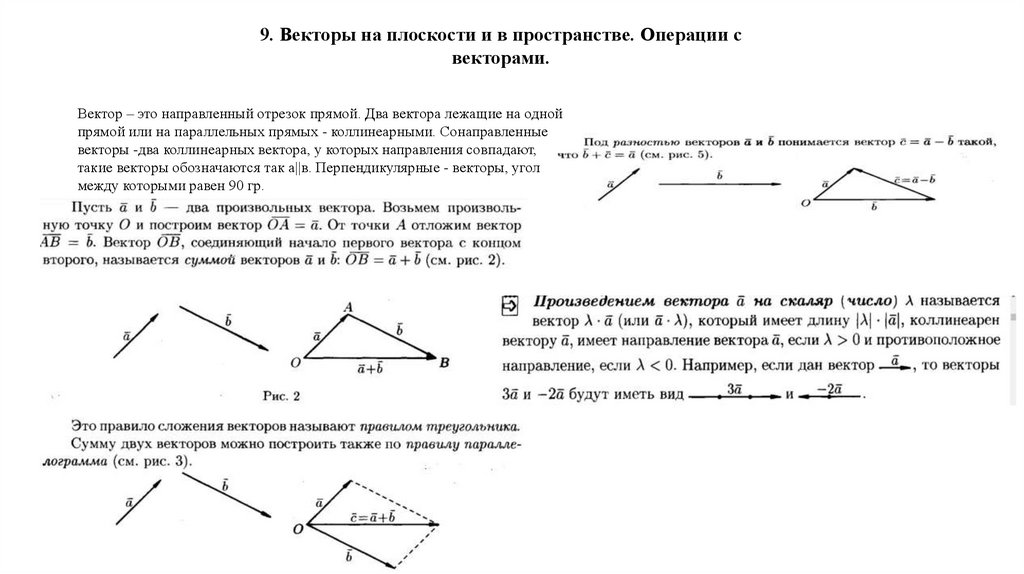
9. Векторы на плоскости и в пространстве. Операции с
векторами.
Вектор – это направленный отрезок прямой. Два вектора лежащие на одной
прямой или на параллельных прямых - коллинеарными. Сонаправленные
векторы -два коллинеарных вектора, у которых направления совпадают,
такие векторы обозначаются так a||в. Перпендикулярные - векторы, угол
между которыми равен 90 гр.

11.

10. Уравнения прямой на плоскости, содержащие
угловой коэффициент.

12.

11. Уравнение прямой, проходящей через две точки.
Уравнение прямой в
отрезках. Общее уравнение прямой на плоскости

13.

12. Основные задачи на прямую линию на плоскости:
угол между
прямыми, условия параллельности и
перпендикулярности прямых, точка пересечения
прямых, расстояние от точки до прямой

14.

13. Уравнения плоскости
B пространстве:
уравнение плоскости,
проходящей через данную точку перпендикулярно
данному вектору, общее уравнение плоскости.

15.

14. Уравнения плоскости в пространстве:
уравнение плоскости,
проходящей через три данные точки, уравнение
плоскости в отрезках