Равновесие пространственной системы сил

1.

Равновесие пространственной
системы сил
• Пространственная система сил – система сил, линии
действия которых расположены произвольным образом в
пространстве.
Для равновесия системы сил, приложенных к твердому
телу необходимо и достаточно, чтобы главный вектор этой
системы сил ее главный момент относительно
произвольно выбранного центра были равны нулю

2.

Эти векторные равенства, на основании
выражений проекции главного вектора и проекции
главного момента на координатные оси –
эквивалентны следующим шести скалярным
уравнениям:

3.

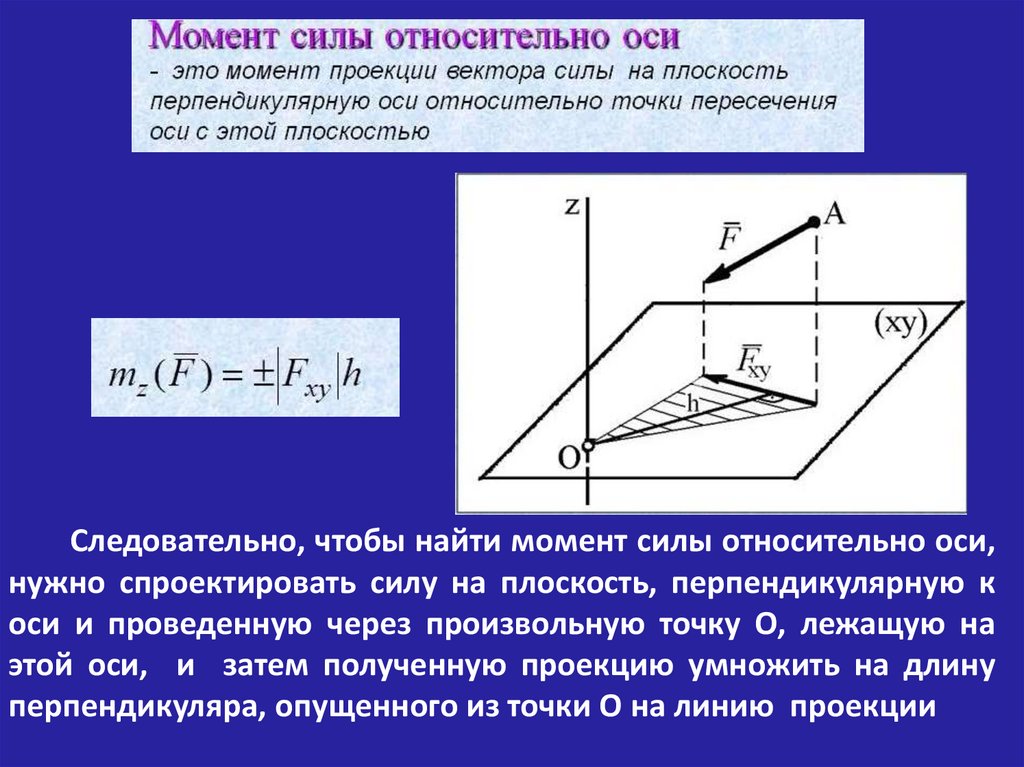
Следовательно, чтобы найти момент силы относительно оси,
нужно спроектировать силу на плоскость, перпендикулярную к
оси и проведенную через произвольную точку О, лежащую на
этой оси, и затем полученную проекцию умножить на длину
перпендикуляра, опущенного из точки О на линию проекции

4.

Знак момента силы относительно данной оси выбирается
следующим образом:
если наблюдатель, смотрящий с положительного конца данной оси
видит проекцию силы направленной по отношению к точке О
против часовой стрелки, то момент силы относительно этой оси
считается положительным, в противном случае – отрицательным.
Момент силы относительно оси равен нулю, если проекция силы
или плечо равны нулю, т. е. когда сила параллельна оси, либо когда
линия действия этой силы пересекает данную ось.

5.

Определим моменты сил и относительно осей
Решение. Моменты силы находятся просто:
Mx( )=
;
My( )=0;
Mz( )=
.
Моменты сил и - посложнее.
В тех случаях, когда вектор силы направлен под углом к осям, полезно разложить
вектор силы на составляющие параллельные осям и, затем, находить сумму моментов
этих составляющих.
Так моменты силы :
И силы :
(линия действия силы
пересекает ось z).

6.

5.3. Условия равновесия
пространственной системы сил
С механической точки зрения первые три
уравнения устанавливают отсутствие
поступательного, а последние три - углового
перемещения тела.
F 0
F 0
F 0
m ( F ) 0
m ( F ) 0
m ( F ) 0
kx
n
ky
В случае ССС
условия равновесия будут представлены
системой первых трех уравнений.
В случае системы параллельных сил
система будет состоять также из трех
уравнений: из одного уравнения суммы
проекций сил на ту ось, параллельно которой
ориентированы силы системы, и двух
уравнений моментов относительно осей,
непараллельных линиям действия сил системы
n
kz
n
x
k
y
k
z
k
n
n
n

7.

5. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
5.1. Момент силы относительно
центра как вектор
момент силы относительно
центра изображается вектором
Мо, приложенным к центру О и
направленным нормально
плоскости, задаваемой вектором
силы F и центром O, в ту сторону,
откуда видится вращение вектора
силы относительно центра
против хода часовой стрелки
mo F r F
z
mo F
B
A F
r
O
h
x
r F r F sin r ,̂ F F h
r sin r ,̂ F r sin h
y

8.

5.2. Моменты силы относительно осей
mo F r F x
j
k
y
z
Fx
Fy
Fz
i
i Fz y Fy z j Fx z Fz x k Fy x Fx y
mo F тx F т y F тz F
i тx F j т y F k тz F
тx F Fz y Fy z
Fx z Fz x
тy F
т F F x F y
y
x
z